若干本原有向图类其广义本原r-指数的界

黄宇飞 ，柳柏濂

(1. 广州民航职业技术学院，广州510403;2. 华南师范大学数学科学学院，广州510631)

记n 阶(0，1)矩阵集为Bn.对于A=(aij) Bn，其可以和一个具有n个顶点的有向图D =(V，E)建立一一对应关系，其中V ={v1，v2，…，vn}是标号顶点集，E 是弧集，且这里1≤i，j≤n.称A(或记为A(D))为有向图D 的邻接矩阵，把D(或记为D(A))叫做矩阵A 的伴随有向图.

记所有元素都是“1”的n 阶矩阵为Jn. 一个矩阵A Bn称为本原的，如果存在正整数k 使得Ak=Jn;等价地，一个有向图D =(V，E)是本原的，如果存在正整数k 使得任意两点u，v V(u 和v 可以表示同一点)，在D 中有从点u 到点v 长为k 的途径.我们把n 阶本原矩阵集(或本原有向图集)记为Pn.

对于一个有向图D=(V，E)及点子集X⊆V，以Rt(X)(又称可达集)表示从点子集X 中的任意顶点出发，通过长为t 的途径所能到达的所有点的集合，其中t 为非负整数. 设D =(V，E)是一个本原有向图，容易验证:R0(X)=X，Ri(X)=Ri-j(Rj(X))，其中X⊆V，且i 和j 是满足i≥j 的非负整数.

在有限马尔科夫链理论中，转移概率的遍历性及遍历指数的问题，与本原矩阵的局部性质有着自然的联系［1-2］.根据理论和实践的需要，基于非记忆通信系统的数学模型［3］，Huang 和Liu［4］于2011年提出了4 类广义本原r-指数的概念:设n，k，r 是满足1≤k，r≤n 的正整数，则

(1)本原矩阵A Pn的k 点r-指数pr(A，k)是A 的最小幂指数，使得在这个幂中存在k ×n 阶子矩阵每行均有r个“1”元;等价地，本原有向图D Pn的k 点r-指数pr(D，k)是最小的非负整数p，使得存在由k个点构成的子集X⊆V(D)，对于每一个顶点x X 都有|Rp({x})|≥r.

(2)本原矩阵A Pn的k 点r-同位指数sr(A，k)是A 的最小幂指数，使得在这个幂中存在k×r 阶全“1”子矩阵;等价地，本原有向图D Pn的k 点r-同位指数sr(D，k)是最小的非负整数p，使得存在由k个点构成的子集X⊆V(D)，及某r个点v1，…，vrV(D)，其满足∀x X 都有Rp({x})⊇{v1，…，vr}.

(3)本原矩阵A Pn的第k 重下r-指数fr(A，k)是A 的最小幂指数，使得在这个幂中存在k×r 阶无零列子矩阵;等价地，本原有向图D Pn的第k重下r-指数fr(D，k)是最小的非负整数p，使得存在k 点子集X⊆V(D)满足|Rp(X)|≥r.

(4)本原矩阵A Pn的第k 重上r-指数Fr(A，k)是A 的最小幂指数，使得在这个幂中任意k ×n阶子矩阵至多有n -r 列全零列;等价地，本原有向图D Pn的第k 重上r-指数Fr(D，k)是最小的非负整数p，使得任意k个点构成的子集X⊆V(D)均满足|Rp(X)|≥r.

广义本原r-指数是著名的本原指数和广义本原指数［5-6］的进一步拓广，其对本原矩阵幂序列中的行和列进行了更精细的刻画.在文献［3］中，关于一般的n 阶本原矩阵(有向图)的4 类广义本原r-指数的上界问题得到了初步的研究. 本文将继续探讨若干特殊的本原矩阵(有向图)类(如:w-不可分矩阵、w-几乎可分矩阵、完全不可分矩阵、几乎可分矩阵、含多圈结构的本原有向图、含交圈结构的本原有向图、微对称本原矩阵和对称本原矩阵等)其广义本原r-指数的上界问题.

1 不可分矩阵的广义本原r-指数

设w 是满足-n ＜w ＜n 的整数.如果A Bn不含k×l 阶零子矩阵，其中1≤k，l≤n 且k +l =n -w+1，则称A 为w-不可分方阵［7］，亦称其伴随有向图D=D(A)是w-不可分的. 记n 阶w-不可分方阵(有向图)之集为Bn，w.易见，w-不可分方阵有如下的图论刻画［7-9］:A Bn，w当且仅当D(A)中任一k(1≤k≤n)点子集X⊆V(D(A))都有|R1(X)|≥min{n，k+w}.对于A Bn，w，若将其任一非零元换成零元后所得矩阵不再是w-不可分的，则称A 为w-几乎可分方阵［7］，同样把其伴随有向图D =D(A)称作w-几乎可分的.又记n 阶w-几乎可分方阵(有向图)之集为NDn，w.特别地，把1-不可分方阵(有向图)和1-几乎可分方阵(有向图)又分别称为完全不可分方阵(有向图)和几乎可分方阵(有向图)，且记Bn，1=Fn，NDn，1=NDn.

另外，对于整数w1(-n+1 ＜w1＜n)和w2(1≤w2＜n)，w1-不可分方阵必然是(w1-1)-不可分方阵，从而w2-不可分方阵必然是完全不可分方阵，故也是本原方阵［7］，即Bn，w1⊆Bn，w1-1，Bn，w2⊆Fn⊆Pn.下面将分别研究w2-不可分矩阵和w2-几乎可分矩阵其k 点r-指数和第k 重上r-指数的上界.

在本节的余下部分，默认假设n，k，r，w 是满足1≤k，r≤n 且1≤w ＜n 的正整数.为方便起见，采用图论的语言来阐述主要结论.

1.1 k 点r-指数

定理1 设D Bn，w(或D NDn，w)，其中1≤w＜n，则pr(D，k)≤「(r-1)/w⏋.

证明 若D Bn，w(1≤w ＜n)，根据其图论意义可知:任一k (1≤k≤n)点子集X⊆V(D)都有|R1(X)|≥min{n，k+w}，从而对于∀v V(D)，有

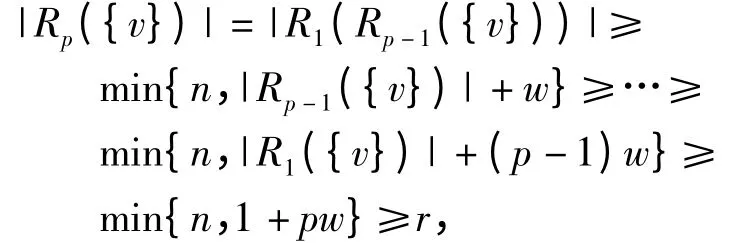
其中p=「(r-1)/w⏋. 结合k 点r-指数的定义即得结论.

若D NDn，w，注意到:NDn，w⊆Bn，w，故类似可得结论. □

对于完全不可分、几乎可分方阵(有向图)，可进一步求得其k 点r-指数的上确界.

设D1是顶点集为V={i|1≤i≤n}、弧集为E={(i，i+1)，(i +1，i)|1≤i≤n -1}∪{(1，1)，(n，n)}的有向图(图1).显然，D1NDn⊆Fn⊆Pn.

图1 有向图D1Figure 1 Digraph D1

定理2 设D Fn(或D NDn)，则pr(D，k)≤r-1，此上界可达且D1是极图之一.

证明 若D Fn=Bn，1，由定理1 可得pr(D，k)≤r-1. 下面仅需证明pr(D1，k)=r -1 即得结论.一方面，由于D1Fn=Bn，1，根据定理1，pr(D1，k)≤r-1.另一方面，可直接验证:对于任意顶点v V(D1)，以及满足t ≤r - 2 的任意非负整数t，|Rt({v})| =t+1≤r -1，故pr(D1，k)≥r -1. 综上可得:pr(D1，k)=r-1.

类似地，若D NDn= NDn，1，不难发现D1NDn，结合定理1 即得:pr(D，k)≤r -1，此上界可达且D1是极图之一. □

注意到:当r =n 时，k 点n-指数即是广为研究的k 点指数［3］.由定理2 立可推出完全不可分方阵和几乎可分方阵其k 点指数的上确界.

推论1 设D Fn(或D NDn)，则其k 点指数p(D，k)=pn(D，k)≤n-1，此上界可达且D1是极图之一.

1.2 第k 重上r-指数

引理1［4］设n，k，r 是满足1≤k，r≤n 的正整数，D 是一个n 阶本原有向图，则Fr(D，k)=0 当且仅当k≥r.

根据引理1，本节默认假设k ＜r.

定理3 设D Bn，w(或D NDn，w)，其中1≤w＜n，则Fr(D，k)≤「(r-k)/w⏋.

证明 若D Bn，w(1≤w ＜n)，由其图论意义可知:任一k (1 ≤k ≤n)点子集X ⊆V(D)都有|R1(X)|≥min{n，k +w}，从而对于∀X⊆V(D)且|X| =k，有其中p =「(r -k)/w⏋.根据第k 重上r-指数的定义可得:Fr(D，k)≤p=「(r-k)/w⏋.

若D NDn，w，由于NDn，w⊆Bn，w，同理可证得结论. □

下面给出完全不可分方阵(有向图)和几乎可分方阵(有向图)其第k 重上r-指数的上确界.

设Dk(1≤k≤n)表示顶点集为V ={i|1≤i≤n}、弧集为E ={(i，k +1)，(k +1，i)|1≤i≤k}∪{(i，i+1)，(i+1，i)|k+1≤i≤n-1}∪{(i，i)|1≤i≤k，或i=n}的有向图(图2).易见，DkNDn⊆Fn⊆Pn(1≤k≤n).

图2 有向图Dk(1≤k≤n)Figure 2 Digraph Dk(1≤k≤n)

关于本原有向图Dk的第k 重上r-指数有如下的结论:

引理2 Fr(Dk，k)=r-k.

证明 一方面，由于DkNDn=NDn，1⊆Fn=Bn，1，由定理3 可得:Fr(Dk，k)≤r -k. 另一方面，取k 点子集X={1，…，k}，易见:对于满足t≤r -k -1的任意非负整数t，均有|Rt(X)| =k +t≤r -1，故Fr(Dk，k)≥r-k.综上可得结论成立. □

定理4 设D Fn(或D NDn)，则Fr(D，k)≤r-k，此上界可达且Dk是极图之一.

证明 对于D Fn=Bn，1(或D NDn=NDn，1)，由定理3 可得:Fr(D，k)≤r -k. 又因DkNDn⊆Fn，结合引理2 即得结论. □

当r =n 时，第k 重上n-指数正是第k 重上指数［3］.根据定理4 可得完全不可分方阵和几乎可分方阵其第k 重上指数的上确界.

推论2 设D Fn(或D NDn)，则其第k 重上指数F(D，k)=Fn(D，k)≤n -k，此上界可达且Dk是极图之一.

2 含特殊圈结构的本原有向图的广义本原r-指数

首先介绍下文需要用到的若干重要引理.

引理3［1］D Pn当且仅当D 是一个n 阶的强连通有向图，且D 中所有不同圈长的最大公因数等于1.

设D Pn.以R=R(D)表示D 中所含的若干不同圈长之集，又记从点u 到点v 且与R 中每种长度的圈均相交的最短途径之长为dR(u，v).设R={c1，…，cs}(s≥2)表示一个互质的正整数集，以φ(R)=φ(c1，…，cs)表示互质正整数c1，…，cs的Frobenius数.关于Frobenius 数的定义及有关结论可参见文献［1］，其中一个重要的结论如下:

引理4［1］设c1、c2是互质的正整数，则φ(c1，c2)=(c1-1)(c2-1).

引理5［1］设D Pn，且c1，c2，…，cs(s≥2)是D 中若干不同的圈长，其中ci≠cj(1≤i ＜j≤s)，g.c.d.(c1，c2，…，cs)=1 (g. c. d. 表示最大公因数).令R={c1，c2，…，cs}.那么，对于满足t≥dR(i，j)+φ(R)的非负整数t，必然存在一条从点i 到点j的长为t 的途径.

引理6［10］设D Pn，且X 是一个非空点子集，即∅≠X⊆V(D).则对于任意非负整数t，都有

接下来给出几类含特殊圈结构的本原有向图的定义.

定义1［11］设D Pn，且C ={C1，C2，…，Cs}(s≥2)是其若干不同长度的有向圈构成的一个子集，并记有向圈Cq的长度为cq(q =1，2，…，s). 若c1＞c2＞… ＞cs≥1，g. c. d. (c1，c2，…，cs)=1，且所有有向圈Cq(q=1，…，s)有m (≥1)个公共点，即V(Cq)| =m，则称D 为含交圈结构的本原有向图.记含交圈结构的n 阶本原有向图之集为CIPn.

定义2［10，12］设A=(aij) Bn.若∀1≤i ＜j≤n都有aij=aji=1，则称A 为对称矩阵，D(A)为对称有向图;若存在1≤i ＜j≤n 满足aij=aji=1，则称A为微对称矩阵，D(A)为微对称有向图.记n 阶对称本原矩阵(有向图)之集为SPn，n 阶微对称本原矩阵(有向图)之集为MSPn.

下面将从含多圈结构的本原有向图出发展开研究，逐步探讨若干含特殊圈结构的本原有向图其4类广义本原r-指数的上界问题.为方便叙述，采用图论的语言来刻画主要结论.如无特别说明，默认假设n，k，r 是满足1≤k，r≤n 的正整数.

2.1 第k 重上r-指数

根据引理1，此节均默认假设k ＜r.

定理5 设D Pn，且C1，…，Cs(s≥2)是D 中若干不同长度的有向圈，又记有向圈Cq的长度为cq(q=1，…，s)，且R={c1，…，cs}，其中c1＞…＞cs≥1，g.c.d.(c1，…，cs)=1.则

证明 对于任意的非空k 点子集X，构建从X出发且与R 中每种长度的有向圈均相交的最短途径:记从X 出发到有向圈C1的最短途径为W1，易见W1的长度l1≤max{0，(n-c1)+(1-k)};又记从X 出发经有向圈C1再到有向圈C2的最短途径为W1+W2，则W1+W2的长度(1－k)};以此类推，可找到一条从X 出发依次经过有向圈C1，…，Cs-1最终到达有向圈Cs的最短途径W1+W2+… +Ws，其总长度为

必然存在从点x 到点ys的长为p - i 的途径，则Rp({x})⊇Ri({ys}).因此，结合引理6 可得:

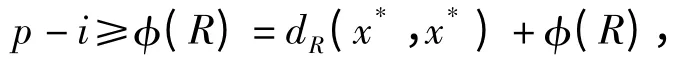
所以存在从点x*到其自身长为p -i 的途径. 结合引理6 可得:

综上，结合第k 重上r-指数的定义可得结论. □

定理5 刻画了含多圈结构的本原有向图其第k重上r-指数的上界.采用类似的方法，接下来考虑含交圈结构的本原有向图.

定理6 设D CIPn，且D 中含有若干不同长度的有向圈C1，…，Cs(s≥2)，记其长度分别为c1，…，cs，令R={c1，…，cs}，其中c1＞…＞cs≥1，g.c.d.(c1，…，cs)=1，且|V(Cq)| =m(≥1).则

情形1:n-m-k ＜0.易见，|X∩Z|≥m +k -n≥1，即X∩Z≠∅.注意到:从X∩Z 中的任一点x 出发到其自身与R 中每种长度的有向圈均相交的最短途径之长为0，即dR(x，x)=0. 又由引理5，对于非负整数i=0，…，(n -m)+(r -k)，因为p -i≥φ(R)=dR(x，x)+φ(R)，所以存在从点x 到其自身长为p-i 的途径.结合引理6 可得:

情形2:n -m -k≥0.记从X(不妨设为点x X)出发到Z(不妨设为点z Z)的最短途径为W，则W 的长度d≤n+1 -k-m(＞0).由于W 是从点x X 到点z Z 且与R 中每种长度的有向圈均相交的最短途径，故dR(x，z)≤(n -m)+(1 -k). 根据引理5，对于非负整数i=0，…，r-1，由于

必然存在从点x 到点z 的长为p - i 的途径，从而Rp({x})⊇Ri({z}).再结合引理6 可得:

根据第k 重上r-指数的定义，综上可得结论. □

作为定理5 及定理6 的特殊情况，令s=2(即所考虑的圈结构由2 种不同长度的有向圈构成)，结合引理4 有以下的推论.

推论3 设D Pn，且C1，C2是D 中长度分别为c1，c2的有向圈，其中c1＞c2≥1，g.c.d.(c1，c2)=1.则

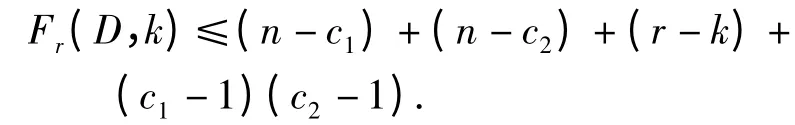
推论4 设D CIPn，且C1，C2是D 中长度分别为c1，c2的有向圈，其中c1＞c2≥1，g.c.d.(c1，c2)=1，且|V(C1)∩V(C2)| =m(≥1).则

注1 对上述几个定理和推论中的圈长等变量赋值，可导出更多有趣的结论. 例如:令推论4 中的c1=3，c2=m =2，有Fr(D，k)≤n +r -k，这正是文献［4］的定理5.6.

下面进一步特殊化本原有向图的圈结构，分别研究n 阶微对称有向图集MSPn和n 阶对称本原有向图集SPn的第k 重上r-指数.

定理7 设D MSPn，则

证明 由于D MSPn，结合引理3 可知:D 中含有长度分别为2 和c 的有向圈，其中c 是奇数，即g.c.d.(2，c)=1.则利用推论3 即得结论. □

定理8 设D SPn，则

证明 因为D SPn，所以D 中每一个点均落于一个长为2 的有向圈上，又结合引理3 可知:D 中必含一个长为奇数c 的有向圈C.

令p=(n -1)+(r -k)，R ={2，c}. 由引理4知:φ(R)=φ(2，c)=c -1.对于任意的非空k 点子集X，分2 种情形讨论从X 出发到C 的最短途径:

情形1:n-c -k ＜0.显然，|X∩V(C)|≥c +k-n≥1，即X∩V(C)≠∅.注意到:从X∩V(C)中的任一点x 出发到其自身与R 中每种长度的有向圈均相交的最短途径之长为0，即dR(x，x)=0.根据引理5，对于非负整数i =0，…，(n - c)+ (r - k)，由于p-i≥c-1 =dR(x，x)+φ(R)，故有从点x 到其自身长为p-i 的途径.从而结合引理6 可得:|Rp(X)|≥|Rp(X∩V(C))|≥|Ri(X∩V(C))|≥(c+k-n)+［(n-c)+(r-k)］=r.

情形2:n -c -k≥0. 记从X(不妨设为点x X)出发到C(不妨设为点y C)的最短途径为W，则W 的长度d≤n+1 -k-c(＞0).由于W 是从点x X 到点y C 且与R 中每种长度的有向圈均相交的最短途径，故dR(x，y)≤(n -c)+(1 -k). 根据引理5，对于非负整数i=0，…，r-1，由于

必存在从点x 到点y 的长为p - i 的途径，从而Rp({x})⊇Ri({y}).故由引理6 可得:

根据第k 重上r-指数的定义可得结论. □

对比分析定理6 和定理8 的证明过程，我们发现，定理6 还可作下列形式的推广(证明类似于定理6，此处略).

定理9 设D Pn，且D 中含有长度为cq的若干个有向圈Cq，1，…，Cq，tq，其中cq，tq是正整数，q =1，…，s(s≥2).又设ci≠cj(1≤i ＜j≤s)，R={c1，…，cs}，g.c.d.(c1，…，cs)=1，且=m(≥1).则

注2 易见，由定理9 可直接导出定理8.另外，定理9 还可推出带环的本原有向图其第k 重上r-指数的上界(见文献［4］的定理5.2).

2.2 第k 重下r-指数

引理7［4］设n，k，r 是满足1≤k，r≤n 的正整数，D 是一个n 阶本原有向图，则fr(D，k)=0 当且仅当k≥r.

由引理7，本节默认假设k ＜r.

定理10 设D Pn，且D 中含有长度为cq的若干个有向圈Cq，1，…，Cq，tq，记Vq=V(Cq，j)，其中cq，tq均是正整数，q =1，…，s(s≥2). 又设ci≠cj(1≤i ＜j≤s)，R={c1，…，cs}，g.c.d.(c1，…，cs)=1，Z，且|Z| =m(≥1)，其中l {1，…，s}.则

证明 若k≤m，取非空k 点子集X⊆Z;若k ＞m，取非空k 点子集X⊇Z.构建从X∩Z 出发且与R中每种长度的有向圈均相交的最短途径:显然，X∩Z中的任一点均与长度为c1，…，cl的有向圈相交;记从X∩Z 出发到Vl+1的最短途径为Wl+1，易见Wl+1的长度rl+1≤max{0，(n - |Vl+1|)+(1 -min{k，m})};又记从X∩Z 出发经长度分别为c1，…，cl，cl+1的有向圈再到Vl+2的最短途径为Wl+1+Wl+2，则Wl+1+Wl+2的长度rl+1+rl+2≤max{0，Σq=l+1，l+2(n- |Vq|)+(1-min{k，m})};以此类推，可找到一条从X∩Z 出发依次经过长度分别为c1，…，cl，cl+1，…，cs-1的有向圈最终与长度为cs的有向圈相交(即到达点集Vs)的最短途径Wl+1+…+Ws，其总长度为

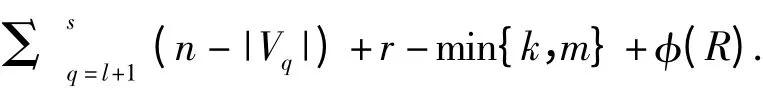
根据引理5，对于非负整数i=0，…，r-1，由于

必然存在从点x 到点ys的长为p - i 的途径，则Rp({x})⊇Ri({ys}).结合引理6 可得:|Rp(X)|≥

即X∩Z ∩Vl+1∩…∩Vs≠∅.此时X∩Z∩Vl+1∩…∩Vs中的任一点x*到其自身且与R 中每种长度的有向圈均相交的最短途径之长为0，即dR(x*，x*)=0.根据引理5，对于非负整数i=0，…(n-|Vq|)+r-min{k，m}，因为

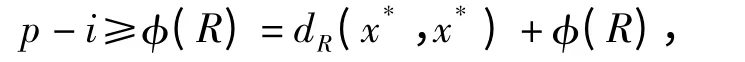
所以存在从点x*到其自身长为p -i 的途径. 则由引理6 可得:

根据第k 重下r-指数的定义，综上可得结论. □

在定理10 中令l=s，且tq=1 (q =1，…，s)，易得关于D CIPn其第k 重下r-指数的上界:

推论5 设D CIPn，且D 中含有若干不同长度的有向圈C1，…，Cs(s≥2)，记其长度分别为c1，…，cs，令R ={c1，…，cs}(c1＞… ＞cs≥1)，g. c. d.(c1，…，cs)=1，且|V(Cq)| =m(≥1).则

进一步地，若D CIPn中的圈结构是由2个不同长度的有向圈所构成的，即在推论5 中令s=2，结合引理4 即得以下结论:

推论6 设D CIPn，且C1，C2是D 中长度分别为c1，c2的有向圈，其中c1＞c2≥1，g.c.d.(c1，c2)=1，且|V(C1)∩V(C2)| =m(≥1).则

下面分别研究n 阶微对称有向图集MSPn和n阶对称本原有向图集SPn的第k 重下r-指数的上界.

引理8［4］设D 是一个n 阶的本原有向图且其最短圈长为g，其中n，k，r，g 是满足1≤g≤k ＜r≤n的正整数.则fr(D，k)≤r-k 且该上界可达.

对应于推论6，若考虑D Pn中的圈结构是由2个不同长度的有向圈所构成，但这2个有向圈无公共部分，即在定理10 中令s =2，t1=t2=1，l =1，结合引理4 可得下述推论:

推论7 设D Pn，且C1，C2是D 中长度分别为c1，c2的有向圈，其中V(C1)∩V(C2)=∅，c1≠c2，g.c.d.(c1，c2)=1.则

定理11 设D MSPn.则

证明 因为D MSPn，所以由引理3 可知:D中含有长度分别为2 和c 的有向圈，其中c 是奇数，即g.c.d.(2，c)=1，且D 的最短圈长g≤2.

若k≥2，则k≥2≥g，由引理8 可得:fr(D，k)≤r-k.

若k=1，且D 中长度分别为2 和c 的有向圈有公共点(即m≥1)，则由推论6 可得:fr(D，1)≤r -min{1，m}+(2 -1)(c-1)=r+c-2≤r+n-2.

若k=1，且D 中长度分别为2 和c 的有向圈无公共点，则根据推论7，有fr(D，1)≤(n -c)+(r -min{1，2})+(2 -1)(c-1)≤r+n-2. □

定理12 设D SPn且最短奇圈长为c.则

证明 若k≥2，又因D SPn的最短圈长g≤2，所以k≥2≥g，则根据引理8 可得:fr(D，k)≤r-k.

若k=1，由于D SPn，故D 中每一个点均落于一个长为2 的有向圈上，即D 中长度分别为2 和c的有向圈必有公共点(即m≥1)，则由推论6 可得:

2.3 k 点r-指数

引理9［4］设n，k，r 是满足1≤k，r≤n 的正整数，D 是一个n 阶本原有向图.则pr(D，k)=0 当且仅当r=1.

根据引理9，本节均默认假设r ＞1.

定理13［4］设D Pn，且D 中含有长度为cq的若干个有向圈Cq，1，…，Cq，tq，其中tq是正整数，q=1，…，s(s≥2).又设R={c1，…，cs}，c1＞…＞cs≥1，g.c.d.(c1，…，cs)=1，且|V(Cq，j))|=m(≥1).那么，

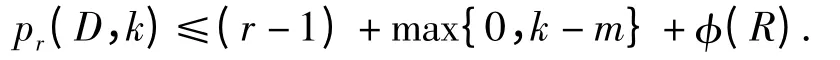
必然存在从点x 到点z 的长为p - i 的途径，从而Rp({x})⊇Ri({z}). 故结合引理6，对于每一个顶点从而根据k 点r-指数的定义可得结论. □

推论8 设D CIPn，且D 中含有若干不同长度的有向圈C1，…，Cs(s≥2)，记其长度分别为c1，…，cs，令R={c1，…，cs}，其中c1＞… ＞cs≥1，g. c. d.(c1，…，cs)=1，且|则

证明 在定理13 中令tq=1 (q =1，…，s)，即得结论. □

上述结论主要刻画了含交圈结构的本原有向图其k 点r-指数的上界.接下来将分别探讨D MSPn和D SPn的k 点r-指数.

引理10 设D Pn，且C1，C2是D 中长度分别为c1，c2的有向圈，其中V(C1)∩V(C2)=∅，c1＞c2≥1，g.c.d.(c1，c2)=1.则

证明 由于D Pn且V(C1)∩V(C2)=∅，考虑从C1(不妨设为点y1)到C2(不妨设为点y2)的最短途径W，易见其长度d≤n+1 -c1-c2(＞0).又因为D 是强连通的(见引理3)，故可取非空k 点子集X⊇{y1}，且对于点x X 均有长度为dx≤k -1 的途径可达点y1.故∀x X，存在从点x 出发经点y1最终到达点y2的途径，其长度为dx+d，即dR(x，y2)≤dx+d≤n +k -c1-c2，其中R ={c1，c2}. 令p=n+r +k +c1c2-2c1-2c2. 由引理4 和引理5，对于非负整数i=0，…，r-1，因为

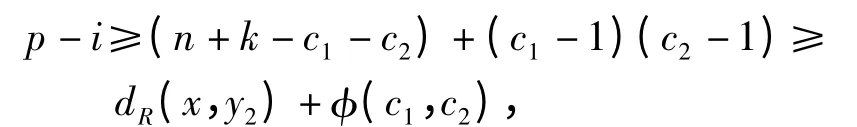
所以必存在从点x 到点y2的长为p-i 的途径，从而Rp({x})⊇Ri({y2}).故对于每一个顶点x X，结合引理6，根据k点r-指数的定义可得结论. □

定理14 设D MSPn，则

证明 由于D MSPn，根据引理3 可知:D 中含有长度分别为2 和c 的有向圈，其中c 是奇数，即g.c.d.(2，c)=1.

若D 中长度分别为2 和c 的有向圈有公共点(即m≥1)，当m=1 时，c≤n-1;当m=2 时，c≤n.根据推论8 和引理4，令s=2，有:pr(D，k)≤(r-1)+max{0，k-m}+(c-1)≤n+r+k-4.

若D 中长度分别为2 和c 的有向圈无公共点，则由引理10 可得:pr(D，k)≤n +r +k +2c -4 -2c=n+r+k-4. □

定理15 设D SPn且最短奇圈长为c. 则pr(D，k)≤r-2 +max{c，k}.

证明 因为D SPn，所以D 中每一个点均落于一个长为2 的有向圈上.根据定理13，令s =2，c1=2，c2=c，则m=c，再结合引理4，有:

2.4 k 点r-同位指数

引理11［4］设n，k，r 是满足1≤k，r≤n 的正整数，D 是一个n 阶本原有向图，则sr(D，k)=0 当且仅当k=r=1.

根据引理11，本节均默认假设k+r ＞2.

定理16 设D CIPn，且D 中含有若干不同长度的有向圈C1，…，Cs(s≥2)，记其长度分别为c1，…，cs，令R ={c1，…，cs}，其中c1＞… ＞cs≥1，g. c. d.(c1，…，cs)=1，且则

必然存在从点x 到点z 的长为p - i 的途径，则Rp({x})⊇Ri({z}).由引理6 可知:|({z})|≥r，不妨设({z})⊇{v1，…，vr}.故∀x X，均有Rp({x})⊇({z})⊇{v1，…，vr}，从而由k 点r-同位指数的定义即得结论. □

定理17 设D SPn且最短奇圈长为c. 则sr(D，k)≤k+r+c-3.

证明 因为D SPn，所以D 中长度分别为2和c 的有向圈必有公共点.结合定理16 和引理4 可得结论. □

［1］柳柏濂. 组合矩阵论［M］. 北京:科学出版社，2005.

［2］柳柏濂，黄宇飞. 组合矩阵的结构指数［M］. 北京:科学出版社，2015.

［3］Brualdi R A，Liu B L. Generalized exponents of primitive directed graphs ［J］. Journal of Graph Theory，1990，14:483 -499.

［4］Huang Y F，Liu B L. Generalized r-exponents of primitive digraphs［J］. Taiwanese Journal of Mathematics，2011，15:1999 -2012.

［5］Liu B L. Generalized exponents of Boolean matrices［J］.Linear Algebra and Its Application，2003，373:169 -182.

［6］Brualdi R A，Shao J Y. Generalized exponents of primitive symmetric digraphs［J］. Discrete Applied Mathematics，1997，74:275 -293.

［7］You L H，Liu B L，Shen J. r-Indecomposable and rnearly decomposable matrices［J］. Linear Algebra and Its Application，2005，407:105 -116.

［8］周积团. r-不可分矩阵的本原指数［J］. 数学的实践与认识，2003，33(5):96 -98.Zhou J T. Primitive expotents of r-indecomposable matrices［J］. Mathematics in Practice and Theory，2003，33(5):96 -98.

［9］周积团. r-不可分矩阵的本原指数(Ⅱ)［J］. 数学理论与应用，2003，23(2):124 -128.Zhou J T. Primitive expotents of r-indecomposable matrices:Ⅱ［J］. Mathematical Theory and Application，2003，23(2):124 -128.

［10］Liu B L. On fully indecomposable exponent for primitive Boolean matrices with symmetric ones［J］. Linear and Multilinear Algebra，1992，31:131 -138.

［11］Huang Y F，Liu B L. On a conjecture for fully indecomposable exponent and Hall exponent［J］. Linear and Multilinear Algebra，2010，58:699 -710.

［12］陈佘喜. 对称本原图的集指数与本原简单图的广义上指数的极图［J］. 应用数学学报，2005，28(2):243 -252.Chen S X. The set exponent of symmetric primitive digraphs and the extremal graphs of the kth upper generalized exponent for primitive simple graphs［J］. Acta Mathematicae Applicatae Sinica，2005，28(2):243 -252.