Gorenstein n-余挠模及Gorenstein n-余挠维数
2015-12-14黄俊红张翠萍
黄俊红,张翠萍
(西北师范大学数学与统计学院,兰州730070)
2002年,Lee[1]给出了n-凝聚环的定义.2009年,Bennis[2]给出了左GF- 闭环的概念. 2014年,Gao[3]在左GF-闭环上研究了模和环的Gorenstein余挠维数的相关性质;Selvaraj 等[4]给出了n-绝对纯模、Gorenstein n-平坦模及Gorenstein n-余挠模的定义,在右n-凝聚环上讨论了Gorenstein n-平坦模的相关性质.
本文在右n-凝聚环上研究了Gorenstein n-余挠模及模和环的Gorenstein n-余挠维数的相关性质,得到Gorenstein n-余挠模的Gorenstein n-平坦覆盖是Gorenstein n-余挠模,证明了在右n-凝聚环上,所有Gorenstein n-平坦左R-模的投射维数不超过1 等价于任意内射左R-模的商模是Gorenstein n-余挠的.
1 基本概念
设C是左R-模所构成的类.由文献[5],称φ:M→C 是M 的C-包络,如果满足以下2 条:
(1)对任意左R-同态f:M→C',存在左R-同态g:C→C',使得gφ =f,或者说序列HomR(C,C')→HomR(M,C')→0 是正合的,其中C,C' C;
(2)当C' =C,f =φ 时,满足gφ =f 的左R-同态g 必是C 上的自同构.
若只有(1)成立,则称φ:M →C 是M 的C-预包络.
C-预覆盖和C-覆盖也可对偶地定义.
设L,C分别是左R 模的类.我们将L的左、右正交类分别记作:
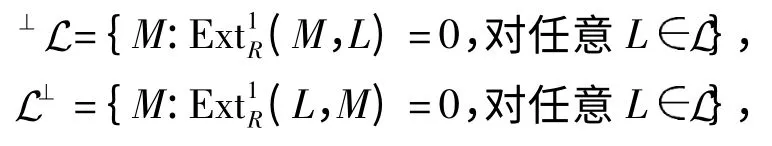
其中M 是任意左R-模.
由文献[5],称(L,C)是余挠理论,如果L⊥=C,⊥C=L.由文献[6],称余挠理论(L,C)是完备的,如果每一个左R-模都有一个L-覆盖和C-包络. 称余挠理论(L,C)是遗传的,如果对任意左R-模的短正合列0→C'→C→C″→0,若C,C' C,则C″ C.
设F是左R 模所构成的类,Proj(R),Inj(R)分别表示投射模类和内射模类.由文献[7],有
(1)称F是投射可解类,如果满足:
(a)Proj(R)⊆F;
(b)在任意R-模的短正合列0→F'→F→F″→0 中,若F″ F,则F F当且仅当F' F.
(2)称F是内射可解类,如果满足:
(a)Inj(R)⊆F;
(b)在任意R-模的短正合列0→F'→F→F″→0 中,若F' F,则F F当且仅当F″ F.
为了方便,本文中的环均指有单位元的结合环,模均指酉模. 对任意R-模M,pdR(M)、fdR(M)和idR(M)分别表示M 的投射维数、平坦维数和内射维数.同时,在不指明左模或右模时都指左模.
2 n-余挠模及n-平坦模
定义1[4]称左R-模M 是n-平坦的,如果对任意投射维数不超过n 的有限表示右R-模N,有一般将n-平坦模所做成的模类记作Fn.
定义2[4]称左R-模M 是n-余挠模,如果对任意N Fn,有将n-余挠模所做成的模类记作Cn.
注记1 (1)设n、m 是任意非负整数,并且若n≥m,则Fm⊆Fn.因此n-余挠模是m-余挠模.
(2)内射模一定是n-余挠模,并且有包含关系:内射模类⊆n-余挠模类⊆余挠模类.
引理1 对任意交换环R,设N 是n-平坦R-模,且F 是平坦模.则N⊗RF 是n-平坦R-模.
证明 任取投射维数有限的有限表示R- 模C.则存在正合列0→K→P→C→0,其中P 是有限生成投射R-模.下证(C,N⊗F)=0.
用-⊗R(N⊗F)作用以上正合列,可得如下交换:
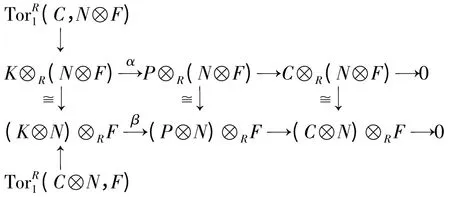
命题1 设R 是交换环,则以下条件等价:
(1)M 是n-余挠模;
(2)对任意平坦R-模F,HomR(F,M)是n-余挠模;
(3)对任意投射R-模P,HomR(P,M)是n-余挠模.
证明 (1)⇒(2).设N 是任意n-平坦R-模,则有正合列0→K→P→N→0,其中P 是投射R-模.对任意平坦R-模F,用-⊗RF 作用到上述正合列上,可得正合列
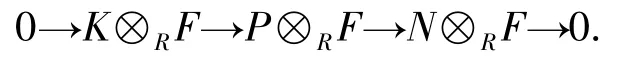
由引理1 可知N⊗RF 是n-平坦R-模. 用HomR(-,M)作用到上述正合列上,可得:

由文献[8]的定理5 可得:HomR(P,HomR(F,M))→HomR(K,HomR(F,M))→0,从而有正合列HomR(P,HomR(F,M))→HomR(K,HomR(F,M))(N,HomR(F,M))→(P,HomR(F,M))=0.因此,(N,HomR(F,M))=0,故HomR(F,M)是n-余挠模.
(2)⇒(3).投射模是平坦模,结论显然成立.
(3)⇒(1).取P =R,由同构式HomR(R,M)≅M 可知结论成立.证毕.
3 Gorenstein n-余挠模
定义3[3]称环R 是右(左)n-凝聚的(n >0或n=∞),如果任意自由右(左)R-模的投射维数不超过n-1 的有限生成子模是有限表示的.称环R是n-凝聚环,如果环R 既是左n-凝聚的,又是右n-凝聚的.
定义4[4]称左R-模M 是n-绝对纯的,如果对任意投射维数不超过n 的有限表示左R 模N,有(N,M)=0.显然,内射模一定是n-绝对纯的.
定义5[4]称左R-模M 是Gorenstein n-平坦的,如果存在n-平坦左R-模的正合序列
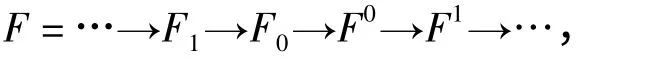
使得M≅Im(F0→F0),并且复形E⊗RF 是正合的,其中E 是任意n-绝对纯右R-模.将Gorenstein n-平坦模所做成的模类记作GFn.
定义6[4]称左R-模M 是Gorenstein n-余挠的,如果对任意Gorenstein n-平坦左R-模N,有(N,M)=0. 将Gorenstein n-余挠模所做成的模类记作GCn.
注记2 设R 是环,则有以下包含关系:
(1)平坦模类⊆n-平坦模类⊆Gorenstein n-平坦类;
(2)Gorenstein n-余挠模类⊆n-余挠模类⊆余挠模类.
引理2 设R 是右n-凝聚环. 如果M 是任意Gorenstein n-余挠模,那么对任意Gorenstein n-平坦模N,有(N,M)=0,i≥1.
因为任意模都有投射分解,所以取N 的投射分解:

因为R 是右n-凝聚环,所以由文献[4]的推论3.6 知Ker fi(i≥0)是Gorenstein n-平坦的.设Ki=Ker fi.则(N,M)≅(Ki-1,M)=0 (i≥1).故结论成立.证毕.
命题2 设R 是右n-凝聚环,则Gorenstein n-余挠模类是内射可解类.
证明 显然内射模类⊆Gorenstein n-余挠模类.
设0→M'→M→M″→0 是R-模的短正合列.下证:若M' GCn,则M″ GCn⇔M GCn.
设N 是任意Gorenstein n- 平坦R- 模,用HomR(N,-)作用到上述正合列上,可得:
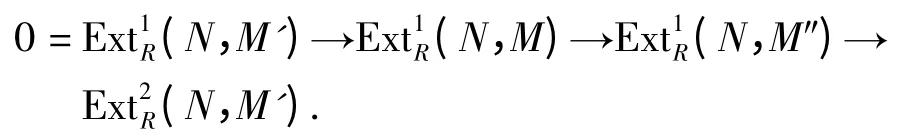
引理3[4]设R 是右n-凝聚环,则(GFn,GCn)是遗传的完备的余挠理论.
设M 是任意左R-模.由命题2 及引理3 可知,在右n-凝聚环上任意R-模都有满的Gorenstein n-平坦覆盖和单的Gorenstein n-余挠包络.以下将M 的Gorenstein n-平坦覆盖和Gorenstein n-余挠包络分别记作:GFn(M),GCn(M).
定理1 设R 是右n-凝聚环.则
(1)Gorenstein n-平坦模的Gorenstein n-余挠包络是Gorenstein n-平坦模;
(2)Gorenstein n-余挠模的Gorenstein n-平坦覆盖是Gorenstein n-余挠模.
证明 (1)设F 是任意Gorenstein n-平坦模.由引理3 可知F 有Gorenstein n-余挠包络φ:F →C,则有正合列0→F→C→L→0.根据Wakamutsu 引理有L GFn.由文献[4]的推论3.6 知,在右n-凝聚环R 上Gorenstein n-平坦R-模对扩张封闭,因此C GFn.
(2)设C 是Gorenstein n-余挠模. 由引理3 可知C 有Gorenstein n-平坦覆盖f:F →C,则有正合列0→K→F→C→0. 根据Wakamutsu 引理[5],K 是Gorenstein n- 余挠模. 因此由命题2 可知F 是Gorenstein n-余挠模.证毕.
定理2 设R 是右n-凝聚环.则下列条件等价:
(1)所有左R-模是Gorenstein n-余挠的;
(2)所有的Gorenstein n- 平坦左R- 模是Gorenstein n-余挠的;
(3)所有的Gorenstein n-平坦左R-模是投射的;
(4)对任意左R-同态f:M1→M2,若M1,M2是Gorenstein n- 余挠模,则Ker f 是Gorenstein n-余挠模.
证明 (1)⇒(2).结论显然成立.
(2)⇒(3). 设G 是任意Gorenstein n-平坦左R-模.则有正合列

其中P 是投射左R-模.因为R 是右n-凝聚环,所以K 是Gorenstein n-平坦的.因此(G,K)=0,即正合列可裂,故G 是投射左R-模.
(3)⇒(1).因为(Proj(R),RM)是余挠理论,所以结论显然成立.
(1)⇒(4).显然成立.
(4)⇒(2). 设M 是Gorenstein n-平坦左R-模,则有以下交换:

其中GCn(M)和GCn(L)分别表示M 和L 的Gorenstein n- 余挠包络. 由以上交换可知M = Ker ξ =Ker(δLξ),由条件(4)可知M 是Gorenstein n-余挠模,即条件(2)成立.证毕.
4 模和环的Gorenstein n-余挠维数
定义7 设R 是环,M 是左R- 模. 将M 的Gorenstein n-余挠维数记作Gn-cdR(M),定义为Gn-cdR(M)=inf{k|存在正合列0→M→C0→C1→…→Ck-1→Ck→0,其中CiGCn,0≤i≤k,k 为非负整数}.若这样的k 不存在,则记Gn-cdR(M)=∞.将环R 的左Gorenstein n-余挠整体维数记作l.Gn-cD(R)=sup{Gn-cdR(M)|M 是左R-模}.对偶地,将环R 的右Gorenstein n-余挠整体维数记作r.Gn-cD(R)=sup{Gn-cdR(M)|M 是右R-模}.特别地,若R 是交换环,则l.Gn-cD(R)=r.Gn-cD(R).
命题3 设R 是环,M 是左R-模,k 为非负整数,则下列条件等价:
(1)Gn-cdR(M)≤k;
(4)若序列0→M→C0→C1→…→Ck-1→Ck→0正合,并且若C0,C1,…,Ck-1是Gorenstein n-余挠左R-模,则Ck也是Gorenstein n-余挠左R-模;
(5)存在正合列0→M→C0→C1→…→Ck-1→Ck→0,其中C0,C1,…,Ck-1,Ck是Gorenstein n-余挠左R-模.
特别地,若R 是右n-凝聚环,则以上条件等价于:
(6)Gn-cdR(GFn(M))≤k.
证明 (1)⇔(2).由定义7 即可得证.
(2)⇒(3).由(2)可知,存在正合列

对任意Gorenstein n-平坦左R-模N,用HomR(N,-)作用以上正合列,由长序列引理[8]及维数转移公式[8]可得(N,Ck)≅(N,M). CkGCn,则由引理2 可得(N,Ck)=0. 因此(N,M)=0,i≥1.

(3)⇒(4).对任意Gorenstein n-平坦左R-模N,用HomR(N,-)作用到正合列上,由长序列引理及维数转移公式可得(N,Ck)≅(N,M)=0. 特别地,当i =1 时,(N,Ck)=0.故CkGCn.
(4)⇒(5). 因为任意R-模都有内射分解,所以结论显然成立.
(5)⇒(2).对任意Gorenstein n-平坦左R-模N,用HomR(N,-)作用到正合列

(1)⇔(6).若R 是右n-凝聚环,则由文献[4]的推论4. 8 可知M 有Gorenstein n- 平坦覆盖GFn(M),则有正合列

对任意Gorenstein n-平坦左R 模N,用HomR(N,-)作用到上述正合列上,由长序列引理可得:

在右n-凝聚环上Gorenstein n-平坦左R-模对扩张封闭,则由Wakamutsu 引理可知K 是Gorenstein n-余挠模.由引理2 可知(N,K)=0(N,K)=0.因此(N,GFn(M))≅(N,M).故条件(1)和条件(6)的等价性显然成立.证毕.
定理3 设R 是右n-凝聚环,k 为整数且k≥1,则以下条件等价:
(1)l.Gn-cD(R)≤k;
(2)所有Gorenstein n-平坦左R-模的投射维数不超过k;
(3)所有Gorenstein n-平坦左R-模的Gorenstein n-余挠维数不超过k;
(4)任意内射左R-模的商模的Gorenstein n-余挠维数不超过k-1;
(5)任意Gorenstein n-余挠左R-模的商模的Gorenstein n-余挠维数不超过k-1.
证明 (1)⇔(2)和(1)⇒(3)显然成立.
(3)⇒(2).设M 是任意左R-模.因为环R 是右n-凝聚环,所以M 有Gorenstein n- 平坦覆盖GFn(M).则有正合列0→K→GFn(M)→M→0.对任意Gorenstein n-平坦左R-模N,用HomR(N,-)作用以上正合列,可得:

因为环R 是右n-凝聚环,所以K 是Gorenstein n-余挠模.根据引理2(N,K)=0,由条件(3)可知(N,GFn(M))=0.因此(N,M)=0,故N 的投射维数不超过k.
(1)⇒(4). 设E 是任意内射左R-模,K 是E的子模.则有正合列
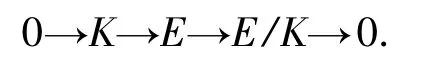
对任意Gorenstein n-平坦左R 模N,用HomR(N,-)作用以上正合列,可得:
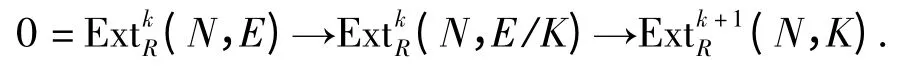
由条件(1)知Gn-cdR(K)≤k,因此(N,K)=0.因为(N,E)=0,所以(N,E/K)=0.故Gn-cdR(E/K)≤k-1.
(4)⇒(1).设M 是任意左R-模,则有正合列

其中E 是内射左R-模. 由条件(4)可知Gn- cdR(E/M)≤k-1,因为E GCn,所以Gn-cdR(M)≤k.故由M 的任意性可知条件(1)成立.
(4)⇒(5). 设M 是任意Gorenstein n-余挠左R-模,K 是M 的子模.则有正合列

和

其中E(K)是K 的内射包络.则有以下交换:
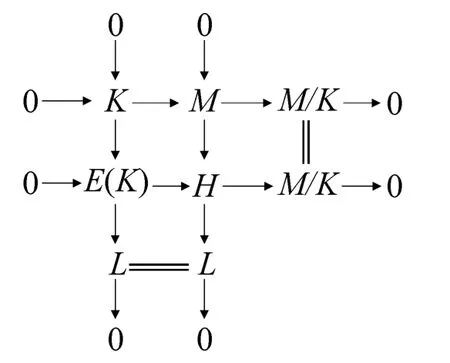
根据条件(4),Gn-cdR(L)≤k-1,则有正合列
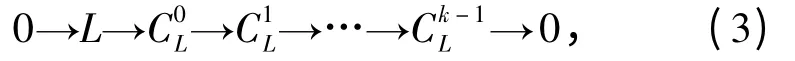
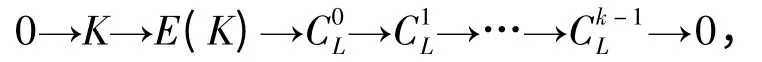
设左R-模M/K 的内射分解为0→M/K→E0→E1→…→Ek-2→Ek-1→….令C =Im(Ek-2→Ek-1),则有正合列

由正合列(1)、(4)可得正合列

因为Gn-cdR(K)≤k,所以C GCn. 因此Gn-cdR(M/K)≤k-1.证毕.
推论1 设R 是右n-凝聚环. 则以下条件等价:
(1)l.Gn-cD(R)≤1;
(2)所有Gorenstein n-平坦左R-模的投射维数不超过1;
(3)所有Gorenstein n-平坦左R-模的Gorenstein n-余挠维数不超过1;
(4)任意内射左R-模的商模是Gorenstein n-余挠的;
(5)任意Gorenstein n-余挠左R-模的商模是Gorenstein n-余挠的.
[1]Lee S B. n-coherent rings[J]. Communication in Algebra,2002,30(3):1119-1126.
[2]Bennis D. Rings over which the class of Gorenstein flat modules is closed under extensions[J]. Communication in Algebra,2009,37:855-868.
[3]Gao Z H. On Gorenstein cotorsion dimension over GF-closed rings[J]. Bulletin of the Korean Mathematical Society,2014,51(1):173-187.
[4]Selvaraj C,Udhayakumar R,Umamaheswaran A. Gorenstein n-flat modules and their covers[J]. Asia-European Journal of Mathematics,2014,7(3):1-13.
[5]Enochs E E,Jenda O M G. Relative homological algebra[M]. Belin:Walter de Gruyter,2000.
[6]Enochs E E,Jenda O M G,Lopez-Ramos J A. The existence of Gorenstein flat covers[J]. Mathematics Scand,2004,94(1):46-62.
[7]Holm H. Gorenstein homological dimensions[J]. Journal of Pure Application Algebra,2004,189:167-193.
[8]佟文廷. 同调代数引论[M].北京:高等教育出版社,1998.
