Effect of An Initial Stress on SH-Type Guided Waves Propagating in a Piezoelectric Layer Bonded on A Piezomagnetic Substrate

Guoquan Nie,2,Jinxi Liu,Ming Li

Effect of An Initial Stress on SH-Type Guided Waves Propagating in a Piezoelectric Layer Bonded on A Piezomagnetic Substrate

Guoquan Nie1,2,Jinxi Liu1,Ming Li1

Propagation of SH-type guided waves in a layered structure with an invariant initial stress is studied,where a piezoelectric thin layer is perfectly bonded on a piezomagnetic substrate.Both the layer and the substrate possess transversely isotropic property.The dispersion relations of SH waves are obtained for four kinds of different electro-magnetic boundary conditions.The effects of initial stress,thickness ratio and electro-magnetic boundary conditions on the propagation behaviors are analyzed in detail.The numerical results show that:1)The positive initial stresses make the phase velocity increasing,while the negative initial stresses decrease the phase velocity;2)The smaller the thickness ratio of a piezoelectric layer to a piezomagnetic substrate,the larger the phase velocity of SH-type guided wave propagating in the corresponding layered structure;3)The electrical boundary conditions play a dominant role in the propagating characteristics.Moreover the phase velocities for the electrically shorted surface are smaller than that for the open case.The obtained results are useful for understanding and design of the electromagnetic acoustic wave and microwave devices.

Piezoelectricmaterial;Piezomagneticmaterial;SHwave;Initialstress;Dispersion relation.

1 Introduction

Due to being able to facilitate the conversion between electrical energy and magnetic energy,piezoelectric/piezomagnetic composites or structures are potential candidates for magnetoelectric devices such as sensors,transducers, filters,delay lines,tunable phase shifters and resonators,etc.[Fiebig(2005);Nan,Bichurin,Dong,Viehland,and Srinivasan(2008)].These possible applications call for a bet-ter understanding of the static and dynamic behaviors of piezoelectric/piezomagnetic composite media,such as deformations,vibrations and wave propagation,etc.In recent years,the propagation behaviors of elastic waves in layered piezoelectric/piezomagnetic composites or structures have attracted increasing attention.Wang,Mai,and Niraula(2007)found that SH surface wave can exist in a transversely isotropic magneto-electro-elastic half-space open to the vacuum,and gave the explicit formulation of propagation velocity.Wei,Liu,and Fang(2009)demonstrated that three types of magneto-electric boundary conditions also support the propagation of SH surface waves.Liu,Fang,Wei,and Zhao(2008)studied Love waves in the structure of a piezoelectric layer bonded to a piezomagnetic halfspace or reverse con figuration.Based on the fully coupled constitutive relations,Calas,Otero,Rodríguez-Ramos,Monsivais,and Stern(2008)and Liu,Wei,and Fang(2010)investigated the dispersion relations of SH waves in a magnetoelectro-elastic layer between two different magneto-electro-elastic half-space and in piezoelectric-piezomagnetic periodically layered structure,respectively.Considering an imperfect interface between piezoelectric layer and piezomagnetic substrate,Nie,Liu,Fang,and An(2012)studied SH waves propagating in a bilayer coupled structure,and the effects of interfacial imperfection,electro-magnetic boundary conditions as well as the thickness ratio on the dispersion behaviors were discussed in detail.Duan,Zhang,Wang,and Yu(2014)studied wave propagating in a functionally graded piezoelectric-piezomagnetic rectangular ring.An analytical solution was derived by using double orthogonal polynomial series approach.Recently,Zakharenko(2013)reviewed the special topic of SH surface acoustic wave in piezoelectromagnetics or magneto-electro-elastic two-phase materials.

Because of the mismatch of material properties,the layered structures are most often subjected to internal residual stress.On the other hand,the layered piezoelectric system is usually prestressed during the manufacture process to avoid brittle fracture[Qian,Jin,Wang,and Kishimoto(2004)].As a result,research on the effect of the initial stress on the propagating behavior of elastic waves is very useful for the applications of piezoelectric-piezomagnetic composites.Du,Jin,and Wang(2007,2008)studied Love waves in a layered MEE half-space with or without initial stress,where the surface of the mechanically free layer is open to the vacuum or electrically short and magnetically open.As numerical examples,they illustrated the influences of initial stress,electromagnetic boundary conditions on the phase velocity,group velocity and magneto-electromechanical coupling factor of Love waves in the CoFe2O4/BaTiO3layered half-space.Zhang,Pang,and Feng(2014)explored the effect of initial stress on Rayleigh wave propagating in a magneto-electro-elastic half-space and the modes of mechanical displacement,electric potential,and magnetic potential are also discussed.They found that the initial stresses have important effect on the phase velocity and magneto-electromechanical coupling factor of Rayleigh wave.Zhang,Shen,and Du(2008)analyzed the effect of inhomogeneous initial stress on Love wave propagating in layered magneto-electro-elastic structures.The coupled magneto-electro-elastic field equations with variable coefficients are solved by adopting the Wentzel-Kramers-Brillouin approximate approach.And the influence of inhomogeneous initial stress on the phase velocity,corresponding coupled magneto-electric factor and stress fields are discussed numerically.Zhou,Lü,and Chen(2012)investigated the bulk wave propagation in laminated piezomagnetic/piezoelectric plates by using the state space approach,and the initial stresses as well as the interfacial imperfection were considered simultaneously.Mori,Narita,and Shindo(2011)investigated the response of clamped-free magnetostrictive/piezoelectric/magnetostrictive laminates under electric field.Based on the measured magnetostriction of the Terfenol-D/PZT/Terfenol-D laminate,the second-order magnetoelastic constants were evaluated by employing a nonlinear finite element analysis.The induced magnetic field and internal stresses for the laminates under electric field were also calculated.

In the present work,we investigate the SH-type guided waves propagating in a piezoelectric/piezomagnetic layered structure with an invariant initial stress.The dispersion equations of SH waves are obtained in closed form for four kinds of different electromagnetic boundary conditions at the surfaces of the layered system.The dispersion curves are plotted and discussed to reveal the influences of the electromagnetic boundary conditions,the initial stress and the thickness ratio on the propagation characteristics.

2 Problem formulations

For wave motion of small amplitude,the equilibrium equations for magneto-electroelastic materials with initial stress can be expressed in the following form[Du,Jin,and Wang(2007)]

where i,j,k=1,2,3.uiand σijare the components of displacement and stress,Diand Biare the electric displacement and magnetic induction,respectively.andare the initial stress,electric displacement and magnetic induction,respectively.ρ is the mass density.The subscript comma denotes a partial derivative with respect to the coordinates.

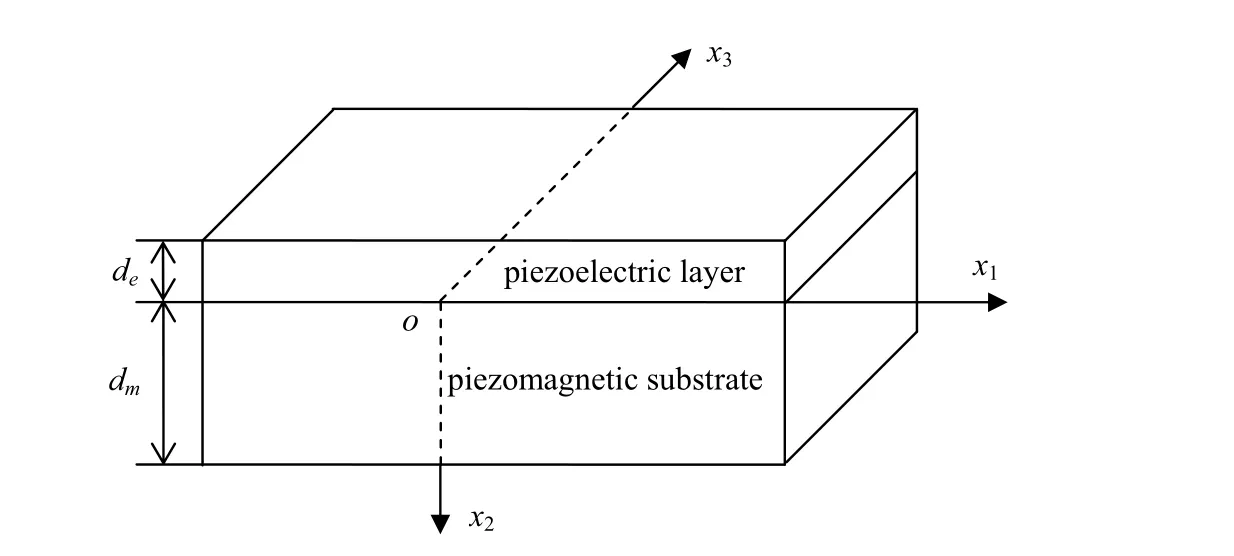
Figure 1:A piezoelectric layer/piezomagnetic substrate layered structure

Consider a layered structure consisting of a piezoelectric layer attached to a piezomagnetic substrate as shown in Fig.1.The piezoelectric and piezomagnetic materials are transversely isotropic,and their thicknesses are deand dm,respectively.For a SH wave propagating in x1direction,the components of displacement satisfy u1=u2=0,u3=u3(x1,x2,t),the electric potential is φ=φ(x1,x2,t),and magnetic potential ψ=ψ(x1,x2,t).In this case,the constitutive relation can be simplified into the following forms in terms of components[Soh and Liu(2006)]

for piezoelectric material and

for piezomagnetic material.In Eqs.(2)and(3),c44,e15,and h15are the elastic,piezoelectric and piezomagnetic constants,κ11and µ11are the dielectric permittivity and magnetic permeability,respectively.The superscripts“e”and “m”denote quantities corresponding to piezoelectric and piezomagnetic media,respectively.At the top(x2=-de)and bottom(x2=dm)surfaces of the layered structure,the traction free condition is given by

Different combinations of electric and magnetic conditions constitute four sets of electromagnetic boundary conditions at the two surfaces,that is

a)Electrically shorted and magnetically open case(denoted by “so”)

b)Electrically and magnetically shorted case(denoted by “ss”)

c)Electrically and magnetically open case(denoted by “oo”)

d)Electrically open and magnetically shorted case(denoted by “os”)

The continuous conditions at the interface(x2=0)are

3 SH wave solutions

In this study,only an invariant initial stressin the piezoelectric layer along x1-direction is considered.We also suppose that the external electric field and magnetic field are of absence.In this way,the initial electric displacement and initial magnetic induction in Eq.(1)can be omitted due to the higher order in finitesimal.By substituting Eqs.(2)and(3)into Eq.(1),the governing equations can be obtained as follows

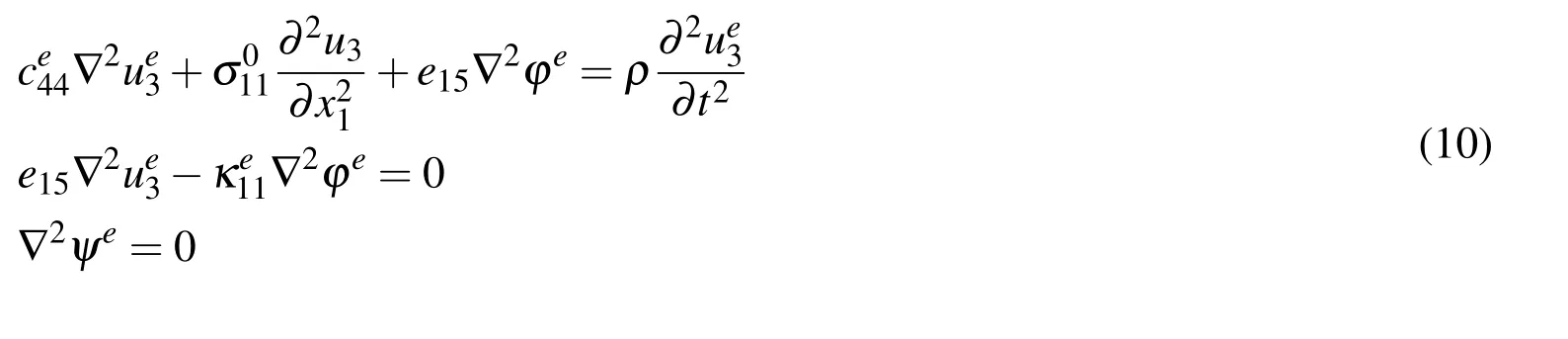
for piezoelectric material and

for piezomagnetic material,where

The solutions to Eqs.(10)and(11)can be written as

where k is the wave number.c is the phase velocity.andare functions to be determined.α=e,m.

By substituting Eq.(12)into Eqs.(10)and(11),we can obtain

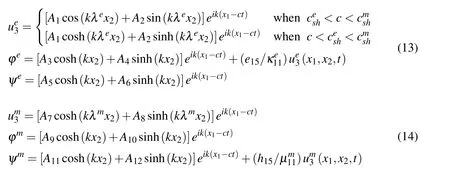
By using the constitutive relation(2)and(3),we can obtain the components of the stresses,electric displacements and magnetic inductions for piezoelectric material and piezomagnetic material as follows

4 Dispersion relations

By applying the boundary conditions(4)-(9)and the solutions drawn in previous section,we can obtain a set of equations for every kind of electro-magnetic boundary conditions.For the sake of brevity,we only derive the dispersion relation for electrically shorted and magnetically open boundary condition in Eq.(5).Substituting Eqs.(13)-(16)into Eqs.(4),(5)and(9),we have

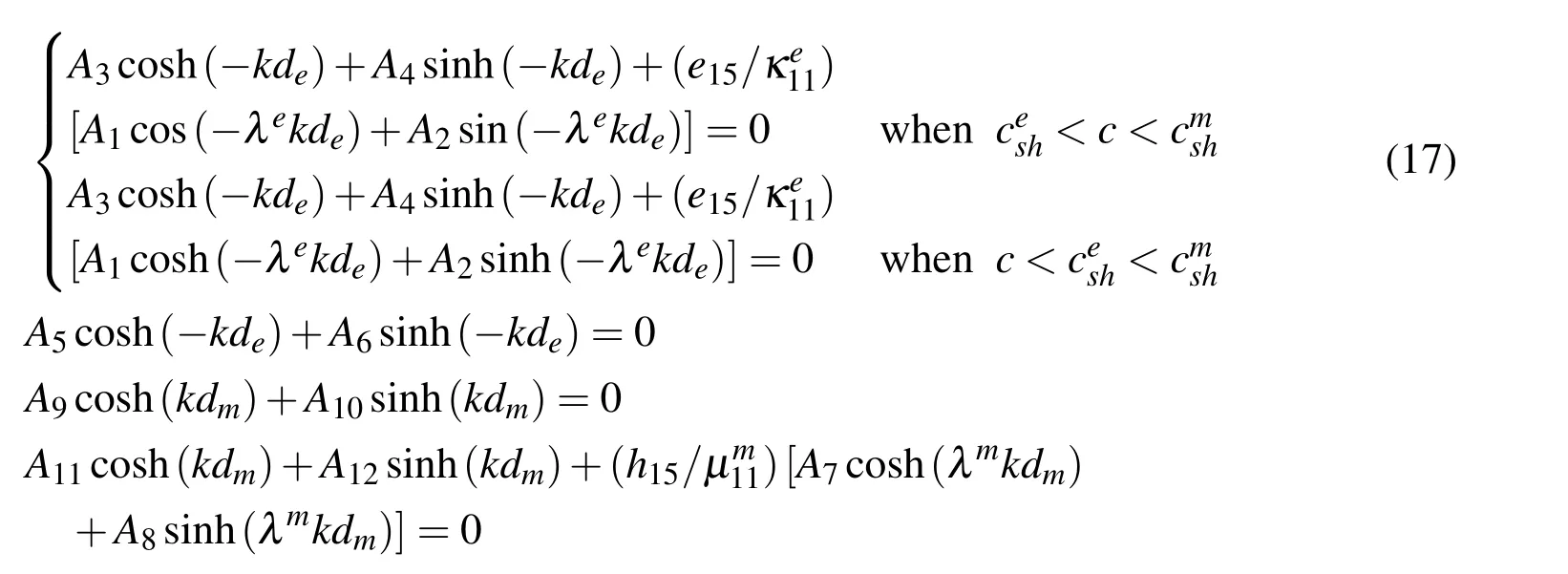
To obtain a nontrivial solution for Eq.(17),the determinant of the coefficients matrix must be zero.In this way,the dispersion equation for“so”boundary condition can be obtained.

Table 1:Material properties used in numerical examples

5 Numerical results

The materials used in numerical calculation are piezomagnetic CoFe2O4and piezoelectric PZT-5A.Their properties are listed in Table 1[Liu,Fang,Wei,and Zhao(2008);Luan,Zhang,and Wang(2005)].In the following figures,the horizontal axis is the non-dimensional wave number kde,and the vertical axis is the phase velocity of SH wave.f is the ratio of thickness of piezoelectric layer to piezomagnetic substrate.

5.1 Effect of the electro-magnetic boundary conditions

The dispersion curves of the first mode for four kinds of different boundary conditions are plotted in Fig.2,where the thickness ration f is taken as 0.1.Here,we assume that a compressive stress of 1GP is preloaded in the piezoelectric layer along x1-direction.From Fig.2,it can be observed that the phase velocities of the first mode for the “so”and “ss”cases are equal except when the non-dimensional wave number is very small.Similar feature can also be seen in the cases of“oo”and “os”.In addition,the wave velocities for the electrically shorted cases are smaller than electrically open cases.These results show that the electric boundary conditions dominate the dispersion characteristics of SH waves and the effects of the magnetic boundary conditions can not be considered.

Figure 2:Dispersion curves of the first mode for four kinds of electro-magnetic boundary conditions

5.2 Effect of the initial stresses

In order to examine the effects of the initial stress on the propagation behaviors of SH wave,the dispersion curves of the first mode with different values of the initial stress under“so”and “oo”cases are presented in Fig.3 and 4 respectively,where f=0.1.For the convenience of discussion,we calculate the bulk shear wave velocityand Bleustein-Gulyaev(B-G)surface wave velocityof PZT-5A by using the material constant listed in Table 1,and referring to the original works[Bleustein(1968);Gulyaev(1969)],that is,andIt is found that the phase velocity of the first mode for“so”case approach the velocity of the B-G surface wave of PZT-5A(2000 m/s)with the increase of wave number when the initial stress is equal to zero.However,for“oo”case,the phase velocities tend to the bulk shear wave velocity of PZT-5A(2264.9 m/s).The effect of initial stress on phase velocity becomes very strong with the increase of the wave number.It is also found that the positive initial stresses make the wave velocity increasing,while the negative initial stresses decrease the wave velocity.Moreover,the larger the absolute values of the initial stress,the larger the degrees of increase(induced by compressive stress)or decrease(induced by tensile stress)of the phase velocity.

Figure 3:Influence of initial stress on the first mode for“so”case

Figure 4:Influence of initial stress on the first mode for“oo”case

5.3 Effect of the thickness ratios

The dispersion curves of the first mode with different values of thickness ratio under“so”and “oo”cases are shown in Fig.5 and 6,respectively.It is clear that the thickness ratio has great effect on the phase velocity,especially in the smaller wave number.Moreover,it is found that the smaller the thickness ratio is,the larger the phase velocity of the SH wave propagating in the layered structure.The effect of the thickness ratio on the phase velocity gradually disappears with the wave number increasing.

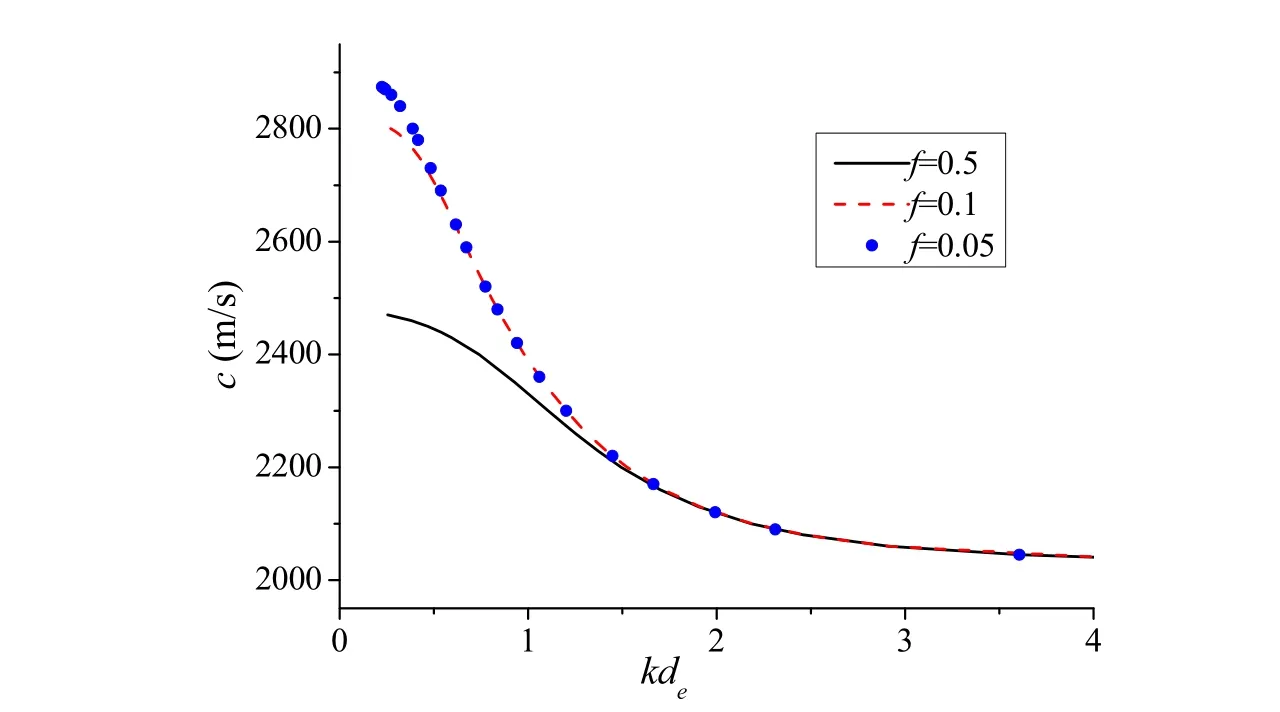
Figure 5:Influence of thickness ratio on the first mode for“so”case

Figure 6:Influence of thickness ratio on the first mode for“oo”case

6 Conclusions

In this paper,we present a theoretical research on the propagation of SH-type guided waves in a piezoelectric/piezomagnetic layered structure with an invariant initial stress.The dispersion relations are obtained under four sets of different electromagnetic boundary conditions.From the numerical results,the following conclusions can be drawn:

a)The dispersion characteristics of the SH-type guided waves are controlled by the electrical boundary conditions and the effect of the magnetic boundary conditions can be neglected.Moreover,the phase velocities of the electrically shorted conditions are smaller than electrically open cases.

b)The positive(compressive)initial stresses make the wave velocity increasing,while the negative(tensile)initial stresses decrease the wave velocity.It is due to the fact that the preloaded compressive stress reinforces the rigidity of the bilayered structure,and the tensile stress is reverse action.

c)The effect of the thickness ratio on the phase velocity is quite obvious in the smaller wave number.

Acknowledgement:This work is supported by the National Nature Science Foundation of China(11272221,10972147),and the Natural Science Foundation of Hebei Province of China(A2013210106).

Bleustein,J.L.(1968):A new surface wave in piezoelectric materials.Applied Physics Letters,vol.13,pp.412-414.

Calas,H.;Otero,J.A.;Rodríguez-Ramos,R.;Monsivais,G.;Stern,C.(2008):Dispersion relations for SH wave in magneto-electro-elastic heterostructures.International Journal of Solids and Structures,vol.45,pp.5356-5367.

Du,J.;Jin,X.;Wang,J.(2007):Love wave propagation in layered magnetoelectro-elastic structures with initial stress.Acta Mechanica,vol.192,pp.169-189.

Du,J.K.;Jin,X.Y.;Wang,J.(2008):Love wave propagation in layered magnetoelectro-elastic structures.Science in China Series G:Physics,Mechanics and Astronomy,vol.51,pp.617-631.

Duan,Y.C.;Zhang,X.M.;Wang,Y.Q.;Yu,J.G.(2014):Wave propagation in functionally graded piezoelectric-piezomagnetic rectangular rings.CMCComputers,Materials,&Continua,vol.43,pp.153-173.

Fiebig,M.(2005):Revival of the magnetoelectric effect.Journal of Physics D Applied Physics,vol.38,pp.R123-R152.

Gulyaev,Y.V.(1969):Electroacoustic surface waves in solids.Soviet Journal of Experimental and Theoretical Physics Letters,vol.9,pp.37-38.

Liu,J.X.;Fang,D.N.;Wei,W.Y.;Zhao,X.F.(2008):Love waves in layered piezoelectric/piezomagnetic structures.Journal of Sound and Vibration,vol.315,pp.146-156.

Liu,J.X.;Wei,W.Y.;Fang,D.N.(2010):Propagation behaviors of shear horizontal waves in piezoelectric-piezomagnetic periodically layered structures.Acta Mechanica Solida Sinica,vol.23,pp.77-84.

Luan,G.D.;Zhang,J.D.;Wang,R.Q.(2005):Transducer piezoelectric and arrays(Revised edition),Peking University Press,Beijing.(in Chinese)

Mori,K.;Narita,F.;Shindo,Y.(2011):Effect of electric field on the response of clamped-free magnetostrictive/piezoelectric/magnetostrictive laminates.CMCComputers,Materials,&Continua,vol.23,pp.187-199.

Nan,C.W.;Bichurin,M.I.;Dong,S.X.;Viehland,D.;Srinivasan,G.(2008):Multiferroic magnetoelectric composites:Historical perspective,status,and future directions.Journal of Applied Physics,vol.103,pp.031101.

Nie,G.Q.;Liu,J.X.;Fang,X.Q.;An,Z.J.(2012):Shear horizontal(SH)waves propagating in piezoelectric-piezomagnetic bilayer system with an imperfect interface.Acta Mechanica,vol.223,pp.1999-2009.

Qian,Z.;Jin,F.;Wang,Z.;Kishimoto,K.(2004):Love waves propagation in a piezoelectric layered structure with initial stresses.Acta Mechanica,vol.171,pp.41-57.

Soh,A.K.;Liu,J.X.(2006):Interfacial shear horizontal waves in a piezoelectricpiezomagnetic bi-material.Philosophical Magazine Letters,vol.86,pp.31-35.

Wang,B.L.;Mai,Y.W.;Niraula,O.P.(2007):A horizontal shear surface wave in magnetoelectroelastic materials.Philosophical Magazine Letters,vol.87,pp.53-58.

Wei,W.Y.;Liu,J.X.;Fang,D.N.(2009):Existence of shear horizontal surface waves in a magneto-electro-elastic material.Chinese Physics Letters,vol.26,pp.104301.

Zakharenko,A.A.(2013):Piezoelectromagnetic SH-SAWs:A review.Canadian Journal of Pure and Applied Sciences,vol.7,pp.2227-2240.

Zhang,J.;Shen,Y.P.;Du,J.K.(2008):The effect of inhomogeneous initial stress on Love wave propagation in layered magneto-electro-elastic structures.S-mart Materials and Structures,vol.17,pp.507-514.

Zhang,R.;Pang,Y.;Feng,W.J.(2014):Propagation of Rayleigh waves in a magneto-electro-elastic half-space with initial stress.Mechanics of Advanced Materials and Structures,vol.21,pp.538-543.

Zhou,Y.Y.;Lü,C.F.;Chen,W.Q.(2012):Bulk wave propagation in layered piezomagnetic/piezoelectric plates with initial stresses or interface imperfections.Composite Structures,vol.94,pp.2736-2745.

1Department of Engineering Mechanics,Shijiazhuang Tiedao University,Shijiazhuang 050043,China

2Corresponding author.Tel.:+86-311-87935021;E-mail:niegq@stdu.edu.cn.