多跳频信号波达方向与极化状态联合估计算法
2015-12-13张东伟齐子森侯文林
张东伟 郭 英 齐子森 侯文林 张 波 李 教
1 引言
跳频(Frequency Hopping, FH)通信因其优越的抗干扰、抗截获和多址组网等能力,在军事通信系统及各式民用信息系统中得到了广泛应用[1]。对FH侦察的研究一直是通信侦察和无线电频谱监测等领域的热点问题。
针对FH信号的盲检测识别,已有研究主要集中在对载频、跳周期等参数的估计[26]-,较少关注空域信息。而FH信号方位对目标属性识别、跟踪、分选具重要作用。文献[7]利用电磁矢量天线进行FH信号波达方向(Direction Of Arrival, DOA)估计,但最多仅能处理5个信号。文献[8]提出了信源数已知前提下的FH信号DOA估计方法,但要求阵元数大于信源数,且计算量会随着信号数目、跳速的增加成倍增加。文献[9]提出了合作方FH信号DOA估计方法,难以应用于缺少先验信息的侦察环境。文献[10]提出的空时频方法具有良好的信号选择性、干扰和噪声抑制能力,在盲信号分离和线性调频等信号 DOA估计中取得了优于传统方法的性能。文献[11,12]基于空时频处理分别实现了FH信号和跳频/直扩(Frequency Hopping & Direct Sequence, FH/DS)混合扩频信号的DOA欠定估计,但在多信号环境下测向性能易出现“地板效应”。极化是电磁波的重要属性。当多个辐射源的信号特征在时、频、空域中均非常接近以至无法区分时,利用其极化域特征差异仍有可能将其分离。FH信号极化信息结合DOA可有效辅助信号分选、跟踪等。同时,极化信息的引入利于提高阵列的 DOA估计精度。考虑到实际应用中经常出现欠定情况。综上所述,在欠定条件下开展FH信号DOA与极化状态的联合估计具有重要现实意义,但关于该问题的研究鲜有报道。
本文首先利用FH信号各跳的时频聚集性和单源特性,将线性时频分析引入极化敏感阵列信号,推导空间极化短时傅里叶变换(Spatial Polarimetric Short Time Fourier Transform, SPSTFT)矩阵形式;然后基于SPSTFT矩阵和空间极化时频分布(Spatial Polarimetric Time-Frequency Distributions,SPTFD)矩阵,考虑频率碰撞,提出3种不同方法估计FH信号DOA与极化参数;为抑制交叉项,精确定位各跳在时频面上的自项区域,还给出一种高时频聚焦性的FH信号时频分析方法;最后给出了实验仿真数据和性能分析结果。
2 FH信号的极化敏感阵列观察模型
设FH信号 sn( t)的跳周期为Tn,在观测时间Δt内共包含K个跳,第k(k = 1,2,…,K)跳载频为ωnk,起始跳持续时长为Δt0n,则sn(t)可表示为[2]
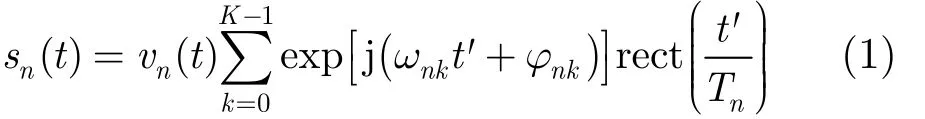
其中,t ' = t - ( k - 1 )Tn-Δt0n,vn( t) 是 sn(t) 的基带复包络,φnk是第k跳的初相,rect( t)为单位矩形窗。
M元极化敏感阵列如图 1所示,阵元间距为d(d < c/2fmax, fmax为侦测频段内FH信号载频最大值),定义坐标原点的阵元为参考阵元。FH信号为宽带信号,如果分析某一跳,可简化为窄带模型。假设极化参数为(γ, η)(γ ∈[0,π/2]为极化辅角,η∈[0,2π]为极化相位差)的窄带平面波信号S以俯仰角 θ ∈ [ 0,π / 2]和方位角 φ ∈ [ 0,2π]沿单位方向矢量-u入射(为简化模型并不失一般性,假定信源位于X-O-Y平面,即θ=90°),则极化矢量表示为[13]
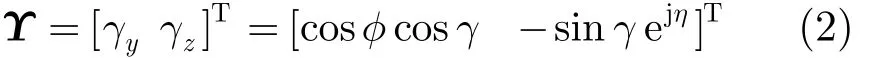
式中,yγ,zγ分别表示沿y, z两个方向的电场分量,上标T表示转置。假设阵列单元增益均为 1,忽略单阵元共点接收通道不一致及互耦影响,阵列对信源S的导向矢量为
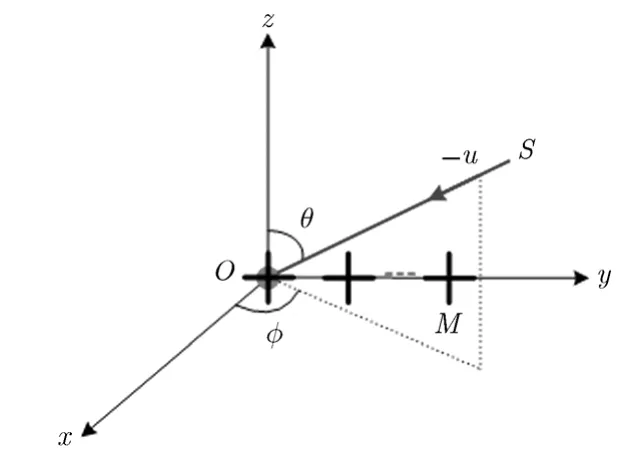
图1 正交偶极子对均匀线阵
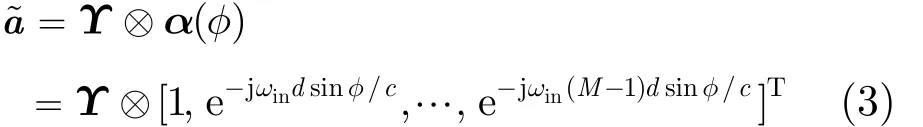
其中,c为光速,ωin为瞬时频率,“⊗”为Kronecker积。若空间存在N个信源 s1~sN,阵列流型矩阵为

则阵列的快拍数据矩阵为
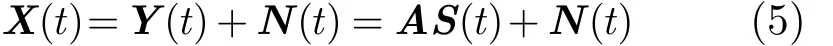
式中,()tS为空间信源的1N×维数据矢量;()tN为阵列的2 1M× 维噪声数据矢量。
3 SPTFD及其线性时频扩展形式SPSTFT
空间极化时频分布(SPTFD)是指将时频分布扩展至极化敏感阵列信号处理。对于信号x1( t)和x2( t),离散时间形式的Cohen类互时频分布为其中,(,)lφτ为核函数。SPTFD矩阵定义为[13]
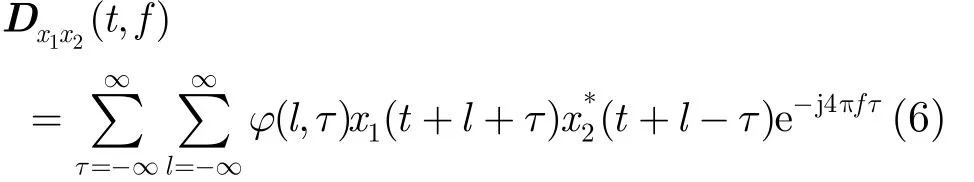
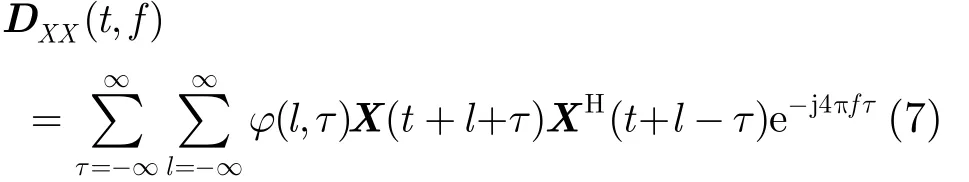
其中,[DXX( t, f) ]ij=Dxixj(t, f) ,i, j = 1,2,… ,2 M 为阵列输出信号间的互时频分布。根据式(5),得时频域阵列协方差模型
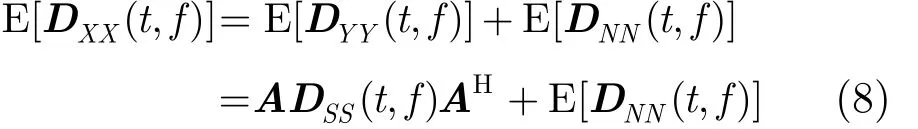
E[DXX(t, f )]与A具有相同的子空间特性。为确保E[DXX(t, f )]满秩,通常选择关注信号的多个自项时频点采取联合对角化或平均处理对其进行估计[13]。
相比于Cohen分布,STFT无交叉项干扰、计算量小,实际中FH信号出现频率碰撞的概率很小,无需借助 SPTFD矩阵子空间多源处理能力,因此在要求快速估计场合,可将Cohen分布用STFT替代。极化敏感阵列信号STFT形式为
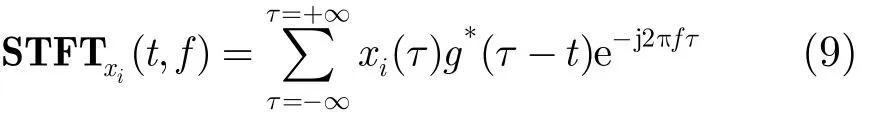
式中, i = y1, y2, … ,yM,z1, z2,… ,zM,g( t) 是时间窗函数。以 S TFTxi(t, f)为元素构造SPSTFT矩阵,有
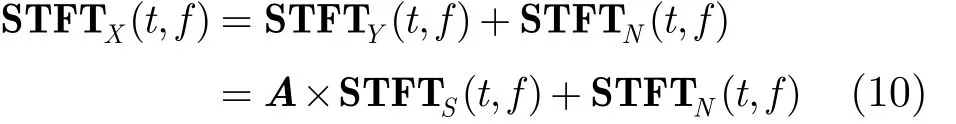
由式(9)可见,构造SPSTFT矩阵的计算量显著低于SPTFD矩阵。
4 DOA与极化参数联合估计
在构造各跳信号的SPTFD/SPSTFT矩阵基础上,利用其蕴含的空-极化域特征信息估计DOA和极化参数。推导中假设:(1)任一时频点对应的信号数小于阵元数(即使出现频率碰撞,该假设也易满足);(2)各FH信号不相关,阵元间噪声不相关。
4.1 基于SPSTFT/SPTFD矩阵和多项式求根的FH信号DOA与极化参数联合估计
方法 1 基于SPSTFT矩阵的估计方法
根据式(10),对于信号 sn第i跳的有效时频点(ta,fa),其SPSTFT矩阵为

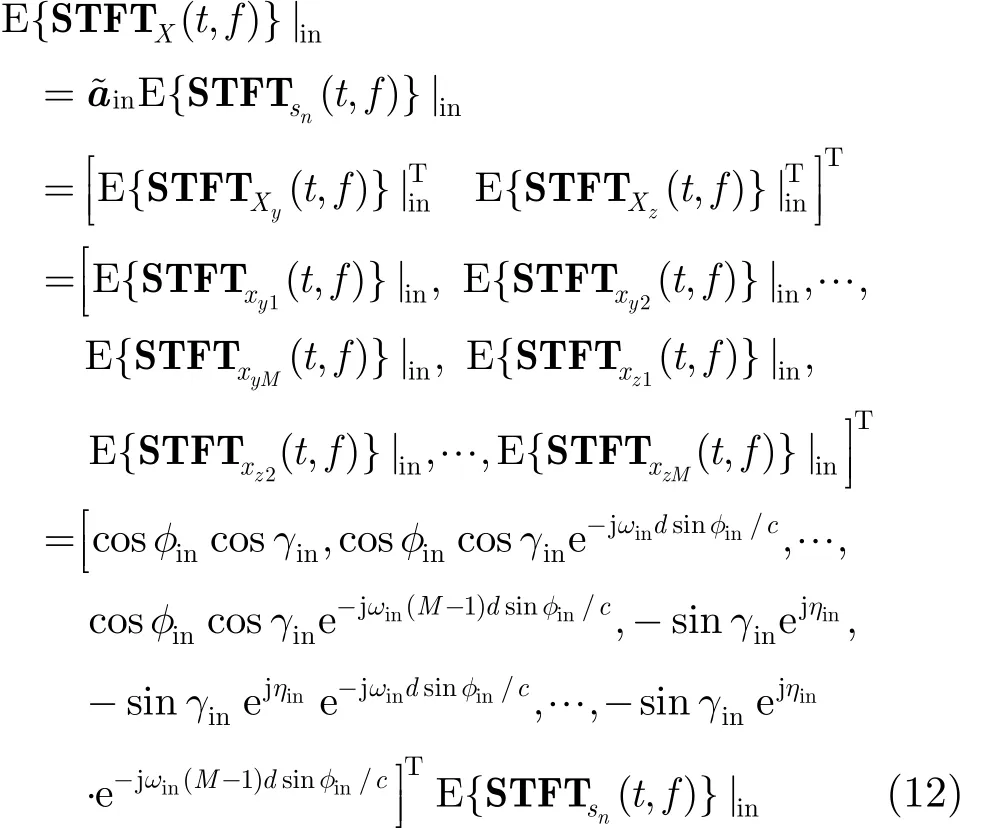
由上式得此跳所在信号DOA与极化参数估计为
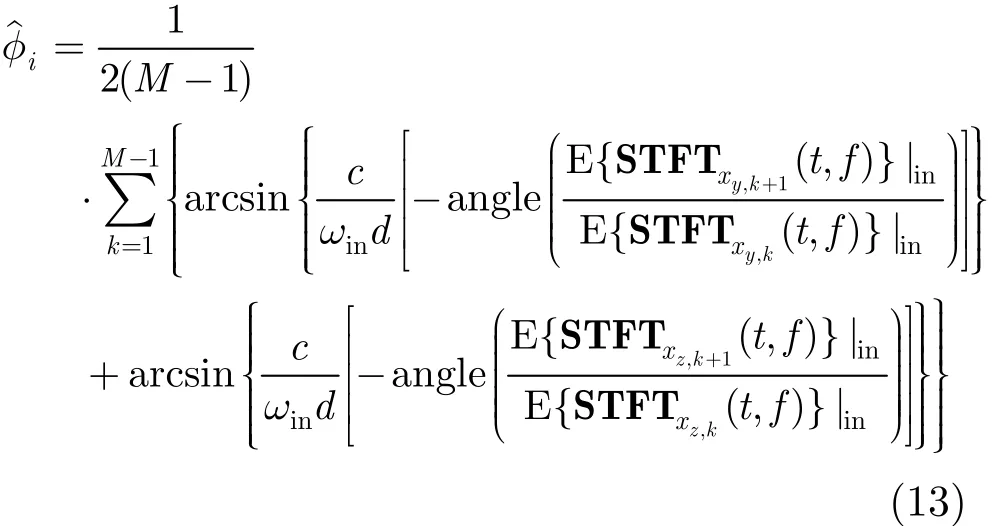
式中,arcsin{}⋅为反正弦函数,angle()⋅表示取相位。
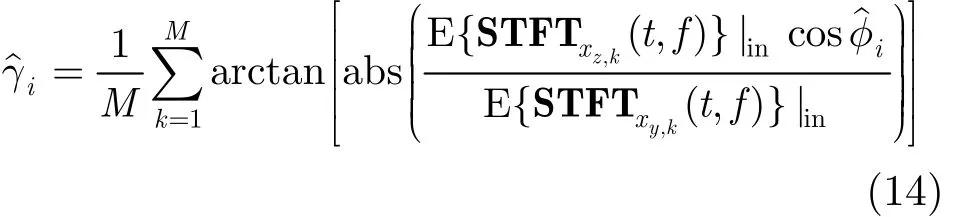
式中,arctan{}⋅为反正切函数,abs()⋅表示取模运算。
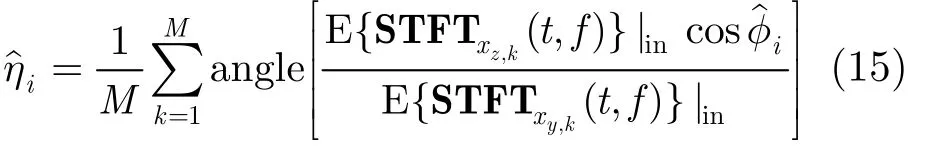
方法 2 基于SPTFD矩阵的估计方法
根据式(8),时频点(ta,fa)的SPTFD矩阵为
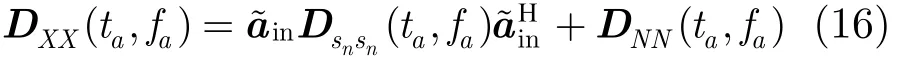
对该跳的全部有效时频点求平均,得到

其中, σ2为噪声方差。令 b =e-jωindsinφi/c,有

分 别 令 Q1=E{ DXyXy(t, f )}|in, Q2=E{ DXyXz(t,f) } |in,Q3=E{DXzXy(t, f )}|in和 Q4=E{ DXzXz(t ,f) } |in,由式(19)得此跳对应FH信号DOA与极化参数估计为


方法 3 基于参数“去耦”和多项式求根的估计方法
当某跳出现频率碰撞的多源情况时,方法1、方法2不再适用(当然,方法3同样适用于无频率碰撞情况)。此时对SPTFD矩阵 E { DXX(t, f)}|in进行特征分解,得到噪声子空间 UN,由子空间原理有

考虑噪声和有限快拍数影响,定义如式(24)所示的优化问题估计信源方位和极化状态
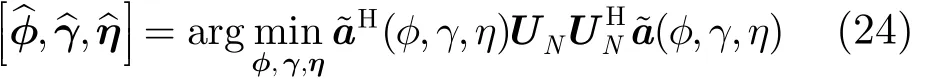
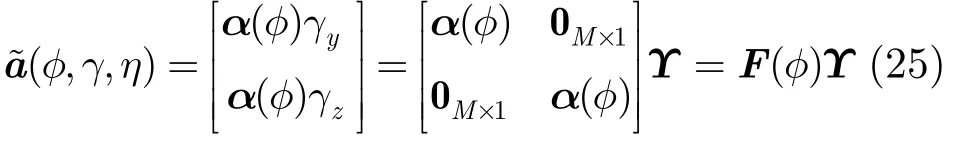
通过式(25)的参数“去耦”,()φF中只包含波程差导致的相位差,而极化参数只包含于Υ中。将式(25)代入式(23)得到
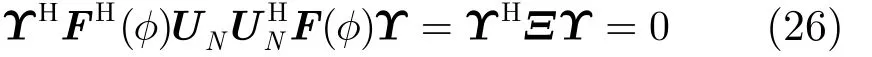
当且仅当φ为信源真实方位时,式(26)成立。由于Υ不全为 0,根据秩损理论[14],可通过 1维角度搜索得到此跳对应FH信号的DOA估计值
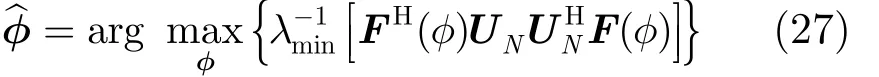
其中, λmin[⋅]为求矩阵最小特征值算子。通过式(27)估计仍需1维搜索,为进一步降低运算量,下面通过多项式求根估计。由式(25)和式(26),有
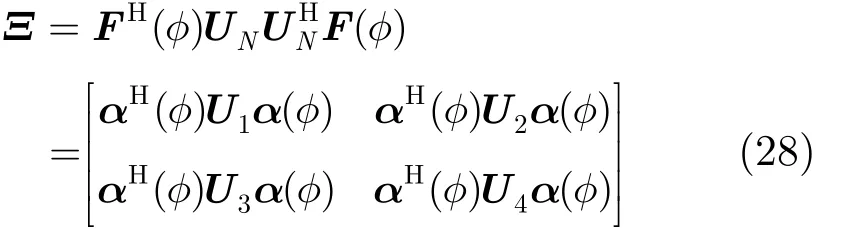
n1n2足UN=[U]T。令 b =e-jωindsinφi/c,重写α(φ)为
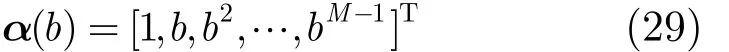
此时,式(27)转换为一个关于b的多项式求根问题,等价为

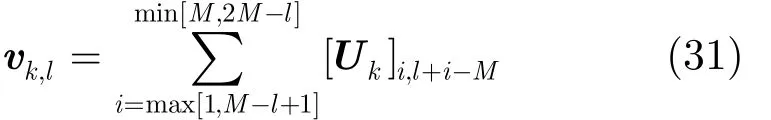
式中, k = 1 ,2,3,4;l = 1,2,… , 2 M -1。因此,多项式m1m4和 m2m3的系数向量 gp,q分别为
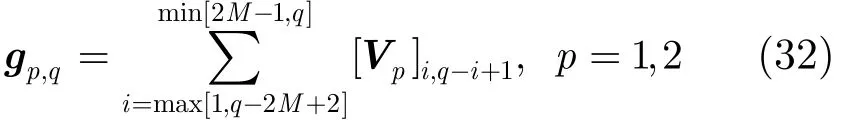
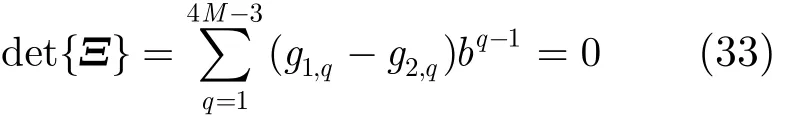
选择式(33)的L个最靠近单位圆不等根用于估计方位角。此时,k =1,2,… ,L 的计算式为
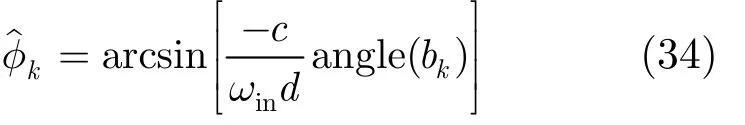
这里kb表示用于估计的一个根。对于每一个,极化矢量估计值为
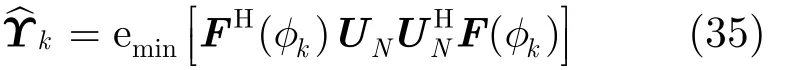
式中,mine[]⋅表示求矩阵最小特征值对应特征矢量算子。因此极化参数估计值为
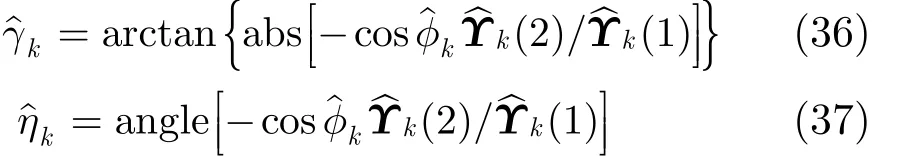
由以上分析可知:
(1)方法1和方法2直接利用SPTFD/SPSTFT矩阵元素估计FH信号参数,计算量很小,利于实时处理。方法3通过参数“去耦”和多项式求根避免了角度搜索和配对,且能处理频率碰撞的跳。
(2)只要空间各FH信号在时频域上存在差异,就可分别构造其SPTFD/SPSTFT矩阵,利用所提方法依次估计各信号参数,从而使阵列系统所能处理的FH信号总数不受阵元数限制。
4.2 FH信号时频分析和SPTFD/SPSTFT矩阵高效构造方法
选取自项时频点构造SPTFD/SPSTFT矩阵是4.1节所提方法估计性能正常发挥的前提。Wigner-Ville分布(WVD)具有最佳的时频聚焦性能,但对FH信号存在严重的交叉项干扰且抗噪性能一般。平滑伪 WVD(Smoothed Pseudo WVD, SPWVD)经过时、频域两次平滑,在交叉项抑制、时频聚焦性和抗噪能力三方面取得了很好平衡。可见,WVD与 SPWVD性能上互为补充。为此,将 WVD和SPWVD组合,使两者的优势均得以保留用于 FH信号分析。将参考阵元的SPWVD, WVD结果分别记为 S PWVDx1x1(t, f ),W VDx1x1(t, f ) 。构造方法为:
步骤 1 将 S PWVDx1x1(t, f ) 与 W VDx1x1(t, f ) 点乘,得到时频模具矩阵 T FMx1x1(t, f),即
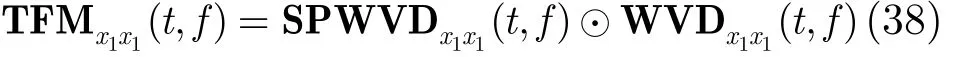
其中,‘⊙’表示Hadamard积。
步骤 2 将 T FMx1x1(t, f ) 进行截断处理得到自项时频地图 T FAx1x1(t, f )并进一步降噪,有

式中,Th为截断门限,计算公式为
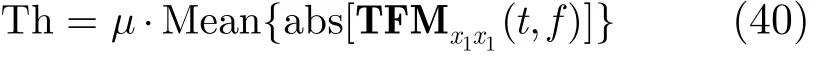
其中,μ为门限因子,Mean{⋅}为取均值算子。
步骤 3 将 T FAx1x1(t, f ) 与 S PWVDx1x1(t, f ) 点乘得到组合时频分布 T FSYx1x1(t, f),为
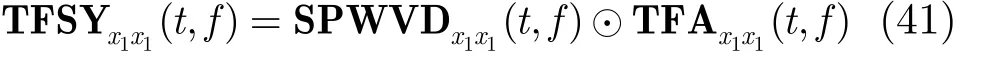
图2为3个FH信号在信噪比5 dB时的WVD,SPWVD和组合时频分布结果。可见,组合时频分布沿袭了WVD时频分辨率,交叉项和噪声也消除殆尽。由式(39)和式(41)知, T FSYx1x1(t, f )中各跳的自项区域为 S PWVDx1x1(t, f )中对应跳的子集,因此,根据参考阵元确定的各跳自项区域提取各阵元时频点构造SPSTFT/SPTFD矩阵。对于SPTFD,时频分布采用与SPWVD性能近似计算量却大为降低的SPW分布。
4.3 多参数联合估计算法步骤
根据以上推导和阐述,可得 FH信号多参数联合估计算法步骤为:
步骤 1 根据式(38)~式(41)对参考阵元快拍数据进行组合时频分布,定位各跳自项时频区域;
步骤 2 估计某跳对应的信源数L,若L大于1,转入步骤6;
步骤 3 选择估计方法,方法 1转入步骤 4,方法2转入步骤5,方法3转入步骤6;
步骤 4 由式(9)构造 SPSTFT 矩阵,根据式(13)~式(15)估计信源参数;
步骤 5 由式(7)构造 SPTFD 矩阵,根据式(20)~式(22)估计信源参数;
步骤 6 由式(7)构造 SPTFD矩阵,对其进行特征值分解得到噪声子空间 UN,求解式(33),选择最靠近单位圆的L个根,根据式(34)~式(37)估计各信源参数;
步骤 7 返回步骤2直至完成所有跳估计。
5 仿真与分析
实验 1 暂无频率碰撞,空间存在FH1, FH2和FH3,为检验各方法性能,同时比较方法1和方法3与文献[12]对应方法的性能差异,用z轴方向短偶极子输出构造各跳的空时频矩阵,得到性能曲线如图3~图7所示。
图3~图7表明,本文所提3种方法对信源方位和极化参数均取得了优异的估计性能:SNR≥4 dB时,方位角RMSE已降至1°以内;SNR≥6 dB时,极化参数RMSE已降至1°以内。由于3种方法原理上都是利用信号与噪声之间的不相关性实现信号与噪声分离,再利用阵列相差完成测向,故3种方法的估计性能差别不大(相比之下,方法3略优于方法1和方法2,主要因为方法3为子空间类方法,具超分辨能力);相对于信源方位,极化参数的RMSE略大,这是因为极化参数的估计误差受噪声和信源方位估计精度的综合影响。
从图3和图6可见,关于DOA估计性能,本文方法1优于文献[12]的线性空时频法,方法3优于文献[12]的二次空时频法。这主要由于本文方法基于双极性阵列展开,相比于文献[12]采用的单极性阵列,阵列流型的空间维度加倍,可供利用的有效信息更多。
实验 2 4个FH信号同时存在,为验证方法3在欠定条件和频率碰撞时的估计性能同时比较方法3与文献[13]算法的性能差异,设定两FH信号发生频率碰撞的概率为1(每次实验随机选择一跳发生碰撞),3个信号以上碰撞概率为0,其余条件与实验1相同,得到性能曲线如图8~图10所示。
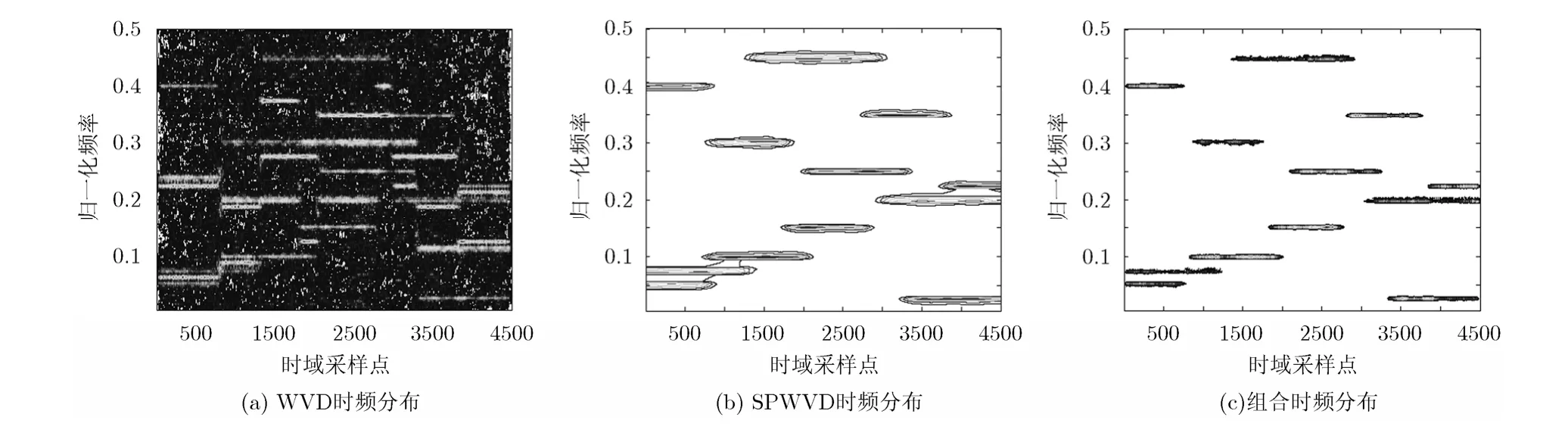
图2 多跳频信号的时频分布结果
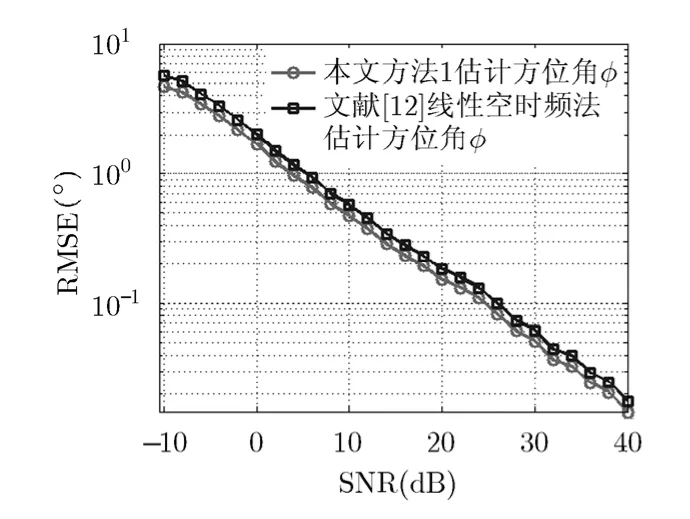
图3 方法1和文献[12]的DOA估计性能
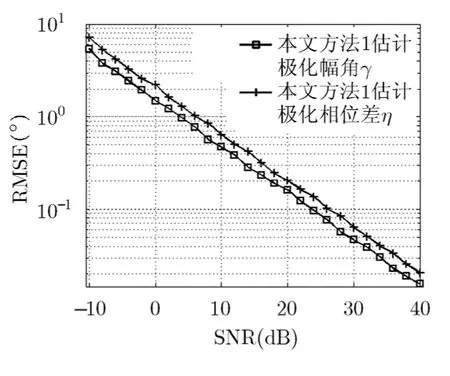
图4 方法1的极化参数估计性能
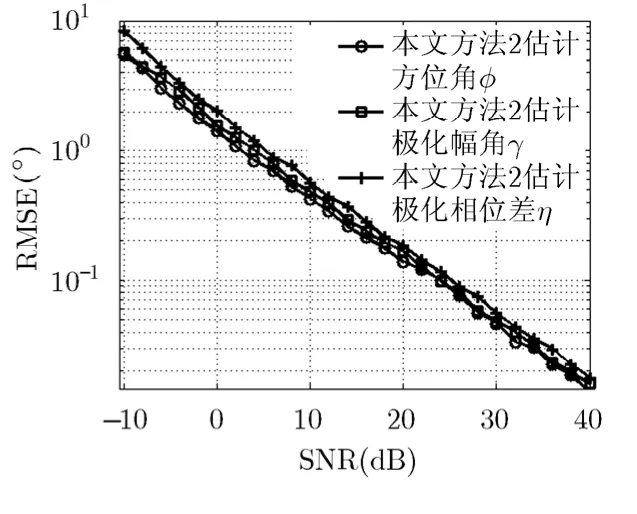
图5 方法2的DOA和极化参数估计性能
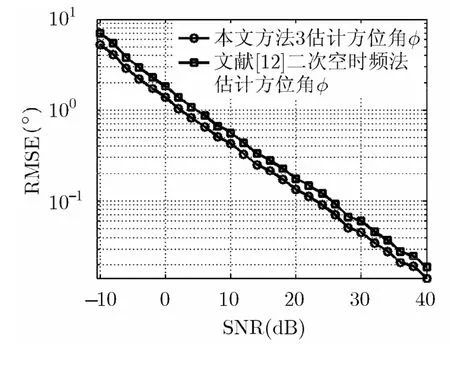
图6 方法3和文献[12]的DOA估计性能
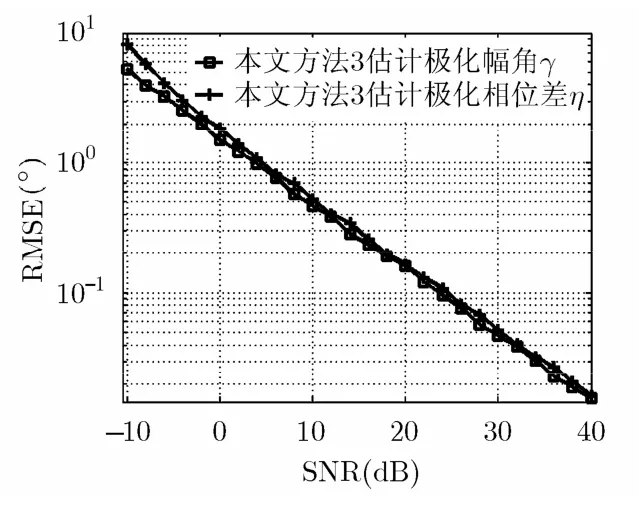
图7 方法3的极化参数估计性能
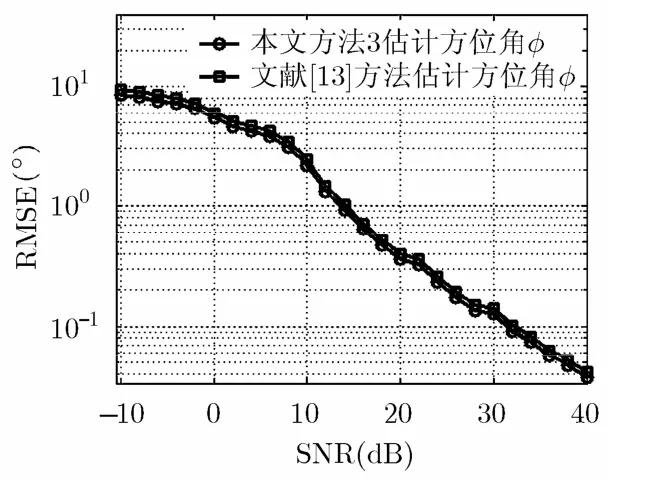
图8 方法3和文献[13]的DOA估计性能
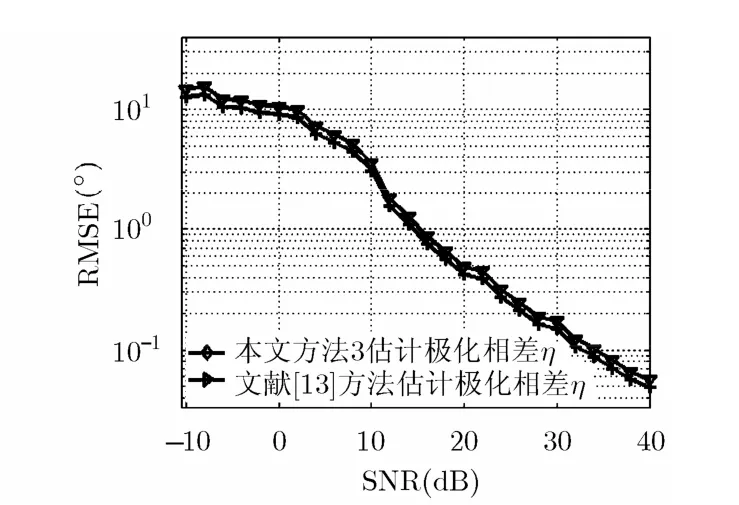
图10 方法3和文献[13]的极化相差估计性能
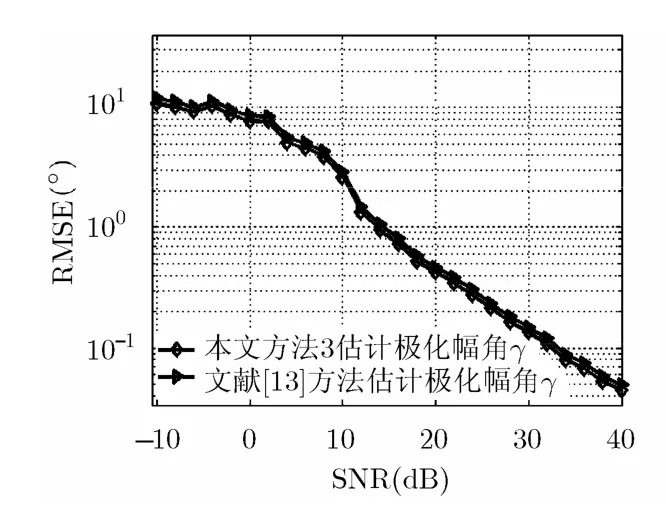
图9 方法3和文献[13]的极化幅角估计性能
由图8~图10可见,在欠定条件和存在频率碰撞时,方法3性能依然良好:SNR>8 dB时RMSE<3°,SNR≥14 dB时RMSE<1°。SNR≤10 dB时,实验 2的估计性能差于实验 1,原因在于:一是频率碰撞时对应跳为多源估计,性能差于无碰撞的单源情况;二是相比于实验1, 4个信号共存在一定程度上加剧了信号间互扰。单看RMSE值,方法3的估计性能稍优于文献[13]中的算法。这主要由于本文采取组合时频分布选取时频点构造 SPTFD矩阵,相比于文献[13]采用的PWVD具有更好的时频聚焦性,即对多信号间互扰具有更好的抑制能力。同时,方法3无需角度搜索。
实验2设定的碰撞概率条件非常苛刻,已远超实际情况,通常两个电台某跳发生频率碰撞已属小概率事件,因此方法3处理频率碰撞情况FH信号多参数估计具有优异性能。实际中可综合考虑处理性能要求(尤其是碰撞跳的分离)与计算量对 3个方法进行灵活选择。
6 结束语
信源方位结合极化信息可有效辅助多跳频网台分选和信号识别、跟踪。实际侦察活动中,空间信源数未知而侦察系统阵元数有限,特别是战时跳频组网密度高,易出现欠定情况。本文详细推导建立了 FH信号的极化敏感阵列快拍数据模型,在此基础上提出3种不同方法实现了FH信号DOA与极化参数的高效联合估计。理论分析和仿真实验表明所提方法可以很好地解决欠定条件和频率碰撞情况下FH信号的多参数联合估计问题。
[1] Sha Zhi-chao, Huang Zhi-tao, Zhou Yi-yu, et al.. Frequencyhopping signals sorting based on underdetermined blind source separation[J]. IET Communications, 2013, 7(14):1456-1464.
[2] 沙志超, 黄知涛, 周一宇, 等. 基于稀疏重构的跳频信号时频分析方法[J]. 通信学报, 2013, 34(5): 107-112.Sha Zhi-chao, Huang Zhi-tao, Zhou Yi-yu, et al.. Time frequency analysis of freqency-hopping signals based on sparse recovery[J]. Journal on Communications, 2013, 34(5):107-112.
[3] Fu Kuo-ching and Chen Yung-fang. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems[J]. IET Communications,2013, 7(9): 883-892.
[4] 王丰华, 沙志超, 刘章孟, 等. 基于贝叶斯稀疏学习的多跳频信号频率跟踪方法[J]. 电子与信息学报, 2013, 35(6):1395-1399.Wang Feng-hua, Sha Zhi-chao, Liu Zhang-meng, et al.. A frequency tracking method for multiple frequency-hopping signals based on sparse bayesian learning[J] Journal of Electronics & Information Technology, 2013, 35(6):1395-1399.
[5] Yang Wen-ge, Li Meng, Wang Li-bin, et al.. Parameter estimation of frequency hopping signals based on time frequency analysis[C]. Proceedings of the 26th Conference of Spacecraft TT&C Technology, Beijing, China, 2013:131-140.
[6] 赵新明, 金艳, 姬红兵. α稳定分布噪声下基于Merid滤波的跳频信号参数估计[J]. 电子与信息学报, 2014, 36(8):1878-1883.Zhao Xin-ming, Jin Yan, and Ji Hong-bing. Parameter estimation of frequency-hopping signals based on Merid filter in α stable noise environment[J]. Journal of Electronics &Information Technology, 2014, 36(8): 1878-1883.
[7] Wong K T. Blind beamforming/geolocation for wideband-FFHs with unknown hop-sequences[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 65-76.
[8] Liu X Q, Nicholas D S, and Swami A. Joint hop timing and frequency estimation for collision resolution in FH networks[J]. IEEE Transactions on Wireless Communications, 2005,4(6): 3063-3074.
[9] Lin C H and Fang W H. Joint angle and delay estimation in frequency hopping systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1042-1056.
[10] Zhang Y M, Mu W F, and Amin M G. Subspace analysis of spatial time-frequency distribution matrices[J]. IEEE Transactions on Signal Processing, 2001, 49(4): 747-759.
[11] 陈利虎. 基于空时频分析的多分量跳频信号DOA估计[J]. 系统工程与电子技术, 2011, 33(12): 2587-2592.Chen Li-hu. Directions of arrival estimation for multicompo nent frequency-hopping signals based on spatial time frequency analysis[J]. Systems Engineering and Electronics,2011, 33(12): 2587-2592.
[12] 陈利虎, 王永明, 张尔扬. 基于空时频分析的多FH/DS信号DOA估计[J]. 信号处理, 2009, 25(8): 1309-1313.Chen Li-hu, Wang Yong-ming, and Zhang Er-yang. Directions of arrival estimation for multicomponent frequency hopping/ direct sequence spread spectrum signals based on spatial time-frequency analysis[J]. Signal Processing, 2009,25(8): 1309-1313.
[13] Zhang Y M, Obeidat B A, and Amin M G. Spatial polarimetric time-frequency distribution for direction-of- arrival estimation[J]. IEEE Transactions on Signal Processing, 2006,54(4): 1327-1340.
[14] 张树银, 郭英, 齐子森. 锥面共形阵列信源方位和极化参数的联合估计算法[J]. 电子与信息学报, 2011, 33(10): 2407-2412.Zhang Shu-yin, Guo Ying, and Qi Zi-sen. Joint estimation of 2D DOA and polarization with conical conformal array antenna[J]. Journal of Electronics & Information Technology,2011, 33(10): 2407-2412.
[15] Xia Tie-qi, Zheng Yi, Wan Qun, et al.. Decoupled estimation of 2-D angles of arrival using two parallel uniform linear arrays[J]. IEEE Transactions on Antennas and Propagation,2007, 55(9): 2627-2632.
