不规则地形地波传播衰减因子的改进算法及结果一致性研究

周丽丽 穆中林 蒲玉蓉 席晓莉

1 引言

低频地波被广泛用于导航授时系统。近年有关低频地波新的研究应用方向主要有：浅水导航、土壤水分探测、新的捕获降噪方法实现等方面[13]-。地波信号在传播过程中受到传播路径的大地电参数、地形起伏及大气折射指数等因素的影响，其传播特性难以精确预测，从而导致该类系统精度降低[47]-。

目前基于均匀光滑路径模型的理论预测方法主要有留数级数法，基于复杂（分段均匀光滑/不均匀不光滑）路径模型的预测方法主要有 Millington方法、Wait积分方法、抛物线方程方法以及积分方程方法等，其中能考虑地形影响的算法主要是积分方程方法[8,9]。其最早由文献[10]1952年基于格林第 2定理提出；1970年文献[11]根据抛物线方程得到的另外一种积分形式；1988年文献[12]则基于补偿原理得到更为一般意义的积分形式。研究表明，这些方法在低频段具有相同的结果[9]。由于能够考虑传播路径实际地形起伏变化和电参数分布，理论上该方法比其它经典算法预测精度更高，且具有普适性。

对于复杂地形路径，目前国内普遍采用的积分方程公式[1317]-与第1种积分公式相同或相近，衰减因子预测结果多是基于此方法。但即使在均匀光滑路径模型下，文献[14,15,17]给出的结果在地面接收距离大于 300 km时会与留数级数法的结果存在较大偏差，且传播距离越远，误差越大，在1700 km的距离上二者预测的传播相位差别甚至高达 16 μs[17]。上述文献中没有给出造成此项误差的原因。

本文针对积分算法与其它经典算法预测结果不一致的问题进行讨论，在对不同路径模型地波衰减因子的定义、物理含义及相关算法公式研究基础上，给出了积分方程算法的推导过程，分析了误差产生原因，并对其进行改进，使之与其它理论算法预测结果趋于一致。下文时间因子统一取 e-jωt。

2 积分方程方法存在问题及算法改进

2.1 典型地面模型下地波衰减因子求解算法

在地波传播理论预测中，当观察点及场源均离地面不远，则观察点处的电场垂直分量可表示为[8,18]

其中

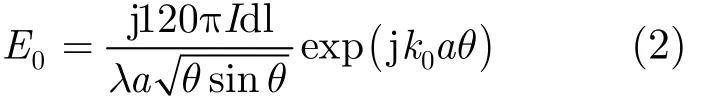
a为等效地球半径，dl为电流元长度，θ为观察点至场源的大圆角距离，Wg称为地波衰减因子，它是传播路径地形及电参数的复杂函数。在实际工程应用中，当已知的是发射台的辐射功率 Pr，以kW计。若传播路径的角距离 θ ≤π/12，则sinθ≈θ,a≈aθ=d,d为大圆距离，如果d以km计，则 E0可表示为

E0物理含义是理想导电平面条件下，场源（垂直电偶极子）及接收点均在地面，且传播距离为d时接收点处电场垂直于地面的分量。

2.1.1 均匀光滑球地面 若地面为均匀光滑球地面，已知地面相对介电常数为εr，电导率为σ，留数级数算法中地波衰减因子Wg可表示为[4,5]

此处

h1和h2分别为发射点和接收点离地面高度，w2（ t）是爱里函数。式中参数q可表示为

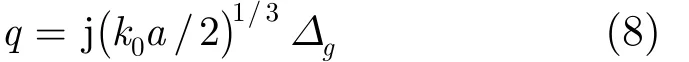
Δg为归一化地表面阻抗，可表示为

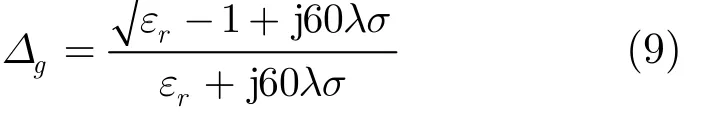
ts是微分方程 w'2（t） - q w2（ t）= 0 的第s个根。

2.1.2 分段均匀光滑球地面 当地面为分段均匀光滑球地面，设从发射点到接收点的传播路径分为 N个有限段，每段长度分别为： d1,d2,…,dN，归一化表面阻抗分别为Δg1,Δg2,…,ΔgN。对应的地波衰减因子求解方法目前主要有 4种：Wait积分法、Millington方法、波模转换法以及抛物线方程方法，下面仅给出抛物线方程方法相关公式。

设电波传播的介质环境沿方位角φ没有变化，且大气折射指数沿高度方向不变，令磁场Hφ=[ε/ （r sin θ）]1/2ejkaθu（ r,θ），进行坐标变换，则可以推出u（ x, z）满足式（10）的抛物线方程[19]：

其满足边界条件

其中

当已知x处地面及空中的u（ x, z），式（10）可以通过分步混合傅里叶变换或有限差分法求解下一段x +Δx 处的任意高度的 u（ x + Δx , z），进而不断迭代得到任意一点的u（ x, z）。再根据式（13）求解出地波衰减因子

其中 H （x, 0） = - jk Id lejkx/2πx 。迭代初值可以由近0距离的平地面公式求解得到。

2.1.3 不均匀不光滑地面 若电波传播路径上地面电导率及地形都有复杂变化，此时地波衰减因子可以用积分方程[4,13]的数值解来求得。记发射源点的位置为O，观察点的位置为P，地面上积分动点为Q，传播路径几何示意图如图1所示。地波衰减因子满足的积分方程为[8,18]

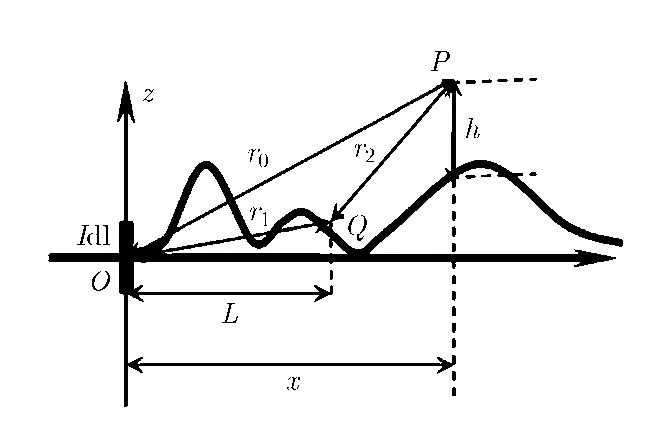
图1 积分方程方法中传播路径几何示意图

其中 r1表示从源点到地面上积分动点Q之间的直线距离，2r表示从Q点到P的距离， h为所在直角坐标系中接收点距离地面的垂直高度。n表示地表面的法线方向。其中x表示观察点至源点水平距离，L是Q与源点之间的水平距离。地面接收时A为1.0，空中接收时A为0.5。

2.2 积分方程方法直接预测地波衰减因子存在问题

由式（1），式（3）和式（13），光滑路径和分段均匀光滑路径模型下相关算法中地波衰减因子实质上是将实际接收点电场的垂直分量或磁场的水平分量与良导体平地面上相应传播距离下场分量归一化的结果，其考虑了近场感应、地球曲率、收发点高度以及地面有限电导率的影响。为分析采用积分方程方法与其它经典算法预测衰减因子不一致的问题，下面简述积分方程方法的推导过程[13,17]。

在一个含有源为垂直电偶子的充满空气的封闭区域V内，电磁场的赫兹势Π满足标量非齐次波动方程

其中J是电流密度矢量，其模用J表示，δ（o）为冲击函数，代表源的分布。取直角坐标系x,y,z,J的方向为z方向。区域V被大地表面与一个半径无穷大的半球面包围（不包含P点），利用第2格林定理

其中，ψ是一个格林函数，定义为

当地形起伏不大，满足z'2≪ 1 （z'为地形函数的一阶导数），根据边界阻抗条件

（其中Δg为归一化地表面阻抗，n为外法线分量），经过一系列计算可以得到

式（19）第1项为源在观察点贡献的直达波，以Π0（P）表示，第2项代表边界上二次源对观察点贡献的场。若地面为一个无限大良导体平面时，可以知道此时P点场为2Π0（P）。此时衰减因子定义为[13,17]

将式（20）代入式（19），可以得出假定地形沿y方向没有变化，应用稳定相位原理及一系列近似，可进一步简化近似为1维积分式（14）。

由式（20）可以看出，积分方程方法中用于求解地波衰减因子的参考场量和以上其它各种方法不同。积分方程方法中参考场量对应的电波传播距离为收发点之间的直线距离，而其他算法中的参考场量对应传播距离为收发两点的地表面上的大圆距离。只有当传播距离很近，且收发点均在地面上时，两种距离才能近似相等。这是积分方程方法与其它算法预测结果不一致的首要原因，由此导致即使在均匀光滑球地面模型下，其地波衰减因子预测结果与留数级数方法存在较大误差。

再者，采用积分方程方法求解空中接收点时，离地高度（如图 1所示）是指直角坐标系下离地垂直方向（z方向）高度，而其它算法中求解高空地波衰减因子（如式（6），式（7）和式（10））算法中对应的高度均是在球坐标系下定义的径向（r方向）离地高度。该问题会进一步造成接收高度越高，与其它理论算法误差越大的现象，且由于空中预测算法中离地高度并非海拔高度，算法对于空中传播预测结果应用于实际工程时难以直接应用，需要进行高程转换。

2.3 积分方程方法改进算法

针对积分方程方法存在的问题，本文提出对积分方法进行如下改进。

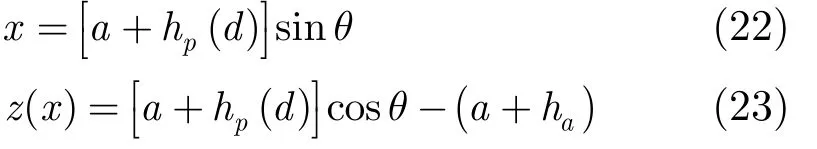
已知传播路径随大圆距离d变化的地形海拔高度 hp（ d），首先将其转换为直角坐标系下的地形函数z（ x） ：其中ha为发射天线处的海拔高度。将z（ x）代入式（14），求解原积分方程，可得到观察点 Wg（ d, h ）（注意此处h和d分别表示原式（14）中大圆距离和接收高度）。

以 Pg表示改进后的衰减因子， hpR表示接收点实际的海拔高度， dp表示改进后对应的大圆距离，则

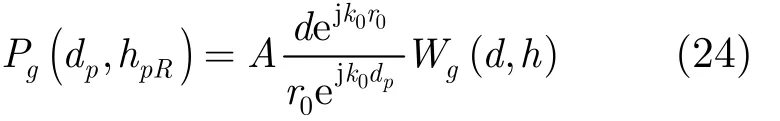
图2 改进算法中地波衰减因子函数变量几何示意

从式（24）可以看出本次算法改进的方式是对原算法求得的直角坐标系中大圆距离为d，离地垂直高度为h处的地波衰减因子，采用球面校正因子和高程转换技术进行校正后得到的实为大圆距离为dp，海拔高度为 hpR处的地波衰减因子。

由上述推导分析可知直角坐标系中相同水平距离下，接收点分别在地面与空中时，在改进算法中对应的大圆距离不同。实际工程应用中当求解相同经纬度，不同海拔高度处的地波衰减因子时，在原积分算法中对应的水平距离或大圆距离也应不同。改进后的积分算法中，衰减因子包含了近场感应、地球曲率、地形起伏、有限电导率以及收发高度因素等对地波传播特性的影响。同时，由于改进后的衰减因子中 hpR是观察点海拔高度，亦更适合工程应用。

3 积分方程改进算法的数值结果验证

该节对积分方程改进算法与其他方法结果的一致性进行了验证。

图3给出了接收高度 hpR分别为0 km和10 km条件下，采用积分方程、留数级数，抛物线方程方法计算的均匀光滑球地面的结果，电参数选择为：σ= 3 × 1 0-3s/m, εr= 1 5。地球半径取等效地球半径 ae= 4 a/3，其中 a = 6 371.12 km。

从图3可以看出，经改进后，积分方程方法结果与其它方法预测结果一致性非常好，均匀光滑地面条件下在1000 km范围内与留数级数法幅度误差小于0.2 dB，相位误差小于50 ns。

图4给出了不同接收高度（0 km, 5 km及10 km）条件下，采用积分方程算法、抛物线方程方法、波模转换法以及Millintong算法计算的陆海两段均匀光滑球地面的结果。其中Millintong算法只适用于地面接收的情况，因此只给出了地面接收结果。第1段路径长 400 km，电参数为： σ = 1 0-3s/m,εr=10。第2段路径长600 km，电参数为：σ=5 s/m, εr= 8 0。地球半径仍取等效地球半径 ae=4a/ 3。

从图4可以看出，分段均匀光滑条件下改进积分方程方法与抛物线方程、波模转换方法预测结果一致性也非常好，Millington算法与其它算法误差略大。

图 5（a）所示的是一条实际复杂传播路径上测量点分布区域图。测量信号为宣城台（O 点所示）播发的导航信号，沿该路径共测量了8个点的相位，其中地面上测量了6个点，海拔为4.26 km的高空测量了1个点，海拔为6.40 km处测量了1个点。图5（b）所示的是沿该路径地形高程及 8个测量点空间位置分布，其中1～6为地面测量点，7, 8为两个空中测量点。采用改进积分方程方法对该路不同高度（地面、4.26 km, 6.40 km）衰减因子相位进行预测，并将预测结果与上述8个点的实测结果进行比较，如图 5（c）所示。该路径中平原地区电参数取σ=3 × 1 0-3s/m, εr= 1 3； 山 区电参 数取 σ = 4 × 10-4s/m, εr= 7 。

图3 均匀光滑球地面条件下地波衰减因子算法一致性验证

图4 分段均匀光滑球地面条件下地波衰减因子算法一致性验证

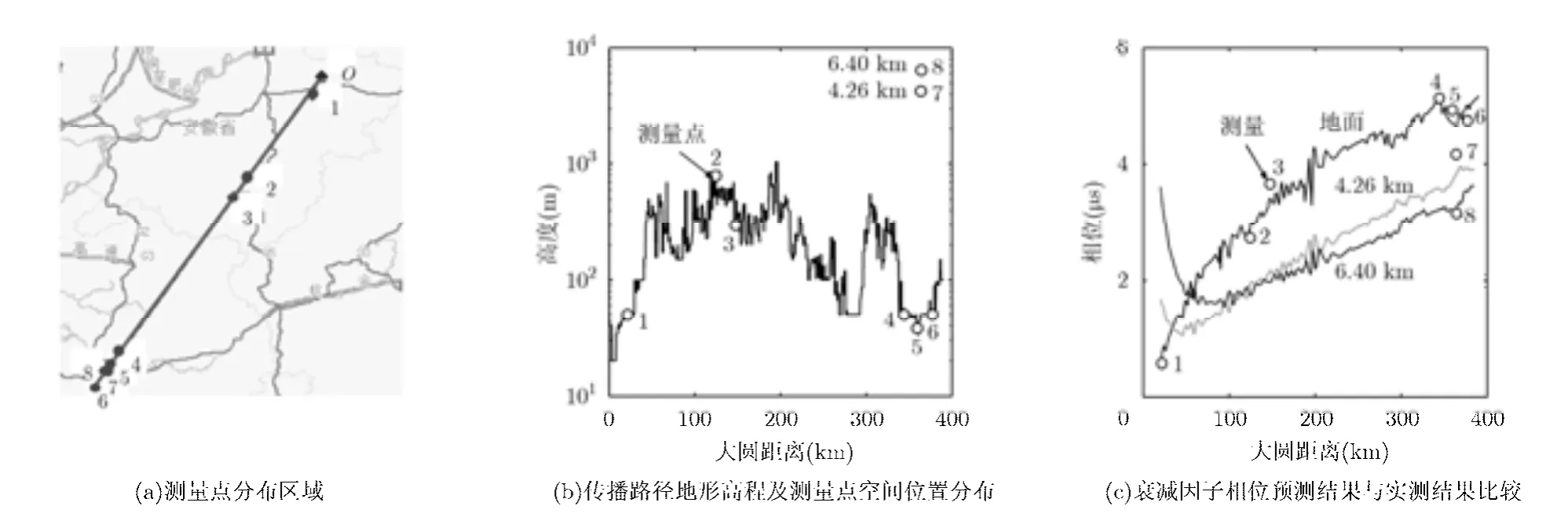
图5 复杂不规则路径积分方程方法预测结果与实测结果比较

从图5看出对于该复杂路径，算法结果与实测结果吻合很好。

4 结束语

本文主要研究了低频地波理论衰减因子算法中预测结果不一致的问题。给出了地波衰减因子预测中积分方程方法的改进公式，使不同算法在均匀/分段均匀光滑路径模型下的地波衰减因子预测结果趋于一致，提高了电波地面长距离传播衰减因子的精度，同时该算法更加适合实际工程问题的求解。受限于积分方程方法的局限性，诸如模型推导近似、数值积分近似及奇点处理等，文中改进算法对于地形起伏较缓的不规则路径预测精度较高。对于地形起伏剧烈的不规则路径，积分方程方法可通过与电磁场数值计算方法相结合等途径进一步提高其预测精度[20]。

[1] Feng Y and Astin I. Remote sensing of soil moisture using the propagation of Loran-C navigation signals[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12（1）:195-198.

[2] Lei W and Chen B. Low complexity sparse noise reduction method for Loran-C skywave delay estimation[J]. Electronics Letters, 2013, 49（24）: 1572-1574.

[3] 李实锋, 王玉林, 华宇, 等. 罗兰-C信号抗干扰的快速检测方法[J]. 西安交通大学学报, 2013, 47（10）: 91-96.Li Shi-feng, Wang Yu-lin, Hua Yu, et al.. A fast anti-interference detection method for Loran-C signal[J].Journal of Xi’an Jiaotong University, 2013, 47（10）: 91-96.

[4] Zhou Li-li, Xi Xiao-li, Zhang Jin-sheng, et al.. A new method for Loran-C ASF calculation over irregular terrain[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013,49（3）: 1738-1744.

[5] Šafař J, Williams P, and Vejražka F. Accuracy performance of e-Loran receivers under cross-rate interference conditions[J]. Annual of Navigation, 2013, 19（1）: 133-148.

[6] 李实锋, 王玉林, 华宇, 等. 罗兰-C信号快速捕获方法及其性能分析[J]. 电子与信息学报, 2013, 35（9）: 2175-2179.Li Shi-feng, Wang Yu-lin, Hua Yu, et al.. Loran-C signal fast acquisition method and its performance analysis[J]. Journal of Electronics & Information Technology, 2013, 35（9）:2175-2179.

[7] Seo J and Kim M. eLoran in Korea - current status and future plans[C]. Proceedings of the European Navigation Conference, Vienna, 2013: 23-27.

[8] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004: 106-173.

[9] Gesny H and Ravard O. Propagation over irregular terrain in the VHF band a review of integral equation models[C].Proceedings of the National Conference on Antennas and Propagation, York, UK, 1999: 61-64.

[10] Hufford G A. An integral equation approach to the problem of wave propagation over an irregular surface[J]. Quarterly Journal of Applied Mathematics, 1952, 9（4）: 391-404.

[11] Ott R H. An alternative integral equation for propagation over irregular terrain, 2[J]. Radio Science, 1971, 6（4）:429-435.

[12] Wu Z, Maclean T, Bagwell D, et al.. Propagation over an inhomogeneous irregular surface[J]. Radio Science, 1988,23（1）: 33-40.

[13] 梁仲寰, 李滨. 山区地形对100 kHz地波相位影响的实验研究[J]. 陕西天文台台刊, 1996, 19（1）: 88-97.Liang Zhong-huan and Li Bin. The experiments on the effects of mountain terrain upon 100 kHz ground wave phase[J].CSAO Publications, 1996, 19（1）: 88-97.

[14] 王东文. 复杂地面条件下低频地波传播的三维预测[J]. 电波科学学报, 1988, 3（1）: 50-63.Wang Dong-wen. Three-dimensional prediction for the propagation of low-frequency groundwave over inhomogeneous irregular terrain[J]. Chinese Journal of Radio Science, 1988, 3（1）: 50-53.

[15] 温芳茹. 地形对地波衰减因子的影响[J]. 电波科学学报, 1987,2（1）: 27-38.Wen Fang-ru. The effect of the terrain on the groundwave attenuation factor[J]. Chinese Journal of Radio Science, 1987,2（1）: 27-38.

[16] 彭怀云, 樊文生, 潘威炎, 等. 沿不规则不均匀地面传播的侧面波[J]. 电波科学学报, 2006, 21（4）: 497-502.Peng Huai-yun, Fan Wen-sheng, Pan Wei-yan, et al.. Lateral wave propagation along irregular and inhomogeneous ground[J]. Chinese Journal of Radio Science, 2006, 21（4）: 497-502.

[17] 陈秀明. 罗兰C组合导航中地波ASF修正研究[D]. [硕士论文],中国科学院, 2007.Chen Xiu-ming. Study on ASF corrections in integrated navigation systems of Loran-C[D]. [Master dissertation],Chinese Academy of Sciences, 2007.

[18] 熊皓. 无线电波传播[M]. 北京: 电子工业出版社, 2000:331-363.

[19] 潘威炎, 彭怀云, 张红旗. 非均匀光滑球面地波衰减因子的抛物方程算法[J]. 电波科学学报, 2006, 21（1）: 37-42.Pan Wei-yan, Peng Huai-yun, and Zhang Hong-qi. Parabolic equation algorithm of wave attenuation along inhomogeneous smooth ground[J]. Chinese Journal of Radio Science, 2006,21（1）: 37-42.

[20] Xi X, Zhou L, Zhang J, et al.. Combined IE-FDTD algorithm for long-range Loran-C ground-wave propagation[J]. IEEE Transactions on Antennas and Propagation, 2012, 60（8）:3802-3808.