D-T2二维核磁共振技术发展综述
2015-12-13吴飞范宜仁李进邓少贵邢东辉巫振观杨培强
吴飞,范宜仁,李进,邓少贵,邢东辉,巫振观,杨培强
(1.中国石油大学(华东)地球科学与技术学院,山东 青岛266580;2.中国石油大学CNPC测井重点实验室,山东 青岛266580;3.中国石油渤海钻探工程有限公司测井分公司,天津300280;4.上海纽迈电子科技有限公司,上海200333)
0 引 言
核磁共振技术凭借快速、无损、无侵入、无毒、只对含氢孔隙流体敏感等优点,从20世纪50年代开始被引入到石油勘探领域[1-5]。自20世纪90年代初首支脉冲核磁共振测井仪器投入商业服务以来,基于CPMG脉冲序列的一维核磁共振技术步入高速发展期,在孔隙度、渗透率、饱和度计算,孔隙结构评价,流体识别等方面得到成功应用,为储层评价和产能预测提供了重要信息[6-30]。由于一维T2谱油气水信号的重叠,而差谱法(DSM)、时域法(TDA)、移谱法(SSM)、扩散分析法(DIFAN)、增强扩散法(EDM)都有局限性[31-37],严重影响了核磁共振测井技术的应用效果[38-39]。
为弥补一维T2谱油气水信号重叠的短板,2002年,Sun和 Dunn[40-41]、Hürlimann等[42-44]、Song等[45]首次将核磁共振波谱学中的二维核磁共振概念应用到石油测井领域,开创了以D-T2、T1-T2为典型代表的二维核磁共振测井方法及岩心分析技术,其中T1-T2主要用于识别气层,D-T2识别油水的效果优于T1-T2,因此D-T2应用较广[46]。经过多年发展,D-T2二维核磁共振技术日趋完善,拓宽了核磁共振测井的应用范围,提高了储层测井解释评价精度[47-51]。
中国D-T2二维核磁共振技术的起步比国外稍晚,受硬件条件制约,目前的研究重点主要集中在D-T2二维核磁共振技术的理论基础研究和现场应用[39,52-62],缺乏对D-T2二维核磁共振技术未来 发展方向的前瞻性把握。鉴于此,本文在简述D-T2二维核磁共振基本原理的基础上,综述D-T2二维核磁共振核心技术D-T2脉冲序列、D-T2数据反演方法的发展现状。综合对比分析基于脉冲梯度场的PFG、STE-PFG、BP-PFG脉冲序列,基于恒定梯度场的改良式CPMG、扩散编程、多回波间隔CPMG序列的优缺点,叙述D-T2数据二维反演方法和一维反演方法基本原理,并举例对比它们的优缺点,为D-T2二维核磁共振技术的未来发展指明方向。
1 D-T2二维核磁共振基本原理
由孔隙介质核磁共振弛豫理论可知,孔隙流体的横向弛豫机制包括自由弛豫、表面弛豫、扩散弛豫[46],即
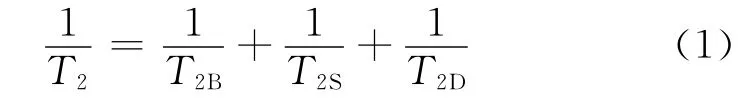
式中,T2是孔隙流体的横向弛豫时间;T2B是横向自由弛豫时间;T2S是横向表面弛豫时间;T2D是横向扩散弛豫时间。
自由弛豫,也称体弛豫,是流体本身的核磁共振弛豫性质,它由流体的物理性质(黏度、化学成分等)决定,同时还受温度、压力等环境因素的影响。
表面弛豫是孔隙中的流体分子与固体颗粒表面不断碰撞造成能量衰减的过程,其表达式为

式中,ρ2是岩石横向表面弛豫强度;S/V是岩石比表面积。
存在固定磁场梯度时,分子扩散引起的增强横向弛豫速率称为扩散弛豫,其表达式为

式中,D是流体的扩散系数;γ是氢核的旋磁比;G是磁场梯度;TE是CPMG脉冲序列的回波间隔。
储层孔隙中的多相流体受自由弛豫、表面弛豫、扩散弛豫的综合作用,一维T2谱往往发生重叠(见图1)。为了准确识别储层流体类型,需要引入表征孔隙流体性质的另一个参数形成二维判别法。为此,测井分析学家引入了核磁共振波谱学中的二维核磁共振概念,但研究对象和属性参数不同。二维核磁共振测井研究的是储层岩石,属性参数是纵向弛豫时间T1、横向弛豫时间T2和流体扩散系数D,而不是微观分子的化学位移[39]。得益于油气水扩散系数的明显差异(一般Dg>
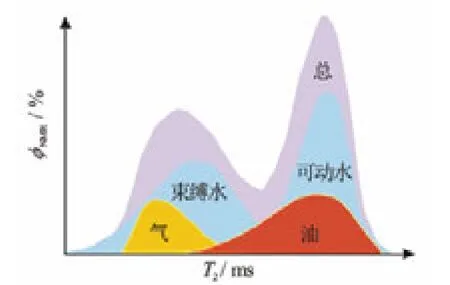
图1 油气水T2谱重叠示意图
Dw>Do),D-T2二维分布能够有效区分油气水(见图2)。当核磁共振测量的等待时间TW足够长时,
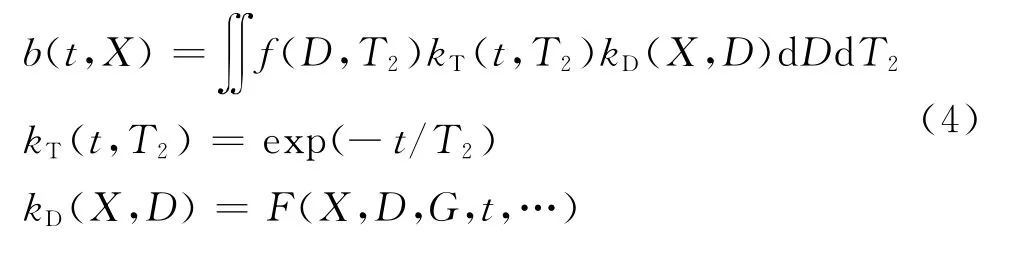
梯度场下自旋回波的幅度可表示为式中,b是回波幅度;T2是孔隙流体的固有弛豫(自由弛豫+表面弛豫),本文中的T2如无特殊说明均指固有弛豫;f(D,T2)是氢核在(D,T2)二维空间的分布;kT是与横向弛豫时间相关的核函数;t是回波时间;kD是与扩散系数相关的核函数;X是加载扩散弛豫的变量。

图2 油气水D-T2分布示意图
选定梯度磁场类型(脉冲梯度、恒定梯度)后,确定扩散弛豫加载变量,设计相应的脉冲序列,实现D-T2二维核磁共振数据采集,开发对应的解谱方法,就能获取储层孔隙流体的D-T2二维分布,用于储层流体识别和饱和度计算。
2 D-T2脉冲序列分类及对比
2.1 脉冲梯度场
脉冲梯度场D-T2测量仪器的特点:用于极化氢核的主磁场是均匀磁场,使用特制的梯度线圈给样品测试区域施加短时脉冲梯度磁场,通过变化梯度电流的大小和持续时间调节脉冲梯度输出,脉冲梯度技术已在高场核磁共振仪器中发展成熟。脉冲梯度场D-T2脉冲序列主要从自扩散系数测定方法发展演变而来,其中最传统的是PFG、STE-PFG脉冲序列;针对特殊用途又在PFG、STE-PFG基础上发展 了 BP-PFG(Bi-polar pulsed filed gradient)、MSE-PFG(Multi-spin echo pulsed filed gradient)、LED-PFG(Longitudinal eddy decay pulsed filed gradient)、DMSE-PFG (Double multi-spin echo pulsed filed gradient)脉冲序列[63-78]。本文着重介绍最常用的PFG、STE-PFG、BP-PFG脉冲序列。
2.1.1 PFG脉冲序列
射频场采集时序的时间轴分为2个窗口,第1个窗口只有1个自旋回波,持续时间为t0,在该窗口内180°脉冲两侧施加1组对称的脉冲梯度,用于加载孔隙流体扩散弛豫信息;第2个窗口用最短回波间隔采集CPMG回波串,采集孔隙流体横向弛豫信息,并且将第1个窗口内的扩散弛豫衰减记录到第2个窗口采集的回波幅度中,为反演获取孔隙流体扩散系数创造条件(见图3)。
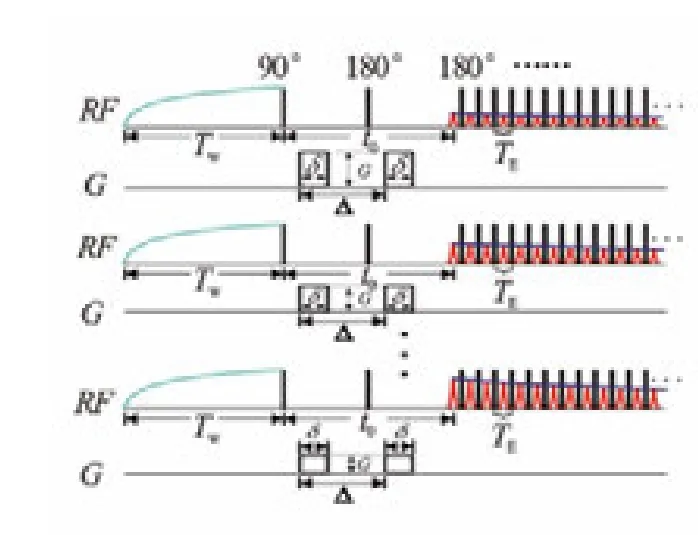
图3 PFG脉冲序列示意图[63]
PFG脉冲序列的回波幅度为
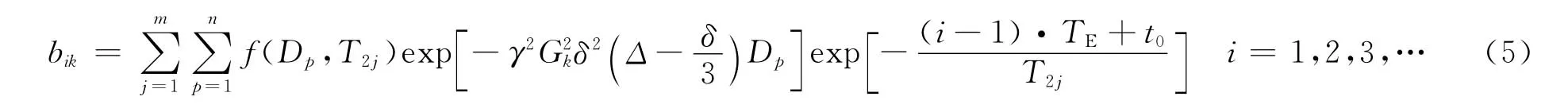
式中,bik代表脉冲梯度为Gk时第i个回波的幅度;f(Dp,T2j)为扩散系数Dp、横向弛豫时间T2j对应的孔隙度分量;γ为氢核的旋磁比;δ为梯度脉冲持续时间;Δ为2个梯度脉冲间的间隔;TE为后续CPMG序列的回波间隔;t0为梯度窗口长度。改变脉冲输出梯度,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(5)联合反演,即可得到储层岩石孔隙流体的D-T2分布,纽迈公司核磁共振岩心分析仪MR-DF的D-T2采集就是采用的该序列。
2.1.2 STE-PFG脉冲序列
将PFG脉冲序列的第1个180°脉冲替换为2个90°脉冲,对称脉冲梯度施加在第1个和第2个90°脉冲、第3个90°脉冲和第1个180°脉冲之间,其余的与图3的PFG序列相同(见图4)。

图4 STE-PFG脉冲序列示意图[65]
由于在第2个和第3个90°脉冲之间的核磁共振信号衰减为纵向弛豫,因此STE-PFG脉冲序列的回波幅度为

式中,bik代表脉冲梯度为Gk时第i个回波的幅度;f(T1q,Dp,T2j)为纵向弛豫时间T1q、扩散系数Dp、横向弛豫时间T2j对应的孔隙度分量;δ为梯度脉冲持续时间;Δ为2个梯度脉冲间的间隔;TE为后续CPMG序列的回波间隔;t1为第2个90°和第3个90°脉冲之间的间隔,即纵向弛豫的时间;t0为第1个窗口中横向弛豫的时间。
当测量对象满足T1≫T2时,式(6)中的纵向弛豫因子exp(-t1/T1)≈1,此时STE-PFG脉冲序列的回波信号衰减可表示为式(5)[65];改变脉冲输出梯度,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(5)联合反演,即可得到储层岩石孔隙流体的D-T2分布,牛津仪器公司岩心分析仪GeoSpec2的D-T2采集就是采用的该序列。
当测量对象中含有短弛豫组分时(T2<t0),由式(5)可知,使用PFG脉冲序列时,梯度作用窗口内短弛豫组分信号衰减过大,其信号可能湮没在后续CPMG回波串的噪声中,导致D-T2反演谱中短弛豫组分的低估,甚至缺失;而STE-PFG脉冲序列则克服了这一局限,通过增大t1、减小t0的方式,在保证扩散弛豫信息有效加载的前提下,减小了梯度作用窗口内短弛豫组分的横向弛豫衰减,不过STE-PFG的适用条件是T1≫T2。对比式(5)、式(6)可知,在t0、G、δ相同时,由于STE-PFG增加了持续时间为t1的纵向弛豫窗口,STE-PFG的扩散弛豫加载时间Δ比PFG大,因此STE-PFG的扩散系数测量范围比PFG大。
2.1.3 BP-PFG脉冲序列
在STE-PFG脉冲序列基础上,将第1个窗口中横向弛豫时间进一步划分,脉冲梯度也增加到2对,2对梯度脉冲的方向相反,其余的与图4的STE-PFG序列相同(见图5)。

图5 BP-PFG脉冲序列示意图[67]
BP-PFG脉冲序列的双梯度设计主要用于克服储层岩石的内部磁场梯度,因此考虑内部磁场梯度g0时,BP-PFG脉冲序列的回波幅度为
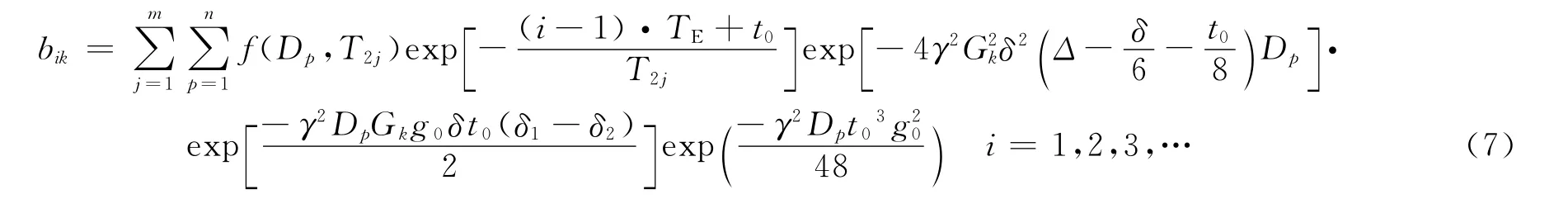
式中,δ1为STE-PFG序列中脉冲梯度距离左侧紧邻扳转脉冲的时间间隔;δ2是脉冲梯度距离右侧紧邻扳转脉冲的时间间隔;g0为岩石内部磁场梯度。
对比式(6)、式(7)、式(8)可知,由于内部磁场梯度的作用,回波串幅度衰减增加了2个与g0有关的增强弛豫因子E(Gg0)、E(g20)。在t0、t1、G、δ相同时,BP-PFG脉冲序列通过设置δ1=δ2,使E(Gg0)=1,与之相对,STE-PFG脉冲序列的E(Gg0)<1,
式中,bik代表脉冲梯度为Gk时第i个回波的幅度;δ为梯度脉冲持续时间,δ1为脉冲梯度距离左侧紧邻扳转脉冲的时间间隔;δ2是脉冲梯度距离右侧紧邻扳转脉冲的时间间隔;Δ为同向脉冲梯度间的间隔;TE为后续CPMG序列的回波间隔;t1为第2个90°和第3个90°脉冲之间的间隔,即纵向弛豫时间;t0为第1个窗口中横向弛豫的时间;g0为岩石内部磁场梯度。

考虑内部磁场梯度g0时,STE-PFG脉冲序列的回波幅度为并且STE-PFG的E(g20)<BP-PFG的E(g20),因此BP-PFG的双脉冲设计有效降低了岩石内部磁场梯度对D-T2数据采集的影响。
由于BP-PFG脉冲序列的独特设计,反演时可忽略内部磁场梯度的影响,则BP-PFG脉冲序列的回波幅度为

改变脉冲输出梯度,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(9)联合反演,即可得到储层岩石孔隙流体的D-T2分布。曲岩涛等[79]在自主研制的低场核磁岩心分析仪上,利用BP-PFG脉冲序列研究了水驱油过程中的油水分布规律。
2.2 恒定梯度场
恒定梯度场D-T2测量仪器的特点:用于极化氢核的主磁场是非均匀磁场,并且磁场梯度大小恒定,或者在某一测量区域内梯度大小恒定,如Halliburton公司的核磁共振成像测井仪 MRIL(Magnetic Resonance Imaging Logging)、Baker Atlas公司的核磁共振探测仪MREX(Magnetic Resonance Expert)和Schlumberger公司的核磁公司扫描仪MR Scanner(Magnetic Resonance Scanner)[46]。恒定梯度场D-T2脉冲序列主要包括改良式CPMG、扩散编程、多回波间隔CPMG脉冲序列。
2.2.1 改良式CPMG脉冲序列
利用分割时间轴的思想,每条CPMG序列的射频场采集时序分为2个窗口,第1个窗口长度固定为t0,改变第1个窗口中的回波个数NE1使回波间隔从大变小,加载储层孔隙流体扩散弛豫信息;第2个窗口用仪器的最短回波间隔采集CPMG回波信号,将扩散弛豫影响降到最小,采集储层孔隙流体横向弛豫信息,同时将第1个窗口中由扩散弛豫引起的衰减记录到第2个窗口采集的回波幅度中(见图6),该序列最先用于储层岩石内部磁场梯度的研究[40,46,80]。

图6 改良式CPMG脉冲序列示意图[40]
改良式CPMG脉冲序列的回波幅度为
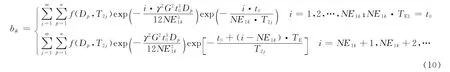
式中,bik代表第1个窗口的回波个数为NE1k时第i个回波的回波幅度;t0为第1个窗口的长度。改变第1个窗口的回波个数,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(10)联合反演,即可得到储层岩石孔隙流体的D-T2分布。
2.2.2 扩散编程脉冲序列
与改良式CPMG序列一样,扩散编程脉冲序列在时间轴上也分为2个窗口,不同的是第1个窗口内只采集2个回波,该窗口内的回波间隔从小变大,加载储层孔隙流体扩散弛豫信息;第2个窗口用仪器的最短回波间隔采集CPMG回波信号,采集储层孔隙流体横向弛豫信息、记录扩散弛豫衰减信息(见图7)。扩散编程脉冲序列的回波幅度为
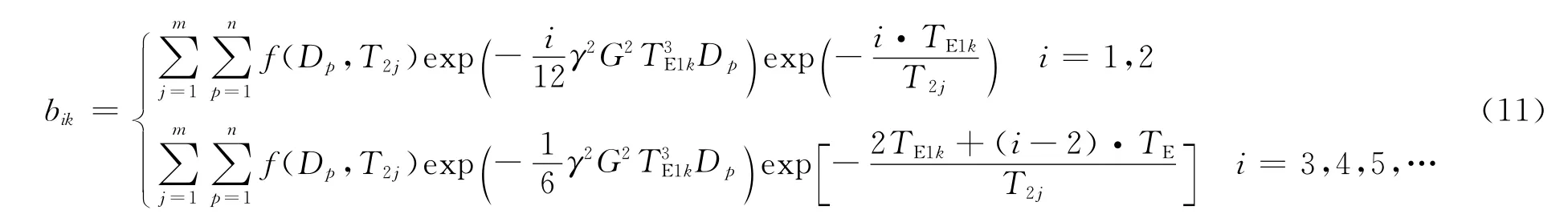
式中,bik代表第1个窗口的回波间隔为TE1k时第i个回波的回波幅度。
改变第1个窗口的回波间隔,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(11)联合反演,即可得到储层岩石孔隙流体的D-T2分布。MR Scanner的D-T2二维核磁共振测井就是采用扩散编程脉冲序列,并取得了不错的应用效果。
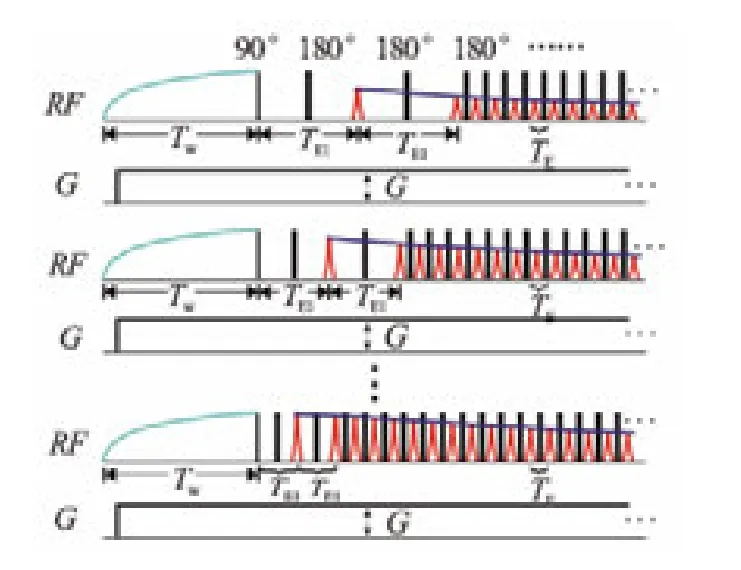
图7 扩散编程脉冲序列示意图[43]
2.2.3 多回波间隔CPMG脉冲序列
利用CPMG脉冲序列无需重新设计,只要改变回波间隔采集一系列自旋回波串即可(见图8)。
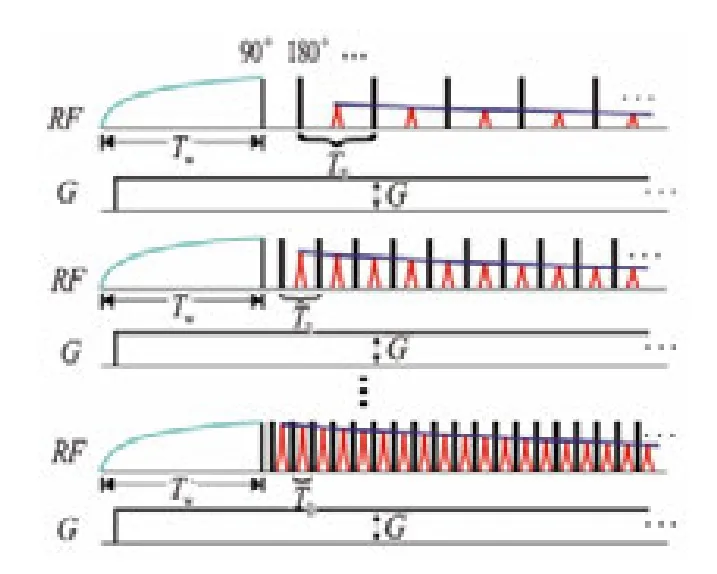
图8 多回波间隔CPMG脉冲序列示意图[39]
多回波间隔CPMG脉冲序列的回波幅度为

式中,bik代表回波间隔为TEk时第i个回波的回波幅度。改变回波间隔,采集多条CPMG回波串,实现D-T2二维数据采集,解谱时将采集的回波串簇利用式(12)联立反演[81],即可得到储层岩石孔隙流体的D-T2分布。MREX的 PP OIL、PP HEAVY OIL观测模式和MRIL新增的四TE观测模式均采用多回波间隔CPMG脉冲序列,沿用了成熟的CPMG序列,降低了D-T2核磁共振测井仪器的研发成本。
2.3 D-T2脉冲序列性能对比
上述6种常用D-T2脉冲序列的信息加载和采集示意图见图9,基本信息及性能对比见表1。总体上,得益于高磁场梯度值,脉冲梯度场D-T2脉冲序列具有较大的扩散系数测量范围,但是该类脉冲序列在梯度作用窗口内没有自旋回波信号,降低了对短弛豫组分(束缚水、稠油等)的分辨能力,此外,脉冲梯度对硬件要求更高,尤其是梯度线圈的大功率供电问题和梯度线圈的散热设计,因此能够采集DT2数据的核磁共振测井仪器都采用固定磁场梯度设计。与之相对的是,恒定梯度场梯度值一般较小,恒定梯度场D-T2脉冲序列的扩散弛豫加载能力不如前者,这也是目前核磁共振测井仪器测遇稠油层时D-T2二维谱中D轴产生拖尾现象的根源,但是该类脉冲序列在扩散弛豫加载窗口内采集自旋回波信号,或将扩散弛豫信息加载到整条CPMG回波串上,因而该类脉冲序列的横向弛豫分辨能力更胜一筹。
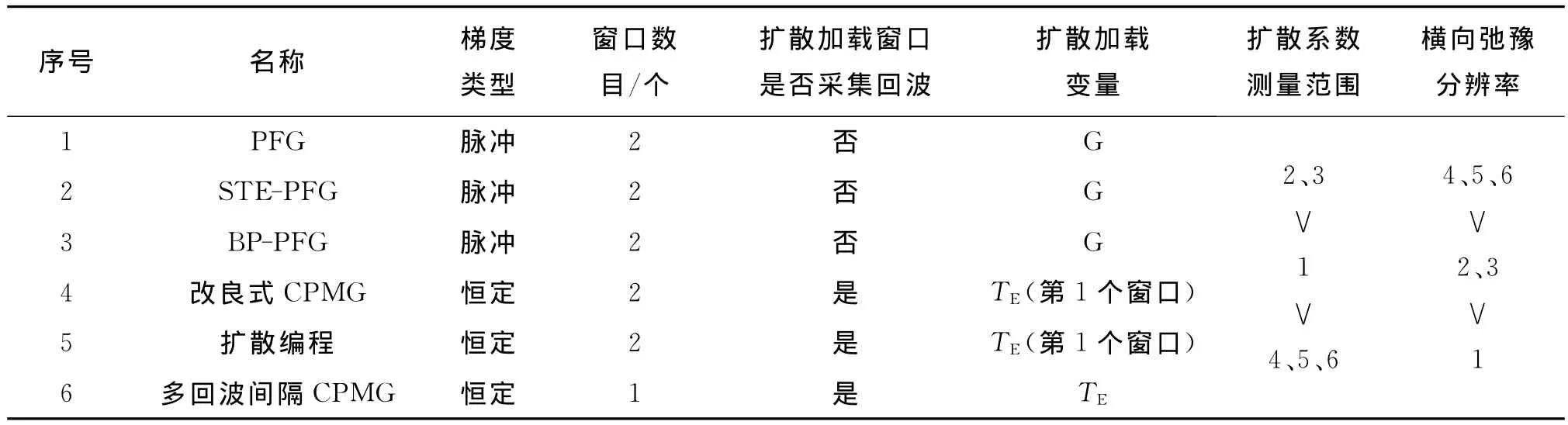
表1 6种常见D-T2脉冲序列的基本信息及性能对比
3 D-T2反演方法现状
核磁共振数据反演是典型的“反问题”求解:基于核磁共振自旋回波响应方程,代入核磁共振回波串测量数据,利用相关的数学反演方法求解目标函数的一个最优解,使拟合回波串与实测回波串的误差最小。因此,D-T2反演就是方程(4)的“反问题”求解,目标函数是氢核在(D,T2)二维空间的分布f(D,T2)。目前,D-T2核磁共振数据反演主要分为一维方法和二维方法,下面针对PFG、STE-PFG、BP-PFG、改良式CPMG、扩散编程、多回波间隔CPMG脉冲序列的数据反演问题,介绍这2种反演方法。

图9 6种常见D-T2脉冲序列信息加载和采集示意图
3.1 D-T2 二维反演方法
PFG、STE-PFG、BP-PFG脉冲序列借鉴了核磁共振波谱学中分割时间轴的设计思想,第1个窗口(梯度作用窗口)固定为t0,消除了反演系数中核函数kT和kD的耦合关系,因此方程(5)、(9)可写成矩阵形式

式中,B是D-T2实测回波串数据矩阵,大小是m×n,m是回波串条数,n是每条回波串的回波个数;KD是kD核函数组成的系数矩阵,大小是m×p,p是扩散系数D的布点个数;KT是kT核函数组成的系数矩阵,大小是q×n,q是横向弛豫时间T2的布点个数;F是目标函数f(D,T2)矩阵,大小是p×q。
李新军等[60]提出基于迭代TSVD的D-T2二维反演方法,其基本原理如下。
将KD、KT奇异值分解,得到
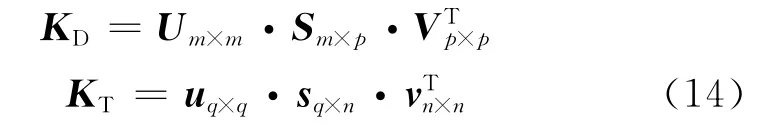
式中,U、V、u、v是正交矩阵;S、s是对角矩阵,并且对角元素从大到小排列。
将S、s的对角元素用测量数据的信噪比SNR作截断处理,得到S′、s′,则方程(13)的解可表示为

给目标函数F赋初值,结合F的非负约束条件,利用方程(15)迭代求解即可得到测量对象的DT2二维分布f(D,T2)。
3.2 D-T2 一维反演方法
改良式CPMG脉冲序列,由式(10)的回波幅度方程可知:第1个窗口的回波信号,其反演系数中kT和kD是耦合关系,无法用式(13)的矩阵表达式;第2个窗口的回波信号,其反演系数中kT和kD的耦合关系消除了,可以使用式(13)的矩阵表达式。
若2个窗口的数据同时参与反演,其矩阵表达式为

式中,b是D-T2实测回波串数据的列向量,大小是N×1,N是总回波个数;K是kD·kT组成的系数矩阵,大小是N×(p×q);f是目标函数f(D,T2)的列向量,大小是(p×q)×1。
对于方程(16)的反演处理技术已经发展成熟,主要有TSVD及其改进算法,差分进化、遗传算法等智能算法,各类正则化方法等,已经在一维核磁共振T2谱反演中得到成功应用,在D-T2数据反演中也得到拓展应用[82-93],但是这类一维反演方法在实际处理D-T2二维数据时面临提升解谱效率的困扰。扩散编程和多回波间隔CPMG脉冲序列的数据处理方法与改良式CPMG脉冲序列类似。
3.3 D-T2 反演方法对比
D-T2二维反演方法和一维反演方法的性能对比主要是解谱效率和反演精度。例如改良式CPMG序列,回波串个数10,第1个窗口的回波个数1、2、3、4、5、6、7、8、9、10,第2个窗口的回波个数1024,扩散系数反演布点数128,横向弛豫时间布点数128。
使用一维方法时,系数矩阵K的数据个数是1.6867328×108,若用单精度浮点存储,保存这个超大矩阵需要占用系统内存近0.63GB,再加上数据运算占用的缓冲内存,在单机上完成如此庞大的运算量,其时间消耗太大;借助数据压缩技术,按照特定规律选择部分回波数据参与反演,虽然可以加快运算速度,但是测量数据的人为筛选在一定程度上也降低了反演谱精度。
使用二维方法时,只使用第2个窗口的数据反演,系数矩阵KD的数据个数是1280,占用内存5kB,系数矩阵KT的数据个数是131072,占用内存0.5MB,单个反演系数矩阵的规模大大缩小,其与一维反演方法的解谱效率对比高下立判;不过二维反演方法对第1个窗口数据的人为舍弃降低了反演谱的精度,当测量对象中T2<t0的短弛豫组分含量不高时,这种数据处理方式是可行的,不过随着勘探对象的复杂化,这种数据处理方式的实用性将大打折扣。
D-T2二维反演方法解谱效率高,但第1个窗口回波数据的缺失或舍弃影响反演精度;D-T2一维方法使用所有回波数据反演,其精度虽高,但解谱效率难以与二维方法媲美。
4 结 论
(1)D-T2二维核磁共振方法作为岩石物理分析和地球物理测井的新兴技术手段,主要用于储层岩石孔隙流体识别和定量计算,弥补了一维核磁共振技术T2谱油气水重叠的短板。
(2)PFG、STE-PFG、BP-PFG等基于脉冲梯度场的D-T2脉冲序列常用于岩石物理实验分析,扩散弛豫加载变量通常是脉冲梯度输出值,其优势是扩散系数测量范围大,但短弛豫组分分辨率低。
(3)基于恒定梯度场的改良式CPMG、扩散编程、多回波间隔CPMG脉冲序列主要用于核磁共振测井仪器的二维数据采集,扩散弛豫加载变量是回波间隔,其优势是短弛豫组分分辨率高,但扩散系数测量范围偏小。
(4)目前2个窗口的D-T2二维核磁共振数据反演主要分为一维方法和二维方法:二维方法解谱效率高,但第1个窗口回波数据的缺失或舍弃降低了反演精度;一维方法使用所有回波数据反演,其精度虽高,但解谱效率难以与二维方法媲美。
(5)面对油气勘探对象日益复杂的挑战,为突破现有D-T2脉冲序列无法兼顾扩散系数测量范围和横向弛豫分辨率的技术瓶颈,解决现有D-T2反演方法无法兼顾解谱效率和反演精度的约束,设计扩散系数测量范围大、横向弛豫分辨率高的多变量新型D-T2脉冲序列,研发高效、高精度的D-T2反演方法,是D-T2二维核磁共振技术未来的发展目标和方向。
[1]Torrey H C,Korringa J,Seevers D O.Magnetic Spin Pumping in Fluids Contained in Porous Media[J].Physical Review Letters,1959,3:418-419.
[2]Brown R J S,Gamson B W.Nuclear Magnetism Logging[J].Journal of Petroleum Technology,1960,219:201-209.
[3]Timur A.Effective Porosity and Permeability of Sandstones Investigated Through Nuclear Magnetic Resonance Principles[C]∥SPWLA 9th Annual Logging Symposium,New Orleans,LA,1968,Paper K.
[4]Timur A.Pulsed Nuclear Magnetic Resonance Studies of Porosity,Moveable Fluid,and Permeability of Sandstones[J].Journal of Petroleum Technology,1969,21:775-786.
[5]Herrick R C,Couturie S H,Best D L.An Improved Nuclear Magnetism Logging System and Its Application to Formation Evaluation[C]∥SPE Annual Conference,Las Vegas,NV,1979,Paper 8361.
[6]Morriss C E,Macinnis J,Freedman R,et al.Field Test of an Experimental Pulsed Nuclear Magnetism Tool[C]∥SPWLA 34th Annual Logging Symposium,Calgary,Alberta,Canada,1993,Paper GGG.
[7]Dunn K J,LaTorraca G A,Warner J L,et al.On the Calculation and Interpretation of NMR Relaxation Time Distributions[C]∥SPE Annual Conference,New Orleans,LA,1994,Paper 28367.
[8]Chang D,Vinegar H J,Morriss C E,et al.Effective Porosity Producible Fluid and Permeability in Carbonates from NMR Logging[C]∥SPWLA 35th Annual Logging Symposium,Tulsa,Oklahoma,1994,Paper A.
[9]LaTorraca G A,Dunn K J,Bergman D J.Magnetic Susceptibility Contrast Effects on NMRT2Logging[C]∥SPWLA 36th Annual Logging Symposium,Paris,1995,June 26-29,Paper JJ.
[10]Coates G R,Marshall D,Mardon D,et al.A New Characterization of Bulk-volume Irreducible Using Magnetic Resonance[C]∥SPWLA 38th Annual Logging Symposium,Houston,Texas,1997,Paper QQ.
[11]Kleinberg R L,Boyd A.Tapered Cutoffs for Magnetic Resonance Bound Water Volume[C]∥SPE Annual Conference,San Antonio,1997,Paper 38737.
[12]Appel M,Stallmach F,Thomann H.Irreducible Fluid Saturation Determined by Pulsed Field Gradient NMR[J].Journal of Petroleum Science and Engineering,1998,19(1):45-54.
[13]李召成,孙建孟,耿生臣,等.应用核磁共振测井T2谱划分裂缝型储层[J].石油物探,2001,40(4):113-118.
[14]李召成,孙建孟,耿生臣,等.核磁共振测井T2,cutoff确定方法探讨[J].测井技术,2001,25(3):175-178.
[15]王为民,郭和坤,叶朝辉.利用核磁共振可动流体评价低渗透油田开发潜力[J].石油学报,2001,22(6):40-44.
[16]Richard S.Coates and SDR Permeability:Two Variations on the Same Theme[J].Petrophysics,2002,43(1):38-46.
[17]肖立志,刘堂晏,傅容珊,等.利用核磁共振测井评价储层的捕集能力[J].石油学报,2004,25(4):38-41.
[18]何雨丹,毛志强,肖立志,等.核磁共振T2分布评价岩石孔径分布的改进方法[J].地球物理学报,2005,48(2):373-378.
[19]范宜仁,倪自高,邓少贵,等.储层性质与核磁共振测量参数的实验研究[J].石油实验地质,2005,27(6):624-626.
[20]Liu Z H,Zhou C C,Liu G Q,et al.An Innovative Method to Evaluate Formation Pore Structure Using NMR Logging Data[C]∥SPWLA 48th Annual Logging Symposium,2007,Austen,TX,Paper S.
[21]谢然红,肖立志,傅少庆,等.原油的变温核磁共振弛豫特性实验研究[J].中国石油大学学报:自然科学版,2007,31(4):34-37.
[22]谢然红,肖立志,傅少庆.饱和水岩石核磁共振表面弛豫温度特性[J].中国石油大学学报:自然科学版,2008,32(2):44-47.
[23]蔡剑华,郭和坤,刘卫.核磁共振岩屑录井及现场应用研究[J].石油地球物理勘探,2008,43(4):453-456.
[24]杨正明,郭和坤,姜汉桥,等.火山岩气藏不同岩性核磁共振实验研究[J].石油学报,2009,30(3):400-403.
[25]王克文,李宁.储层特性与饱和度对核磁T2谱影响的数值模拟[J].石油学报,2009,30(3):422-426.
[26]肖亮,刘晓鹏,毛志强.结合NMR和毛管压力资料计算储层渗透率的方法[J].石油学报,2009,30(1):100-103.
[27]刘卫,肖忠祥,杨思玉,等.利用核磁共振(NMR)测井资料评价储层孔隙结构方法的对比研究[J].石油地球物理勘探,2009,44(6):773-778.
[28]毛志强,张冲,肖亮.一种基于核磁共振测井计算低孔低渗气层孔隙度的新方法[J].石油地球物理勘探,2010,45(1):105-109.
[29]葛新民,范宜仁,吴飞,等.岩石核磁共振T2谱与电阻率指数的对应性研究[J].中国石油大学学报:自然科学版,2012,36(6):53-56.
[30]孙建孟,赵建鹏,闰伟超,等.应用核磁T2谱与数字岩心技术计算粒度分布方法[J].中国石油大学学报:自然科学版,2013,37(3):57-62.
[31]Akkurt R,Vinegar H J,Tutunjian P N,et al.NMR Logging of Natural Gas Reservoirs[C]∥SPWLA 36th Annual Logging Symposium,Paris,1995,Paper N.
[32]Looyestijn W J.Determination of Oil Saturation from Diffusion NMR Logs[C]∥SPWLA 37th Annual Logging Symposium,New Orleans,LA,1996,Paper SS.
[33]Mardon D,Gardner J S,Coates G R,et al.Experimental Study of Diffusion and Relaxation of Oil-water Mixtures in Model Porous Media[C]∥SPWLA 37th Annual Logging Symposium,New Orleans,LA,1996,Paper K.
[34]Akkurt R,Mardon D,Gardner J S,et al.Enhanced Diffusion:Expanding the Range of NMR Direct Hydrocarbon-typing Applications[C]∥SPWLA 39th Annual Logging Symposium,Keystone,Colorado,1998,Paper GG.
[35]Akkurt R,Marshall D M,Eyvazzadeh R Y,et al.Determination of Residual Oil Saturation Using Enhanced Diffusion[C]∥SPE Annual Conference,1998,Paper 49014.
[36]谢然红,肖立志,刘家军.核磁共振测井时域分析法数值模拟及影响因素分析[J].地球物理学报,2011,54(8):2184-2192.
[37]李洋,肖立志,孙华峰.核磁共振测井TDA识别油气的影响因素[J].波谱学杂志,2012,29(1):21-31.
[38]肖立志.我国核磁共振测井应用中的若干重要问题[J].测井技术,2007,31(5):401-407.
[39]谢然红.陆相油气藏核磁共振测井应用基础与二维方法研究[D].北京:中国石油大学(北京),2008.
[40]Sun B Q,Dunn K J.Probing the Internal Field Gradients of Porous Media[J].Phys Rev E,2002,65(5):051309.
[41]Sun B Q,Dunn K J.Core Analysis with Two Dimensional NMR[C]∥International Symposium of the Society of Core Analysts,Monterey,USA,2002,Paper 38.
[42]Hürlimann M D,Venkataramanan L.Quantitative Measurement of Two Dimensional Distribution Functions of Diffusion and Relaxation in Grossly Inhomoge-neous Fields.Journal of Magnetic Resonance,2002,157(1):31-42.
[43]Hürlimann M D,Venkataramanan L,Flaum C,et al.Diffusion-editing:New NMR Measurement of Saturation and Pore Geometry[C]∥SPWLA 43rd Annual Logging Symposium,Oiso,Japan,2002,Paper FFF.
[44]Hürlimann M D,Venkataramanan L,Flaum C.The Diffusion-spin Relaxation Time Distribution Function as an Experimental Probe to Characterize Fluid Mixtures in Porous Media[J].Journal of Chemical Physics,2002,117(22):10223-10232.
[45]Song Y Q,Venkataramanan L,Hürlimann M D,et al.T1-T2Correlation Spectra Obtained Using a Fast Two-dimensional Laplace Inversion[J].Journal of Magnetic Resonance,2002,154(2):261-268.
[46]邓克俊.核磁共振测井理论及应用[M].东营:中国石油大学出版社,2010:9-148.
[47]Hürlimann M D,Flaum M,Venkataramanan L,et al.Diffusion-relaxation Distribution Functions of Sedimentary Rocks in Different Saturation States[J].Magnetic Resonance Imaging,2003,21(3):305-310.
[48]Flaum M,Chen J,Hirasaki G J,et al.NMR Diffusion Editing forD-T2Maps:Application to Recognition of Wettability Change[C]∥SPWLA 45th Annual Logging Symposium,Noordwijk,Holland,2004,Paper JJ.
[49]Sun B Q,Dunn K J,Bilodeau B J,et al.Two-dimensional NMR Logging and Field Test Results[C]∥SPWLA 45th Annual Logging Symposium,Noordwijk,Holland,2004,Paper KK.
[50]Sun B Q,Dunn K J.Two-dimensional Nuclear Magnetic Resonance Petrophysics[J].Magnetic Resonance Imaging,2005,23(2):259-262.
[51]Sun B Q,Oloson M,Baranowski J,et al.Direct Fluid Typing and Quantification of Orinoco Belt Heavy Oil Reservoirs Using 2DNMR Logs[C]∥SPWLA 47th Annual Logging Symposium,Veracruz,Mexico,2006,Paper EE.
[52]顾兆斌,刘卫.核磁共振二维谱反演[J].波谱学杂志,2007,24(3):311-319.
[53]谢然红,肖立志.(T2,D)二维核磁共振测井识别储层流体的方法[J].地球物理学报,2009,52(9):2410-2418.
[54]顾兆斌,刘卫,孙佃庆,等.2DNMR技术在石油测井中的应用[J].波谱学杂志,2009,26(4):560-568.
[55]石玉江,刘天定.二维核磁共振测井技术在长庆油田的应用[J].测井技术,2009,33(6):584-588.
[56]谭茂金,邹友龙,刘兵开,等.气水模型(T2,D)二维核磁共振测井数值模拟及参数影响分析[J].测井技术,2011,35(2):130-136.
[57]谭茂金,邹友龙.(T2,D)二维核磁共振测井混合反演方法与参数影响分析[J].地球物理学报,2012,55(2):683-692.
[58]胡法龙,周灿灿,李潮流,等.基于弛豫-扩散的二维核磁共振流体识别方法[J].石油勘探与开发,2012,39(5):552-558.
[59]郭书生,李国军,张文博,等.MRX二维核磁共振在南海西部低电阻率低渗透率气层评价中的应用[J].测井技术,2012,36(2):207-210.
[60]李新军,聂生东,王远军,等.低场核磁共振扩散-横向弛豫二维反演算法[J].波谱学杂志,2013,30(3):322-335.
[61]Tan M J,Zou Y L,Zhou C C.A New Inversion Method for(T2,D)2DNMR Logging and Fluid Typing[J].Computers & Geosciences,2013,51(2):366-380.
[62]周小龙,聂生东,王远军,等.基于迭代TSVD的NMR二维谱反演算法[J].波谱学杂志,2013,30(4):541-551.
[63]Stejskal E O,Tanner J E.Spin Diffusion Measurement:Spin Echoes in the Presence of a Time-dependent Field Gradient[J].The Journal of Chemical Physics,1965,42(1):288-292.
[64]Stejskal E O.Use of Spin Echoes in a Pulsed Magnetic-field Gradient to Study Anisotropic Restricted Diffusion and Flow[J].The Journal of Chemical Physics,1965,43(10):3597-3603.
[65]Tanner J E.Use of the Stimulated Echo in NMR Diffusion Studies[J].The Journal of Chemical Physics,1970,52(5):2523-2526.
[66]Karlicek J R F,Lowe I J.A Modified Pulsed Gradient Technique for Measuring Diffusion in the Presence of Large Background Gradient[J].Journal of Magnetic Resonance,1980,37(1):75-91.
[67]Cotts R M,Hoch M J R,Sun T,et al.Pulsed Field Gradient Stimulated Echo Methods for Improved NMR Diffusion Measurements in Heterogeneous Systems[J].Journal of Magnetic Resonance,1989,83:252-266.
[68]Latour L L,Li L,Sotak C H.Improved PFG Stimulated-Echo Method for the Measurement of Diffusion in Inhomogeneous Fields[J].Journal of Magnetic Resonance:Series B,1993,101(1):72-77.
[69]Vandusschoten D.Flexible PFG NMR Desensitized for Susceptibility Artifacts,Using the PFG Multiple-Spin-Echo Sequence[J].Journal of Magnetic Resonance:Series A,1995,112(2):237-240.
[70]Wu D,Chen A,Johnson J C S.An Improved Diffusion Ordered Spectroscopy Experiment Incorporating Bipolar-gradient Pulses[J].Journal of Magnetic Resonance:Series A,1995,115(2):260-264.
[71]Snaar J E M,Hills B P.Constant Gradient Stimulated Echo Studies of Diffusion in Porous Materials at High Spectrometer Fields[J].Magnetic Resonance Imaging,1997,15(8):983-992.
[72]Mair R W,Cory G D,Peled S.Pulsed Field Gradient Measurements of Time-dependent Gas Diffusion[J].Journal of Magnetic Resonance,1998,135(2):478-486.
[73]William S P.Pulsed-field Gradient Nuclear Magnetic Resonance as a Tool for Studying Translational Diffusion:Part II Experimental Aspects[J].Concepts in Magnetic Resonance,1998,10(4):197-237.
[74]Zhang X,Li C H,Ye C H,et al.Determination of Molecular Self-diffusion Coefficient Using Multiple Spin-echo NMR Spectroscopy with Removal of Convection and Background Gradient Artifacts[J].Anal Chem,2001,73:3528-3534.
[75]龚国波,孙伯勤,刘买利,等.岩心孔隙介质中流体的核磁共振弛豫[J].波谱学杂志,2006,23(3):379-395.
[76]Albina R.M,Vladimir D S.Porous Media Characterization by PFG and IMFG NMR[J].Journal of Magnetic Resonance,2007,188(1):122-128.
[77]Zheng G,William S P.MAG-PGSTE:A New STE-based PGSE NMR Sequence for the Determination of Diffusion in Magnetically Inhomogeneous Samples[J].Journal of Magnetic Resonance,2008,195(1):40-44.
[78]Hunter M W,Jackson A N,Callaghan P T.PGSE NMR Measurement of the Non-local Dispersion Tensor for Flow in Porous Media[J].Journal of Magnetic Resonance,2010,204(1):11-20.
[79]曲岩涛,姜志敏,史京生,等.水驱油过程的核磁共振二维谱研究[J].波谱学杂志,2012,29(1):51-59.
[80]吴飞,范宜仁,邓少贵,等.储层岩石T2-G实验采集参数自动匹配技术研究[J].中国石油大学学报:自然科学版,2014,38(4):50-56.
[81]谢然红,肖立志,刘家军,等.核磁共振多回波串联合反演方法[J].地球物理学报,2009,52(11):2913-2919.
[82]王为民,李培,叶朝辉.核磁共振弛豫信号的多指数反演[J].中国科学:A辑,2001,31(8):730-736.
[83]Venkataramanan L,Song Y Q,Hürlimann M D.Solving Fredholm Integrals of the First Kind with Tensor Product Structure in 2and 2.5Dimensions[C]∥IEEE Transactions on Signal Processing,2002,50(5):1017-1026.
[84]王忠东,肖立志,刘堂宴.核磁共振弛豫信号多指数反演新方法及其应用[J].中国科学:G辑,2003,33(4):323-332.
[85]姜瑞忠,姚彦平,苗盛,等.核磁共振T2谱奇异值分解反演改进算法[J].石油学报,2005,26(6):57-59.
[86]Sun B Q,Dunn K J.A Global Inversion Method of Multi-dimensional NMR Logging[J].Journal of Magnetic Resonance,2005,172(1):152-160.
[87]Tonning E,Polders D,Callaghan P T,et al.A Novel Improved Method for Analysis of 2DDiffusion-relaxation Data-2DPARAFAC-Laplace Decomposition[J].Journal of Magnetic Resonance,2007,188(1):10-23.
[88]潘克家,陈华,谭永基.基于差分进化算法的核磁共振T2谱多指数反演[J].物理学报,2008,57(9):5956-5961.
[89]马建海,孙建孟,孙萌,等.基于迭代Tikhonov正则化的核磁测井解谱方法研究[J].西南石油大学学报:自然科学版,2009,31(1):37-40.
[90]Lin F,Wang Z W,Li J Y,et al.Study on Algorithms of Low SNR Inversion ofT2Spectrum in NMR[J].Applied Geophysics,2011,8(3):233-238.
[91]Ito K,Jin B T.A New Approach to Nonlinear Constrained Tikhonov Regularization[J].Inverse Problems,2011,27(10):5005-5027.
[92]Iain J D.On the Inversion of Diffusion NMR Data:Tikhonov Regularization and Optimal Choice of the Regularization Parameter[J].Journal of Magnetic Resonance,2011,211(2):178-185.
[93]高阳,肖立志,谢庆明.基于BG理论确定Phillips方法的正则化参数并评价反演结果[J].中国石油大学学报:自然科学版,2014,38(3):50-56.
