Advances in Research on Atmospheric Energy Propagation and the Interactions between Different Latitudes
2015-12-12YANGSongDENGKaiqiang邓开强TINGMingfang丁敏芳andHUChundi胡春迪
YANG Song(杨 崧), DENG Kaiqiang*(邓开强), TING Mingfang(丁敏芳), and HU Chundi(胡春迪)
1 Department of Atmospheric Sciences,Sun Yat-Sen University,Guangzhou 510275,China
2 Institute of Earth Climate and Environment System,Sun Yat-Sen University,Guangzhou 510275,China
3 Lamont-Doherty Earth Observatory,Columbia University,Palisades,NY 10964,USA
4 School of Atmospheric Sciences,Nanjing University,Nanjing 210023,China
Advances in Research on Atmospheric Energy Propagation and the Interactions between Different Latitudes
YANG Song1,2(杨 崧), DENG Kaiqiang1,2*(邓开强), TING Mingfang3(丁敏芳), and HU Chundi4(胡春迪)
1 Department of Atmospheric Sciences,Sun Yat-Sen University,Guangzhou 510275,China
2 Institute of Earth Climate and Environment System,Sun Yat-Sen University,Guangzhou 510275,China
3 Lamont-Doherty Earth Observatory,Columbia University,Palisades,NY 10964,USA
4 School of Atmospheric Sciences,Nanjing University,Nanjing 210023,China
Early theoretical analyses indicated that the tropics and extratropics are relatively independent due to the existence of critical latitudes.However,considerable observational evidence has shown that a clear dynamical link exists between the tropics and midlatitudes.To better understand such atmospheric teleconnection, several theories of wave energy propagation are reviewed in this paper:(1)great circle theory,which reveals the characteristics of Rossby waves propagating in the spherical atmosphere;(2)westerly duct theory,which suggests a“corridor”through which the midlatitude disturbances in one hemisphere can propagate into the other hemisphere;(3)energy accumulation-wave emanation theory,which proposes processes through which tropical disturbances can affect the atmospheric motion in higher latitudes;(4)equatorial wave expansion theory,which further explains the physical mechanisms involved in the interaction between the tropics and extratropics;and(5)meridional basic flow theory,which argues that stationary waves can propagate across the tropical easterlies under certain conditions.In addition,the progress made in diagnosing wave-flow interaction,particularly for Rossby waves,inertial-gravity waves,and Kelvin waves,is also reviewed.The meridional propagation of atmospheric energy exhibits significant annual and interannual variations,closely related to ENSO and variation in the westerly jets and tropical upper-tropospheric troughs,amongst others.
great circle path,westerly duct,energy accumulation,lateral wave expansion,meridional basic flow
1.Introduction
The classic pattern of the meridional structure of global atmospheric circulation can be attributed to the combined effect of the uneven distribution of solar radiation,earth's rotation,and mass continuity. Westerly winds prevail in the mid-high latitudes,sandwiched by easterly trade winds in the low latitudes and easterlies in the polar latitudes.The uneven distribution of land and ocean,and the complex topography of earth's surface result in complicated and zonally asymmetric patterns of atmospheric general circulation,responsible for the distinct weather and climate in different parts of the world.Earth's atmosphere can be regarded as an integrated and continuous fluid,and disturbances in one specific region will certainly affect the atmospheric motion in other regions.For example,strong convective disturbance is almost perennial in the tropics.But to what extent do these tropical disturbances affect the midlatitudes?Similarly,how does frontal activity in the midlatitudes influence atmospheric motion in the tropics,and even that in the
other hemisphere? If links exist between the atmospheric motion in different regions,do they follow the same general rules?These questions form the focus of this review article.In addition,understanding the links and physical mechanisms of atmospheric activity in different regions will undoubtedly improve the accuracy of weather and climate prediction(Ding,2009).
Since the invention of radiosonde in 1928,the quantity and availability of upper atmospheric observations has grown markedly.A specific wave pattern with a scale of several thousands of kilometers was found in the mid-upper troposphere over the midlatitude regions.Rossby(1939)first pointed out that the formation of this type of wave is due to earth's rotation and the variation in the Coriolis effect with latitude(β effect).This type of wave is thereby known as the Rossby wave.Based on the differences on spatial and temporal scales,Rossby waves can be divided into synoptic-and planetary-scale Rossby waves (Tan,2008).Jaw(1946),Charney(1947),and Eady (1949)investigated synoptic-scale Rossby waves and argued that their genesis and development are due to atmospheric baroclinity. Charney and Eliassen (1949),Bolin(1950),and Smagorinsky(1953)studied planetary-scale Rossby waves and found that topographic forcing and diabatic heating are the triggers for stationary planetary waves.Yeh(1949)made a significant contribution to the theory of Rossby wave propagation in a pioneering study of Rossby wave energy dispersion and the upstream-downstream effects of one-dimensional Rossby wave propagation. The theory of energy dispersion has important implications for how the atmospheric disturbance in a specific region can affect the activity in other remote regions, via wave propagation and energy dispersion.
By the mid 1960s,studies of midlatitude atmospheric wave dynamics had already reached a mature stage.However,studies of tropical atmospheric wave dynamics had only just begun,due partly to the lack of observations over the tropical oceans at that time.Matsuno(1966)obtained an analytical solution of tropical waves based on shallow-water equations.Soon after,based on the observational analysis,Yanai and Maruyama(1966),Maruyama and Yanai(1967),and Wallace and Kousky(1968)verified the existence of mixed Rossby-gravity and Kelvin waves. Since then,rapid advancements have been made in tropical wave dynamics.The majority of research carried out indicates that tropical atmospheric waves play a crucial role in the development of convection,in troposphere-stratosphere interaction,and in the ENSO cycle(Lindzen and Holton,1968;Holton and Lindzen,1972;Hirota,1978;Jin,1997a,b;Baldwin et al.,2001).
Alongside the above progress,research has also focused on the interaction between the tropics and extratropics.Based on scale analysis,Charney(1963) explored the large-scale atmospheric motion in the tropics,arguing that perturbation energy in the tropical upper troposphere largely comes from the eddy activity within subtropical westerly jets,while perturbations in the tropical lower troposphere mainly arise from the unstable basic flow itself or from convective heating in the intertropical convergence zone(ITCZ). In a study of large-scale circulation over the tropical Pacific,Yanai et al.(1968)found two separate frequency spectral peaks in the troposphere–one located close to the sea surface,and the other at the top of the troposphere,consistent with Charney(1963).Mak (1969)also pointed out that the mechanism for the generation of disturbances in the tropical upper troposphere is a response of the stable barotropic tropics to the unstable baroclinic temperate zone.Charney (1969)further indicated that meridional propagation of both synoptic-and planetary-scale waves can occur only when the zonal phase speed of Rossby waves is less than the speed of mean zonal flow. When a synoptic-scale midlatitude perturbation propagates equatorward and reaches a specific latitude where the zonal phase speed of perturbation is equal to the speed of mean zonal flow,it will stop propagating toward the equator.This latitude is the so-called critical latitude/layer.Numerous studies have investigated the interaction between waves and mean flow within the critical layer.For example,Dickinson(1968,1970), Bennett and Young(1971),and Geisler and Dickinson (1975)explored the linear interaction between Rossby waves and the critical layer;B´eland(1976)and Warn
and Warn(1978)studied the nonlinear interaction between Rossby waves and the critical layer;Killworth and McIntyre(1985)and Brunet and Haynes(1996) suggested that Rossby waves can be absorbed,reflected or even super-reflected at critical latitudes.
In other words,the critical latitude acts like a“barrier”that blocks the interaction between the tropics and extratropics.However,there is much observational evidence of significant links between the atmospheric motion of the tropics and extratropics,and even between the Northern Hemisphere(NH)and the Southern Hemisphere(SH).Radok and Grant(1957) argued that westerlies sometimes appear in the upper troposphere over Australia during boreal winter, associated with synoptic activity north of the equator.Based on observational data from tropical stations,Tucker(1965)found large meridional variation in time-averaged zonal winds.Weak westerlies occur in the upper troposphere in the Western Hemisphere and are accompanied by strong cross-equatorial momentum flux,while the Eastern Hemisphere is under the control of strong easterlies.Based on balloon observations in the SH upper troposphere,Webster and Curtin(1975)found a large-scale slow-moving trough in the midlatitudes,which tilts in a southeastnorthwest direction horizontally,and is quite distinct over the Pacific.This feature indicates that there is a large amount of momentum flux transported from the tropics to the midlatitudes.Murakami and Unninayar(1977)used U.S.National Meteorological Center observational data to compare the time-mean distribution of zonal winds and turbulent kinetic energy, and found the location of perturbation kinetic energy in the equatorial area to be highly correlated with the zonal winds.
The need to better understand observational results led to the development of many theoretical models that explore the physical mechanisms underpinning the interaction of atmospheric motion in different latitudes.In this review,we focus on great circle theory, westerly duct theory,energy accumulation and wave emanation theory,equatorial wave lateral expansion theory,and meridional basic flow theory,in explaining the atmospheric interaction between different latitudes,especially that between the mid and low latitudes,and between the NH and SH.In addition,we also briefly discuss the advancements that have been made in the use of wave activity flux,a powerful tool for diagnostic analysis of wave energy propagation and wave-mean flow interaction.
2.Great circle theory
Based on one-point correlation analyses,Horel and Wallace(1981)and Wallace and Gutzler(1981) found a significant teleconnection pattern in the NH winter at the 500-hPa geopotential height.Due to the importance of atmospheric teleconnection for weather and climate prediction,scientists have since been attempting to understand the nature of atmospheric teleconnections.The two-dimensional wave propagation theory proposed by Hoskins et al.(1977)and Hoskins and Karoly(1981)is a representative work of such studies.
Atmospheric energy dispersion emerged as a theory following the early work of Yeh(1949). However,Yeh's formula is limited to one-dimensional wave propagation,when the real atmosphere is on a two-dimensional sphere.To understand planetary wave propagation on a spherical surface,Hoskins et al.(1977)investigated the propagation characteristics of perturbation vorticity using the linear barotropic vorticity equation.Grose and Hoskins(1979)subsequently studied the propagation of linear Rossby waves triggered by large-scale topography in the zonal mean basic flows.They found that a topographyforced Rossby wave tends to split into northward-and southward-propagating wave trains downstream of the topography.The northward-propagating wave train north of 40°N possesses a longer wavelength than the southward-propagating one when using the 300-hPa boreal winter zonal mean zonal flow as the basic state. Note,however,that Grose and Hoskins(1979)only investigated barotropic wave propagation in their study. Considering the strong atmospheric baroclinicity in midlatitude winter,Hoskins and Karoly(1981)used a five-layer baroclinic model to further investigate the atmospheric responses to thermal forcing and large-
scale topography.
Sea surface temperature(SST)anomalies can often lead to vertical motion(Bjerknes,1966). Gill (1980)studied the tropical atmospheric response to diabatic heating by using a simple theoretical model. It indicated that eastward-propagating Kelvin waves and westward-propagating Rossby waves are triggered if there is a localized heat source symmetrical with respect to the equator.Hence,it is important to study the remote atmospheric responses to,and the propagation of disturbance triggered by local heating.
Hoskins and Karoly(1981)imposed a negative vortex anomaly in the upper troposphere to represent atmospheric thermal forcing.As shown in Fig. 1,they found that the perturbation vorticity initially propagated northeastward,and then the wave later started to split.The relatively longer of the resultant two waves continued to propagate poleward and even crossed the north pole to the other hemisphere.Meanwhile,the shorter wave turned to propagate equatorward.A large number of experiments(Hoskins and Karoly,1981)indicated that the basic propagation pattern of the perturbation vorticity is insensitive to the location and intensity of the thermal forcing,although the phase and amplitude of the wave may be affected.That is to say,the wave train will only propagate northward,eastward,or equatorward,consistent with results derived from barotropic models.
In addition to thermal forcing,the effect of largescale topography cannot be ignored.Due to the β effect,extra-long Rossby waves can generate cyclones over mountain ridges.In contrast,for other relatively short-length waves,anticyclones are produced over mountains due to zonal vorticity advection.Hence, topographic forcing exerts different effects on waves of different wave lengths,and thus the phases of teleconnections may be different(Smith,1979).Therefore, large-scale topography is another source for triggering atmospheric disturbance.
Hoskins and Karoly(1981)proposed that vorticity and geopotential height disturbances would appear at 300 hPa if large-scale topography was inserted into the westerlies. The propagation of the wave train would split around 40°N,with the relatively long waves propagating poleward while short waves move equatorward,again consistent with results from barotropic models.
Numerical modeling indicates that large-scale Rossby waves propagating in a slowly varying medium are quasi-barotropic. Using the non-divergent linear barotropic vorticity equation,Hoskins and Karoly (1981)obtained the Rossby wave dispersion relation on a two-dimensional spherical surface as follows:


Fig.1.Steady state,linear solutions of a five-layer baroclinic model for a deep elliptical heat source at 15°N perturbing the NH winter zonal flow.(a)300-hPa vorticity perturbation(contour interval:0.05 Ω)and(b)300-hPa height field perturbation(contour interval:2 dam).Hatching in(b)is the region of heating greater than 0.5 K day−1.[Source: Hoskins and Karoly(1981)].
where ω is frequency,k and l are zonal and meridional
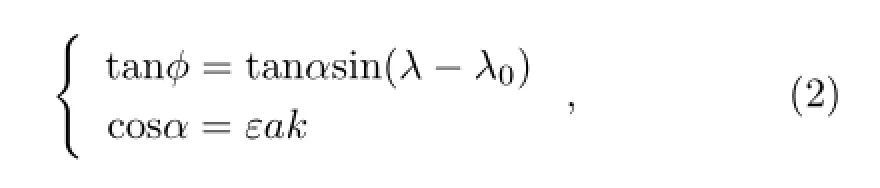
where α is the so-called turning latitude,where the meridional propagation of the Rossby wave will reverse its direction;λ0is the longitude where the initial perturbation is located;and ε2=¯ω[2(Ω+¯ω)]−1.According to the ray theory for wave propagation,this equation actually yields a great circle path(Longuet-Higgins,1964).Along this circular path,Rossby wave energy propagates at a speed of Cg= 2εak(a˜ω). Therefore,once the location of the initial perturbation is decided,the propagation paths for various wavelength Rossby waves can be calculated.
Figure 2 shows the relationship between the Rossby wave propagation path,zonal wave number, and the location of the initial perturbation.Figure 2a indicates that the maximum wave amplitude occurs at higher latitudes with smaller zonal wave numbers.Figures 2b–d show that the Rossby wave propagation path is almost the same when the initial perturbation is located at 15°,25°,or 35°N.The Rossby wave splits at a specific latitude during its propagation,with the longer of the two resultant waves propagating poleward,and the shorter wave moving equatorward,forming great circle paths.
The great circle theory of Rossby wave propagation in a spherical atmosphere has been widely applied. Numerous observational and numerical studies have proven the existence of the great circle path.Many studies have shown that the midlatitude zonal westerly jet plays a waveguide role in Rossby wave propagation(Simmons and Hoskins,1979;Hoskins and Ambrizzi,1993;Ambrizzi et al.,1995).The wave train propagates along the jet axis,and strong disturbance occurs at the jet stream exit.The westerly jet wave guides are highly correlated with the East Asian“Silk Road”teleconnection pattern and NH teleconnection pattern(Enomotol et al.,2003;Ding and Wang,2005; Liu et al.,2014).Zhou et al.(2012)found that a Pacific-North America-like wave train appears in East Pacific in the NH winter,which propagates eastward and upward,and reaches the stratosphere over North America.Zheng et al.(2013)argued that wintertime precipitation anomalies over the Indian-western Pacific Ocean significantly affect atmospheric circulation in Asia.Tan et al.(2015)further pointed out that the dipole pattern of heating in the tropical western Pacific can trigger a Rossby wave train,which propagates toward the midlatitude region of the northern Pacific along the extratropical jet before turning toward East Asia and then Alaska Bay,where it finally forms the teleconnection wave train through wavemean flow interaction over the eastern Pacific.In addition,blocking and large-scale ridges and troughs also affect the great circle path of Rossby wave propagation(Trenberth,1986;Maga˜na and Yanai,1991;Suo et al.,2008).Rossby wave propagation is of great importance in modulating regional climate(Ding et al., 2014;Trenberth et al.,2014).As suggested by Chen et al.(2005),Wang et al.(2009),and Tan and Chen (2014),stationary wave activity in the NH affects the winter monsoon in Asia,and subsequently,temperature anomalies in East Asia.
Researchers in China have contributed greatly to our understanding of Rossby wave propagation, through both theoretical and numerical studies.Chao (1977)analyzed the development and dynamical features of spiral-shaped Rossby waves and their effects in maintaining atmospheric circulation.Lu and Zeng(1981)explored the evolutionary characteristics of long waves in the barotropic atmosphere,suggesting that perturbation development depends entirely on the structure of the perturbation itself,particularly the direction of the perturbation axis and its position relative to the basic flow.Zeng(1983a,b) used Wenzel-Kramers-Brillouin theory to investigate the evolutionary features of Rossby wave packets in a three-dimensional baroclinic atmosphere and suggested that the development of a wave packet is related to the nature of the wave packet itself and its
location relative to the basic flow. Through studying the vertical propagation of Rossby waves,Huang (1983)found that two wave guides exist in the wintertime NH.Liu and Tan(1988a,b)investigated the impact of topographic forcing and the β effect on Rossby wave propagation,suggesting that east-west oriented topography is conducive to the formation of troughs and shear lines,while north-south oriented topography mainly leads to shorter wavelengths for the leading waves and longer wavelengths for the dragging waves.Tan(1990,1993)also studied the stability of Rossby waves and the interactions between nonlinear Rossby waves,and suggested that the stability of Rossby waves is not only related to the spatial distribution of basic flow,but also to the structure of the wave itself and its location within the basic flow.
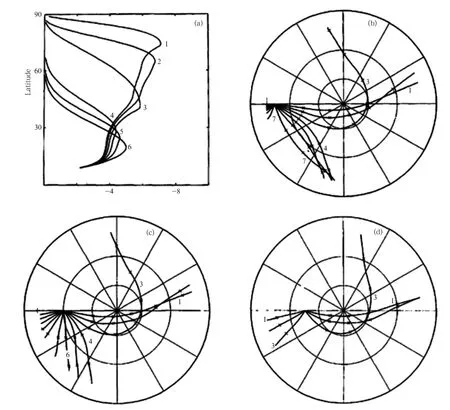
Fig.2.Northern Hemisphere 300-hPa zonal flow.(a)Amplitudes of the extrema on the rays for different zonal wave numbers;(b)a source at 15°N,with rays and phases marked by crosses every 180°;(c,d)as in(b),but for sources at 30°and 45°N,respectively.The straight and circle lines in(b),(c),and(d)indicate the longitudes and latitudes.The horizontal straight line(left-right)shows the longitudes of 0°and 180°,while the vertical line(upper-lower)shows the longitudes of 90°E and 90°W.Longitude interval is 30°along the anticlockwise direction.The circle lines indicate the latitudes of equator,30°,60°,and 90°N,respectively.[Source:Hoskins and Karoly(1981)].
3.Westerly duct theory
When studying the atmospheric interaction between different latitudes,large discrepancies exist between the theoretical critical latitude and observations
Thus,what are the possible mechanisms involved in breaking this critical latitude,allowing the propagation of midlatitude disturbance to lower latitudes and even into the other hemisphere?
Charney(1969)suggested that planetary Rossby waves can only propagate to low-latitude regions when their westward phase speed is greater than the maximum speed of tropical easterly wind.This is known as the weak westerly waveguide.However,this type of wave only contains limited energy and thus cannot exert any great impact on the atmospheric activity at low latitudes.Synoptic-scale Rossby waves cannot continue to propagate equatorward once they reach the critical latitude,since the zonal wind speed is low. Charney(1969)also indicated that the propagation of wave disturbance from the midlatitudes to the tropics often occurs in the upper troposphere and lower stratosphere,since weak easterly and westerly winds at this level are conducive to the meridional propagation of waves.
Note,however,that Charney(1969)only considered the zonally averaged basic state,which is simply a function of latitude and height.In reality,time-mean zonal flow varies with longitude as well.On the basis of Charney's argument,Webster(1973)studied the response of zonally homogeneous basic flow to a stable forcing and found that the response in the equatorial region is a slowly varying Kelvin wave,while in the midlatitude region a Rossby wave is triggered. These waves of different type are separated by a critical latitude.Later,Webster and Curtin(1975)further studied the meridional propagation of midlatitude disturbances and indicated that they dominate subtropical atmospheric perturbations;while in the tropics, changes are mainly under the influence of local effects. However,despite expanding the y−z plane to a twodimensional spherical atmosphere,the basic state considered by Webster and Curtin(1975)was still a simple pattern,with easterlies in the low latitudes and westerlies in the midlatitudes.
Murakami and Unninayar(1977)found that in the NH winter strong zonal westerly winds exist over the central and eastern tropical Pacific and Atlantic. Figure 3 shows the distribution of average perturbation kinetic energy(PKE)and zonal mean winds.As can be seen,the PKE distribution corresponds well to the distribution of zonal winds,with maximum PKE occurring within the zonal westerly wind belt in the upper troposphere.In contrast,minimum PKE occurs in the region of the tropical easterly wind belt.Webster and Holton(1982)named the mean zonal westerly in the upper troposphere above the tropical central and eastern Pacific and Atlantic,the“westerly duct”for wave energy propagation,and established the westerly duct theory for the cross-equatorial propagation of midlatitude disturbance.
Webster and Holton(1982)further considered four different types of zonal flow basic state in their shallow-water model,as shown in Fig.4.The zonal flow basic state in Fig.4 ranges from weak easterly winds across all latitudes between 15°N and 15°S(Fig. 4a),to medium strength easterly winds with a patch of weak westerly winds in the deep tropics(Fig.4b),to a similar pattern as that in Fig.4b but with both the easterly and westerly winds strengthened(Fig.4c), and finally to a similar pattern as that in Fig.4c but with a wider westerly wind duct in the deep tropics(Fig.4d).The basic state shown in Fig.4a is the same as that described by Charney(1963,1969),while that in Figs.4b and 4c resembles the real atmosphere,
as shown in Fig.3.In the equatorial area,zonally averaged winds are usually easterly.Hence,the tropical zonal mean zonal winds in Figs.4a–c are indeed easterly([u(0)]<0).To compare with the situation when zonal mean zonal winds are westerly([u(0)]>0),the westerly wind duct has been increased in Fig. 4d.
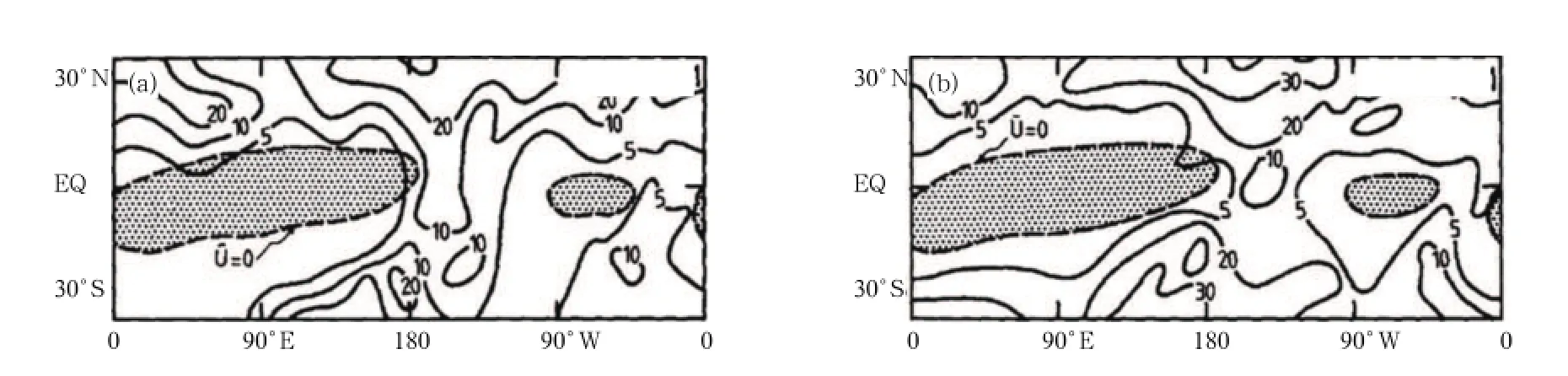
Fig.3.300-hPa perturbation kinetic energy distributions(m2s−2)for(a)January and(b)February 1971.The stippled areas enclosed by the heavy dashed lines denote the regions of mean easterly winds.[Source:Webster and Holton(1982)].
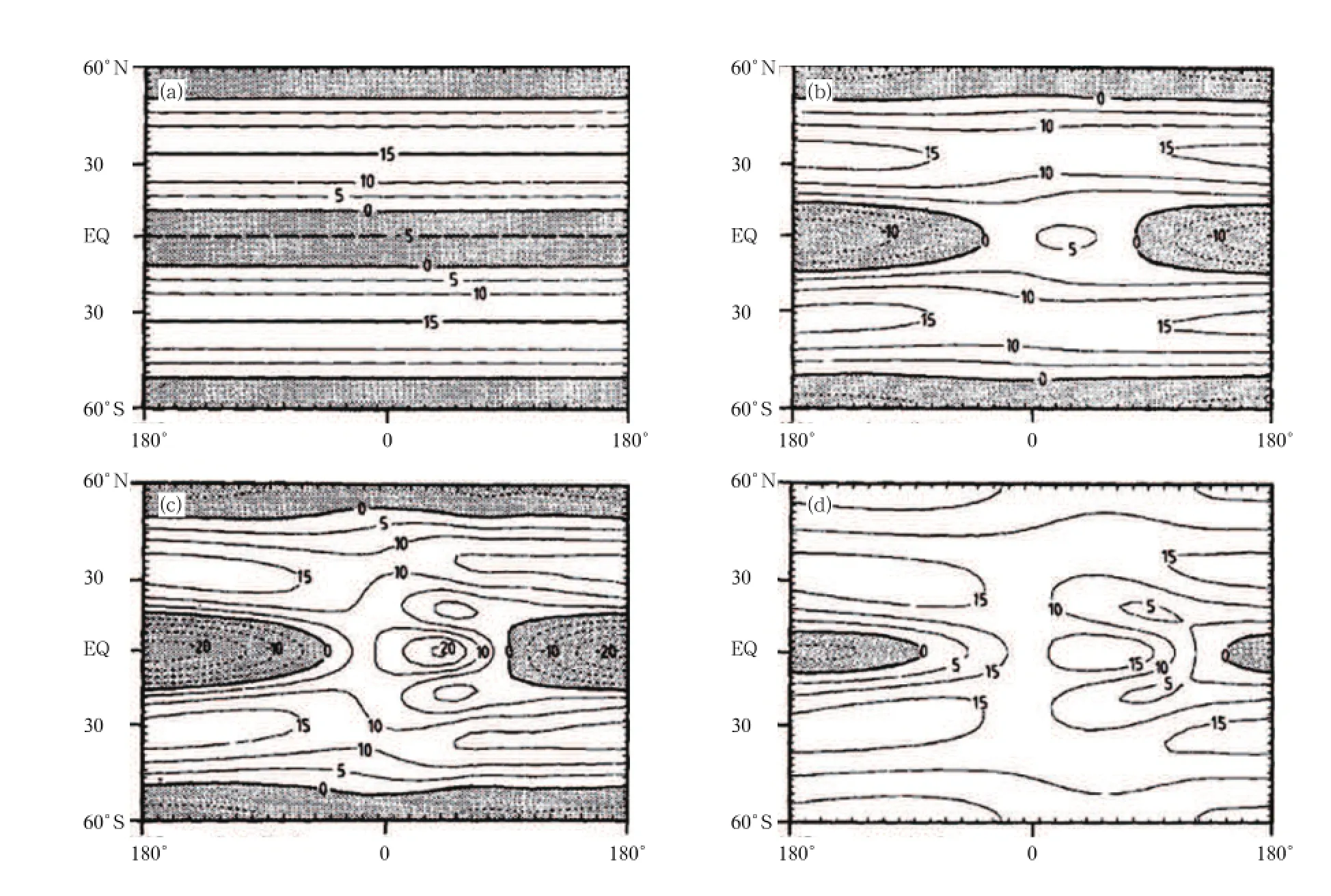
Fig.4.Distributions of the model-generated basic-state zonal wind field(m s−1)for(a)weak easterly,(b)weak westerly, and(c,d)strong westerly.The stippled areas denote the easterly wind regime.[Source:Webster and Holton(1982)].
Webster and Holton(1982)indicated that when the basic flow is in the form of weak easterly winds (Fig.4a),the wave propagation is largely restricted to the latitudes north of zonal zero wind in the NH, no matter where the initial midlatitude disturbance originated.At the location of the initial disturbance, the equatorward propagation weakens rapidly after it enters the easterly wind zone.This is because only wavenumber-1 Rossby waves can cross the weak easterly zone,which contain small amounts of energy and attenuate quickly(Charney,1963).When the basic state is in the form of weak westerly winds,as shown in Fig. 4b,the location of the initial disturbance relative to the westerly duct and its zonal scale becomes important.On the one hand,perturbations can only propagate through the westerly duct to reach the other hemisphere;on the other hand,only those disturbances with a zonal wavelength less than the zonal extension of the westerly duct can propagate across the westerly duct.The shorter the wavelength,the higher the propagation efficiency.The results from experiments with different basic states(Figs.4c and 4d)further indicate that the cross-equatorial propagation of midlatitude disturbance is closely related to the intensity and zonal extent of the westerly duct.In general,a stronger westerly duct(i.e.,greater wind speed) and larger zonal extension are more conducive to crossequatorial propagation of disturbance,which results in stronger atmospheric interaction between the two hemispheres.
Webster and Holton(1982)explained the impact of the westerly duct intensity on the propagation of the disturbance wave train theoretically.The wave dispersion relation for linear and barotropic Rossby waves can be expressed as(Holton,1979)

For a stationary wave,the phase speed is zero;thus, Eq.(3)can be written as

According to the dispersion relation,group velocity can be written as

Using Eq.(4)in Eqs.(5)and(6)yields
Equation(8)shows clearly that meridional energy propagation is only possible when the zonal mean basic state is westerly,and disturbances in strong westerly winds can propagate equatorward and reach the other hemisphere rapidly.Westerly duct theory is essentially an extension of critical latitude theory,which reveals the laws governing how midlatitude perturbations in one hemisphere affect the atmospheric behavior in the other hemisphere.The perturbation wave train originated in midlatitudes usually propagates along a great circle path,and is then absorbed or reflected when it reaches the critical latitude.However,if the perturbation wave train reaches the area where the westerly duct is located,it will continue to propagate equatorward,and even reach the other hemisphere.The meridional propagation speed of the perturbation wave train depends on the intensity and zonal extension of the westerly duct.
Westerly duct theory suggests that the atmospheric activity in the SH should be considered when predicting the weather and climate of the NH.The accurate prediction of the intensity and location of the westerly duct could help in predicting the meridional propagation of perturbation energy.The westerly duct demonstrates distinct monthly,seasonal,and interannual variations.It is strongest in winter and spring in the NH,weakening and diminishing in the summer and autumn.The interannual variation of the westerly duct is mainly related to ENSO activity.During El Ni˜no years,the westerly duct often weakens and disappears in the upper troposphere of the central and eastern Pacific and is sometimes replaced by mean easterly winds.In contrast,westerly winds intensify significantly in the upper troposphere over the Atlantic during El Ni˜no(Arkin,1982;Arkin and Webster,1985;Tomas and Webster,1994;Webster and Chang,1998).During the NH summer,the low latitudes are often under the control of tropical easterlies. However,in some years,troughs over the central North Pacific and North Atlantic may intrude into the low latitudes,leading to strong westerly winds.As a result,midlatitude disturbances in the NH summer may propagate across the equator via this route(Maga˜nna and Yanai,1991;Knippertz,2007).
4.Energy accumulation-wave emanation theory
In their study of the meridional propagation of midlatitude disturbances,Arkin and Webster(1985) and Webster and Yang(1989)found that the mean perturbation kinetic energy(PKE)in the midlatitudes is rather uniformly distributed in the vertical direction,in contrast to that in the tropics where the PKE centers and convective activity in upper and lower troposphere are out of phase.A large PKE center in the tropical upper troposphere corresponds to weak convective activity in the lower troposphere,while strong convective activity in the lower levels corresponds to a small PKE center and strong easterly wind in the upper levels.Therefore,Arkin et al.(1985)argued that large PKE values in the tropical upper troposphere are not caused by local convection.Rather,they are a consequence of the meridional propagation of midlatitude transient wave disturbance.
Webster and Chang(1988)further pointed out that a large PKE in the tropical upper troposphere derives from the meridional propagation of midlatitude disturbances,as well as nonlocal convective activity.They hypothesized that equatorial waves are triggered by tropical convection.During their zonal propagation,these equatorial waves transport PKE to zonal westerly wind belts in the upper troposphere, where PKE accumulates and results in a large PKE value.
Webster and Chang(1988)argued that the following three conditions must be satisfied for accumulating
kinetic energy in average westerly wind belt:
(1)Physical processes that can produce transient kinetic energy in the tropics;
(2)Physical mechanisms that are able to transport transient kinetic energy from its origin to where PKE accumulates;
(3)A physical mechanism responsible for the accumulation of PKE in the equatorial westerly wind zone.
Usually,points(1)and(2)are easily satisfied. Convective activity often occurs in the tropics,such as that in the Asian-Australian monsoon region and within the ITCZ.Well-organized regional convection can trigger equatorial waves,which then transport PKE from their source region to other regions through zonal propagation.In terms of point(3),Webster and Chang(1988)indicated that the zonally varying basic flow in the tropics could be responsible for PKE accumulation.
Generally,the distribution of basic flow in the real atmosphere varies zonally,and the meridional gradient of the zonal flow(¯uy)and the zonal gradient of the meridional flow(¯vx)are often referred to as basic flow shear.Here,to distinguish from the concept of conventional shear,we refer to the zonal gradient of the zonal flow(¯ux)as stretching deformation,which describes the elongation of the zonal basic flow in the east-west direction.Assuming that the zonal basic flow changes slowly with time,Webster and Chang (1988)argued that when equatorial waves propagate zonally,the zonal wavenumber change must satisfy the following condition:

where ωris the modal frequency in a frame of reference where¯u=0.Figure 5 shows the relationship between group velocity and the zonal wavenumber of equatorial Rossby waves.The group velocity is zero when n=3 (n is the latitudinal nodal number for the equatorially trapped waves)and k=6,negative(westward propagating)when k=4(A),and positive(eastward propagating)when k=8(B).Equation(9)illustrates that when equatorial waves reach areas where d¯u/dx<0, then dk/dt>0,i.e.,the zonal wavenumber increases. For long waves with k=4,increases in zonal wavenumber will lead to decreases in westward group velocity. For short waves with k=8,increases in zonal wavenumber will also lead to decreases in the eastward group velocity.Therefore,no matter what the initial wavenumber of the equatorial Rossby wave,its group velocity change will always depend on the sign of the zonal basic flow stretching.Areas where d¯u/dx<0 behave like a natural buffer zone,where equatorial wave energy propagation will slow down.

Fig.5.The group velocity of equatorially trapped Rossby waves for n=1,2,3,4,5.The line perpendicular to the abscissa at k=6 demarks the Cg=0 point for the n= 3 mode.Regions of positive and negative group velocity are noted.The points A and B are the same except that k =4 and k=8,respectively.[Source:Webster and Chang (1988)].
Based on the studies of Whitham(1965)and Bretherton and Garrett(1968),the wave-activity density along the propagation path in slowly varying basic flow is conserved,i.e.,
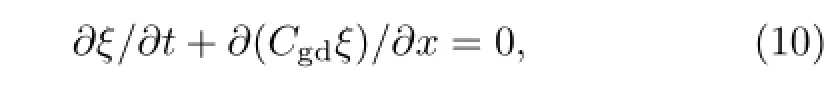
where ζ= ε/ωris the wave-activity density,ε= ρgh2/2 is the wave energy density,and Cgd=¯u+c is the local Doppler velocity during wave propagation. The parameters ζ and ε both reflect wave energy,but the former represents the average wave energy under a specific frequency while the latter represents total wave energy.Webster and Chang(1988)obtained the following equation:

and suggested that the negative stretching deformation of the zonal mean flow,i.e.,d¯u/dx<0,and the
zero Doppler group velocity Cgdfor the zonal propagation of the equatorial wave at one specific location, within the area d¯u/dx<0,are two important conditions for energy accumulation.When an equatorial Rossby wave reaches a location within d¯u/dx<0,the wave propagation begins to slow down.At the time when the Doppler group velocity Cgdreduces to zero at a certain location within the area d¯u/dx<0,the wave energy density ε will increase exponentially according to Eq.(11).That is to say,zonally propagating wave energy will accumulate rapidly in this region.Webster and Chang(1988)named such a region as the energy accumulation region.Apparently,the largest energy accumulation rate occurs where(d¯u/dx|max)<0.For a simple zonal basic flow with a sinusoidal pattern,the largest energy accumulation rate occurs at the point ¯u=0,i.e.,to the east of the maximum westerly wind.
Webster and Chang(1988)and Chang and Webster(1990,1995)subsequently conducted numerous numerical experiments and confirmed that the results were consistent with those of theoretical analysis.No matter where the initial perturbation originates in the tropics,the PKE transported via equatorial wave propagation always accumulates where d¯u/dx< 0. In addition,they found that areas of PKE accumulation are also areas of wave emanation from the tropics to the mid and high latitudes.Thus,tropical convective PKE is first transported to locations within d¯u/dx<0 via Rossby wave propagation and accumulation.Then,perturbation wave trains emanate from the energy accumulation region to high latitudes,realizing atmospheric interaction between the tropics and extratropics. There appear to be two phases of tropical-extratropical teleconnection:first, through the zonal teleconnection along the equator, and then the meridional teleconnection through meridional wave emanation.This explains why there tend to be geographically fixed modal patterns in the extratropical responses to tropical disturbance,i.e.,the extratropical responses are relatively insensitive to the location of the tropical forcing(Branstator,1983;Simmons et al.,1983;Geisler et al.,1985;O'Lenic et al., 1985;Ting and Yu,1998;Zhou et al.,2012).
Using the ray-tracing method,Chang and Webster(1990)found that the energy accumulation process can be divided into forward and backward accumulation.In general,forward accumulation happens when a long Rossby wave propagates westward and reaches the energy accumulation area.However, short Rossby waves tend to be sensitive to their initial location;when located to the east of the maximum westerly wind speed or critical latitude,backward accumulation happens,and vice versa.Mixed Rossby-gravity waves often experience backward accumulation,whereas non-dissipative Kelvin waves often possess high phase speed and thus energy accumulation does not happen easily.
Figure 6 is a schematic diagram showing the energy accumulation-wave train emanation process.In La Ni˜na and El Ni˜no years,the location and intensity of the westerly wind belt in the equatorial upper troposphere change significantly.During La Ni˜na years (Fig.6a),the central-eastern Pacific is an area of large energy accumulation and wave train emanation.In El Ni˜no years(Fig.6b),however,large energy accumulation and wave train emanation occurs in the up-
per levels over the tropical Atlantic.In addition,the upper atmosphere over Indonesia is another region of distinct energy accumulation and wave emanation.

Fig.6.Schematic diagrams showing the impact of different basic states on the locations of the emanations to higher latitudes.The two panels are similar to the situation for(a)La Ni˜na and(b)El Ni˜no.The broad arrows indicate regions of transient accumulation along the equator and transient emanation to higher latitudes.The shaded regions refer to the equatorial easterlies.[Source:Chang and Webster(1990)].
Many advancements have been made in recent years in the study of energy accumulation-wave emanation theory.It has been found that the extratropical atmospheric response to equatorial diabatic heating anomalies is closely related to the basic state structure(Ting and Sardeshmukh,1993;Ting,1996; Zheng et al.,2013;Tan et al.,2015).In addition,Kuo et al.(2001)found that,under a linear assumption, energy mainly accumulates via zonal advection.If the effects of diabatic heating are not considered,the accumulated energy will gradually dissipate by friction. However,under a nonlinear assumption,energy accumulation is maintained through the contraction of the scale of perturbation waves.For example,in the NH summer,westerly wind dominates west of the northwestern Pacific,while easterly wind dominates over the east,which makes it easy to satisfy the condition du/dx<0 in the northwestern Pacific.When tropical perturbations pass by the area of du/dx<0,they may accumulate energy via scale contraction.Kuo et al.(2001)suggested that the energy accumulation in the northwestern Pacific actually provides the initial perturbation vorticity for the formation of tropical cyclones,which is consistent with the conclusions of Holland(1995)and Sobel and Bretherton(1999),in that wave energy accumulation provides favorable conditions for the genesis of tropical cyclones over the western Pacific.Using reanalysis data,Tam and Li(2006) investigated the formation of synoptic-scale perturbation in the western Pacific and found that the accumulation of perturbation energy due to zonal scalecontraction is more important than that due to zonal flow advection.Based on energy accumulation theory,Done et al.(2011)investigated the relationship between easterly waves in the tropical Atlantic and hurricane formation.Chen et al.(personal communication,2014)discussed the impact of monsoon troughs over the South China Sea on the genesis of tropical cyclones.In addition,many researchers have tried to explain the mechanisms involved in the formation,variation,and distribution of the South Pacific convergence zone(SPCZ),using energy accumulation-wave emanation theory.These studies have revealed that areas near the SPCZ meet the condition of du/dx<0,and are thus conducive to energy accumulation.The orientation of the SPCZ also suggests the existence of energy transport from the tropics to midlatitudes in the SH(Widlansky et al.,2011).
5.Equatorial wave lateral expansion theory
A key characteristic of energy accumulation-wave emanation theory is that the midlatitude atmospheric response to tropical forcing always occurs on both sides of the energy accumulation region. However, the transitional process from energy accumulation to wave emanation is not entirely clear.For example, the initial meridional group velocity is zero when the equatorial waves are triggered by the tropical forcing; however,when waves emanate from the energy accumulation region,their meridional group velocity is apparently non-zero.One possible mechanism for the formation of the new wave trains may be nonlinear wave-wave interaction.However,Chang and Webster (1990,1995)indicated that linear and nonlinear processes are rather similar.In other words,wave emanation can be realized under a linear assumption,without the nonlinear wave-wave interaction in the energy accumulation area.What,therefore,is the mechanism behind the transport of PKE from the tropics to the midlatitudes,which often results in geographically fixed modal responses?
In their study of the teleconnection between tropical perturbation and global climate,Lau and Lim (1984)proposed that equatorial Rossby waves can affect atmospheric activity in the midlatitudes only if they are located in the equatorial westerly wind belt. Wilson and Mak(1984)investigated the impact of midlatitude atmospheric activity on tropical weather and climate.They found that equatorial Rossby waves can experience“trapping”when they propagate in a zonally sheared basic flow.That is to say,in addition to the zonal stretching deformation,zonal shear in the basic flow can also affect the propagation of Rossby waves.Zhang and Webster(1989)considered the eff-
ect of shear in the basic flow,and obtained the general expression for a wave equation:

where Γ2(y)is the square of refractive index,which is widely applied in the study of planetary wave propagation(Bennett and Young,1971;Wilson and Mak, 1984).Generally,when Γ2(y)>0,V(y)yields a wave solution;when Γ2(y)<0,V(y)attenuates.For an equatorially trapped wave,it needs to satisfy the following condition:

where ytis the turning latitude for the equatorially trapped wave.When y<yt,V(y)yields a wave solution;when y>yt,V(y)attenuates and disappears.A larger turning latitude indicates a wider range of latitudes under the influence of the trapped waves,and is thus more conducive to interaction between the tropics and midlatitudes.
Zhang and Webster(1989)suggested that the shear effects of zonal flow would increase the turning latitude to some degree.They explained that this is possibly because the shear effects of zonal flow increases the north-south geopotential gradient,thus intensifying the β effect and resulting in a decrease in the“trapping”of equatorial waves.There is no significant difference between the turning latitude in easterly and westerly sheared flows for eastward propagating Kelvin waves,gravity waves,or westward propagating mixed Rossby-gravity waves.However,the turning latitude for westward-propagating equatorial Rossby waves is much larger in sheared westerlies than in sheared easterlies,while the turning latitude for westward-propagating gravity waves is larger in sheared easterlies than in sheared westerlies.Hence, on the timescale of tropical convection,the transient gravity waves triggered by latent heat release in the zonally sheared easterly wind belt are more able to affect the mid-high latitudes. In contrast,on the timescale of Rossby waves(i.e.,synoptic and lowfrequency timescales),interaction between the lowand midlatitudes is mainly realized through westwardpropagating Rossby waves in zonally sheared westerly wind.

Fig.7.Distribution of the turning latitude of an equatorially trapped Rossby wave in the two-dimensional basic boreal winter 200-hPa zonal flow.The letters X and Y denote forcing locations.Forcing located at X where y>ytwill not project significantly on equatorially trapped waves.Forcing located at Y where y<ytwill force trapped waves.[Source: Zhang and Webster(1989)].
In a certain sense,an increase in the turning latitude of equatorial waves represents the lateral expansion of equatorial waves.Figure 7 is a schematic diagram showing the propagation of Rossby waves in sheared zonal flow.The thick dotted line indicates the range of Rossby wave expansion at various longitudes.For an initial perturbation in the midlatitudes, when the perturbation is located at X,the perturbation cannot directly affect the tropics,since y>yt.
However,if the perturbation is located at Y,where y<yt,it will be able to affect the tropics through the zonal propagation of equatorial waves.In other words, the expansion of equatorial waves not only enables tropical forcing to influence the midlatitudes,but also causes midlatitude perturbations to affect the tropics.Zhang and Wesbter(1989)pointed out that the impact of tropical forcing on the mid-high latitudes is not necessarily realized through the emanation of wave trains from the equatorial westerly wind belt. Instead,the interaction between the tropics and extratropics is more like a wave“expansion”phenomenon. Equatorial Rossby waves propagate zonally and reach the equatorial westerly wind belt area.Meanwhile, changes in the zonal basic flow result in a rapid increase in their turning latitude.When the turning latitude becomes sufficiently large,the tropical influence will reach the temperate zone.
It is worth noting that the importance of equatorial wave lateral expansion theory needs more attention.In fact,equatorial wave lateral expansion theory is consistent with energy accumulation-wave emanation theory.They both explain the atmospheric interaction between tropical perturbations and midlatitude activity from different perspectives.Since energy accumulation theory has a solid mathematical basis to support its framework,people tend to apply this theory more than others when explain lowand mid-latitude interaction.However,as mentioned previously,under energy accumulation theory,equatorial waves need to transfer from having zonal group speed only to having meridional group speed only; however,the process of transition is not clear.Equatorial wave lateral expansion theory overcomes this problem in energy accumulation-wave emanation theory,and can explain the two-way interaction between the tropics and temperate zone well,without introducing new wave trains.Additional theoretical studies and verification of numerical experiments are required for equatorial wave lateral expansion theory to further progress.
6.Meridional basic flow theory
A common feature among the previously introduced energy propagation theories is that the meridional propagation of Rossby waves can only be realized in the zonal mean westerly wind belt.For example, Rossby waves can propagate equatorward and poleward according to great circle theory,but its propagation will be constrained once it reaches the critical latitude.Similarly,under westerly duct theory,the westerly wind belt over the tropical eastern Pacific and Atlantic behaves like a“bridge”for the interaction between the tropics and temperate zone.According to these theories,large areas in the low latitudes are under the control of easterly winds in the NH summer, and hence the atmospheric activity in the NH and SH would be independent of one another.
However,many studies have revealed that distinct links exist between the two hemispheres,even in the NH summer.For example,Lu(1987)found that summertime SST anomalies in the tropical western Pacific affect the atmospheric circulation of the NH through Pacific-Japan waves.He(1989)investigated the influence of SH 40-day quasi-oscillation on the summer monsoon in the NH,and suggested that the meridional propagation of this perturbation is a possible mechanism for interaction between the two hemispheres. In recent years,links between anomalous atmospheric circulation in the SH and weather and climate change in East Asia have attracted great attention.Studies have shown that changes in the circulation of the SH are closely related to the East Asian summer monsoon,and precipitation anomalies in South and North China,as well as dust storm occurrence in northern China(Shi et al.,2001;Zeng and Li,2002;Nan and Li,2005;Fan and Wang,2006;Song and Li,2009). However,questions remain unanswered as to how the atmospheric interactions between the SH and NH are realized.Fan and Wang(2006)argued that the interaction between the two hemispheres is possibly related to the meridional teleconnection of barotropic waves in the high latitudes of the SH and coastal regions of East Asia.In addition,many studies have revealed that Hadley circulation plays a critical role in the meridional propagation of stationary waves(Watterson and Schneider,1987;Ji,1990;Krishnamurti et al.,1997; Esler et al.,2000;Ji et al.,2014).
Li and Li(2012)and Li et al.(2015)studied
the interaction between the two hemispheres over the Asian-Australian monsoon region,with a focus on the effects of meridional basic flow on the quasi-stationary wave propagation in easterly basic flow.Under the assumption of uneven horizontal flow,they obtained the frequency spectrum expression
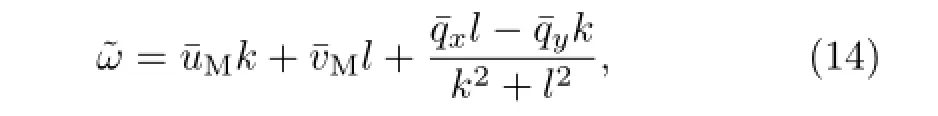

Figure 8 shows the wave ray-tracing results.Figures 8a and 8b present the prescribed distribution of the zonal and meridional basic flows,respectively.Figure 8c shows that no matter where the initial perturbation is located,perturbation waves propagate equatorward and poleward when only the zonal basic flow is considered.The poleward-propagating wave turns equatorward after it reaches the turning latitude,and is eventually trapped at the critical latitude.This is consistent with results from previous studies in that stationary waves cannot propagate in easterly wind belts in a zonally symmetric zonal flow basic state. Figures 8d and 8e show the situation when the meridional basic flow is considered.Large changes occur in the perturbation propagation under this condition.In Fig.8d,the initial perturbation is located in the NH. The results indicate that in strong northerly winds, the perturbation can cross the weak tropical easterly wind belt and propagate to the mid-high latitudes of the other hemisphere.On the other hand,when the initial perturbation is located in the SH(Fig.8e), the equatorward propagation of perturbation is still constrained.Li and Li(2012)and Li et al.(2015) conducted numerous experiments to confirm that the propagation of such a perturbation type is one directional,and the propagation direction depends on the direction of the meridional basic flow.For example,if the background basic flow is in the form of northerly wind,then the meridional group speed of NH stationary waves intensifies,which is conducive to crossequatorial wave propagation.In contrast,the meridional group velocity of the stationary waves in the SH decreases.Thus,northward propagation of SH perturbations is constrained.The opposite is true when the background basic flow is in the form of southerly wind.Under this situation,perturbations in the SH can propagate to the NH,while the equatorward propagation of perturbations in the NH is limited.

Fig.8.Stationary wave-ray paths and propagation distance in(a)zonal symmetric flow,(b)non-uniform basic flow, with sources at(c)(30°N,0°),(30°S,0°),(d)(30°N,0°),and(e)(30°S,0°),marked every two days.The numbers indicated in the figures denote the zonal wave numbers.[Source:Li and Li(2012)].
Meridional basic flow theory overcomes the problem in the current theory of planetary wave propagation,which considers zonally symmetric basic flow and cannot explain the interaction between easterly and westerly winds.Meridional basic flow theory proposes that meridional basic flow enables stationary waves to cross the easterly wind belt and propagate between the two hemispheres.Compared to traditional wave propagation theory,meridional basic flow theory considers a more realistic background flow.The new concept that stationary waves can overcome the constraints of critical latitudes and propagate to the other hemisphere is helpful for a better understanding of teleconnection patterns.Using reanalysis data,Li and Li(2012)and Li et al.(2015)analyzed the global teleconnection patterns in the upper troposphere streamfunction field during the NH summer.They found teleconnection patterns between northern and southern Africa and the southern Indian Ocean and Antarctic,as well as between Hawaii and the southern Pacific and Atlantic.Based on horizontal wave ray-tracing in a zonally asymmetric flow,they proposed that the energy dispersion during barotropic Rossby wave propagation is a possible reason for the formation of teleconnection in these wave trains.
Presently,there are two theoretical explanations for cross-equatorial teleconnection patterns.Sardeshnukh and Hoskins(1988)provided an explanation in which it was suggested that heating could result in a Rossby wave source in extratropical westerly wind belts,and then further trigger the Rossby waves. The other explanation is based on stationary Rossby wave propagation theory.When stationary Rossby waves cross the tropical easterly wind belt and propagate from one hemisphere to the other,they can lead to teleconnection between the two hemispheres. This theory has been widely applied(Watterson and
Schneider,1987;Ji,1990;Krishnamurti et al.,1997; Fan and Wang,2006).Meridional basic flow theory provides a theoretical basis for cross-equatorial wave propagation.
7.Diagnosis of energy propagation and waveflow interaction
In atmospheric wave dynamics,wave-mean flow interaction is an important topic. In early work, Rossby(1939)discussed the relationship between zonal basic flow and stationary waves in the midlatitudes.He found that the Aleutian low shifted westward when the basic flow was weak,and vice versa. In addition,Charney and Stern(1962)investigated the link between the vertical propagation of quasistationary waves and upper-level jet streams.They found that a meridional temperature gradient of zero at the surface is a prerequisite for maintaining a stable upper-level jet stream,and identified the rapid outbreak of the polar night jet in the NH winter as a good example of such a baroclinic instability type.They suggested that this is possibly related to the downward propagation of unstable perturbations at the height of 30 km,accompanied by conversion between kinetic and potential energy.These are classic studies of wavemean flow interaction.
Before the 1960s,most diagnostic analyses of wave-mean flow interaction were based on eddy heat and momentum flux diagnosis.Charney and Drazin (1961)proposed the concept of wave refraction in their study of the vertical propagation of planetary waves. Waves can propagate over areas where the refractive index is real,while they will be reflected in areas where the refractive index is imaginary.Therefore, the path and coverage area of wave propagation can be diagnosed based on the spatial distribution of the wave refraction index.In addition,another important diagnostic quantity,the Eliassen-Palm(EP)flux (Eliassen and Palm,1961),was proposed.The EP flux is a two-dimensional wave activity flux that includes both the heat and momentum fluxes,expressed as F={F(y),F(p)},where The overbars and primes indicate the zonal average and zonal deviation of the variable;u,v,and w are the zonal,meridional,and vertical winds,respectively; and θ is the potential temperature.There are several advantages to using EP flux.For example,it can diagnose heat and momentum fluxes simultaneously.In the y−z plane,the EP flux divergence indicates the northward transport of quasi-geostrophic perturbation potential vorticity flux,and vice versa.However,in a sheared flow,wave energy is not conserved.Using the potential vorticity equation,Andrews and McIntyre(1976,1978)introduced the concept of“residual meridional circulation”and the wave activity conservation equation:



EP flux is one of the most important tools for the study of small-amplitude wave-mean flow interaction.In the area of EP flux convergence,waves develop and basic flow decelerates,and vice versa.Therefore, EP flux has been widely used in studies of vertical wave propagation,wave-mean flow interaction,quasibiennial oscillation of stratospheric winds,and sudden stratospheric warming(Lindzen and Holton,1968; Dickinson,1969;Holton and Lindzen,1972;Dunkerton and Baldwin,1991;Limpasuvan et al.,2004).The original EP flux formulation was developed for the case of wave perturbation superimposed on the zonally averaged mean flow,which greatly simplifies the mathematical formula.However,we are more concerned with Rossby wave propagation in three-dimensional space,which cannot be described by the traditional EP flux formulation.
Hoskins et al.(1983)studied the interaction between transient waves and basic flows using a time-

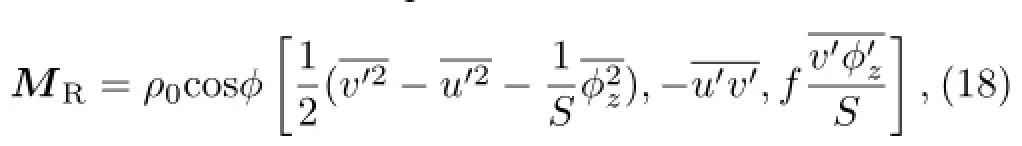
where MRis the wave activity flux,whose direction–and the direction of the relative wave group velocity–forms an angle.Similarly,▽·MRcan also indicate sources and sinks of transient wave activity.Compared to EH,there is one extra baroclinic term in the x-direction for MR.Plumb(1986)explained that under certain conditions,the baroclinic term would become large enough to change the sign of MRin the x-direction.MRcan be applied in a quasi-geostrophic baroclinic atmosphere,and in a slowly varying basic mean flow.In the same year,Trenberth(1986)defined a transient wave activity flux in his study of blocking in the SH,which is expressed as
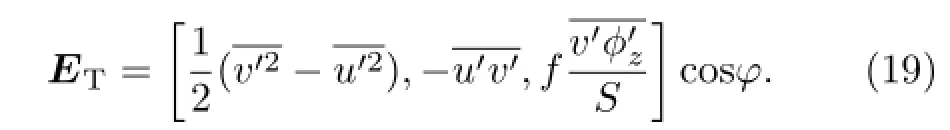
Compared to EHand MR,ETis parallel to the direction of the group velocity of the transient waves.EThas the same diagnostic capability of EHand MRbut with a simpler form.It can be used in a nongeostrophic atmosphere,and thus has been widely applied in the study of transient Rossby waves.
In addition,greatadvancementshavebeen achieved in the diagnostic study of stationary Rossby wave propagation.Plumb(1985)first explored the conservation relationship that needs to be satisfied during the propagation of small-amplitude stationary waves in a zonally uniform basic flow.He provided the three-dimensional Rossby wave activity flux Fs.Fsis parallel to the group velocity direction of the stationary waves and represents the direction of energy propagation.By calculating the divergence of wave activity flux,we can determine the sources and sinks of the stationary waves(Plumb,1986;Karoly et al., 1989).Since Plumb(1985)only considered the zonally uniform basic flow and small amplitude perturbation,many researchers expanded his study to obtain more realistic stationary wave activity flux in real atmosphere(Kuroda,1996).For example,Takaya and Nakamura(1997,2001)developed an expanded version of the Plumb equation(Plumb,1985)for the wavy basic flow that better represents the situation in the real atmosphere.
In recent years,substantial progress has been made in the diagnostic study of inertia-gravity waves and Kelvin waves.For example,Miyahara(2006)established a three-dimensional wave activity flux equation appropriate for inertia-gravity waves in timeaveraged Boussinesq flow. Based on the theory of small-amplitude waves in a slowly varying mean flow and the primitive equations,Kinoshita et al.(2010) and Kinoshita and Sato(2013a,b)derived a wave activity flux equation that is similar to the threedimensional Stokes drift.They suggested that this three-dimensional wave activity flux equation is appropriate for both inertia-gravity waves and Rossby waves.In addition,Kinoshita and Sato(2014)obtained a suite of equations in the equatorial β plane, which can be easily applied for diagnostic analysis of the interaction between Kelvin waves and the basic flow.This is important for studying equatorial quasibiennial oscillation and semi-annual oscillation.
It is worth noting that researchers in China have contributed greatly to the study of wave-mean flow interaction. For example,Huang(1983)expanded the EP flux formulation to spherical coordinates,suggesting that quasi-stationary planetary waves often split into two branches during their propagation in a three-dimensional spherical atmosphere.This result confirmed the conservation law of spherical planetary wave actions.Wu and Chen(1989)further advanced EP flux diagnostics by applying it to moist atmosphere,which greatly expanded the possibilities for EP flux application.In studying upper-tropospheric wave-mean flow interaction,Gao et al.(1990)and Ran et al.(2005)expanded the EP flux formula to a baroclinic atmosphere and proposed a generalized EP
EP flux formulation that can better explain the significant acceleration that sometimes occurs in the uppertropospheric jet stream.
8.Summary and discussion
This paper reviews and summarizes theoretical studies of energy propagation and atmospheric interaction between different latitudes.Diagnostic studies of energy propagation and wave-mean flow interaction are also discussed.The following key components and findings are covered within the paper:
(1)Great circle theory explains the stationary Rossby wave propagation in a spherical atmosphere. Rossby wave energy dispersion theory can successfully explain the links between the atmospheric activity at different latitudes.
(2)Westerly wind duct theory indicates that the mean zonal westerly wind belt in the upper troposphere over the equatorial central-eastern Pacific and the Atlantic is a“corridor”for atmospheric interaction between the two hemispheres.The perturbation waves triggered in the midlatitudes can cross the equator and propagate to the other hemisphere through the“westerly duct”.The efficiency of the cross-equatorial propagation depends on the zonal scale of the perturbation waves relative to the“westerly duct”and the intensity of the zonal westerly wind.
(3)Energy accumulation-wave emanation theory suggests that negative stretching deformation of the basic zonal flow can cause accumulation of perturbation energy.Tropical perturbations first reach certain regions through the zonal transport of equatorial waves,wherein wave energy accumulates and then affects midlatitude activity by means of wave emanation.
(4)Equatorial wave lateral expansion theory discusses the possible mechanisms behind the interaction of the tropics and temperate zone from the perspective of turning latitudes of equatorial waves.Since the turning latitude is large for westward-propagating Rossby waves in the sheared westerly wind belt,equatorial waves will experience“expansion”when they reach this latitude.As a result,tropical perturbations can affect midlatitude regions and there is a two-way interaction between the tropics and midlatitudes.
(5)Meridional basic flow theory considers the impact of meridional mean flow on the meridional propagation of stationary waves.Certain meridional mean flows play a critical role in the propagation of stationary waves from one hemisphere to the other.This theory is important for understanding the connection between the activity in the two hemispheres,especially the energy exchange between the two hemispheres in the Australian-Asian monsoon region.
(6)Diagnostic methods for wave-mean flow interaction have been advancing over the years,from the simple calculation of heat and momentum fluxes in early work,to the development of EP flux and threedimensional wave action flux in subsequent studies.In recent years,important progress has been made in the study of wave conservation and wave activity fluxes for inertia-gravity waves and equatorial Kelvin waves.
From the 1940s to the present day,continuous efforts have been made to study the energy propagation and atmospheric interaction between different latitudes.The continued development and improvement of energy propagation theory has helped answer many scientific questions and deepened our understanding of atmospheric teleconnections.
In the context of global warming,large-scale atmospheric circulation has been changing.For example,Held and Soden(2006),Vecchi and Soden(2007), and Tokinaga et al.(2012)all found that the intensity of the Walker and Hadley circulations has decreased under global warming.In contrast,Meng et al.(2012), Wang et al.(2013),and England et al.(2014)argued that the Walker and Hadley circulations have intensified.These conflicting results indicate that changes in large-scale circulation against the global warming background might be complicated,and these changes will inevitably lead to climate anomalies in many regions throughout the world.Lu et al.(2007)found that the Hardly circulation has shifted northward,resulting in a northward shift of dry regions in the extratropics.Williams and Funk(2011)also suggested that the westward shift of Hardly circulation is one reason for the drought anomalies in East Africa.As the two
most important zonal and meridional circulation patterns in the atmosphere,changes in the Hadley and Walker circulations directly affect basic mean flows in the zonal and meridional directions,and thus influence the cross-equatorial propagation of perturbations and the interactions between the mid and low latitudes.In addition,while energy propagation theories qualitatively describe the interactions between the atmospheric activity at different latitudes,we are more concerned about quantitatively analyzing these interactions,and determining to what extent the activity in one region affects that in other regions.Finally,another important question is:how does one apply these theories in practical numerical weather prediction and in improving the accuracy of weather forecasts?The above theoretical analyses have shown that perturbation propagations are sensitive to changes in basic flow.Hence,one important issue in modeling studies is how to precisely simulate changes in basic flow,especially the distribution of basic flow in the tropical upper troposphere.From the perspective of perturbation propagation,it is necessary to improve the prediction of basic flow for the purpose of improving weather and climate prediction.This is a challenging issue facing the numerical modeling community in the coming years.
Acknowledgments.We appreciate the suggestions and comments from three anonymous reviewers, which are helpful for improving the overall quality of the article.
Ambrizzi,T.,B.Hoskins,and H.-H.Hsu,1995:Rossby wave propagation and teleconnection patterns in the austral winter.J.Atmos.Sci.,52,3661–3672.
Andrews,D.G.,and M.E.McIntyre,1976:Planetary waves in horizontal and vertical shear:The generalized Eliassen-Palm relation and the mean zonal acceleration.J.Atmos.Sci.,33,2031–2048.
Andrews,D.G.,and M.E.McIntyre,1978:Generalized Eliassen-Palm and Charney-Drazin theorems for waves on axismmetric mean flows in compressible atmospheres.J.Atmos.Sci.,35,175–185.
Arkin,P.A.,1982:The relationship between interannual variability in the 200-mb tropical wind field and the Southern Oscillation.Mon.Wea.Rev.,110,1393–1404.
Arkin,P.A.,and P.J.Webster,1985:Annual and interannual variability of the tropical-extratropical interaction:An empirical study.Mon.Wea.Rev., 113,1510–1523.
Baldwin,M.P.,L.J.Gray,T.J.Dunkerton,et al.,2001: The quasi-biennial oscillation.Rev.Geophys.,39, 179–229.
B´eland,M.,1976: Numerical study of the nonlinear Rossby wave critical level development in a barotropic zonal flow.J.Atmos.Sci.,33,2065–2078.
Bennett,J.R.,and J.A.Young,1971:The influence of latitudinal wind shear upon large-scale wave propagation into the tropics.Mon.Wea.Rev.,99, 202–214.
Bolin,B.,1950:On the influence of the earth's orography on the general character of the westerlies.Tellus,2, 184–195.
Branstator,G.,1983:Horizontal energy propagation in a barotropic atmosphere with meridional and zonal structure.J.Atmos.Sci.,40,1689–1708.
Bretherton,F.P.,and C.J.R.Garrett,1968:Wavetrains in inhomogeneous moving media.Proc.Roy.Soc. London,302,529–554.
Brunet,G.,and P.H.Haynes,1996:Low-latitude reflection of Rossby wave trains.J.Atmos.Sci.,53, 482–496.
Bjerknes,J.,1966:A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature.Tellus,18,820–829.
Chao Jiping,1977:On the large-scale interactions of sea and atmosphere and long-range weather forecasts. Chinese J.Atmos.Sci.,1,223–233.(in Chinese)
Charney,J.G.,1947:The dynamics of long waves in a baroclinic westerly current.J.Meteor.,4,135–162.
Charney,J.G.,and A.Eliassen,1949:A numerical method for predicting the perturbations of the middle latitude westerlies.Tellus,1,38–54.
Charney,J.G.,and P.G.Drazin,1961:Propagation of planetary-scale disturbances from the lower into the upper atmosphere.J.Geophys.Res.,66,83–109.
Charney,J.G.,and M.E.Stern,1962:On the stability of internal baroclinic jets in a rotating atmosphere. J.Atmos.Sci.,19,159–172.
Charney,J.G.,1963:A note on the large-scale motions in the tropics.J.Atmos.Sci.,20,607–609.
Charney,J.G.,1969:A further note on large-scale motions in the tropics.J.Atmos.Sci.,26,182–185.
Chang,H.-R.,and P.J.Webster,1990:Energy accumulation and emanation at low latitudes.Part II: Nonlinear response to strong episodic equatorial forcing.J.Atmos.Sci.,47,2624–2644.
Chang,H.-R.,and P.J.Webster,1995:Energy accumulation and emanation at low latitudes.Part III: Forward and backward accumulation. J.Atmos. Sci.,52,2384–2403.
Chen,W.,S.Yang,and R.-H.Huang,2005:Relationship between stationary planetary wave activity and the East Asian winter monsoon.J.Geophys.Res.,110, D14110,doi:10.1029/2004JD005669.
Dickinson,R.E.,1968:Planetary Rossby waves propagating vertically through weak westerly wind wave guide.J.Atmos.Sci.,25,981–1002.
Dickinson,R.E.,1969:Theory of planetary wave-zonal flow interaction.J.Atmos.Sci.,26,73–81.
Dickinson,R.E.,1970:Development of a Rossby wave critical level.J.Atmos.Sci.,27,627–633.
Ding,Q.H.,and B.Wang,2005:Circumglobal teleconnection in the Northern Hemisphere summer.J. Climate,18,3483–3505.
Ding,Q.H.,J.M.Wallace,D.S.Battisti,et al.,2014: Tropical forcing of the recent rapid Arctic warming in northeastern Canada and Greenland. Nature, 509,209–212.
Ding Yihui,2009:Physical problems in the global climate change.Physics,38,71–83.(in Chinese)
Done,J.M.,G.J.Holland,and P.J.Webster,2011:The role of wave energy accumulation in tropical cyclogenesis over the tropical North Atlantic.Climate Dyn.,36,753–767.
Dunkerton,T.J.,and M.P.Baldwin,1991:Quasibiennial modulation of planetary-wave fluxes in the Northern Hemisphere winter.J.Atmos.Sci.,48, 1043–1061.
Eady,E.T.,1949:Long waves and cyclone waves.Tellus, 1,33–52.
Edmon,H.J.Jr.,B.Hoskins,and M.E.McIntyre,1980: Eliassen-Palm cross-sections for the troposphere.J. Atmos.Sci.,37,2600–2617.
Eliassen,A.,and E.Palm,1961:On the transfer of energy in stationary mountain waves.Geophys.Publ., 22,1–23.
England,M.H.,S.McGregor,P.Spence,et al.,2014: Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus.Nat. Climate Change,4,222–227.
Enomotol,T.,B.J.Hoskins,and Y.Matsuda,2003:The formation mechanism of the Bonin high in August. Quart.J.Roy.Meteor.Soc.,129,157–178.
Esler,J.G.,L.M.Polvani,and R.A.Plumb,2000:The effect of a Hadley circulation on the propagation and reflection of planetary waves in a simple one-layer model.J.Atmos.Sci.,57,1536–1556.
Fan Ke and Wang Huijun,2006:Studies of the relationship between the Southern Hemispheric atmospheric circulation and climate over East Asia.Chinese J. Atmos.Sci.,30,402–412.(in Chinese)
Gao Shouting,Tao Shiyan,and Ding Yihui,1990:The generalized E-P flux of wavemeanflow interactions. Sci.China(Chem.),33,704–715.
Geisler,J.E.,and R.E.Dickinson,1975:Critical level absorption of barotropic Rossby waves in a northsouth flow.J.Geophys.Res.,80,3805–3811.
Geisler,J.E.,M.L.Blackmon,G.T.Bates,et al.,1985: Sensitivity of January climate response to the magnitude and position of equatorial Pacific sea surface temperature anomalies.J.Atmos.Sci.,42,1037–1049.
Gill,A.E.,1980:Some simple solutions for heat-induced tropical circulation.Quart.J.Roy.Meteor.Soc., 106,447–462.
Grose,W.L.,and B.J.Hoskins,1979:On the influence of orography on large-scale atmospheric flow. J. Atmos.Sci.,36,223–234.
He Jinhai,1989:Talk about the mechanism of propagation of quasi-40-day oscillation.J.Nanjing Ins. Meteor.,3,239–248.(in Chinese)
Held,I.M.,and B.J.Soden,2006:Robust responses of the hydrological cycle to global warming.J.Climate,19,5686–5699.
Hirota,I.,1978:Equatorial waves in the upper stratosphere and mesosphere in relation to the semiannual oscillation of the zonal wind.J.Atmos.Sci.,35, 714–722.
Holland,G.J.,1995:Scale interaction in the western Pacific monsoon.Meteor.Atmos.Phys.,56,57–79.
Holton,J.R.,and R.S.Lindzen,1972:An updated theory for the quasi-biennial cycle of the tropical stratosphere.J.Atmos.Sci.,29,1076–1080.
Holton,J.R.,1979:An Introduction to Dynamic Meteorology.2nd Ed.,Academic Press,New York,319 pp.
Horel,J.D.,and J.M.Wallace,1981:Planetary-scale atmospheric phenomena associated with the Southern Oscillation.Mon.Wea.Rev.,109,813–829.
Hoskins,B.J.,A.J.Simmons,and D.G.Andrews, 1977:Energy dispersion in a barotropic atmosphere. Quart.J.Roy.Meteor.Soc.,103,553–567.
Hoskins,B.J.,and D.J.Karoly,1981:The steady linear response of a spherical atmosphere to thermal and orographic forcing.J.Atmos.Sci.,38,1179–1196.
Hoskins,B.J.,I.N.James,and G.H.White,1983: The shape,propagation and mean-flow interaction of large-scale weather systems.J.Atmos.Sci.,40, 1595–1612.
Hoskins,B.J.,and T.Ambrizzi,1993:Rossby wave propagation on a realistic longitudinally varying flow.J. Atmos.Sci.,50,1661–1671.
Huang Ronghui,1983:The role of Greenland Plateau in the formation of the Northern Hemispheric stationary planetary waves in winter.Chinese J.Atmos. Sci.,7,393–402.(in Chinese)
Jaw,J.-J.,1946: The formation of the semipermanent centers of action in relation to the horizontal solenoidal field.J.Meteor.,3,103–114.
Ji Jingjun,1990:Influences of atmospheric meridional circulation on propagation of the planetary wave and energy transport.Chinese J.Atmos.Sci.,14, 413–421.(in Chinese)
Ji,X.,J.D.Neelin,S.-K.Le,et al.,2014:Interhemispheric teleconnections from tropical heat sources in intermediate and simple models.J.Climate,27, 684–697.
Jin,F.-F.,1997a:An equatorial ocean recharge paradigm for ENSO.Part I:Conceptual model.J.Atmos. Sci.,54,811–829.
Jin,F.-F.,1997b:An equatorial ocean recharge paradigm for ENSO.Part II:A stripped-down coupled model. J.Atmos.Sci.,54,830–847.
Karoly,D.K.,R.A.Plumb,and M.F.Ting,1989: Examples of the horizontal propagation of quasistationary waves.J.Atmos.Sci.,46,2802–2811.
Killworth,P.D.,and M.E.McIntyre,1985:Do Rossbywave critical layers absorb,reflect,or over-reflect? J.Fluid Mech.,161,449–492.
Kinoshita,T.,Y.Tomikawa,and K.Sato,2010:On the three-dimensional residual mean circulation and wave activity flux of the primitive equations. J. Meteor.Soc.Japan,88,373–394.
Kinoshita,T.,and K.Sato,2013a:A formulation of three-dimensional residual mean flow applicable both to inertia-gravity waves and to Rossby waves. J.Atmos.Sci.,70,1577–1602.
Kinoshita,T.,and K.Sato,2013b:A formulation of unified three-dimensional wave activity flux of inertiagravity waves and Rossby waves.J.Atmos.Sci., 70,1603–1615.
Kinoshita,T.,and K.Sato,2014:A formulation of threedimensional residual mean flow and wave activity flux applicable to equatorial waves.J.Atmos.Sci., 71,3427–3438.
Knippertz,P.,2007:Tropical-extratropical interactions related to upper-level troughs at low latitudes.Dyn. Atmos.Oceans,43,36–62.
Krishnamurti,T.N.,C.P.Wagner,T.J.Cartwright,et al.,1997:Wave trains excited by cross-equatorial passage of the monsoon annual cycle.Mon.Wea. Rev.,125,2709–2715.
Kuroda,Y.,1996:Quasi-geostrophic three-dimensional E-P flux of stationary waves on a sphere.J.Meteor. Soc.Japan,74,5563–5569.
Kuo,H.,J.Chen,R.Williams,et al.,2001:Rossby waves in zonally opposing mean flow:Behavior in Northwest Pacific summer monsoon.J.Atmos.Sci.,58, 1035–1050.
Lau,K.-M,and H.Lim,1984:On the dynamics of equatorial forcing of climate teleconnections.J.Atmos. Sci.,41,161–176.
Li Yanjie and Li Jianping,2012:Propagation of planetary waves in the horizontal non-uniform basic flow. Chinese J.Geophys.,55,361–371.(in Chinese)
Li,Y.J.,J.P.Li,F.F.Jin,et al.,2015:Interhemispheric propagation of stationary Rossby waves in a horizontally nonuniform background flow. J.Atmos. Sci.,72,3233–3256.
Limpasuvan,V.,D.W.J.Thompson,and D.L.Hartmann,2004:The life cycle of the Northern Hemisphere sudden stratospheric warmings.J.Climate, 17,2584–2596.
Lindzen,R.S.,and J.R.Holton,1968:A theory of the quasi-biennial oscillation.J.Atmos.Sci.,25,1095–1107.
Liu Shikuo and Tan Benkui,1988a:Nonlinear Rossby waves forced by topography.Appl.Math.Mech.,9, 253–266.
Liu Shikuo and Tan Benkui,1988b:Rossby waves with the change of β.Appl.Math.Mech.,13,39–49.
Liu,Y.Y.,L.Wang,W.Zhou,et al.,2014:Three Eurasian teleconnection patterns: Spatial structures,temporal variability,and associated winter climate anomalies.Climate Dyn.,42,2817–2839.
Longuet-Higgins,M.S.,1964:Planetary waves on a rotating sphere.Proc.Roy.Soc.London,279, 446–473.
Lu,J.,G.A.Vecchi,and T.Reichler,2007:Expansion of the Hadley cell under global warming.Geophys. Res.Lett.,34,L06805.
Lu Peisheng and Zeng Qingcun,1981:On the evolution process of disturbances in the barotropic atmosphere.Chinese J.Atmos.Sci.,5,1–8.(in Chinese)
Lu,R.,1987:Convective activities in the tropical western Pacific and their impact on the Northern Hemisphere summer circulation.J.Meteor.Soc.Japan, 65,373–390.
Maga˜na,V.,and M.Yanai,1991:Tropical-midlatitude interaction on the timescale of 30 to 60 days during the northern summer of 1979.J.Climate,4,180–201.
Mak,M.-K.,1969:Laterally driven stochastic motions in the tropics.J.Atmos.Sci.,26,41–64.
Maruyama,T.,and M.Yanai,1967:Evidence of largescale disturbances in the equatorial lower stratosphere.J.Meteor.Soc.Japan,45,195–196.
Matsuno,T.,1966:Quasi-geostrophic motions in the equatorial area.J.Meteor.Soc.Japan,44,25–43.
Meng,Q.J.,M.Latif,W.Park,et al.,2012:Twentieth century Walker circulation change:Data analysis and model experiments.Climate Dyn.,38,1757–1773.
Miyahara,S.,2006:A three dimensional wave activity flux applicable to inertio-gravity waves.SOLA,2, 108–111.
Murakami,T.,and M.S.Unninayar,1977:Atmospheric circulation during December 1970 through February 1971.Mon.Wea.Rev.,105,1024–1038.
Nan Sulan and Li Jianping,2005:The relationship between the summer precipitation in the Yangtze River valley and the boreal spring Southern Hemisphere annular mode.I:Basic facts.Acta Meteor.Sinica, 63,837–846.(in Chinese)
O'Lenic,E.,P.Webster,and A.Samel,1985:The effect of initial uncertainty in tropical analyses upon fiveday forecasts with NMC's Global Spectral Model. NMC Tech.,Note 311.
Plumb,R.A.,1985:On the three-dimensional propagation of stationary waves. J.Atmos.Sci.,42, 217–229.
Plumb,R.A.,1986:Three-dimensional propagation of transient quasi-geostrophic eddies and its relationship with the eddy forcing of the time-mean flow.J. Atmos.Sci.,43,1657–1678.
Radok,U.,and A.M.Grant,1957:Variations in the high tropospheric mean flow over Australia and New Zealand.J.Meteor.,14,141–149.
Ran Lingkun,Gao Shouting,and Lei Ting,2005:Relation between acceleration of basic zonal flow and EP flux in the upper-level jet stream region.Chinese J. Atmos.Sci.,29,409–416.(in Chinese)
Rossby,C.-G.,1939:Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action.J.Mar.Res.,2,38–55.
Sardeshmukh,P.D.,and B.J.Hoskins,1988:The generation of global rotational flow by steady idealized tropical divergence.J.Atmos.Sci.,45,1228–1251.
Shi Ning,Shi Danping,and Yan Mingliang,2001:The effects of cross-equatorial current on South China Sea monsoon onset and drought/flood in East China.J. Trop.Meteor.,17,405–414.(in Chinese)
Simmons,A.J.,and B.J.Hoskins,1979:The downstream and upstream development of unstable baroclinic waves.J.Atmos.Sci.,36,1239–1254.
Simmons,A.J.,J.M.Wallace,and G.W.Branstator, 1983:Barotropic wave propagation and instability, and atmospheric teleconnection patterns.J.Atmos. Sci.,40,1363–1392.
Smagorinsky,J.,1953:The dynamical influence of large scale heat sources and sinks on the quasi-stationary mean motions of the atmosphere.Quart.J.Roy. Meteor.Soc.,79,342–366.
Smith,R.B.,1979:The influence of mountains on the atmosphere.Adv.Geophys.,21,87–230.
Sobel,A.H.,and C.S.Bretherton,1999:Development of synoptic-scale disturbances over the summertime tropical Northwest Pacific. J.Atmos. Sci.,56, 3106–3127.
Song Jie and Li Chongyin,2009:The linkages between the Antarctic oscillation and the Northern Hemisphere circulation anomalies. Chinese J.Atmos. Sci.,33,847–858.(in Chinese)
Suo Miaoqing,Ding Yihui,and Wang Zunya,2008:Relationship between Rossby wave propagation in southern branch of westerlies and the formation of the
southern branch trough in wintertime.J.Appl.Meteor.Sci.,19,731–740.(in Chinese)
Takaya,K.,and H.Nakamura,1997:A formulation of a wave-activity flux for stationary Rossby waves on a zonally varying basic flow.Geophys.Res.Lett.,24, 2985–2988.
Takaya,K.,and H.Nakamura,2001:A formulation of a phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow.J.Atmos.Sci.,58,608–627.
Tam,C.-Y.,and T.Li,2006:The origin and dispersion characteristics of the observed tropical summertime synoptic-scale waves over the western Pacific.Mon. Wea.Rev.,134,1630–1646.
Tan Benkui,1990:The stability of Rossby waves in a stratified shear fluid.Acta Meteor.Sinica,46,486–490.(in Chinese)
Tan Benkui,1993:Nonlinear Rossby waves and their interactions.Part II:Periodic wave solution and its stability.Acta Scicentiarum Naturalum Universitis Pekinesis,29,378–384.(in Chinese)
Tan Benkui,2008:Advances of atmospheric Rossby waves dynamics.Acta Meteor.Sinica,66,870–879.(in Chinese)
Tan Benkui and Wen Chen,2014:Progress in the study of the dynamics of extratropical atmospheric teleconnection patterns and their impacts on East Asian climate.J.Meteor.Res.,28,780–802.
Tan,B.K.,J.C.Yuan,Y.Dai,et al.,2015:The linkage between the eastern Pacific teleconnection pattern and convective heating over the tropical western Pacific.J.Climate,28,5783–5794.
Ting,M.F.,and P.D.Sardeshmukh,1993:Factors determining the extratropical response to equatorial diabatic heating anomalies.J.Atmos. Sci.,50, 907–918.
Ting,M.F.,1996:Steady linear response to tropical heating in barotropic and baroclinic models.J.Atmos.Sci.,53,1698–1709.
Ting,M.F.,and L.H.Yu,1998:Steady response to tropical heating in wavy linear and nonlinear baroclinic models.J.Atmos.Sci.,55,3565–3562.
Tokinaga,H.,S.-P.Xie,C.Deser,et al.,2012:Slowdown of the Walker circulation driven by tropical Indo-Pacific warming.Nature,491,439–443.
Tomas,R.A.,and P.J.Webster,1994:Horizontal and vertical structure of cross-equatorial wave propagation.J.Atmos.Sci.,51,1417–1430.
Trenberth,K.E.,1986:An assessment of the impact of transient eddies on the zonal flow during a blocking episode using localized Eliassen-Palm flux diagnostics.J.Atmos.Sci.,43,2070–2087.
Trenberth,K.E.,A.G.Dai,G.van der Schrier,et al., 2014:Global warming and changes in drought.Nat. Climate Change,4,17–22.
Tucker,G.B.,1965:The equatorial tropospheric wind regime.Quart.J.Roy.Meteor.Soc.,91,140–150. Vecchi,G.A.,and B.J.Soden,2007:Global warming and the weakening of the tropical circulation.J. Climate,20,4316–4340.
Wallace,J.M.,and V.E.Kousky,1968:Observational evidence of Kelvin waves in the tropical stratosphere. J.Atmos.Sci.,25,900–907.
Wallace,J.M.,and D.S.Gutzler,1981:Teleconnections in the geopotential height field during the Northern Hemisphere winter.Mon.Wea.Rev.,109,748–812.
Wang,B.,J.Liu J,H.-J.Kime,et al.,2013:Northern Hemisphere summer monsoon intensified by mega-El Ni˜no/southern oscillation and Atlantic multidecadal oscillation.Proc.Natl.Acad.Sci.USA,110, 5347–5352.
Wang,L.,R.H.Huang,L.Gu,et al.,2009:Interdecadal variations of the East Asian winter monsoon and their association with quasi-stationary planetary wave activity.J.Climate,22,4860–4872.
Warn,T.,and H.Warn,1978:The evolution of a nonlinear critical level.Stud.Appl.Math.,59,37–71.
Watterson,I.G.,and E.K.Schneider,1987:The Effect of the Hadley circulation on the meridional propagation of stationary waves.Quart.J.Roy.Meteor. Soc.,113,779–813.
Webster,P.J.,1973:Temporal variation of low-latitude zonal circulations.Mon.Wea.Rev.,101,803–816.
Webster,P.J.,and D.G.Curtin,1975:Interpretations of the EOLE experiment.II:Spatial variation of transient and stationary modes.J.Atmos.Sci.,32, 1848–1863.
Webster,P.J.,and J.R.Holton,1982:Cross-equatorial response to middle-latitude forcing in a zonally varying basic state.J.Atmos.Sci.,39,722–733.
Webster,P.J.,and H.-R.Chang,1988:Equatorial energy accumulation and emanation regions:Impacts of a zonally varying basic state.J.Atmos.Sci.,45, 803–829.
Webster,P.J.,and S.Yang,1989:The three-dimensional structure of perturbation kinetic energy and its relationship to the structure of the zonal wind field. J.Climate,2,1210–1222.
Webster,P.J.,and H.-R.Chang,1998:Atmospheric wave propagation in heterogeneous flow:Basic flow controls on tropical-extratropical interaction and equatorial wave modification.Dyn.Atmos.Oceans, 27,91–134.
Whitham,G.B.,1965:A general approach to linear and non-linear dispersive waves using a Lagrangian.J. Fluid Mech.,22,273–283.
Widlansky,M.J.,P.J.Webster,and C.D.Hoyos,2011: On the location and orientation of the South Pacific convergence zone.Climate Dyn.,36,561–578.
Williams,A.P.,and C.Funk,2011:A westward extension of the warm pool leads to a westward extension of the Walker circulation,drying eastern Africa.Climate Dyn.,37,2417–2435.
Wilson,J.D.,and M.Mak,1984:Tropical response to lateral forcing with a latitudinally and zonally nonuniform basic state.J.Atmos.Sci.,41,1187–1201.
Wu Guoxiong and Chen Biao,1989:Non-acceleration theorem in a primitive equation system.I:Acceleration of zonal mean flow.Adv.Atmos.Sci.,6,1–20.
Yanai,M.,and T.Maruyama,1966:Stratospheric wave disturbances propagating over the equatorial Pacific. J.Meteor.Soc.Japan,44,291–294.
Yanai,M.,T.Maruyama,T.Nitta,et al.,1968:Power spectra of large scale disturbances over the tropical Pacific.J.Meteor.Soc.Japan,46,308–323.
Yeh,T.-C.,1949:On energy dispersion in the atmosphere.J.Meteor.,6,1–16.
Zeng,Q.-C.,1983a:The evolution of a Rossby-wave packet in three-dimensional baroclinic atmosphere. J.Atmos.Sci.,40,73–84.
Zeng,Q.-C.,1983b:The development characteristics of quasi-geostrophic baroclinic disturbances. Tellus, 35A,337–349.
Zeng Qingcun and Li Jianping,2002:Interactions between the Northern and Southern Hemispheric atmospheres and the essence of monsoon.Chinese J. Atmos.Sci.,26,433–448.(in Chinese)
Zhang,C.D.,and P.J.Webster,1989:Effects of zonal flows on equatorially trapped waves.J.Atmos.Sci., 46,3632–3652.
Zheng,J.,Q.Y.Liu,C.Z.Wang,et al.,2013:Impact of heating anomalies associated with rainfall variations over the Indo-western Pacific on Asian atmospheric circulation in winter.Climate Dyn.,40,2023–2033.
Zhou Putian,Suo Lingling,Yuan Jiacan,et al.,2012:The East Pacific wavetrain:Its variability and impact on the atmospheric circulation in the boreal winter. Adv.Atmos.Sci.,29,471–483.
:Yang Song,Deng Kaiqiang,Ting Mingfang,et al.,2015:Advances in research on atmospheric energy propagation and the interactions between different latitudes.J.Meteor.Res.,29(6), 859–883,
10.1007/s13351-015-5088-5.
Supported by the National(Key)Basic Research and Development(973)Program of China(2014CB953900),National Natural Science Foundation of China(41375081),LASW State Key Laboratory Special Fund(2013LASW-A05),and China Meteorological Administration Special Public Welfare Research Fund(GYHY201406018).
∗Corresponding author:dengkq@mail2.sysu.edu.cn.
©The Chinese Meteorological Society and Springer-Verlag Berlin Heidelberg 2015
(Received May 1,2015;in final form September 14,2015)
杂志排行
Journal of Meteorological Research的其它文章
- Impact of Updraft on Neutralized Charge Rate by Lightning in Thunderstorms:A Simulation Case Study
- Development and Testing of the GRAPES Regional Ensemble-3DVAR Hybrid Data Assimilation System
- Role of a Meso-γ Vortex in Meiyu Torrential Rainfall over the Hangzhou Bay,China:An Observational Study
- Effect of Urbanization on the Urban Meteorology and Air Pollution in Hangzhou
- Seasonal Inhomogeneity of Soot Particles over the Central Indo-Gangetic Plains,India:Influence of Meteorology
- ENSO-Independent Contemporaneous Variations of Anomalous Circulations in the Northern and Southern Hemispheres:The Polar-Tropical Seesaw Mode
