A High-order Coupled Compact Integrated RBF Approximation Based Domain Decomposition Algorithm for Second-order Differential Problems

C.M.T.Tien,N.Pham-Sy,N.Mai-Duy,C.-D.Tranand T.Tran-Cong

A High-order Coupled Compact Integrated RBF Approximation Based Domain Decomposition Algorithm for Second-order Differential Problems

C.M.T.Tien1,N.Pham-Sy1,N.Mai-Duy1,C.-D.Tran1and T.Tran-Cong1

This paper presents a high-order coupled compact integrated RBF(CC IRBF)approximation based domain decomposition(DD)algorithm for the discretisation of second-order differential problems.Several Schwarz DD algorithms,including one-level additive/multiplicative and two-level additive/multiplicative/hybrid,are employed.The CCIRBF based DD algorithms are analysed with different mesh sizes,numbers of subdomains and overlap sizes for Poisson problems.Our convergence analysis shows that the CCIRBF two-level multiplicative version is the most effective algorithm among various schemes employed here.Especially,the present CCIRBF two-level method converges quite rapidly even when the domain is divided into many subdomains,which shows great promise for either serial or parallel computing.For practical tests,we then incorporate the CCIRBF into serial and parallel two-level multiplicative Schwarz.Several numerical examples,including those governed by Poisson and Navier-Stokes equations are analysed to demonstrate the accuracy and efficiency of the serial and parallel algorithms implemented with the CCIRBF.Numerical results show:(i)the CCIRBF-Serial and-Parallel algorithms have the capability to reach almost the same solution accuracy level of the CCIRBF-Single domain,which is ideal in terms of computational calculations;(ii)the CCIRBF-Serial and-Parallel algorithms are highly accurate in comparison with standard finite difference,compact finite difference and some other schemes;(iii)the proposed CCIRBF-Serial and-Parallel algorithms may be used as alternatives to solve large-size problems which the CCIRBF-Single domain may not be able to deal with.The ability of producing stable and highly accurate results of the proposed serial and parallel schemes is believed to be the contribution of the coarse mesh of the two-level domain decomposition and the CCIRBF approximation.It is noted that the focus of this paper is on the derivation of highly accurate serial and parallel algorithms for second-order differential problems.The scope of this work does not cover a thorough analysis of computational time.

Coupled compact integrated RBF(CCIRBF),Schwarz,domain decomposition,one-level,two-level,coarse meshes,additive,multiplicative,hybrid,serial,parallel,colouring technique,Poisson equation,Naiver-Stokes equation,lid driven cavity.

1 Introduction

Traditional techniques such as the finite difference method(FDM), finite volume method(FVM), finite element method(FEM)and boundary element method(BEM)are among the most popular numerical solution methods for partial differential equations(PDEs)governing many problems in engineering and sciences.These methods are based on some discretisation of a problem domain into small elements.These elements are not overlapping each other.If an element is heavily distorted,approximations on this element are of poor quality,leading to unacceptable accuracy or possibly failed computation.Element-free methods are developed to address the issues associated with element distortions by using different approximation methods over a cluster of scattered nodes.The smooth particle hydrodynamics method(SPH)[Lucy(1977)]is one of the initial and well developed elementfree methods.The diffusive element method(DEM)[Nayroles,Touzot,and Villon(1992)]was the first element-free method to employ moving least squares(MLS)approximation[Lancaster and Salkauskas(1981)]in constructing their shape functions over scattered nodes.Several element-free methods have been proposed since then,including the element-free Galerkin method(EFG)[Belytschko,Lu,and Gu(1994)],reproducing kernel particle method(RKPM)[Liu,Chen,Chang,and Belytschko(1996)],partition of unity(PU)method[Babuska and Melenk(1997)]and meshless local Petrov-Galerkin method(MLPG)[Atluri and Zhu(1998)].For an overview on these element-free methods,readers may find more details in[Belytschko,Krongauz,Organ,Fleming,and Krysl(1996);Chen,Lee,and Eskandarian(2006)]and references therein.

In the last three decades,there has been great interest in using element-free radial basis function(RBF)methods for the numerical solutions of various types of PDEs.Kansa(1990a,b)introduced a new approach for this kind of problems,using radial basis functions(RBFs)(here referred as differential/direct RBF or DRBF)for the approximate solutions of PDEs.Mai-Duy and Tran-Cong(2001a,b,2003)then proposed an idea of using indirect/integrated radial basis functions(IRBFs)for the solution of PDEs.Numerical examples in Mai-Duy and Tran-Cong(2001a,b,2003,2005)show that the IRBF approach achieves a greater accuracy than the DRBF approach.It has been shown that these RBF methods are more accurate than the traditional techniques such as the FDM,FVM and FEM[Zerroukat,Power,and Chen(1998);Li,Cheng,and Chen(2003);Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2012)].Furthermore,the RBF approaches can work with simple discretisation based on a Cartesian grid.However,when dealing with large-scale problems,a big obstacle for the global RBF method is that the system matrix is generally illconditioned,non-symmetric and dense.Therefore,the RBF method needs to be combined with the domain decomposition(DD)method to reduce the density and ill-conditioning of the matrix for an accurate solution.

The earliest idea of DD was introduced as a classical Schwarz alternating algorithm by Schwarz in 1870.Generally,DD methods can be classified into two major methods:overlapping methods,which are referred to as Schwarz methods,and non-overlapping methods,which are referred to as iterative substructuring or Schur complement methods[Smith,Bjorstad,and Gropp(1996);Quarteroni and Valli(1999);Toselli and Widlund(2005)].In this work,we will concentrate on iterative Schwarz DD methods using overlapping subdomains.The overlapping DD methods have a simple algorithmic structure because there is no need to solve the continuity problem across subdomain interfaces[Cai(2003)].The overlapping methods provide parallel,potentially fast and robust algorithms for the solution of linear or nonlinear systems of equations resulting usually from the discretisation of PDEs.It is noted that the convergence characteristics of the DD based methods are sensitive to the choice of the number of subdomains,mesh sizes and overlap sizes.In particular,having too many subdomains leads to a very large coarse mesh problem,while having too few subdomains requires the solution of large problems for each subdomain.Furthermore,having too small overlaps usually leads to large number of iterations,while having too large overlaps leads to the solution of large problems for each subdomain.In this point of view,efficient DD based methods should stably converge with small number of iterations for a wide range of numbers of subdomains and mesh sizes,using small number of overlaps.

In this paper,we investigate convergence characteristics of the recently developed three-point coupled compact integrated RBF(CCIRBF)approximation schemepro posed in[Tien,Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2015)]when incorporated into the Schwarz DD algorithms for solving Poisson problems.Different types of Schwarz DD algorithms are utilised,including the one-level additive/multiplicative and two-level additive/multiplicative/hybrid Schwarz.In the one-level algorithm,a fine mesh problem on each subdomain is solved and the subdomain solutions are interpolated back to the global grid.The two-level algorithm is formulated by adding the coarse mesh problem to the one-level problem.The use of the coarse mesh generally reduces the number of iterations.The present CCIRBF based Schwarz DD algorithms are investigated with various grid sizes,number of subdomains and overlap sizes.It is found that the present CCIRBF two-level multiplicative version is far better than the other CCIRBF based DD versions in terms of iteration count.The present CCIRBF two-level multiplicative version shows a great promise for both serial and parallel computing because it is stable with various numbers of subdomains and grid sizes while being able to converge quickly with very small overlap sizes.

Then,we incorporate the CCIRBF into serial and parallel two-level multiplicative Schwarz for practical tests.We parallelise problems which are decomposed by the two-level multiplicative Schwarz with a colouring technique.The serial and parallel algorithm are so called CCIRBF-Serial and-Parallel,respectively.To analyse their accuracy and efficiency,analytical examples including Poisson and Navier-Stokes equations are performed.Lid driven cavity problems,in which Taylor-series type boundary condition for vorticity is first implemented in the context of the CCIRBF,are also analysed as practical applications.Numerical results show:(i)the results produced by CCIRBF-Serial and-Parallel have almost the same solution accuracy with those calculated by the CCIRBF-Single domain,which is computationally ideal;(ii)the CCIRBF-Serial and-Parallel algorithms are highly accurate in comparison with standard FDM,higher-order compact finite difference(HOC)and some other schemes;(iii)the proposed CCIRBF-Serial and-Parallel algorithms can efficiently solve large-size problems.The proposed CCIRBF-Serial and Parallel algorithms may be used effectively for large-scale problems which the single domain algorithms are struggling to handle.

This paper is organised as follows.Section 2 reviews the CCIRBF approximation scheme.In Section 3,we briefly describe the one-level additive/multiplicative and two-level additive/multiplicative/hybrid.In Section 4,the GMRES iterative method is briefly mentioned.Section 5 explains the serial and parallel two-level multiplicative Schwarz DD methods,followed by Section 6 which details the parallel technique.Numerical examples demonstrating the convergence analysis and effectiveness of the algorithms are presented in Section 8.Finally,the concluding remarks of the article are given in Section 9.

2CCIRBF scheme

The coupled compact integrated radial basis function(CCIRBF)approximation scheme developed by Tien,Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2015)is utilised in this paper.Readers may find more details about CCIRBF scheme in[Tien,Thai-Quang,Mai-Duy,Tran,and Tran-Cong(2015)],which are summarised here for convenience.

The essence of the CCIRBF scheme is to couple extra information of the nodal first and second derivative values via their identity equations,which makes the scheme more accurate,stable and efficient.Hereafter,for brevity,η denotes either x or y in a generic local stencil{η1,η2,η3},where η1＜ η2＜ η3and η2≡ η(i,j),are illustrated in Figure 1.

Figure 1:Compact three-point 1D-IRBF stencil for interior nodes.

2.1 First derivatives at interior nodes

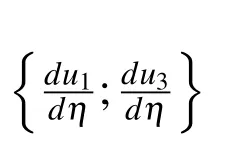
At η = η2,the approximation formulation of the stencil is expressed in the matrixvector form as

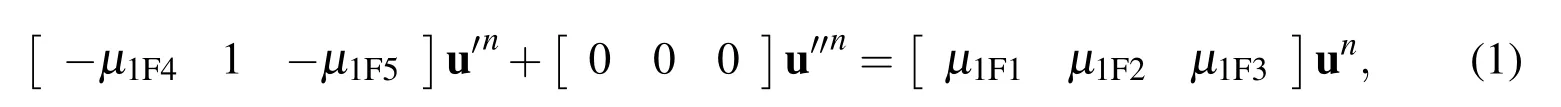
At η = η2,the approximation formulation of the stencil is expressed in the matrixvector form as

2.1.3 First derivative couplings at interior nodes

At η = η2,a coupling equation in matrix-vector form is described as

2.2 First derivatives at boundary nodes

At the boundary nodes,the first derivatives are approximated in special compact stencils.Consider the boundary node,e.g.η1.Its associated stencil is{η1,η2,η3,η4}as shown in Figure 2.For the coupled compact approximation of the first derivative at the boundary node η1,nodal derivative values(i.e.extra information)are chosen as bothandThe approximation is processed through three steps:(i)we first approximate its first derivative over its associated four-point stencil involving(ii)we then approximate its first derivative over the same stencil used in step(i)involving(iii)an identity equation of the second derivative is employed to enhance the level of compactness of the stencil.Bothandare incorporated into the second derivative approximation.

Figure 2:Special compact four-point 1D-IRBF stencil for boundary nodes.

2.2.1 First derivatives at boundary node η1involving

where

2.2.2 First derivatives at boundary node η1involving

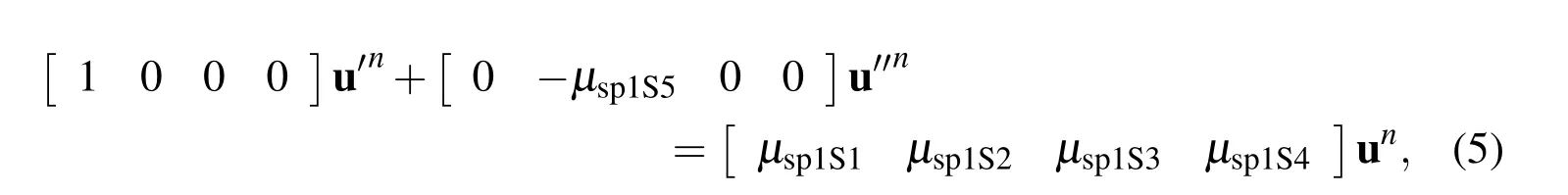
where

2.2.3 First derivative coupling at boundary node η1

whereand

In a similar manner,one is able to calculate the first derivative at the boundary node

2.3 Second derivatives at interior nodes

In a similar manner as in Section 2.1,one is able to calculate the coupled compact approximation of the second derivatives at interior nodes as follows.

At η = η2,the approximation formulation of the stencil is expressed in the matrixvector form as

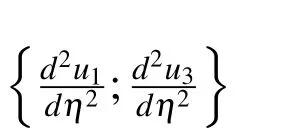
At η = η2,the approximation formulation of the stencil is expressed in the matrixvector form as

2.3.3 Second derivative couplings at interior nodes

At η = η2,a coupling equation in the matrix-vector form is described as

2.4 Second derivatives at boundary nodes

In a similar manner as in Section 2.2,one is able to calculate the coupled compact approximation of the second derivatives at boundary nodes as follows.

2.4.1 Second derivatives at boundary node η1involving

whereand

2.4.2 Second derivatives at boundary node η1involving

whereand

2.4.3 Second derivative coupling at boundary node η1

whereand

In an similar manner,one is able to calculate the second derivative at the boundary node ηnη.

2.5 Matrix assembly for first and second derivative expressions

The IRBF system on a grid line for the first derivative is obtained by letting the interior node taking value from 2 to(nη−1)in(1),(2),and(3);and,making use of(4),(5),and(6)for the boundary nodes 1 and nη.In a similar manner,the IRBF system on a grid line for the second derivative is obtained by letting the interior node taking value from 2 to(nη−1)in(7),(8),and(9);and,making use of(10),(11),and(12)for the boundary nodes 1 and nη.The resultant matrix assembly is expressed as

whereDηandDηηare nη×nηmatrices.The approximations of the first and second derivatives,u′andu′′,respectively,are will be used in the following sections.

3 Domain decomposition preconditioners

This paper presents the implementation of the Schwarz domain decomposition(DD)preconditioned GMRES techniques using the CCIRBF approximation scheme for the convergence analysis for Poisson problems.In order to describe the working principles of the Schwarz DD methods,we will first reintroduce the classical alternating and parallel Schwarz algorithms for Poisson problems as below.For more information about the Schwarz DD methods,readers are referred to the literature in[Smith,Bjorstad,and Gropp(1996);Danaila(2007)].

3.1 Classical Schwarz

In one dimension,the Poisson problem is expressed as follows.

where u′′are the operators of the approximation of the second derivative;f are given right hand side values;u are solutions;and uaand ubare boundary values.The computational interval[a,b]is discretised on n+2 points xi=a+ih for i=0,...,n+1 with a uniform stepFor simplicity,we decompose the computational interval[a,b]into two subintervals with overlapping:we choose odd value n and two integer values iland irsymmetric with respect tosuch thatWe set xl=ilh and xr=irh,thus defining two intervals[a,xr]and[xl,b]with a nonempty overlapThe problem domain and subdomains becomeandrespectively.It is noted that the domains Ω,Ω1and Ω2do not include their boundaries and

We now compute the solution u to the problem(16)by solving two problems on subintervals[a,xr]and[xl,b].The solution u1(respectively u2)is expected to be the restriction on the[a,xr](respectivelyof the solution u to the problem on the full interval[a,b].The two solutions u1and u2must therefore be identical within the overlapping region,which allows us to define the boundary conditions in xland xr

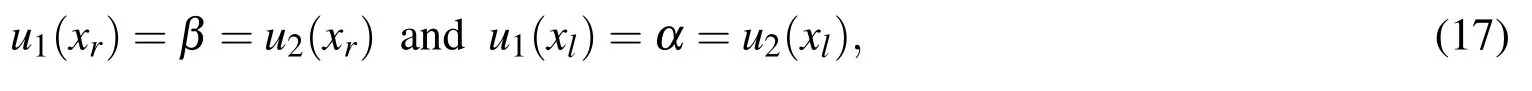
Initially,the values of α and β are"guessed"by linear interpolation of the global boundary conditions

3.1.1 Classical Alternating Schwarz

In alternating Schwarz method,a sequencefor n≥0 is built by solving alternatively the same equations(16)in[a,xr]and[xl,b]with the values on the boundary defined by the previously computed values in the other subdomain.The alternating Schwarz method begins by selecting an initial guessThen,iteratively for n=1,2,3...,one solves the boundary value problem

3.1.2 Classical Parallel Schwarz

In parallel Schwarz method,we setand.The computations in[a,xr]and[xl,b]are made in parallel

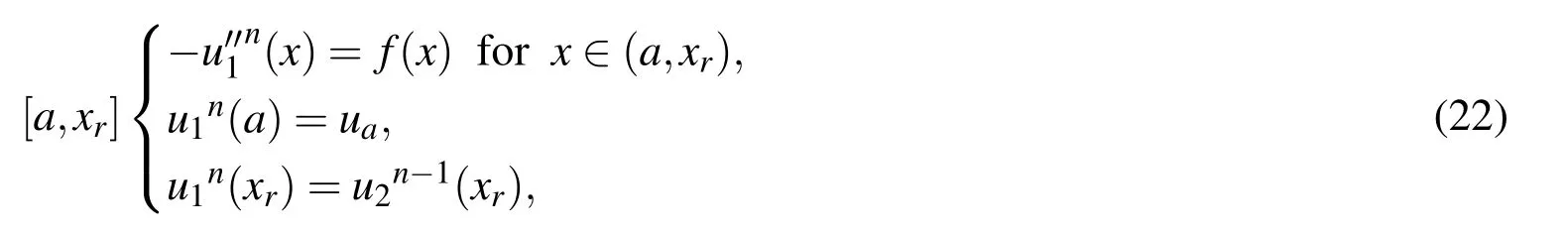
and

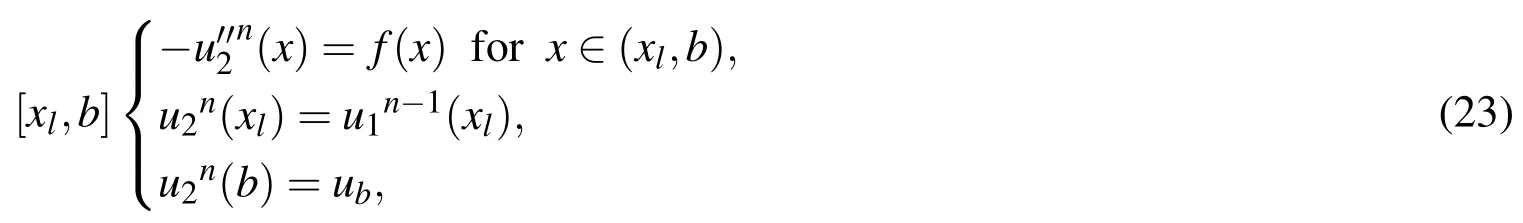
The classical algorithms described above can be modified to get additive,multiplicative and hybrid DD preconditioners used in a Krylov subspace solver such as GMRES.For convenience,we only summarise those DD preconditioners in this paper as below.For more details,readers refer to[Smith,Bjorstad,and Gropp(1996)]).

3.2 Addictive,multiplicative and hybrid Schwarz preconditioner

Figure 3 illustrates the decomposition of the global domain Ω into two subdomains Ωi,where Ωiare overlapping subdomains.We define the restriction mapRifrom global domain Ω to subdomain Ωias follows.

Figure 3:An example of decomposition of a domain into two subdomains.

whereIare identity matrices.Then,subdomain matrix is defined as

whereAis the problem system matrix andis the interpolation map from global domain Ω to subdomain Ωi.For general description,we assume that the global domain Ω is divided into q-subdomains,where q≥2.

3.2.1 One-level additive Schwarz preconditioner

The one-level additive Schwarz preconditioner is simply formulated as

Algorithm 1:one-level additive Schwarz preconditioner

whereris the residual;restricts the residualrto subdomain Ωi;andvis Krylov vector in the GMRES algorithm.

3.2.2 One-level multiplicative Schwarz preconditioner

One-level multiplicative Schwarz preconditioner,the sequential version of the onelevel additive Schwarz preconditioner,is expressed as follows.

Algorithm 2:one-level multiplicative Schwarz preconditioner

Figure 4:An example of discretisation of two coarse meshes.

Partition of unity coarse meshes for two-level algorithms:In the two-level methods,coarse meshes need to be constructed.We de fine the coarse mesh on the existing fine mesh[Jenkins,Kees,Kelley,and Miller(2001)].By this way,we do not need to create the coarse mesh geometry or use the geometric information about subdomains.Figure 4 shows the discretisation of a fine mesh into two coarse meshes with one coarse mesh map per subdomain Ωi,whereis an overlapping region.We use a partition of unity(PU),i.e.to sum up to one everywhere in the domain of calculation.We letPibe a PU subordinate to the covering partition Ωiof Ω with the following conditions

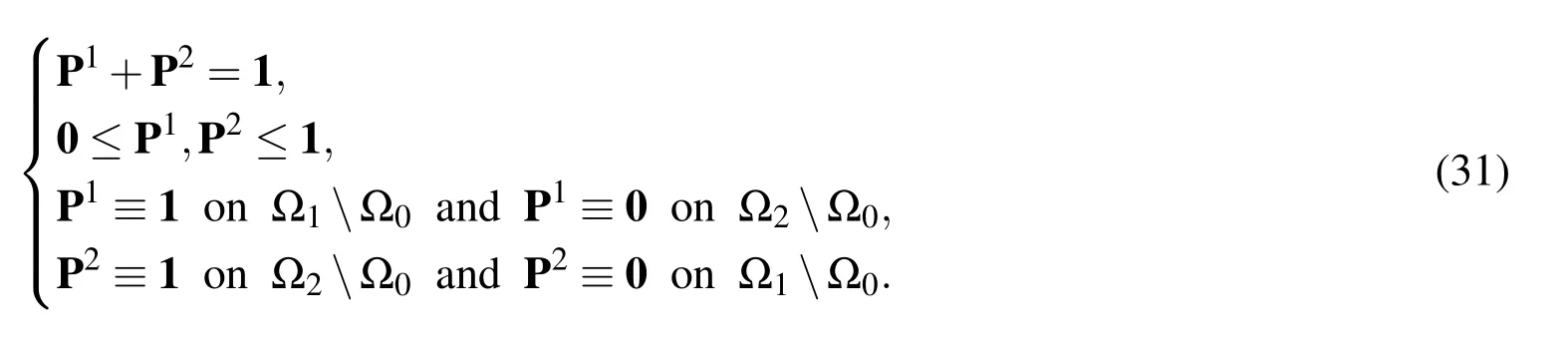
Similarly to the one-level,we will chooseR0,a coarse mesh restriction map from fine to coarse meshes,such that it has the form

whereW1andW2are de fined as

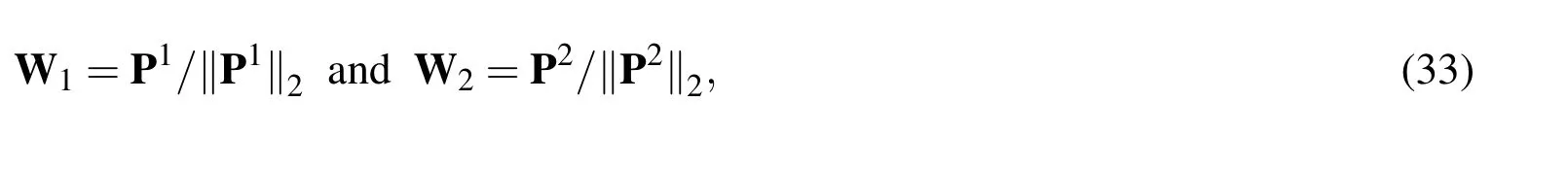
whereis a coarse mesh interpolation map from fine to coarse meshes.For general description,we again assume that the global domain Ω is divided into qsubdomains,where q≥2.

3.2.3 Two-level additive Schwarz preconditioner

The two-level additive Schwarz is formed by adding the coarse mesh problem to the one-level additive problem

Algorithm 3:two-level additive Schwarz preconditioner

3.2.4 Two-level multiplicative Schwarz preconditioner

The two-level multiplicative Schwarz is formed by adding the coarse mesh problem to the one-level multiplicative as follows.It is noted that the coarse mesh problem is solved only once at the beginning of calculation.

Algorithm 4:two-level multiplicative Schwarz preconditioner

3.2.5 Two-level hybrid I Schwarz preconditioner

The two-level hybrid I is formulated on the basis of the one-level multiplicative by adding the coarse mesh problem to its last stage

Algorithm 5:two-level hybrid I Schwarz preconditioner

3.2.6 Two-level hybrid II Schwarz preconditioner

The two-level hybrid II is formulated on the basis of the one-level additive by adding the coarse mesh problem to its last stage

Algorithm 6:two-level hybrid II Schwarz preconditioner

4 GMRES

We utilise a generalised minimal residual algorithm(GMRES)for solving non symmetric linear systems.More information about GMRES may be found in[Saad and Schultz(1986);Behr(2014);Strang(2007)].Consider the linear system

wherefare given right hand side values;uare unknowns;andAis the problem system matrix.The GMRES algorithm is outlined in Table 1,where Algorithm★is used to represent one of the six preconditioning algorithms mentioned above and ε is the GMRES tolerance.

5 Serial and parallel two-level multiplicative Schwarz DD methods

For numerical examples,we incorporate the CCIRBF into serial and parallel twolevel multiplicative Schwarz DD methods to solve the linear system(45)as follows.

5.1 Serial two-level multiplicative Schwarz

First,solve the coarse mesh problem once at the beginning

Then,solve the fine mesh problem

where

Table 1:GMRES Algorithm.

5.2 Parallel two-level multiplicative Schwarz

The serial two-level multiplicative Schwarz method mentioned above has very little potential for parallelism.This is easily fixed.It is noted that there are often many subdomains which share no common grid points as shown in Figure 5.The numerical solution on these subdomains,therefore,could be updated simultaneously,in parallel.

Figure 5:Colouring of 5×5 subdomains into four classes.

De fine a colouring of the subdomains in the way described in[Smith,Bjorstad,and Gropp(1996)].For each subdomain,we associate a colour in the way that no two subdomains sharing common grid points have the same colour.Let i be the number of colours used.

In this paper,we introduce the coarse mesh problem into the original colouring technique of Smith,Bjorstad,and Gropp(1996).We can now generate a i-step method as follows.

First,solve the coarse mesh problem once at the beginning

Then,solve the fine mesh problem

where(n+1)is the current time level.

6 Parallelism

The parallel implementation is based on the colouring technique explained in Section 5.2.As shown in Figure 5,four colours are used to mark colours of subdomains so that subdomains with the same colour do not overlap each other.In each sub-step from(50)to(52),one colour is considered,each CPU is assigned to solve the problem in each subdomain within that colour.Then,the result from subdomains will be exchanged between themselves in order for each subdomain to obtain a unique copy of the whole domain solution.In next substep,the next colour is considered until the convergence measurement reaches a predefined value.

In this implementation,the broadcast communication is used because each subdomain needs to send information to and receive it from all other subdomains.As whole domain solution is kept in each subdomain and is updated after each substep,the convergence measurement calculated in each subdomain is consistent with all other subdomains.This ensures the concurrent convergence of subdomains and thus alleviate the need of a dedicated termination algorithm for the whole system.

7 Stream function-vorticity formulation

The transient Navier-Stokes equations for an incompressible viscous fluid in the stream function-vorticity formulation are expressed in the dimensionless conservative forms as follows.

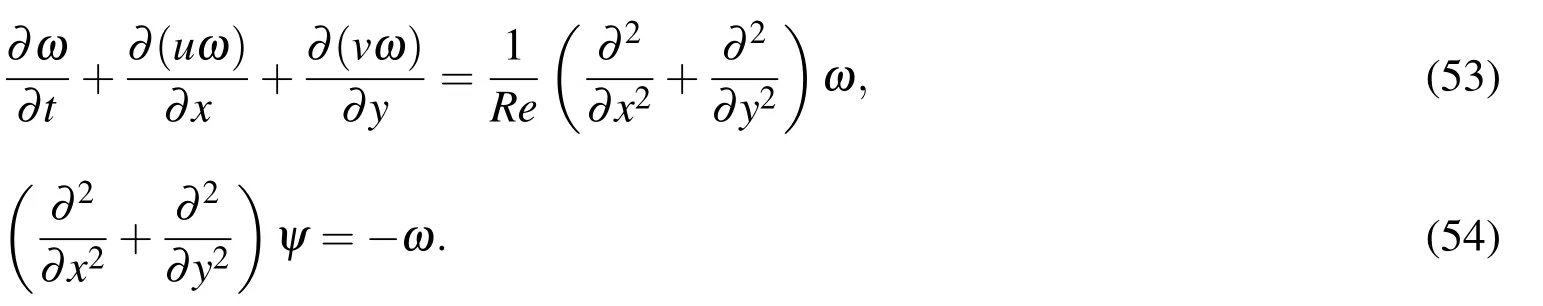
It is well known that equations in conservative form generally produce more accurate results compared to those of non-conservative form[Niyogi,Chakrabartty,and Laha(2009)].In equations(53)and(54),ψ is the stream function;ω is the vorticity;Re=Ul/ν is the Reynolds number,in which ν,l and U are the kinematic viscosity,characteristic length and characteristic speed of the flow,respectively;u and v,velocity components in x-and y-direction,are given by

At current time level,n,stream function equation is expressed as

And velocities are expressed as

The temporal discretisation of(53)results in

8 Numerical examples

We chose the MQ function as the basis function in the present calculations

where ciand aiare the centre and the width of the i-th MQ,respectively.For each stencil,the set of nodal points is taken to be the same as the set of MQ centres.We simply choose the MQ width as ai= βhi,where β is a positive scalar and hiis the distance between the i-th node and its closest neighbour.

Measurement Criteria:We evaluate the performance of the present schemes through the following measures

i.the root mean square error(RMS)is defined as

where fiandare the computed and exact values of the solution f at the i-th node,respectively;and,N is the number of nodes over the whole domain.

ii.the average absolute error(L1)is defined as

iii.the global convergence rate with respect to the grid refinement is defined through

where h is the grid size;and γ and α are exponential model’s parameters.

iv.a flow is considered to reach its steady state when

v.Speed-up,S,and efficiency,E are defined as

where Tsis computation time on single CPU;Tpis computation time on parallel CPUs;and p is number of parallel CPUs.In particular,Tsis defined as the computation time of the CCIRBF-Single domain in this paper.

Subdomain partition:Referring the subdomain partition presented in[Jenkins,Kees,Kelley,and Miller(2001)],we let h=2−mbe the scale of the fine mesh and let the overlap o be the nearest integer larger than

where o1is the overlap that depends on the physical subdomain.For examples,overlap of 1%is determined by letting o1=0.01.The global grid is an n×n mesh where n=2m+o.We will use 2psubdivisions in each directions so there will be 2p+1subdomains,each of size m×m,where

The scale H of the subdomains is defined as 2−p.This way of partition allows for a perfect split with all intervals having equal length.Figure 6 illustrates an example of decomposition of the 2D domain Ω.

In this work,calculations are done with a Dell computer,Precision T7600.Its specifications are Intel(R)Xeon(R)CPU E5-2687W 0 3.10 GHz 3.10 GHz(2 processors),memory(RAM)of 128GB and 64-bit operating system.The Matlab(R)version 2012 is utilised.In serial and parallel algorithms,the overlapping is chosen between 1%to 25%.In parallel computing,the percentage of communication time is calculated with respect to its total computation time.

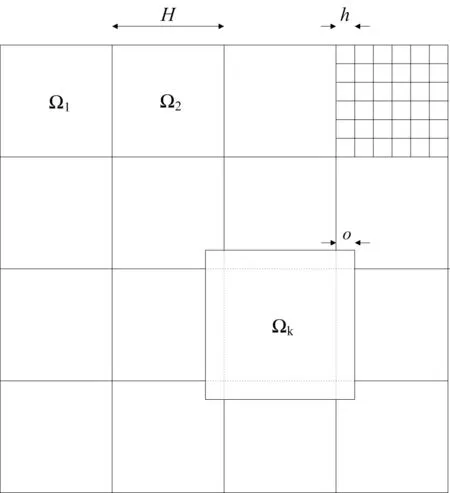
Figure 6:An example of decomposition of Ω into subdomains Ω1,Ω2,...,Ωk,....

8.1 Convergence analysis of CCIRBF based additive/multiplicative/hybrid Schwarz for 2D Poisson

We now apply the GMRES algorithms described in Section 4 for the 2D case.The 2D Poisson problem becomesWe consider the right hand side f equal to −2π2sin(πx)sin(πy)and the solution is required to be zero on the boundary of[0,1]2.Calculations are carried out on coarse meshes of size H=1/4,1/8 and 1/16 and fine meshes of size roughly h=1/32,1/64 and 1/128.The value of β=50 is simply chosen.We terminate calculations when the GMRES residual is smaller than 0.01.We tabulate iteration counts upon termination.In Tables 2-7,H is decreased by a factor of two going down the columns and h is similarly decreased going across the rows.We increase the overlap size as{1%,5%,10%,15%,20%,25%}.We consider calculations having the number of iteration larger than 100 to be not stable and unlikely to converge.For plots of iteration count versus overlap percentage and of GMRES residual versus iteration count,we deliberately choose the case where H=1/8 and h=1/128 to be a representative case for each overlap case because calculations with H=1/8 and h=1/128 are reasonably stable in our experiments.

8.1.1 One-level additive Schwarz preconditioner

Table 2 shows the iteration counts of the one-level additive preconditioned GMRES using the present CCIRBF.More details about convergence characteristics of the present CCIRBF one-level additive algorithm are shown in Figure 7.It appears that the present CCIRBF one-level additive algorithm performs best with an overlap around 20%.

Figure 7:One-level additive preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

Table 2:One-level additive preconditioned GMRES using the present CCIRBF:number of iteration required to achieve convergence.

8.1.2 One-level multiplicative Schwarz preconditioner

The iteration counts of the one-level multiplicative preconditioned GMRES using the present CCIRBF are provided in Table 3.The iteration counts of the present CCIRBF one-level multiplicative algorithm are much smaller than those of the present CCIRBF one-level additive algorithm tabulated in Tables 2,except the case of 1%overlap.Especially,with cases where H=1/16,the iteration counts of the present CCIRBF one-level multiplicative algorithm are much smaller than those figures of the present CCIRBF one-level additive algorithm in Tables 2.Plots of iteration count versus overlap percentage and GMRES residual versus iteration count are illustrated in Figure 8.It can be seen that the present CCIRBF one-level multiplicative algorithm performs best with the overlap between 15%and 20%.

Figure 8:One-level multiplicative preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

Table 3:One-level multiplicative preconditioned GMRES using the present CCIRBF:number of iteration required to achieve convergence.

8.1.3 Two-level additive Schwarz preconditioner

Table 4 shows the iteration counts of the two-level additive preconditioned GMRES using the present CCIRBF.The present CCIRBF two-level additive scheme is comparable with the present CCIRBF one-level additive scheme shown in Table 2.As shown in Figure 9,the present CCIRBF two-level additive scheme performs best with an overlap of around 10%.

8.1.4 Two-level multiplicative Schwarz preconditioner

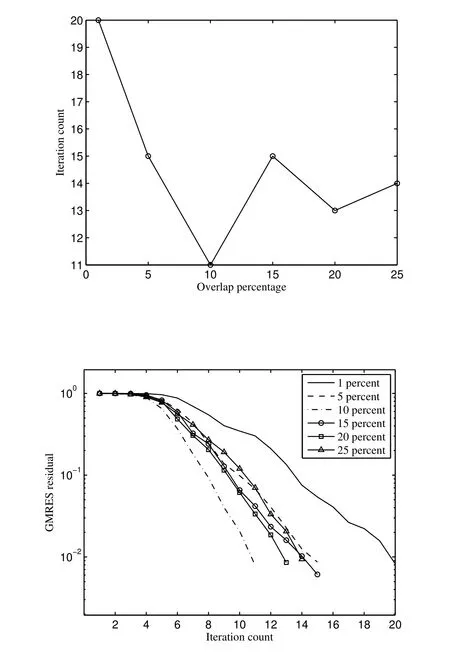
Figure 9:Two-level additive preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

Table 4:Two-level additive preconditioned GMRES using the present CCIRBF:number of iteration required to achieve convergence.

Table 5 shows the iteration statistics of the two-level multiplicative preconditioned GMRES using the present CCIRBF.In comparison with the present CCIRBF onelevel additive/multiplicative and two-level additive algorithms shown in Table 2,3 and 4,respectively,the present CCIRBF two-level multiplicative algorithm is superior with much smaller iterations.Figure 10 depicts fast convergence of the present CCIRBF two-level multiplicative algorithm for overlap from 10%up to 25%.Moreover,the smaller the overlap size,the faster the calculation,and therefore,the overlap of 10%is recommended for the present CCIRBF two-level multiplicative.

For comparison purposes,we incorporate the high order compact finite difference(HOC)of[Tian,Liang,and Yu(2011)]into the DD two-level multiplicative Schwarz preconditioned GMRES algorithm.It can be seen that the present CCIRBF two-level multiplicative scheme produces much better results than those of the HOC two-level multiplicative scheme at the overlap of 1%and 25%.For other overlap cases,the present CCIRBF two-level multiplicative algorithm is com-parable with the HOC two-level multiplicative algorithm.

Figure 10:Two-level multiplicative preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

Table 5:Two-level multiplicative preconditioned GMRES using the HOC and present CCIRBF:number of iteration required to achieve convergence.

8.1.5 Two-level hybrid I Schwarz preconditioner

The iteration statistics of the two-level hybrid I preconditioned GMRES using the present CCIRBF are presented in Table 6.In comparison with the present CCIRBF two-level multiplicative shown in Table 5,the present CCIRBF two-level hybrid I is less effective with larger iteration counts.Plots of iteration count versus overlap percent and GMRES residual versus iteration count for the present CCIRBF twolevel hybrid I are depicted in Figure 11.It can be seen that the present CCIRBF two-level hybrid I performs best around an overlap of 10%.

Figure 11:Two-level hybrid I preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

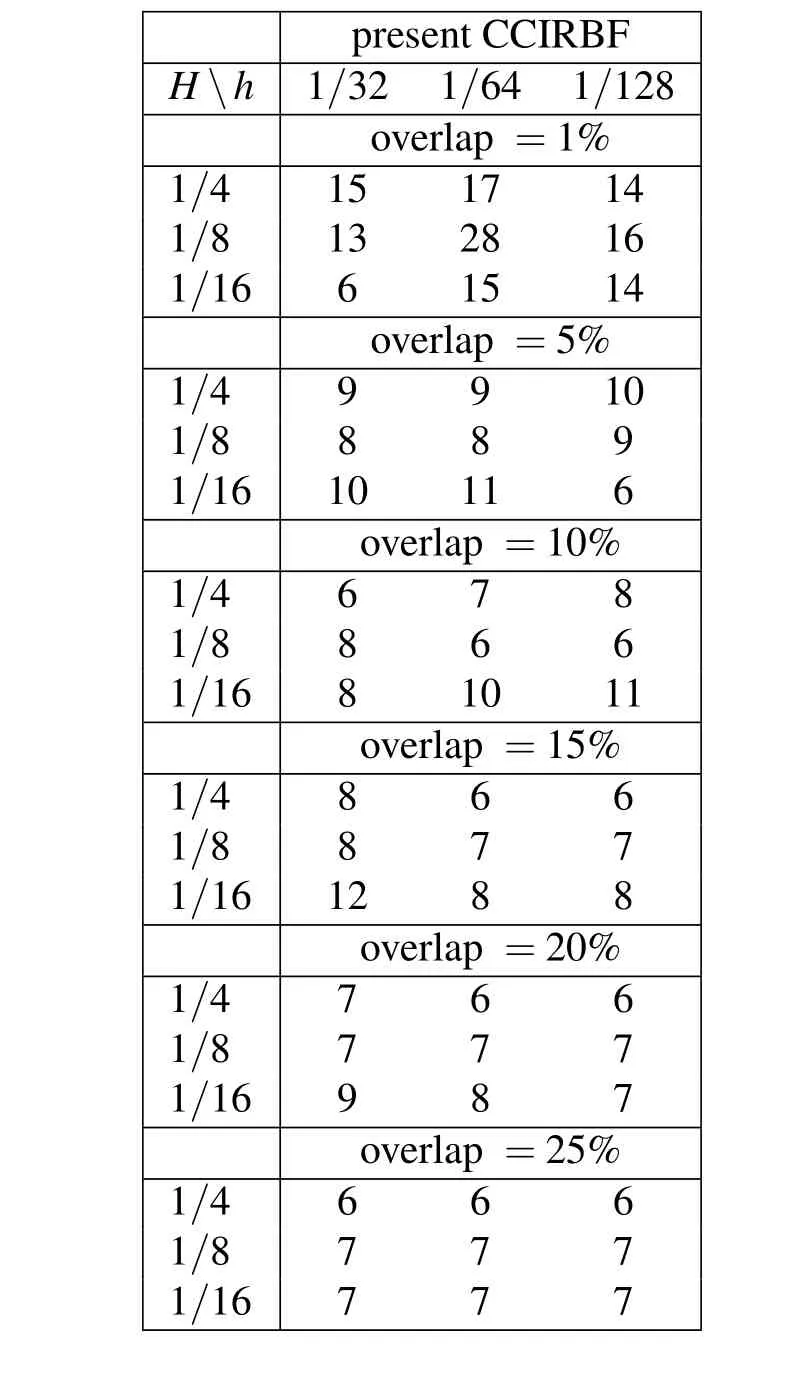
Table 6:Two-level hybrid-I preconditioned GMRES using the present CCIRBF:number of iteration required to achieve convergence.

8.1.6 Two-level hybrid II Schwarz preconditioner

Table 7 reports the iteration counts of the two-level hybrid-II preconditioned GMRES using the present CCIRBF.At the overlap of 1%,5%,10%and 15%,the present CCIRBF two-level hybrid-II shows better results compared to those of the present CCIRBF one-and two-level additive in Tables 2 and 4,respectively.For other overlap cases where H=1/16,the iteration counts of the present CCIRBF two-level hybrid-II algorithm are much smaller than those figures of the present CCIRBF one-and two-level additive algorithm in Tables 2 and 4,respectively.Figure 12 plots the iteration count versus the overlap percent and the GMRES residual versus the iteration count from which it can be observed that the present CCIRBF two-level hybrid-II performs best around an overlap of 10%.

Figure 12:Two-level hybrid II preconditioned GMRES using the present CCIRBF:Iteration count versus overlap percentage(top)and GMRES residual versus iteration count(bottom).

Table 7:Two-level hybrid-II preconditioned GMRES using the present CCIRBF:number of iteration required to achieve convergence.

8.1.7 Final comparison of the six algorithms using the present CCIRBF

For comparison purpose,at H=1/8 and h=1/128,we finally choose the overlap percentages at which each of the six algorithms using the present CCIRBF gives its best performance.Figure 13 shows the comparison of the six algorithms in terms of the GMRES residual versus the iteration count.It can be seen that the present CCIRBF two-level multiplicative at 10%overlap reaches the prescribed residual with the least iterations of only 4.After that,both the present CCIRBF one-level multiplicative at 20%overlap and the present CCIRBF two-level hybrid I at 10%overlap require 6 iterations to reach the prescribed GMRES residual.Then,both the present CCIRBF two-level additive at 10%overlap and the present CCIRBF two-level hybrid II at 10%overlap take 11 iterations to get to the target GMRES residual.

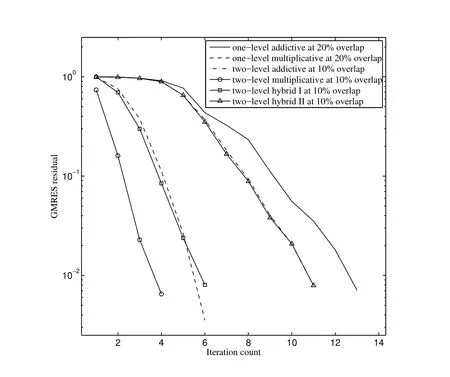
Figure 13:Comparison of the six algorithms using the present CCIRBF:GMRES residual versus iteration count.

8.2 Poisson equation

In order to study the spatial accuracy of the present CCIRBF-Serial and-Parallel algorithms,we consider the following Poisson equation

subject to Dirichlet boundary condition derived from the following exact solution

on a square domain[0,1]2.The calculations are carried out on a set of uniform grids of{21×21,32×32,42×42,53×53,63×63,74×74,84×84,95×95,105×105}.The CCIRBF-Serial and-Parallel are considered to reach its steady state when its RMS is smaller than 10−9.The value of β =50 is chosen for calculations.Table 8 illustrates the proposed CCIRBF-Serial using 2×2 subdomains and CCIRBFParallel using 4×4 subdomains are able to produce the same solution accuracy to those of the CCIRBF-Single domain.For comparison purposes,we incorporate the standard central FDM and the HOC of Tian,Liang,and Yu(2011)into the two-level DD.Figure 14 shows that the proposed CCIRBF-Serial and-Parallel outperform the FDM-Serial and HOC-Serial in terms of solution accuracy.The solutions converge as O(h4.7)for the CCIRBF-Single domain,-Serial and-Parallel,O(h4.8)for the HOC-Serial,and O(h2.0)for the FDM-Serial.

Figure 14:Poisson equation,β=50:The effect of grid size h on the solution accuracy RMS.It is noted that the results for the CCIRBF-Single domain,CCIRBFSerial and CCIRBF-Parallel are indistinguishable.

An analysis of computational efficiency of the three algorithms,CCIRBF-Single domain,-Serial and-Parallel are illustrated in Table 9.Table 9 shows that the CCIRBF-Serial and-Parallel are generally much more efficient than the CCIRBFSingle domain.In term of computation time,the CCIRBF-Parallel generally uses less time to reach the same accuracy than the CCIRBF-Serial does.In term of efficiency,the CCIRBF-Serial is much more efficient than the CCIRBF-Parallel at low numbers of grids.However,the efficiency of the CCIRBF-Parallel increases and becomes better than that of the CCIRBF-Serial as the number of grids increases.

8.3 Navier-Stokes equation

To construct a test problem of the stream function-vorticity formulation with known solution,we specify the stream function described in[Richards and Crane(1979)]

on the unit square.The corresponding vorticity function,derived from(54),results in

The calculations are carried out on a uniform grid of 21×21.A wide range of Reynold numbers,Re=[10,30,50,70,90,120,150,200],is employed.The value of β =50 is chosen for calculations.Starting values of ω are analytic values of(71).To solve the steady vorticity equation,we utilise the vorticity equation(53),whereis a pseudo time-derivative term.The vorticity equation(53)is subjected to Dirichlet boundary condition derived from the exact solution of(71).We deliberately employ a small time step,∆t=10−6,to minimise the effect of the approximate error in time.The criterion to be satisfied for termination of the iteration scheme is given

Figure 15 shows numerical results produced by CCIRBF-Single domain,-Serial and-Parallel are much more accurate than those computed by the standard central FDM in Richards and Crane(1979).Table 10 shows the CCIRBF-Serial and-Parallel produce the same results with those of the CCIRBF-Single domain.

8.4 Lid driven cavity

The classical lid driven cavity has been considered as the test problem for the valuation of numerical methods and the validation of fluid flow solvers for the past decades.Figure 16 shows the problem definition and boundary conditions.The discretisation of the cavity domain is shown in Figure 17.

To derive the boundary conditions of the vorticity,the grid arrangement close to the bottom wall(j=1)is illustrated in Figure 18.Apply Taylor series up to second order for ψi,j=2[Biringen and Chow(2011)]

Figure 15:Navier Stokes problem with analytic solution,numerical solution using a grid of 21×21,β=50:The effect of Reynold number Re on the solution accuracy L1of vorticity(top)and on iteration number(bottom).It is noted that the results for the CCIRBF-Single domain,CCIRBF-Serial and CCIRBF-Parallel are indistinguishable.

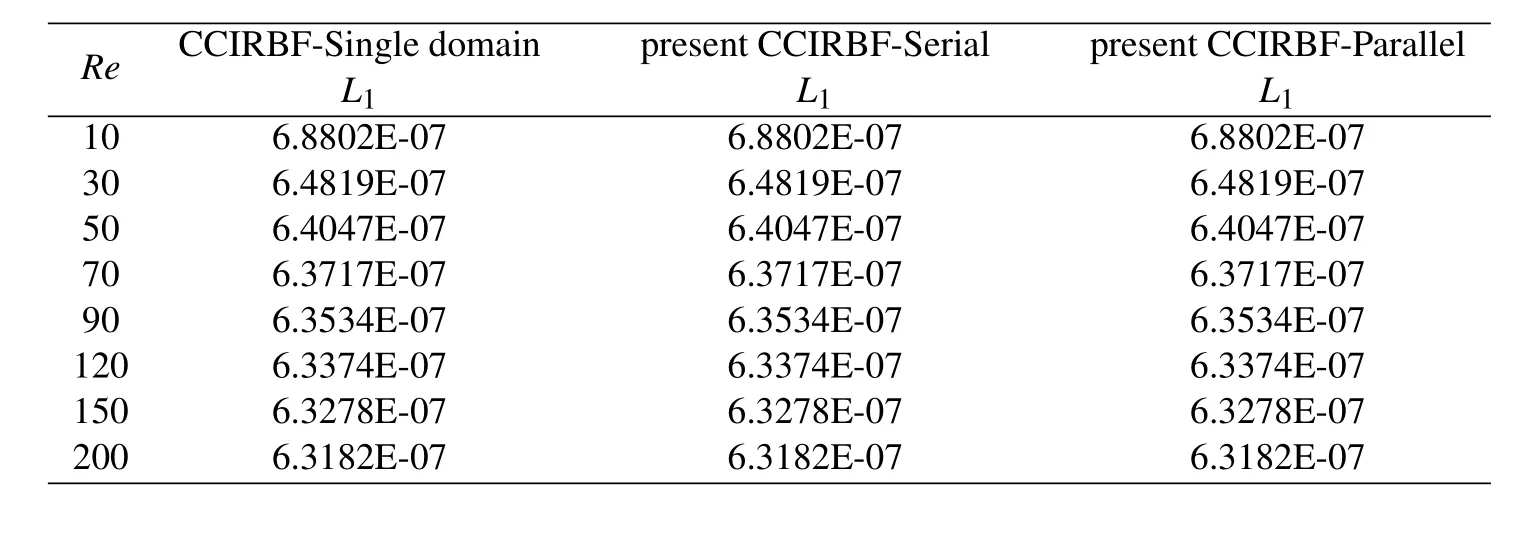
Table 10:Navier Stokes analytic solution,β=50:The effect of Reynold number Re on the solution accuracy RMS of vorticity.

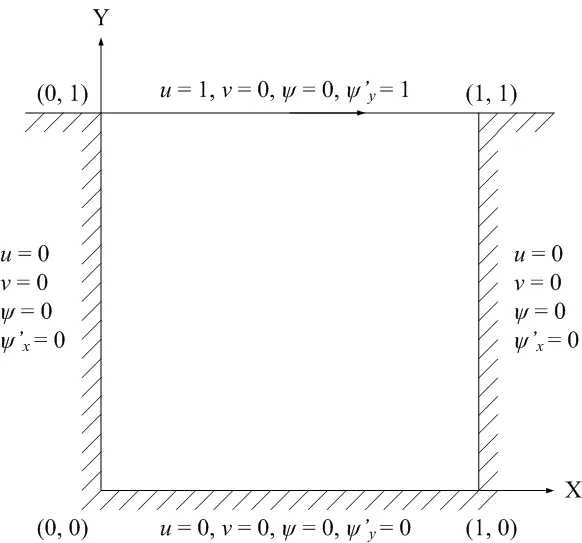
Figure 16:Lid driven cavity:problem con figuration and boundary conditions in terms of the stream function.

Figure 17:Lid driven cavity:domain discretisation.

Figure 18:Lid driven cavity:Grid arrangement close to the bottom wall.

Using

Equation(73)becomes

or

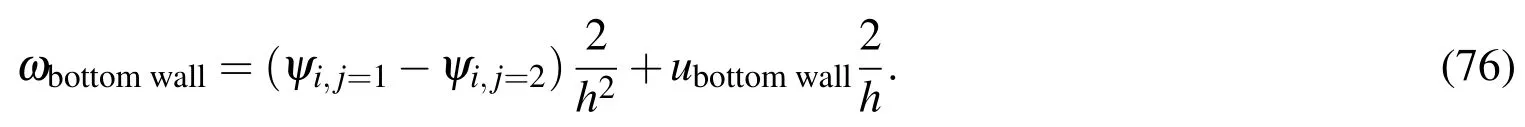
Similarly,at the top wall(j=ny)

At the left wall(i=1)

At the right wall(i=nx)

The numerical integration is done according to the following steps.

1.Set initial conditions at t=0(e.g.,at all interior points set

3.Compute interior points of velocities by calculating

4.Calculate(76)to(79)for boundary values ofusing

5.Find right hand side(RHS)of vorticity equation(58)

6.Compute interior values ofusing(58)

7.If a prescribed convergence criterion is reached,terminate the calculation;otherwise,go back to step 2.

Uniform grids of{11×11,31×31,41×41,51×51}and a range of Re∈{100,400,1000}are employed in the simulation.A fixed time step is chosen to be∆t=0.0001.Results of the present schemes are compared with some others[Ghia,Ghia,and Shin(1982);Gresho,Chan,Lee,and Upson(1984);Bruneau and Jouron(1990);Deng,Piquet,Queutey,and Visonneau(1994b);Botella and Peyret(1998);Sahin and Owens(2003);Thai-Quang,Le-Cao,Mai-Duy,and Tran-Cong(2012)].From the literature,FDM results using very dense grids presented by Ghia,Ghia,and Shin(1982)and pseudo-spectral results presented by Botella and Peyret(1998)have been referred as"Benchmark"results for comparison purposes.

Tables 11,12 and 13 show the present results for the extrema of the vertical and horizontal velocity pro files along the horizontal and vertical centrelines of the cavity for several Reynolds numbers.For Re=100(Table 11)and Re=1000(Table 13),the"Errors"are evaluated relative to"Benchmark"results of Botella and Peyret(1998).The results obtained by the present schemes are very comparable with others.

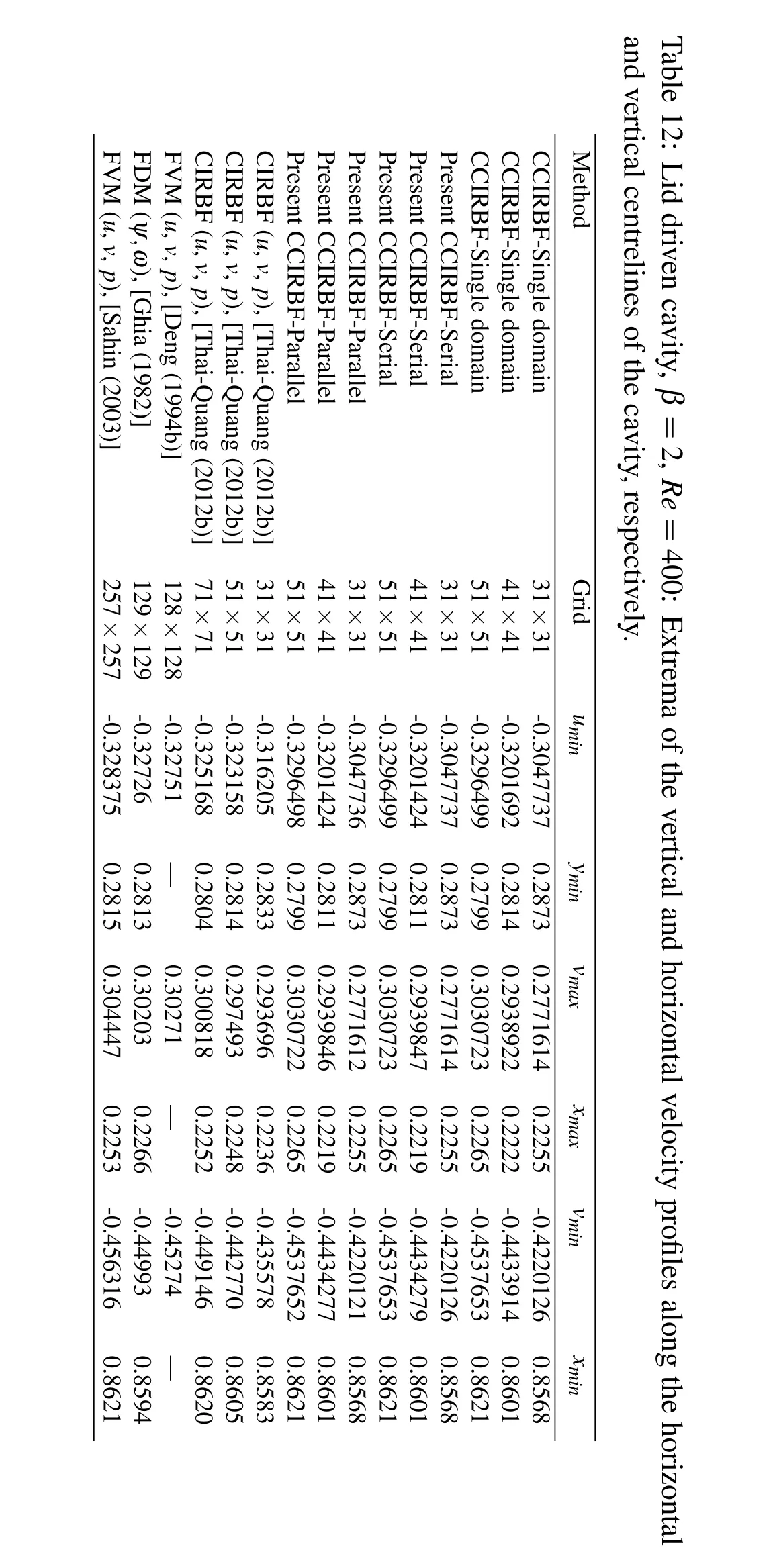
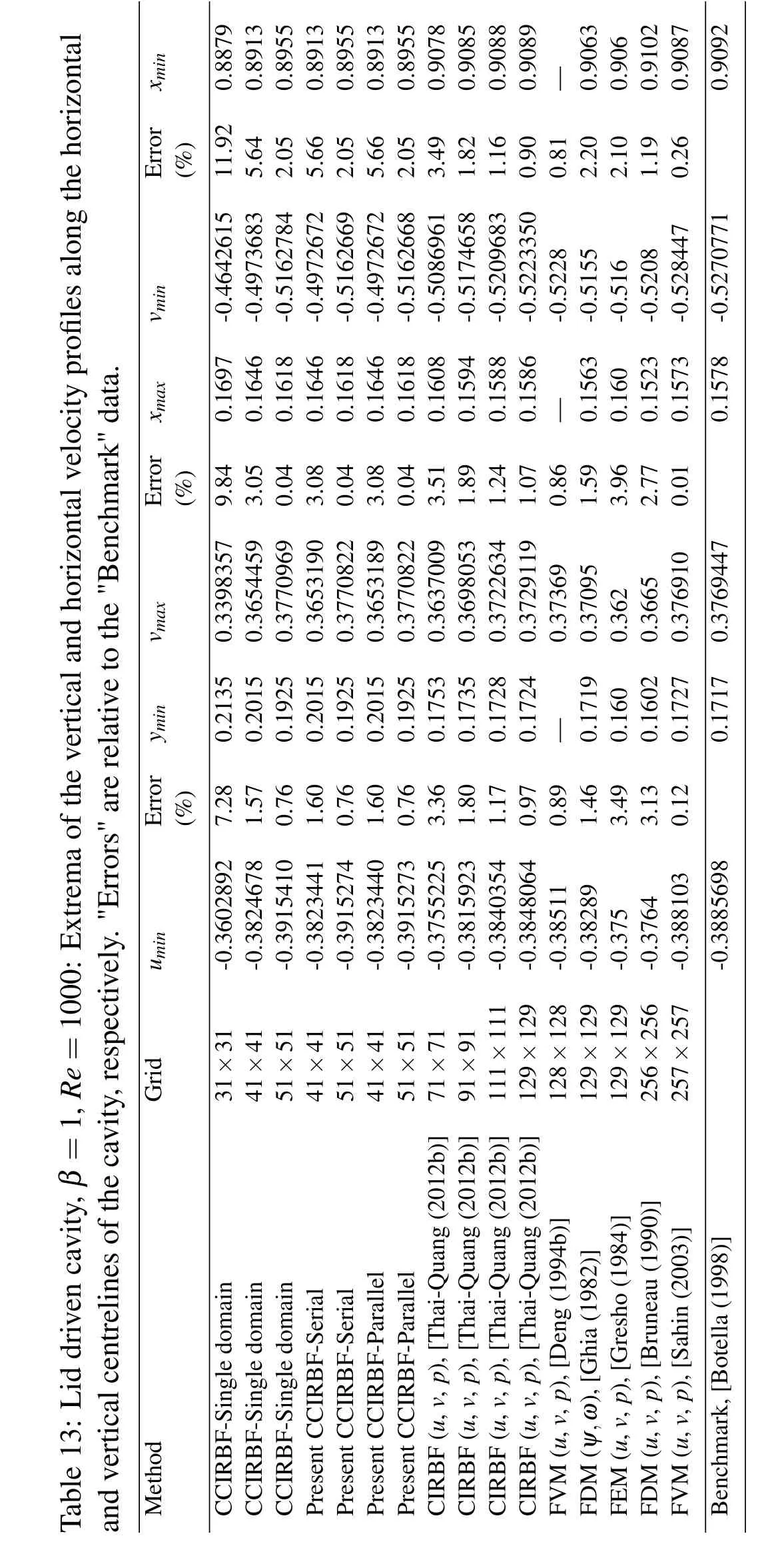
Figure 19:Lid driven cavity:Pro files of the u-velocity along the vertical centreline and the v-velocity along the horizontal centreline for Re=100(top),Re=400(middle)and Re=1000(bottom)with the grid of 51×51.

Figure 20:Lid driven cavity:Streamlines of the flow for Re=100(top),Re=400(middle)and Re=1000(bottom)with the grid of 91×91.The contour values used here are taken to be the same at those in[Ghia,Ghia,and Shin(1982)].

From Tables 11,12 and 13,we can observe the present scheme effectively achieves the benchmark results with fewer grids in comparison with the grids of some other methods used to obtain the benchmark results.In addition,those velocity pro files at Re∈{100,400,1000}with the grid of 51×51,are displayed in Figure 19,where the present solutions match the benchmark ones very well.The present scheme effectively achieves the benchmark results with fewer numbers of grids of 51×51 in comparison with the grid of 129×129 used to obtain the benchmark results in[Ghia,Ghia,and Shin(1982)].

To exhibit contour plots of the flow,a range of Re∈{100,400,1000}and the grid of 91×91 are employed.Figures 20 and 21 show streamlines and iso-vorticity lines,

Figure 21:Lid driven cavity:Iso-vorticity lines of the flow for Re=100(top),Re=400(middle)and Re=1000(bottom)with the grid of 91×91.The contour values used here are taken to be the same at those in[Ghia,Ghia,and Shin(1982)].

which are derived from the velocity field.These plots are also in good agreement with those reported in the literature.

For simplicity,the results of CCIRBF-Parallel are chosen to be plotted in Figures 19,20 and 21.It is noted that the results of CCIRBF-Serial and-Parallel are indistinguishable.

Table 14 shows the indicative comparison of computational efficiency of the CCIR BF-Single domain,-Serial and-Parallel for the case of Re=100 with various numbers of grids.The CCIRBF-Serial and-Parallel are more efficient to be compared with the CCIRBF-Single domain.

9 Concluding remarks

In this work,we carry out a convergence analysis for different types of domain decomposition(DD)preconditioners implemented with the coupled compact integrated RBF(CCIRBF).The performance of the present CCIRBF based algorithms are analysed in terms of the iteration count with different mesh sizes,number of subdomains and overlap sizes.The numerical results show that

i.the present CCIRBF two-level multiplicative algorithm is the best one compared with the other present CCIRBF based algorithms.

ii.the present CCIRBF two-level multiplicative algorithm is better than the HOC two-level multiplicative algorithm for the case of 1%and 25%overlaps.For other overlap cases,the present CCIRBF two-level multiplicative algorithm is comparable with the HOC two-level multiplicative algorithm.

In the implementation of the present CCIRBF in the DD preconditioners,we found that the incorporation of a coarse mesh problem into the multiplicative preconditioner is necessary to obtain a significant reduction in the computational iteration count.The present CCIBRF two-level multiplicative method yields small iteration counts over a wide range of numbers of subdomains,grid sizes and overlap sizes in our examples.

The present work introduces highly accurate serial and parallel algorithms using the CCIRBF for heat and fluid flow problems.The beauty of the proposed serial and parallel schemes is that they are able to produce almost the same level of accuracy as that of the single domain scheme.In computational examples,the results produced by serial and parallel algorithms are very compatible with other methods such as finite element method(FEM)and finite difference method(FDM).The capability of producing the stable and highly accurate results of the proposed algorithms is due to the utilisation of the coarse mesh of the two-level DD and the CCIRBF approximation.The serial and parallel algorithms offer a divideand-conquer solution for large-scale partial differential equation(PDE)problems.Therefore,the proposed algorithms may be used as alternatives to the single domain scheme to solve large-scale problems which the single domain scheme is generally struggling to solve due to its ill-conditioned or fully populated companion matrix.

Acknowledgement:The first author would like to thank USQ for an International Postgraduate Research Scholarship.

Atluri,S.N.;Zhu,T.(1998): A new meshless local petrov-galerkin(mlpg)approach in computational mechanics.Computational Mechanics,vol.22,no.2,pp.117–127.

Babuska,I.;Melenk,J.M.(1997):The partition of unity method.International Journal for Numerical Methods in Engineering,vol.40,no.4,pp.727–758.

Behr,M.(2014): Gmres usage,chair for computational analysis of technical systems.http://www.cats.rwth-aachen.de/library/research/technotes.

Belytschko,T.;Krongauz,Y.;Organ,D.;Fleming,M.;Krysl,P.(1996):Meshless methods:An overview and recent developments.Computer Methods in Applied Mechanics and Engineering,vol.139,no.1-4,pp.3–47.

Belytschko,T.;Lu,Y.Y.;Gu,L.(1994):Element-free galerkin methods.International Journal for Numerical Methods in Engineering,vol.37,pp.229–256.

Biringen,S.;Chow,C.(2011):Anintroduction tocomputational fluid mechanics by example.John Wiley and Sons,Hoboken,New Jersey,US.

Botella,O.;Peyret,R.(1998): Benchmark spectral results on the lid-driven cavity flow.Comput.Fluids,vol.27,no.4,pp.421–433.

Bruneau,C.;Jouron,C.(1990):An efficient scheme for solving steady incompressible navier-stokes equations.J.Comput.Phys.,vol.89,pp.389–413.

Cai,X.(2003): Advanced Topics in Computational Partial Differential Equations,volume 33 of Lecture Notes in Computational Science and Engineering.Springer,Berlin,Germany.

Chen,Y.;Lee,J.;Eskandarian,A.(2006):Meshless Methods in Solid Mechanics.Springer,NY 10013,USA.

Danaila,I.(2007):An introduction to scientific computing:twelve computational projects solved with MATLAB.Springer,NY 10013,USA.

Deng,G.;Piquet,J.;Queutey,P.;Visonneau,M.(1994b): Incompressibleflow calculations with a consistent physical interpolation finite-volume approach.Comput.Fluids,vol.23,no.8,pp.1029–1047.

Ghia,U.;Ghia,K.;Shin,C.(1982):High-resolutions for incompressible flows using navier-stokes equations and a multigrid method.J.Comput.Phys.,vol.48,pp.387–411.

Gresho,P.;Chan,S.;Lee,R.;Upson,C.(1984): A modified finite element method for solving the time-dependent,incompressible navier-stokes equations.part 2:Applications.Int.J.Numer.Meth.Fluids,vol.4,pp.619–640.

Jenkins,E.W.;Kees,C.E.;Kelley,C.T.;Miller,C.T.(2001):An aggregationbased domain decomposition preconditioner for groundwater flow.SIAM Journal on Scientific Computing,vol.23,no.2,pp.430–441.

Kansa,E.(1990a):Multiquadrics - a scattered data approximation scheme with applications to computational fluid-dynamics-i.surface approximations and partial derivative estimates.Computers and Mathematics with Applications,vol.19,no.8/9,pp.127–145.

Kansa,E.(1990b):Multiquadrics - a scattered data approximation scheme with applications to computational fluid-dynamics-ii.solutions to parabolic,hyperbolic and elliptic partial differential equations.Computers and Mathematics with Applications,vol.19,no.8/9,pp.147–161.

Lancaster,P.;Salkauskas,K.(1981): Surfaces generated by moving least squares methods.Mathematics of Computation,vol.37,no.155,pp.141–158.

Li,J.;Cheng,A.H.D.;Chen,C.S.(2003): A comparison of efficiency and error convergence of multiquadric collocation method and finite element method.Engineering Analysis with Boundary Elements,vol.27,pp.251–257.

Liu,W.K.;Chen,Y.;Chang,C.T.;Belytschko,T.(1996): Advances in multiple scale kernel particle methods.Computational Mechanics,vol.18,no.2,pp.73–111.

Lucy,L.B.(1977):A numerical approach to the testing of the fission hypothesis.The Astronomical Journal,vol.82,no.12,pp.1013–1024.

Mai-Duy,N.;Tran-Cong,T.(2001a): Numerical solution of differential equations using multiquadric radial basis function networks.Neural Networks,vol.14,no.2,pp.185–199.

Mai-Duy,N.;Tran-Cong,T.(2001b):Numerical solution of navier-stokes equations using multiquadric radial basis function networks.International Journal for Numerical Methods in Fluids,vol.37,no.1,pp.65–86.

Mai-Duy,N.;Tran-Cong,T.(2003):Approximation of function and its derivatives using radial basis function networks.Applied Mathematical Modelling,vol.27,no.3,pp.197–220.

Mai-Duy,N.;Tran-Cong,T.(2005):An efficient indirect rbfn-based method for numerical solution of pdes.Numerical Methods for Partial Differential Equations,vol.21,pp.770–790.

Nayroles,B.;Touzot,G.;Villon,P.(1992): Generalizing the finite element method:Diffuse approximation and diffuse elements.Computational Mechanics,vol.10,no.5,pp.307–318.

Niyogi,P.;Chakrabartty,S.;Laha,M.(2009): Introduction to computational fluid dynamics.Dorling Kindersley,482,F.I.E.,Patparganj,Delhi 110 092,India.

Quarteroni,A.;Valli,A.(1999): Domain decomposition methods for partial differential equations.Clarendon Press,Oxford.

Richards,C.;Crane,C.(1979): The accuracy of finite difference schemes for the numerical solution of the navier-stokes equations.Applied Mathematical Modelling,vol.3.

Saad,Y.;Schultz,M.(1986): Gmres:A generalized minimal residual algorithm for solving nonsymmetric linear systems.SIAM Journal on Scientific and Statistical Computing,vol.7,pp.856–869.

Sahin,M.;Owens,R.(2003):A novel fully implicit finite volume method applied to the lid-driven cavity problem-part i:High reynolds number flow calculations.Int.J.Numer.Meth.Fluids,vol.42,pp.57–77.

Smith,B.F.;Bjorstad,P.E.;Gropp,W.D.(1996): Domain Decomposition Parallel Multilevel Methods for Elliptic Partial Differential Equations.Cambridge University Press,NY 10011-4211,USA.

Strang,G.(2007): Computational science and engineering.Wellesley-Cambridge Press,MA 02482,USA.

Thai-Quang,N.;Le-Cao,K.;Mai-Duy,N.;Tran-Cong,T.(2012): A highorder compact local integrated-rbf scheme for steady-state incompressible viscous flows in the primitive variables.CMES:Computer Modeling in Engineering and Sciences,vol.84,no.6,pp.528–557.

Thai-Quang,N.;Mai-Duy,N.;Tran,C.-D.;Tran-Cong,T.(2012):High-order alternating direction implicit method based on compact integrated-rbf approximations for unsteady/steady convection-diffusion equations.CMES:Computer Modeling in Engineering and Sciences,vol.89,no.3,pp.189–220.

Tian,Z.;Liang,X.;Yu,P.(2011): A higher order compact finite difference algorithm for solving the incompressible navier stockes equations.International Journal for Numerical Methods in Engineering,vol.88,pp.511–532.

Tien,C.M.T.;Thai-Quang,N.;Mai-Duy,N.;Tran,C.-D.;Tran-Cong,T.(2015): A three-point coupled compact integrated rbf scheme for second-order differential problems.CMES:Computer Modeling in Engineering and Sciences(Accepted).

Toselli,A.;Widlund,O.(2005): Domain Decomposition Methods-Algorithms and Theory.Springer,Berlin,Germany.

Zerroukat,M.;Power,H.;Chen,C.S.(1998): A numerical method for heat transfer problems using collocation and radial basis functions.International Journal for Numerical Methods in Engineering,vol.42,pp.1263–1278.

1Computational Engineering and Science Research Centre,Faculty of Health,Engineering and Sciences,The University of Southern Queensland,Toowoomba,Queensland 4350,Australia.