The Direction Zone of Engineless UAVs in Dynamic Soaring

B.J.Zhu,2,Z.X.Hou,Y.F.Luand S.Q.Shan

The Direction Zone of Engineless UAVs in Dynamic Soaring

B.J.Zhu1,2,Z.X.Hou1,Y.F.Lu1and S.Q.Shan1

This paper mainly analyzes the dynamic soaring of UAV utilizing gradient wind.Dynamic soaring is an Efficient path in which UAV absorbs energy from environment to enhance its flight endurance.A set of three-dimensional point dynamic equations for a soaring aircraft in three degrees of freedom is used in calculations.To simplify the calculation,the gradient wind’s direction is taken into decomposition.The notion of trajectory subsection analysis is applied to account for the energy transformation mechanism during the dynamic soaring,and the zone of direction is converted into cutting-in angle,which is regarded as initial limiting condition in the optimization of dynamic soaring trajectory.Then,the relationship between energy gain/loss and cutting-in angle is acquired.Three dynamic soaring styles corresponding to three typical cutting-in angles are selected to be analyze intensively,and the explicit characters of trajectories,airspeed,attitude angles and energy variation are presented.All these results reveal the zone of direction and validate the method of control for a dynamic soaring UAV soaring in gradient wind field without thrust.

dynamic soaring, flight endurance,cutting-in angle,gradient wind,UAV.

1 Introduction

Unmanned aerial vehicles(UAVs)are attractive for a wide range of applications on human activity.Long-endurance flight is a key factor of UAVs utility[Stephen,Kenheth,Peter and Linton(2005)].Be limited by fuel capacity,UAVs’longendurance flight is difficult to be achieved.Nowadays,the UAVs’ flight endurance can be improved by the progress of power capacity,aerodynamic and engine design[Zhao and Qi(2004)].However,another important option for enhancing UAVflight endurance is to seek for energy from flight environment,such as absorbing energy from gradient wind field.Extracting energy from the gradient wind to enhance flight capability is generally referred to as dynamic soaring[Bower(2011)].According to the observation data,there are different wind gradients at different altitude ranges.The average strength and direction of wind in most of places below altitude of 30km is shown in Fig.1.It indicates that there are several persistent wind shears which can be possibly used to power the flight of dynamic soaring at different altitude ranges.The experimental data of Fig.1 was acquired by sounding balloon.

As a matter of fact,there are many large-sized birds that make use of gradient wind to enhance their flight ability in the nature,e.g.the albatross[Richardson(2010);Denny(2009)].The Wandering Albatross lives predominantly in Kerguelen Archipelago of the southern hemisphere,and utilizes dynamic soaring to travel throughout the South Ocean with little propulsive energy expenditure[(Sachs,Traugott and Nesterova(2012);Traugott,Holzapfel and Sachs(2010)].Early in 1883,Rayleigh(1883)published “The soaring of birds”on the Nature,which is regarded as the first paper about dynamic soaring.

Dynamic soaring is an important flight technique designed to allow aircraft to extract energy from atmosphere.So far,the dynamic soaring has been focused on extensively and some scholars have studied it intensively mainly about wind estimate,path planning and energy variation in dynamic soaring.Lawrance and Sukkarieh(2011a,2011b,2009)studied autonomous soaring flight for UAV,whose contributions include the analysis of gliding flight in a structured framework and the design of a path planning architecture for autonomous dynamic soaring in unknown wind field.In order to estimate wind field for autonomous dynamic soaring,Lawrance(2011c)provided a method for taking direct observations of the wind during flight and creating a wind to direct future exploration.Langelaan,Spletzer and Montella(2012)estimated wind field by using a polynomial parameterization of the wind field.Based on the relationship between attitude and linear acceleration,Zuo(2012)proposed an adaptive trajectory tracking control algorithm to estimate unknown aerodynamic parameter.As to energy variation in dynamic soaring,Chakrabarty and Langelaan(2010)presented an approach to planning long distance autonomous soaring trajectories for small uninhabited aerial vehicles harvesting energy from the atmosphere,predicted optimal energy Efficient routes from a given wind field data.Bower(2011)studied the energy transfer mechanisms for a vehicle flying in a spatially and temporally varying wind field.Deitter,Richards and Toomer(2009)studied optimal trajectories for minimal and maximal wind conditions,and worked out the trajectories for optimal cross-country travel.In order to simplify the optimization problem,the flight model’s differential flatness property is used.Bonnin and Toomer(2013)analyzed the feasibility to use dynamic soaring,and the characteristic phases of flight were evidenced out of overall trajectory.Sachs,Lesch and Knoll(1989)used a numerical multiple shooting approach to investigate realistic nonlinear wind gradient.Clarence(1964)analyzed the dynamic soaring flight of albatross with mathematical models.

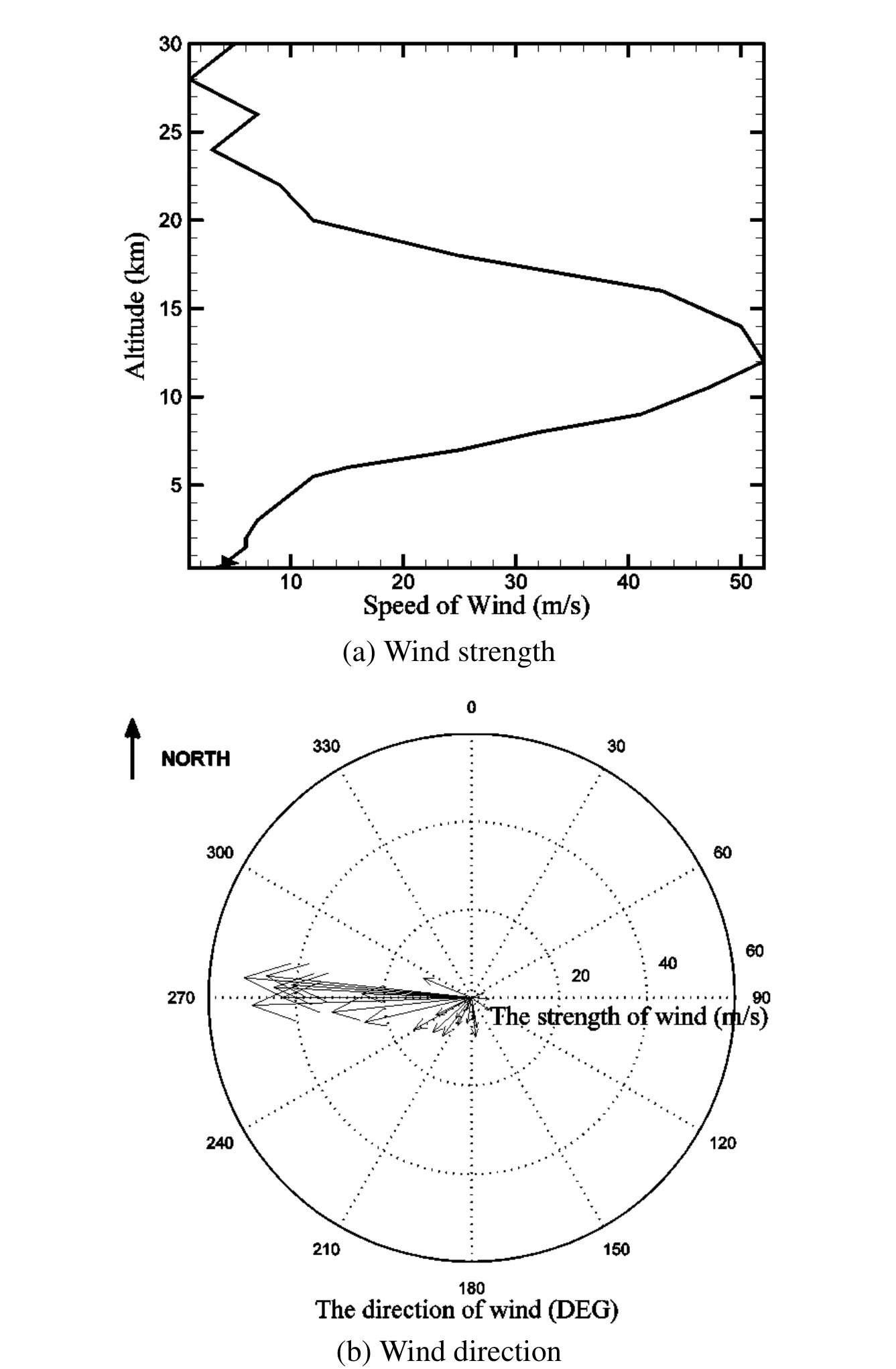
Figure 1:The experimental data of wind strength and direction.

Scores of research findings reveal the significant meaning of dynamic soaring.However,the background of these achievements underlines that the trajectory planning and the energy-harvesting in dynamic soaring are multiple and difficult to be realized.In the given wind field,the UAV can fly without thrust and be kept balanced between income and expenditure of total energy determined the direction zone of dynamic soaring trajectory.Based on the achievements of energy variation and trajectory planning in dynamic soaring from the research findings mentioned above,this paper converts the direction zone into the cutting-in angle,and takes advantage of subsection analysis to analyze optimal trajectories for energy balance in a cycle of dynamic soaring.The maximum cutting-in angle is analyzed,and three typical cutting-in angles corresponding to the three trajectories,airspeed,attitude angles and energy variation of each trajectory are investigated.

The rest of the paper is organized as follows:Modeling and analysis are introduced in Section 2.Simulation results and associated discussion are given in section 3.Finally,the concluding remarks are made in Section 4.

2 Modeling and Analysis

2.1 The model of wind field

It is the shear that the aircraft uses to gain energy when following a favorable dynamic soaring trajectory.Thus,an accurate model of the wind pro file is desirable.From Fig.1,a logarithmic profile is chosen as this model matches the measurements near the surface of the earth(about 0～100m).The logarithmic pro file is defined as follow[Sukumar and Selig(2010);Bencate and Sousa(2011)]:

Where W(h)is the wind speed at height h,and Wrefis the wind speed at the reference height href.The variable h0is the aerodynamic roughness length or the roughness factor.It is an experimentally derived constant that accounts for the kind of surface over which the wind is blowing.Typically,a higher value of the roughness length indicates more obstructions on the surface such as trees and buildings.After the regulation of parameters,the fitting curve of experimental data in 0～100m is shown in Fig.2.

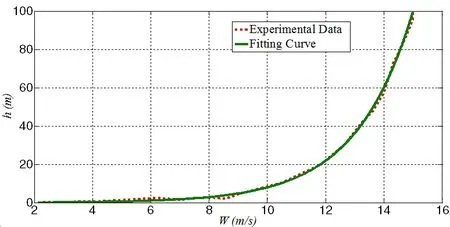
Figure 2:Wind speed vs.height.

In Fig.2 the fitting curve shows wind pro files for value of the roughness coefficient with Wref=15m/s,href=100m,h=0.05m All these factors match well with the wind pro files near the surface of the earth(about 0～100m),and are adopted throughout the following of this paper.

2.2 Dynamic Soaring Model

In this section the dynamic equation for a soaring aircraft in three degrees of freedom(3DOF)is discussed.As the rotational dynamics are assumed to be far faster than the translational dynamics,the rotations are not considered in the flight model[Deitter,Richards and Toomer(2009)].It is assumed that there is no propulsion system on the aircraft.For a point mass model,the forces and angles used in this model are shown in Fig.3.The inertial wind speed components in the x,y,and z directions are respectively denoted as Wx,Wyand Wz.Note that Wy=Wz=0,Wxis the function of wind.

In Fig.3,there are three applied forces accounted for in this model:lift(L),drag(D)and gravitational force(mg), γ is flight path angle,ψ is heading angle,φ is bank angle,Varepresents the air speed.

Applying Newton’s 2nd law to analyze the forces acted on the aircraft,the results are shown in Eqs.2:

Figure 3:Air-relative velocity and applied forces for the UAV.

The kinematic equations are given by Eqs.3:

The kinematic equation(Eqs.3)is differentiated with respect to time,and the following equations can be obtained.

Combining Eqs.2 and Eqs.4,then there is:

Associated with wind model in section 2.1,the gradient wind field of the experiment ground where the horizontal wind speed increases in logarithm form.So Wxincrease in the form of logarithm in the altitude.

Combining Eq.(5)and Eq.(6),there is:

In dynamic soaring,Equations(4)can be used as a model for the simulation of an aircraft flying through a known gradient wind field.These equations can also act as restriction equations in dynamic soaring.Once the zone of altitude angle is determined,the optimized trajectory of dynamic soaring can be acquired.Eq.(7)is the change rate of Va,which is used widely in the next section.

2.3 Dynamic soaring route and energy-harvesting process

In order to figure out the energy transformation mechanism during the dynamic soaring,the notion of subsection analysis is applied.In Fig.4,the dynamic soaring cycle is divided into four phases:the UAV starts with initial conditions at point“A”,turns into the wind field and begins the climbing with headwind on[AB],then turns in high altitude on the curve[BC],follows the UAV with tailwind on[CD],finally turns in low altitude on the curve[DE].The subsection analysis of dynamic soaring trajectory is inspired from Bonnin and Toomer(2013),in whose paper,the optimal closed trajectory consists 8-shaped path.

Figure 4:The illustration trajectory of dynamic soaring.

In Fig.4,the UAV is flying to windward,with the flight direction parallel to the wind.When there is an included angle between the wind and the UAV’s heading,the wind’s direction needs to be taken into decomposition to simplify the analysis.As indicated in Fig.5,one component of wind direction parallels to the UAV heading when UAV is climbing with headwind,while another one parallels to the UAV’s heading when the UAV is gliding with tailwind.

Figure 5:The decomposition of the gradient wind’s direction.

Figure 6:The decomposition of the gradient wind’s direction as seen from above the hydrostatic level.

In this paper,the included angle between the wind and the UAV’s heading is named as cutting-in angle.In Fig.5 and Fig.6,λ is the cutting-in angle.Wx1is the horizontal component of the gradient wind which parallels to UAV’s horizontal heading and the UAV is climbing with headwind.Wx2is the other horizontal component of the gradient wind which parallels the UAV’s horizontal heading and the UAV is gliding with tailwind.The value of Wx1and Wx2can be calculated by Eqs.8.In this case,the angle of the UAV’s turning in high altitude is π −λ −α,and the angle of the UAV’s turning in low altitude is λ +α The chosen of angle to be used depends on the relationship between the soaring route and energy absorbed.

On the curve[AB],the UAV climbs with the headwind through a zone where the wind gradient is the strongest,along with the increase of the UAV’s altitude,the UAV’s airspeed decreased.Seemingly,the decreasing of airspeed will lead to the consequence that the lift cannot provides a positive contribution to overcome the influences of drag and gravity,but with the change of attitude angles,the increasing of lift factor would make the UAV still has enough lift during the climbing with the headwind.In the process of flight,the UAV mainly relies on the lift from airspeed,so the kinetic energy can be calculated by airspeed.The initial energy can be represented as:

where E1is initial energy of the UAV,Va,1is the initial airspeed.In the initial stage,the potential energy is considered as 0.

With increasing of the UAV’s altitude,the energy of the UAV can be expressed as:

h is the flight altitude,Va,2is the UAV’s airspeed at h.

The variation of the energy is:

By differentiating Eq.11,the power equation can be obtained:

Combining Eq.(7),Eq.(8)and Eq.(12),there is:

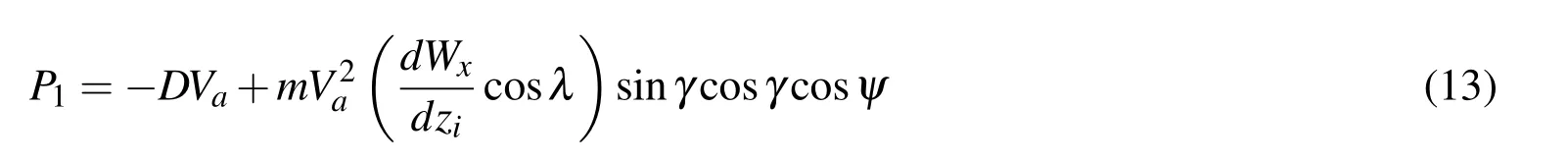
In Eq.(13),if P1＞0,it means the UAV can gain energy from the wind field,while P1＜0 indicates the UAV losses energy during the flying process.And it can also be found that a large range of the gradient of the windexists,which means the UAV can acquire more energy from the wind field.

On the curve[BC],the UAV makes a turning in the high altitude.Seen from above the hydrostatic level,the dynamic soaring trajectory in three-dimensional pointmass can be described as flight trajectory in two-dimensional point-mass.The twodimension flight trajectory is illustrated in Fig.6.

Figure 7:The two-dimension flight trajectory of dynamic soaring,which is seen from above.

In Fig.6 and Fig.7,it’s assumed that the initial speed of the turning in high altitude is VR1,the direction angle of the UAV have changed λ,and the circumferential velocity turn into VR2,During the course of the turning,take the wind speed into consideration,at the point B and C,the actual air speed of the UAV can be expressed as:

The variation of the energy during the turning in the high altitude is:

Equation(15)can be written as,

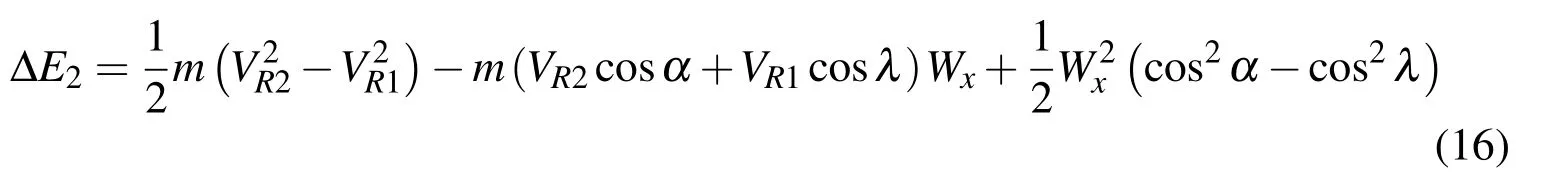
During the turning in the high altitude,the work done by the centripetal force F can be represented as:

Let θ=ωt,ω is the angular velocity of the turning.

And

So

If the UAV keeps the circumferential velocity at a constant value,such as VR1,the work done by the centripetal force F can be expressed as:

If the UAV is flying at the direction of the wind,shown as the flight route of Fig.5,λ=α=0˚,the work done by the centripetal force isIn this case,from Eq.(16),it can be found that.Then,the centripetal force can be regarded as the cause of the variation of the energy during the turning in the high altitude.So,

Because of the variation of the circumferential velocity and the cutting-in angle,the energy saved by VR1,VR2,λ and α can be written as:

From Eq.(23),it can be found that the energy saved by the variation of the circumferential velocity is related to the speed difference and the value of cutting-in angle.

The curve[CD]is almost the same as the curve[AB].The UAV glides with tailwind through a zone where the wind gradient is the strongest.Along with the decline of the UAV’s altitude,the UAV’s ground speed increases.The direction of the ground speed is inversed to the wind.The airspeed of the UAV can be expressed as:is the ground speed of the UAV,Wx(Z)is the wind speed at different altitude.With the decreasing of the altitude,the ground speed increases,while the wind speed decreases.So the airspeed increases distinctly compared with no gradient wind in the flying environment.If the UAV’s initial energy during the course of the gliding with tailwind is E3,E3can be expressed as:

With the decreasing of the UAV’s altitude,the energy of the UAV can be indicated as:

The variation of the energy is:

By differentiating Eqs.26,the power equation can be obtained:

Combining Eq.(7),Eq.(8)and Eq.(27),there is:

From Eq.(28),if P3＞0,that is to say the UAV can gain energy from the wind field,and P3＜0 represents the UAV losses energy during the flying course.And a large range of the gradient of the windcan be found,which indicated that the UAV can acquire more energy from the wind field.

On the curve[DE],the UAV make the turning in low altitude.From the analysis of wind field model,it is almost the still air in the low altitude.So it can be assumed that Wx=0 m/s.But there still has the air drag that causes energy loss.The applied forces analysis for the UAV is shown in Fig.8.

In Fig.8,φ is the angle of bank, γ is flight path angle.The connection between lift(L),drag(D)and mass(m)can be expressed as:

Figure 8:Applied forces analysis for the aircraft.

S is the wing area of the UAV.Combining Eqs.(29)-(31),gives:

The energy lost throughout the cycle due to drag is computed using Eq.34,

where,ψ is the heading angle

So the energy lost per heading angle change is:

Accordingly,Eq.(36)is used to calculate the energy lost in the course of the turning into low altitude,with the value of ψ replaced by λ + α The variation of the energy of turning in low altitude is:

After a cycle of dynamic soaring,the whole energy of UAV can be represented as:

If E=0,the UAV can fly in the wind field without energy.

3 Simulation and Discussion

Intrinsically,dynamic soaring is a difficult natural pattern to simulate,because trajectories need to be very precise.The parameters of the UAV demonstrator are given in Table 1.

Table 1:The UAV demonstrator parameter values used.

This is a small UAV,which is designed by referring to the shape of a Wandering Albatross.According to the parameters of UAV,the dynamic soaring model is emulated by means of MATLAB.The toolbox used for the simulation is GPOPS(General Pseudospectral Optimal control Software).The GPOPS library uses SNOPT to perform the optimization.

In this paper,in order to find out the scope of cutting-in angle,it’s designed that each established cut-in angle corresponds to an optimal trajectory.During the optimal trajectory,the UAV can accomplish a cycle of dynamic soaring without propulsive thrust.The goal of the trajectory optimization problem is to find out the state and control angles that minimize or maximize a selected cost function while satisfying the equations of kinetics(see Eqs.(2)).

The cost function in this paper is designed to maximize the energy-extraction,and make sure the final energy approximate to the initial energy after a cycle of dynamic soaring.There are four optimization weight coefficients of the four flight periods,which are ω1,ω2,ω3,ω4.This gives the following optimization problem and constrains conditions.

subject to

In this paper,the optimal trajectories are periodic in some or all of the state variables,although the positions are not required periodicity,and all other states will have the periodic boundary conditions imposed.So the optimal trajectories in fixed wind conditions are repeatable neutral energy cycles.E is a target function,which defines the constraints on the aircraft dynamics soaring.Eq.(41),Eq.(42)and Eq.(43)together ensure that aircraft always proceeds forward along the trajectory.Eq.(44)de fines the airspeed limits.

The event script defines the partial derivatives of each event constraint with respect to the initial state,initial time, final state, final time,and parameters.The boundary conditions are expressed as follows:

In order to solve this problem,a collocation approach technique is used.In this method,the optimal trajectory is discretized into a number of intervals,which are regularly distributed in time.The discretized dynamical equations are satisfied at the midpoint of the time interval.The constraint equations are given as following,from Eq.(46),it can estimate the state vector at the midpoint.

The equality constraint corresponding to each state variable is expressed as in Eq.(48).

Where,k is the number of collocation points.

Each UAV has controllable boundary[Bonnin and Toomer(2013)].The path constraints are given in Eqs.(49),which is enforced at the series of discrete time points as bounds on the solution parameters.

In order to find out the maximum cutting-in angle,a series of dynamic soaring emulation experiments are made.The connection between the cutting-in angle and the energy gain/loss is shown in Fig.9.

From Fig.9(a),it can be found that with the increasing of the cutting-in angle,the energy gain/losses is increased at the same time,and the energy gain is equal to the energy losses.The value of 32˚is the critical point of the cutting-in angle.If the cutting-in angle is greater than 32˚,the energy gain will descend rapidly.In other word,the energy gain from the environment cannot support the energy losses.In this case,the UAV cannot soaring in the wind field without propulsive thrust.During the simulation,each λ has a special α,and the connection between λ+α and the energy gain/loss is described in Fig.9(b).

In order to examine the effects of different cutting-in angles on optimal dynamic soaring route,three different values of cutting-in angles are used.The principle is divided the zone of cutting-in angle into three portions.

Figure 9:Energy gain/losses with the change of λ and λ +α,and correspond to each λ and λ +α,the UAV has finished a cycle of dynamic soaring.

Fig.10 shows a three-dimensional view of three kinds of routes corresponding to the three different values of cutting-in angles.The initial points of three routes are all the sam

In Fig.10,Route 1 stands for the cutting-in angleThe maximum flight altitude of UAV is about 25m,which is the simplest style in dynamic soaring;Route 2 stands for the cut-in angle λ=16˚,and α=15˚.The maximum flight altitude of UAV is about 28m;Route 3 stands for the cut-in angle λ=32˚,and α=31˚,the maximum flight altitude of UAV is about 35m.It’s the critical state of dynamic soaring without propulsive force.For λ＞32˚,the UAV cannot carry out normal dynamic soaring.

Figure 10:Three types of dynamic soaring cycle.Wind blows in the position X direction,with magnitude increasing logarithmic with altitude.

In three values of cutting-in angles,the original speed of the UAV is 30m/s.Fig.11 shows the airspeed variation corresponded to three routes.It can be found that the airspeed variation trend of three routes is almost in the same.The airspeed reaches the minimum at the peak altitude and reaches the maximum at the lowest altitude.After a cycle of dynamic soaring,the airspeed regains the original speed.That is to say,there is no energy dissipation after a cycle of dynamic soaring.And in the viable scope of cutting-in angle,the bigger cutting-in angle,the more time should be needed for a cycle of dynamic soaring.

Figure 11:Airspeed for the model UAV in simulation.

During three kinds of routes,the lift coefficient variation of each flying routes are shown in Fig.12.The lift coefficient variation trends of three flying styles are almost the same.When the UAV reaches the peak altitude,the lift coefficient reaches the maximum.At this point,UAV’s airspeed reaches the minimum value.So the UAV still has enough lift for flight during the turning in the high altitude.

Figure 12:The lift coefficient for the UAV flying through a log cycle.

In three dynamic soaring cycles,the aircraft’s flight path angle(γ)and bank angle(φ)are shown in Fig.13 and Fig.14 respectively.

Examining the Fig.13,the flight path angles of three trajectories express the same variation trend.That is to say,in a known gradient wind field,the flight path angle isn’t the key influencing factor of different trajectories.In Fig.14,each cuttingin angle has a special initial bank angle.Combining Fig.6 and Fig.7,with the increasing of cutting-in angle,and decreasing Wx1,the airspeed decreasing,the UAV need a special bank angle to provide enough lift.

Fig.15 plots the heading angles variation of three routes.From Fig.15,it can be found that the initial heading angles equal the cutting-in angles,and the heading angles represent the flying direction of UAV in dynamic soaring.

For three kinds of trajectories presented in Fig.10,the evolution of air relative total energy with time of each trajectory is depicted in Fig.16.

Figure 13:The flight path angle(γ)for the UAV flying through a log cycle.

Figure 14:The bank angle(φ)for the UAV flying through a log cycle.

Figure 15:The heading angle(ψ)for the UAV flying through a log cycle.

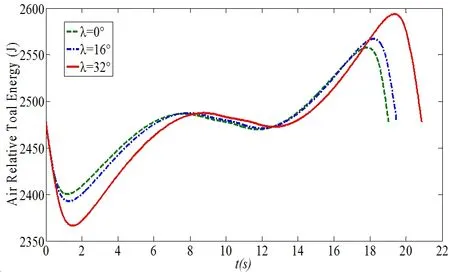
Figure 16:Air relative total energy for three cutting-in angles in a cycle of dynamic soaring.

In Fig.16,the air relative total energy variation trends are almost the same.At the initial of the soaring,the energy descends rapidly.With the increase of the flight altitude,the wind speed increases at the same time.So when the airspeed of the UAV increases,and the UAV’s air relative total energy increases.During 8～14 seconds,there is a slightly decrease of energy,which means that,during the turning in the high altitude,it’s balanced between income and expenditure of air relative total energy.And the bigger the cutting-in angle is,the less of energy’s limit varies.Of course,it can get the same conclusion from Eq.20.After the UAV starts to head down from 14 seconds,the air relative total energy increases sharply as the UAV gets pulled by the wind.However,as a consequence of lowCLand high CDduring the turning in low altitude,the air relative total energy of UAV decreases sharply at last.

So,in a cycle of dynamic soaring,the energy absorption of UAV mainly occurs in climbing with headwind and gliding with tailwind.In an optimal soaring trajectory,there is little energy loss in turning in high altitude,because it can select the suitable turning radius R and attitude angles to reduce the energy loss.From Eq.36,a suitable φ can make the energy loss in an optimum value.

4 Conclusions

Dynamic soaring enables UAV to obtain energy from the flying environment,and to prolong its endurance.This paper examines the scope of cutting-in angle in several aspects.During the process of calculating,the gradient wind’s direction is taken into decomposition.Accordingly,the cutting-in angle is solved by means of balance between energy gain and loss.An optimal control problem is formulated to determine the optimization of dynamic soaring of the UAV,through which the final energy is ensured to approximately equal to the initial energy after a cycle of dynamic soaring.By means of theoretical analysis and modeling simulation,the following conclusions can be summarized:

•In the special scale of cutting-in angle,the UAV can absorb enough energy from the wind field by the means of dynamic soaring.With the increasing of the cutting-in angle,the energy gain/loss is increased at the same time,while the energy gain is equal to the energy loss in the optimal trajectory.When the cutting-in angle exceeds the maximum value,the energy gain from the environment cannot support the energy loss,which means that the UAV cannot accomplish a dynamic soaring cycle in the wind field without propulsive thrust.

•In the dynamic soaring,the energy-extraction mainly occurs in climbing with headwind and glider with tailwind.During the turning at high altitude,the air related to total energy of UAV keeps stationary.The energy loss mainly occurs at turning in low altitude.When the UAV reaches the peak altitude,UAV’s airspeed reaches the minimum value.In order to make sure that the UAV still has enough lift for flight during the turning at the high altitude,the lift coefficient needs to reach the maximum value.

The methods and conclusions are very useful to instruct UAV to fly in the gradient wind field without thrust.For practical applications an important source is not only theoretical investigation but also experimental verification.Furthermore,the more accurate flight model with 6 DOF would be useful to investigate dynamic soaring flight,and some dynamic soaring experiments would also be important for further investigations.

Bencate,R.;Sousa,J.(2011):Shear Wind Estimation.AIAA Guidance,Navigation,and Control Conference,pp.1-8.

Bonnin,V.;Toomer,C.C.(2013):Energy-Harvesting Mechanisms for UAV Flight by Dynamic Soaring.AIAA Atmospheric Flight Mechanics(AFM)Conference,pp.1-16.

Bower,G.C.(2011):Boundary Layer Dynamic Soaring for Autonomous Aircraft:Design and Validation.Phd thesis,Stanford University,Stanford.

Chakrabarty,A.;Langelaan,J.W.(2010):Flight Path Planning for UAV Atmospheric Energy Harvesting Using Heuristic Search.AIAA Guidance,Navigation,and Control Conference,pp.1-18.

Clarence,J.D.C.(1964):A Mathematical Analysis of the Dynamic Soaring Flight of the Albatross with Ecological Interpretations.Virginia Institute of Marine Science.

Deittert,M.;Richards,A.;Toomer,C.A.(2009):Engineless Unmanned Aerial Vehicle Propulsion by Dynamic Soaring.Journal of Guidance,Control and Dynamics,vol.32,no.5,pp.1446-1457.

Denny,M.(2009):Dynamic soaring:aerodynamics for albatrosses.European Journal of Physics,vol.30,pp.75-84.

Langelaan,J.W.;Spletzer,J.;Montella,C.(2012):Wind field estimation for autonomous dynamic soaring.2012 IEEE International Conference on Robotics and Automation,pp.16-22.

Lawrance,N.R.J.;Sukkarieh,S.(2011a):Autonomous Exploration of a Wind Field with a Gliding Aircraft.Journal of Guidance,Control and Dynamics,vol.34,pp.719-723.

Lawrance,N.R.J.(2011b):Path Planning for Autonomous Soaring Flight in Dynamic Wind Fields.2011 IEEE International Conference on Robotics and Automation,pp.2499-2505.

Lawrance,N.R.J.;Sukkarieh,S.(2009):A guidance and control strategy for dynamic soaring with a gliding UAV.2009 IEEE international Conference on Robotics and Automation,pp.3632-3637.

Lawrance,N.R.J.(2011c):Autonomous Soaring Flight for Unmanned Aerial Vehicles.Phd thesis,The University of Sydney,Sydney.

Rayleigh,J.W.S.(1883):The soaring of Birds.Nature,vol.27,pp.534-535.

Richardson,P.L.(2010):How do albatrosses fly around the world without flapping their wings?Progress in Oceanography,vol.88,pp.46-58.

Sachs,G.;Lesch,K.;Knoll,A.(1989):Optimal Control for Maximum Energy Extraction from Wind Shear.AIAA Guidance,Navigation and Control Conference,pp.556-561.

Sachs,G.;Traugott,J.;Nesterova,A.P.(2012):Flying at No Mechanical Energy Cost:Disclosing the Secret of Wandering Albatrosses.PLOS ONE 7,pp.1-11.

Stephen,A.C.;Kenheth,J.K.;Peter,P.;Linton,W.(2005):Unmanned Aircraft Systems Roadmap 2005-2030.United States Department of Defense,pp.138.

Sukumar,P.P.;Selig,M.S.(2010):Dynamic Soaring of Sailplanes over Open Fields.28th AIAA Applied Aerodynamics Conference,pp.1420-1430.

Traugott,J.;Holzapfel,F.;Sachs,G.(2010):Conceptual Approach for Precise Relative Positioning with Miniaturized GPS Loggers and Experimental Results.RTO-EN-SET-116,pp.4-24.

Zhao,Y.J.;Qi,Y.C.(2004):Minimum fuel powered dynamic soaring of unmanned aerial vehicles utilizing wind gradients.Optimal Control Application and Methods,vol.25,no.5,pp.211-233.

Zuo,Z.Y.(2013):Adaptive trajectory tracking control design with command filtered compensation for a quadrotor.Journal of Vibration and Control,vol.19,pp.94-108.

1College of Aerospace Sciences and Engineering,National University of Defense Technology,Changsha,Hunan,410073,China.

2Corresponding author.Tel:+8613548776007;Fax:+86-0731-84573189;E-mail:jackerzhu@163.com