利用重力数据和深度控制同时估算三维基底深度和密度差

刘富强

（新疆维吾尔自治区有色地质勘查局物探队乌鲁木齐830011）

利用重力数据和深度控制同时估算三维基底深度和密度差

刘富强

（新疆维吾尔自治区有色地质勘查局物探队乌鲁木齐830011）

本文提出了一种重力反演方法，它结合一些已知的基底深度，同时估算了沉积盆地的三维基底起伏和沉积包裹体的密度差随深度按抛物线衰减的参数。沉积物被并列在水平方向的三维垂向棱柱体网格所近似。棱柱体的厚度代表基底的深度，它是从重力数据中被估算的参数。为了估算密度差随深度抛物线衰减的参数，并得到稳定的基底深度的估算，我们对基底深度强行平滑并近似钻孔的估计深度和已知深度。将该方法应用于复杂的两个沉积截面的三维基底起伏的组合数据中，能清楚地用抛物线定律描述密度差随深度的变化。它的结果良好的估算密度差随深度抛物线衰减和基底起伏的真实参数。

重力数据深度控制三维基底深度密度差

1 引言

大多数的重力反演方法估算沉积盆地的基底起伏可以划分为两类：第一类假定在沉积层和基底之间的一个密度差是常量（Bott,1960;Oldenburg, 1974;Leãoetal.,1996;Barbosaetal.,1997）；第二类是假定由压实引起的沉积物的密度差随深度变化。一些基底深度的重力数据反演的新发展假定密度差随深度是单调衰减的，如指数定律（Cordell,1973），二次方程定律（Rao,1990;Gallardo-Delgado,2003），抛物线定律（_Chakravarthi和Sundararajan,2004），三次多项式定律（García-Abdeslem,2005）和双曲线定律（Silvaetal.,2006）。

用抛物线定律方法（如Chakravarthi和Sundararajan,2007）估计区域重力背景和沉积盆地的三维基底起伏深度，需假定密度差随深度衰减遵循抛物线定律。满足两个假设，一是假设各个重力观测站的重力异常是由重力观测站以下的密度差变化符合抛物线定律的水平无限平板产生的，这个初始假设半定量地遵循几何学基底起伏。二是假设：基底起伏很简单，基底的深度很浅，密度差随深度的衰减率很低。第一个假设在地质学角度上是很重要的；当结合第二个假设时，它会得到一个稳定的解。

通过假设密度差随深度衰减符合抛物线定律来提出一个三维基底深度重力反演。为了确定定义的密度差随深度抛物线衰减的参数，通过平滑基底深度和已知深度，估算一个稳定的基底起伏。重复这些步骤是为了得到这些参数的不同值，并选择那些与钻孔资料的基底起伏相关性较好的参数值。通过正则化参数的稳定函数最小化，使目标函数成为全局凸函数来获得基底深度的估算。结果表明，该方法不依赖于基底深度的初始值，并且可以用来估算那些地质构造复杂的基底起伏。

2 研究方法

假设一个由均匀基底岩石和不均匀沉积物所组成的沉积盆地，基底和沉积物之间的密度差随深度z减小符合抛物线定律（Raoetal.,1994）：

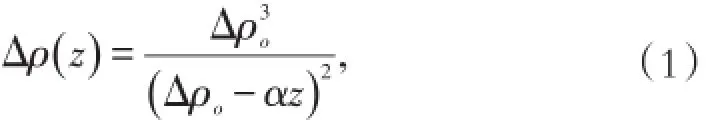
式中，Δρo是地表面的密度差；α是通过深度控制密度差梯度的因子。

假设一个均匀基底中分离出来的任意界面，为了估计该界面的起伏，在x-y空间选择一个包含盆地的整个上表面的有限区域，将它沿x和y方向离散成一个mx×my的三维垂向并列分布的棱柱体的网格（图1）。每个棱柱体的顶部与地表面一致，并且所有棱柱体沿x方向的大小为dx、沿y方向的大小为dy。M个棱柱体的厚度(M=mx·my)便是待估算的参数。棱柱体的厚度pj,j=1,…,M，代表在M个离散点沉积基底的深度，它与第i个观测点(x=xi,y=yi,z=zi)重力异常gi非线性相关

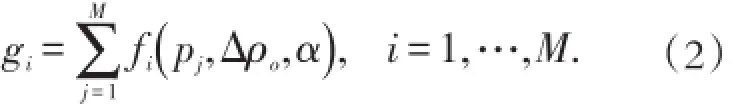
计算第i个观测点()xi,yi,zi的非线性函数

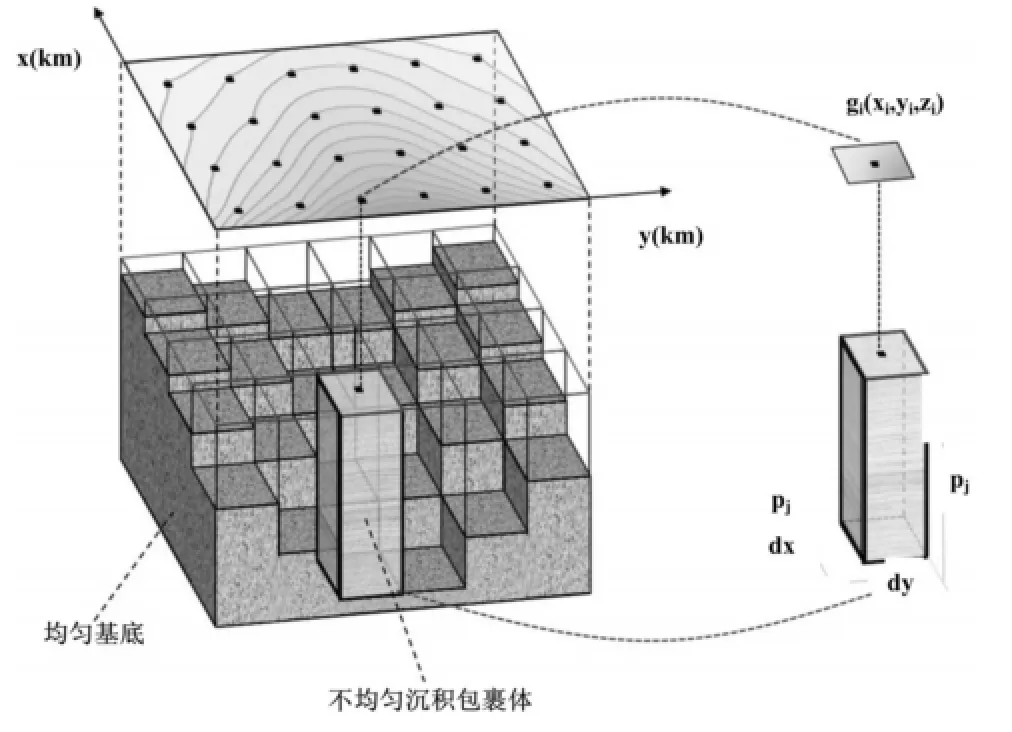
图1 解释模型

重力异常值（灰色轮廓线）是由下伏于沉积包裹体（图上未给出）的均匀基底构建的规则网格（黑点）插值得到的。包含沉积包裹体的次级界面是离散成厚度参数被估计的三维垂向棱柱体的网格。右边的插图展示了第j个三维棱柱体和第i个重力异常的垂向分量的坐标。

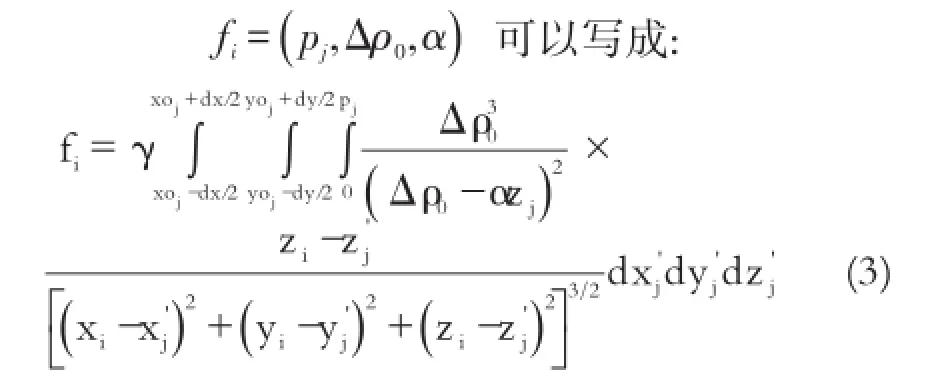
式中，γ是牛顿万有引力常数;xoj和yoj是第j个棱柱体中心的x,y坐标。

公式（3）即是Chakravarthietal.（2002）介绍的积分方程的封闭形式。

假设重力数据是规则网格（图1）插值得到的，它的每个观测点的x,y坐标与每个棱柱体中心的水平坐标相一致。定义gi为矢量g→≡() g1,…,gMT的第i个分量（T代表转置），它包含了由M个棱柱体模拟的包裹体密度差随深度按方程（1）衰减所引起的理论重力异常。

2.1 基底深度反演

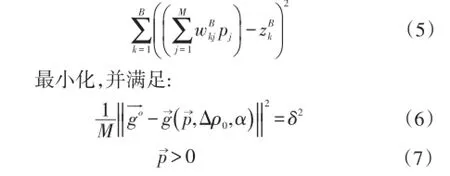
在方程（6）中Δρ0和α会在下一节通过一些步骤的叙述而获得。一阶Tikhonov正则化函数式（4）TikhonovandArsenin,1977）利用平滑来约束基底起伏。该函数式中，‖‖·是欧几里得范数，R→是一个矩阵代表一阶离散的微分算子（Twomey,1963;Vogel, 2002）。

表达式（5）中的函数式介绍了水平坐标上使已知深度和估计深度接近的基底深度的钻孔信息。该函数式中，B是贯穿基底起伏面深度zBk,k=1,…,B的钻孔个数，wBkj是B×M阶矩阵WB的第kj个元素，该矩阵的行只包含一个非零元素，相当于一个单位元素。这个非零元素位于WB的第k行，与矢量p→的元素有关系，其相应的水平坐标是最接近第k个钻孔的水平坐标。在拟合程度较差的函数式（6）中，是N维矢量的第i个元素包含了第i个观测点（2）上计算的重力异常，δ2是重力数据中的干扰识别的均方差期望。

带约束的反问题由函数式（4）和（5）的极小值给出，方程（6）给出了满足的约束条件，可以改写成非约束函数式的极小值的最优化问题:

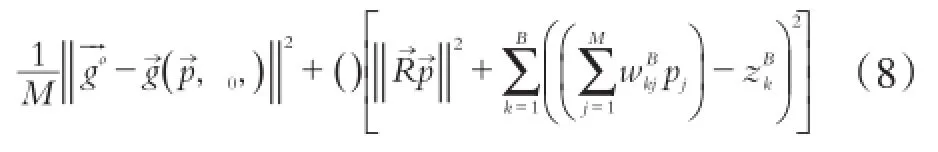
其中，μ(δ)是控制拟合程度的函数式（8）和先验条件（4)和(5）之间权重衡量的非负标量。函数式（8）的最小值通过Marquardt（1963）的方法获得，在每次迭代中加入海森矩阵的高斯-牛顿近似值（Silvaetal., 2001）。最后，非负性约束（方程7）由一个同胚变换给出（例如Barbosaetal.,1999）。然而，这些约束也能由Haskell和Hanson（1981）提出的通过非负性约束最小二乘算法给出（SilvaDiasetal.2007）。

2.2 估算Δρ0和α

为了估算基底起伏（即为了获得由方程8给出的非约束问题的最小值），我们第一步需要获得表面的密度差Δρ*0和密度差随深度抛物线衰减的因子α*（方程1）的估计值。在下文中会得到一对的值。给定这对Δρ0和α的值，并且获得一个估计矢量参数，使满足重力观测值在测量误差（6）和非负性约束（7）以内的一阶Tikhonov稳定函数式（4）最小化。估算矢量∧p(Δρ0,α)之后，来求方程的值:

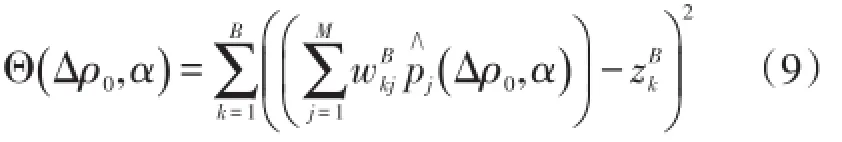
接下来，把Θ()Δρ0，α画到平面Δρ0×α上。重复这个过程，该过程是由解释者设定的对不同点的一对() Δρ0，α产生一对增量为Δρ0和Δα的离散图形Θ()Δρ0，α的最小() Δρ0，α。该离散图形允许一个Θ()0,α*的视觉估计。然后，检查下面的不等式是否成立：Δρ*0,α*是观测值满足已知L的极限的最优值；否则，离散区域Δρ0×α可能不能得到真实的一对()

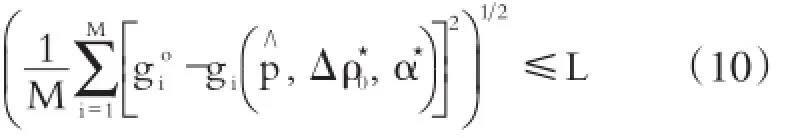
如果满足上式，那么估算值p∧() Δρ*0,α*，既然这样，那么离散化的网格是被精细化的且上述过程是被反复的。Δρ*

3 组合模型的应用

图2a给出了由模拟沉积盆地的复杂基底起伏（图2b）产生的噪声-干扰布格异常（蓝色实线）。在有26×78个节点的x和y方向（分别代表北南和东西向）网格间距为1km的网格上，重力数据是在其z= 0km平面上计算出的。用标准偏差为0.1mGal的均值为零的高斯伪噪声干扰理论异常。

图2b给出了等高线图和基底起伏的实际深度的透视图。假设一个非均匀沉积包裹体覆盖在均匀的基底上，该基底有一个复杂的结构骨架被由北西走向的正断层将基底起伏面分割成复杂的镶嵌构造凹陷和凸起的两个区域强有力地控制着（如图2a和b，Ⅰ和Ⅱ）。假设密度差随深度衰减符合抛物线定律（方程1）。我们定义区域Ⅰ和Ⅱ密度变化随深度的不同抛物线由每个区域的不同对点()Δρ0，α赋值（区域Ⅰ为-0.6g/cm3和0.10g/cm3/km，区域Ⅱ为-0.4g/cm3和0.05g/cm3/km）。区域Ⅱ是西北狭长的次级盆地包含两个独立的、最大深度达到7.2km的断层边界构造凹陷。区域Ⅰ中，有一系列邻近的交替出现的构造凹陷和构造凸起被西北走向的断层控制。这一区域的深度范围为3.5到7.2km。图2a最突出的特点是，无论是区域Ⅱ存在的两个构造凹陷还是区域Ⅰ存在的四个构造凹陷，都不能很容易的从重力异常检查区中推断出。

3.1 估算Δρ0和α

为了估算三维基底起伏，需要通过图2中每个区域Ⅰ和Ⅱ离散的Θ() Δρ0，α的图形（9）知道最合适的一对() Δρ0，α的估计值。我们建立一个初始的解释模型，它由三维垂向分布的棱柱体在x、y方向各自有相同的1.0km的网格间距的26×78的网格组成。然后，我们定义调查间隔和在区域Ⅰ和Ⅱ中Δρ0与α的增量从而产生函数式Θ()Δρ0，α（9）的离散图形，见图2a；对于区域Ⅰ，我们用到了三个钻孔（图2a中的黑色星号）的基底面深度的信息。

我们注意到一个宽的最小值的区域（图2a中的黑灰色区域）包含实际的一对() Δρ0，α的值（图2a中的白色十字）。所有位于最小值区域里成对的() Δρ0，α的值与实际基底起伏好的估算值有关系，就像插图中四个基底起伏（图2b中的灰色虚线）的估计，分别是由在1～4点（图2a中的白点和白色十字）上用成对的() Δρ0，α的值得到的。这些成对的值服从可接受的异常拟合（平均误差≈0.08mGal）。

这些结果表明函数式Θ()Δρ0，α（9）的最小值区域可能不包括实际的()Δρ0，α的值。它依赖于钻孔的数量和分布以及对重力的响应。

3.2 估算三维基底起伏

图2c给出了估算基底起伏深度的等高线图和透视图，它用Δρ0和α的估计值估计基底起伏的深度，Δρ0和α是由区域Ⅰ和Ⅱ履行的一个系统搜索函数式Θ() Δρ0，α得到的，并检查是否满足不等式(10)，它定义了一个可能的不确定区域。在Θ() Δρ0，α的最小区域中运用成对（Δρ*0=-0.6g/cm3,α*=0.10g/cm3/km）值，它符合数据约0.08mGal的平均误差。将基底深度估计和实际深度对比，我们证明我们的方法在恢复复杂基底起伏时有很好的效果。

该方法可以改进呈现不连续起伏的基底的沉积盆地的基底估计，例如Barbosaetal（1999）提出的方法。该方法也可以在比沉积盆地更小规模的类似盆地特征中应用，例如（Silvaetal.,2009）废弃的填埋区。

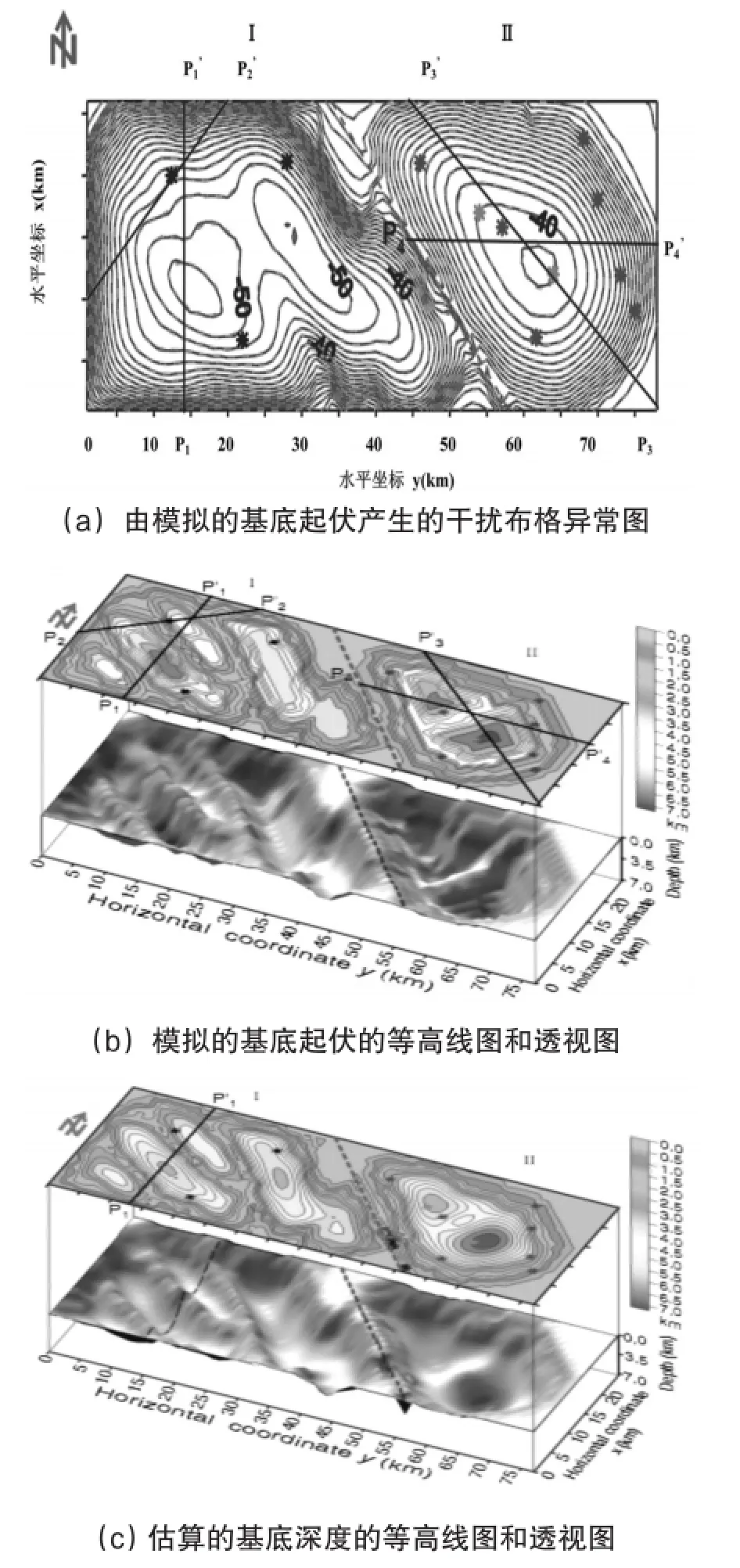
图2 组合测试

4 结论

众所周知，仅仅用重力数据确定密度和场源值是不可能的，因此，利用很少点上的基底深度信息去同时估计三维基底起伏（场源值）和沉积盆地的密度差随深度抛物线衰减的参数。此外，在一些点上用场源体的信息去克服涉及场源体物理性质的不明确性。组合模型实例表明，即使在复杂的地质条件下，该方法也得到了良好的沉积基底起伏估计。

[1]CristianoM.Martins1,ValeriaC.F.Barbosa,andJo o B.C.Silva,Simultaneous3Ddepth-to-basementanddensitycontrastestimatesusinggravitydataanddepthcontrolatfew points.GEOPHYSICS,VOL.75,NO.3,2010;P121-128.

[2]Barbosa,V.C.F.,P.T.L.Menezes,andJ.B.C.Silva, 2007,Gravitydataasatoolfordetectingfaults:In-depthenhancementofsubtleAlmada’sbasementfaults,Brazil:Geophysics,72,no.3,B59-B68.

[3]Barbosa,V.C.F.,J.B.C.Silva,andW.E.Medeiros, 1997,Gravityinversionofbasementreliefusingapproximate equalityconstraintsondepths:Geophysics,62,1745-1757.

[4]Beltrao,J.F.,J.B.C.Silva,andJ.C.Costa,1991,Robustpolynomialfittingforregionalgravityestimation:Geophysics, 56,80-89.

[5]Chakravarthi,V.,H.M.Raghuram,andS.B.Singh,2002, 3Dforwardgravitymodelingofdensityinterfacesabovewhichthe densitycontrastvariescontinuouslywithdepth:Computersand Geosciences,28,53-57.

[6]Gallardo-Delgado,L.A.,M.A.Perez-Flores,andE.Gomez-Trevino,2003,Aversatilealgorithmforjoint3Dinversionof gravityandmagneticdata:Geophysics,68,949-959.

[7]Garcia-Abdeslem,J.,2005,Thegravitationalattraction ofarightrectangularprismwithdensityvaryingwithdepthfollowingacubicpolynomial:Geophysics,70,no.6,J39-J42.

[8]Leao,J.W.D.,P.T.L.Menezes,J.F.Beltrao,andJ.B.C. Silva,1996,Gravityinversionofbasementreliefconstrainedby theknowledgeofdepthatisolatedpoints:Geophysics,61,1702-1714.

收稿：2014-12-24

10.16206/j.cnki.65-1136/tg.2015.04.007