GIS辅助下滑坡灾害危险性区划图的绘制——以四川省攀枝花市为例
2015-12-12王喜娜黄华兵
王喜娜,黄华兵,班 亚,李 杰
(1.武汉大学测绘学院,湖北武汉430079;2.中山大学地理科学与规划学院,广东 广州510275)
一、引 言
滑坡是指构成斜坡的岩土体在重力作用下失稳,沿着坡体内部软弱结构面(带)发生剪切而产生的整体性运动现象,俗称垮山、地滑,是较为严重的一种山地灾害。滑坡灾害是我国山区最重要的自然灾害之一,往往给人类社会和自然环境带来巨大的伤害和损失。因此加强滑坡灾害危险性评估研究,以及进行滑坡灾害的危险性区划制图对于提高应对滑坡灾害的防灾减灾能力具有重要的基础意义[1]。
攀枝花地处四川省西南部,川滇交界处,界内山区面积占总面积的88.38%,地貌类型复杂多样,且是全国有名的矿区,因此加强地质灾害防范,做好地质灾害普查和危险性区划制图是地区国土部门的重要基础工作。
基于地理信息系统的滑坡危险性区划制图是识别和管理潜在滑坡风险的有效工具。地理信息系统具有强大的地理信息存储、处理、分析和展示功能。近20年,地理学家和工程技术人员运用GIS识别滑坡,绘制滑坡灾害区划图,他们采用了多种方法,如综合参数法(专家打分法、层次分析法)[1-3]、信息量法[4-5]、模糊综合评判法[6]、神经网络法[7]、Logistical回归模型[8]等方法。
笔者基于GIS技术和逻辑回归方法,以四川省攀枝花市为研究区域,选取高程、坡度、坡向、土地利用类型、地层岩性、道路交通、河流水系7个影响因子作为评价指标,建立逻辑回归模型进行预测,编制了滑坡危险性区划分布图,圈定了滑坡灾害多发、易发区域。模型结果的预测情况显示与实际滑坡灾害点在空间上的分布十分吻合。
二、研究区域概况
四川省攀枝花市位于 26°05'N—27°21'N,101°08'E—102°15'E,包括东区、西区、仁和区、米易县、盐边县5个区县,研究区总面积7 440 km2,最高海拔4 195.5 m,最低海拔937 m。攀枝花市地处攀西裂谷中南段,属浸蚀、剥蚀中山丘陵、山原峡谷地貌,山高谷深,盆地交错分布,地貌类型复杂多样。该区域地质灾害频发,截至2010年,研究区内共发现滑坡灾害点及滑坡灾害隐患点184处,具体分布如图1所示。
攀枝花市的滑坡数量多,分布广,规模大,而且发生的频率和成灾的概率都大,给该区的工农业生产﹑交通运输和人民生命财产造成了很大的危害。因此,加强地质灾害防范是当地安全管理工作的重中之重。
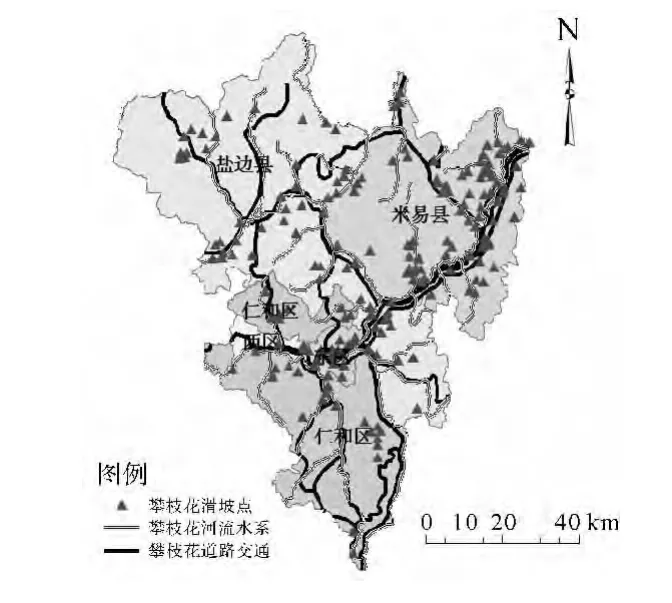
图1 滑坡灾害分布图
三、研究方法
1.影响因子的选择
滑坡灾害的发育形成受内外力综合影响,本文根据攀枝花地区的地质、地形调查资料,综合考虑滑坡内外动力影响因素进行滑坡影响因子的选择。内动力因素包括地质因素、地形因素的和水文因素,其中地质因素用岩性来衡量,地形因素用坡度、坡向与高程来表达,水文因素用距水流距离来衡量。外动力因素包括人工开挖、修坡建房等人类工程活动,可利用距公路距离和土地利用类型来表达人类活动对滑坡的影响。综合上述考虑,选取地层岩性、坡度、坡向、高程、距水流距离、距公路距离和土地利用类型共7个滑坡影响因子进行滑坡危险性评价。
2.数据来源
研究数据来源于中国山地灾害与环境数据库,由中国科学院水利部成都山地灾害与环境研究所提供。原始数据包括攀枝花市1∶25万行政界线数据、攀枝花市1∶25万栅格地形图数据(DEM)、攀枝花市1∶50万地质类型数据、攀枝花市1∶10万土地利用数据(2010年)、攀枝花市1∶10万河流水系湖泊分布数据、攀枝花市遥感影像数据、攀枝花市道路交通数据、攀枝花市历史滑坡灾害及灾害隐患点分布数据等。
3.数据预处理
首先将数据转换到统一的地理坐标系和投影坐标系下;然后将土地利用类型和地质岩性分布两个矢量图层栅格化,生成的栅格图像的分辨率与数字高程模型(DEM)的分辨率一致,即85 m×85 m;由河流线图层和道路线图层生成距离栅格图,由DEM生成坡度栅格图和坡向栅格图;最后将所有栅格图叠加,将发生滑坡的184个样本点和未发生滑坡的148个样本点共332个点作为采样点,提取7个影响因子的属性数据,编制 Logistic回归数据表。图2—图8为各影响因子专题图。
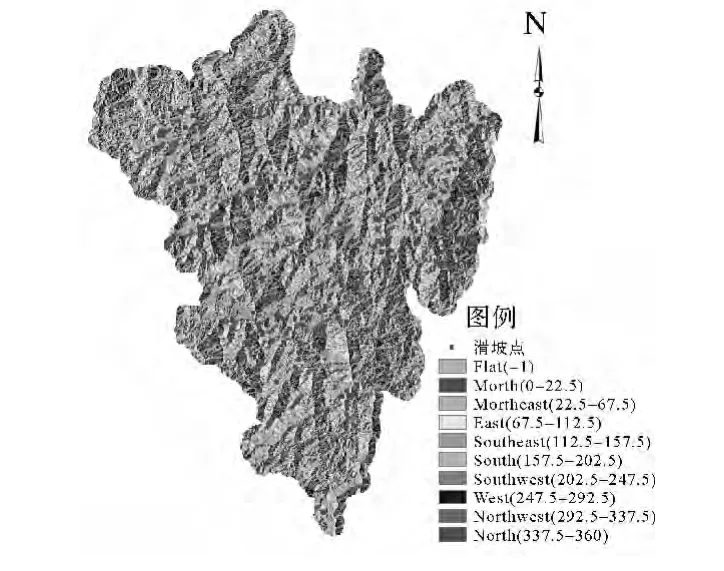
图2 坡向专题图
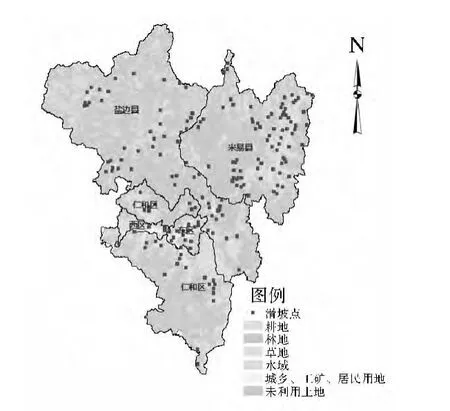
图3 土地利用专题图
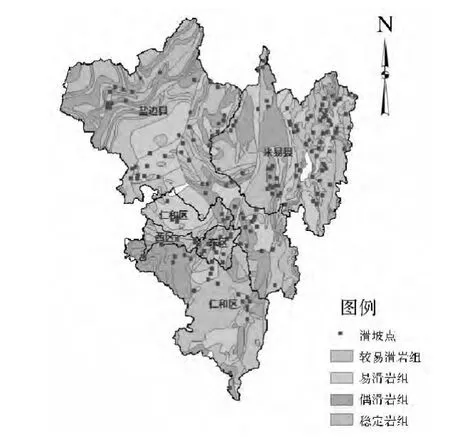
图4 地层岩性专题图
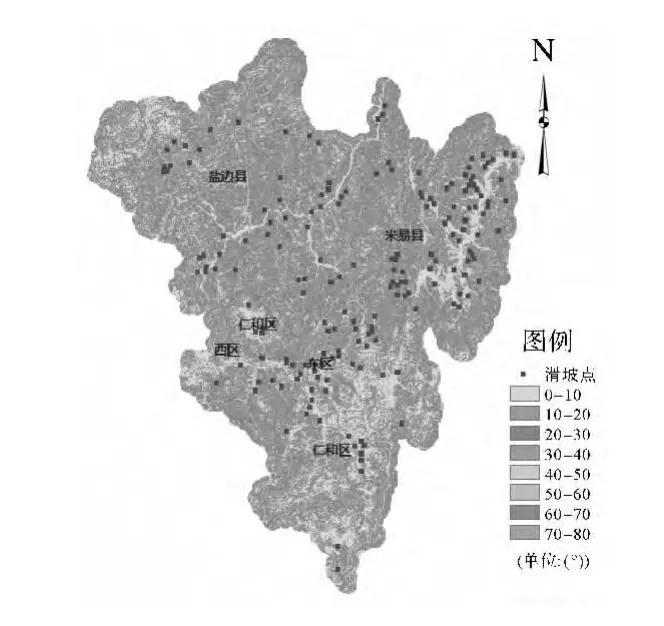
图5 坡度专题图
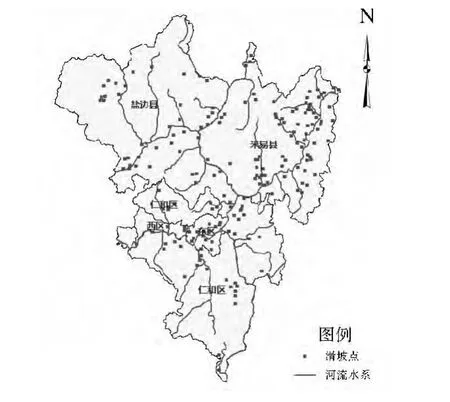
图6 水系专题图
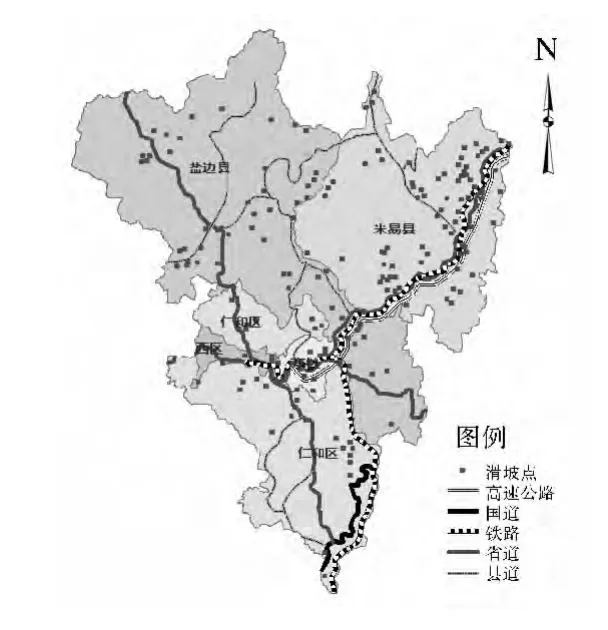
图7 道路交通专题图
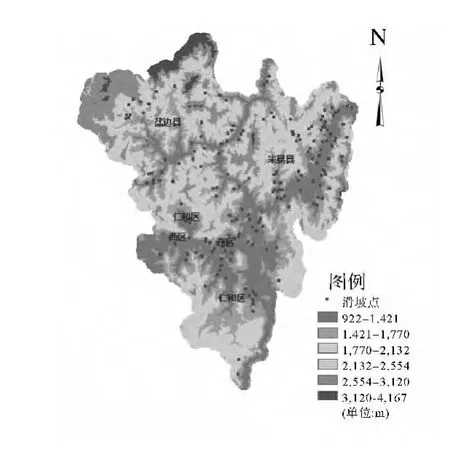
图8 数字高程模型
4.危险性评价模型
(1)理论依据
滑坡危险性评价的理论依据是工程地质类比法,即类似的工程地质环境及其组合可能发生类似的滑坡作用。滑坡灾害危险性评价模型经历了从定性模型、半定量模型到定量模型的发展。定性模型是基于专家的野外现场经验判断,直接从现场调查得出的易发性和危险性结果;半定量模型虽然使用数值方法对地质目标的空间位置和属性开展数值计算,并得到了量值,但评价因素权重确定仍依赖于专家经验;定量模型是根据过去区域滑坡灾害的分布情况,在数理统计理论的指导下,建立影响因素和地质灾害之间的数学模型,在模型得到验证后,将其应用到地质环境相同或类似的区域,以评价地质灾害的发生情况。定量模型包括二元与多元回归模型、人工神经网络模型、分形理论模型、支持向量机等。逻辑回归分析方法没有关于分布类型、协方差阵等方面的严格假设,不要求数据的正态分布,其参数估计比多元判别分析更加稳健,因此逻辑回归方法在滑坡危险性评价中有着更为广泛的应用。本文即选用逻辑回归模型建立预测模型。
(2)逻辑回归模型
逻辑回归模型用于研究某一随机事件发生的概率与某些因素之间的关系,如滑坡发生的概率与地层岩性、高程、河流水系分布等的关系。在逻辑回归分析中,因变量Y是一个二分类变量,其取值Y=1和Y=0分别表示滑坡的发生和不发生。假定有p-1个因素 X1,X2,…,Xp-1影响 Y 的取值,π =P{ Y =1}为研究对象,以π(x)表示滑坡发生的概率,建立 π 与 X1,X2,…,Xp-1的 Logistic 模型
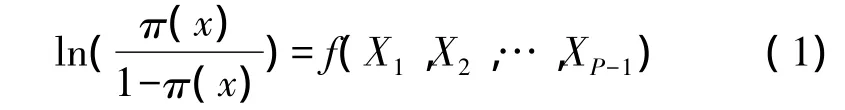
式中,f(X1,X2,…,XP-1)取为 X1,X2,…,Xp-1的线性函数,即
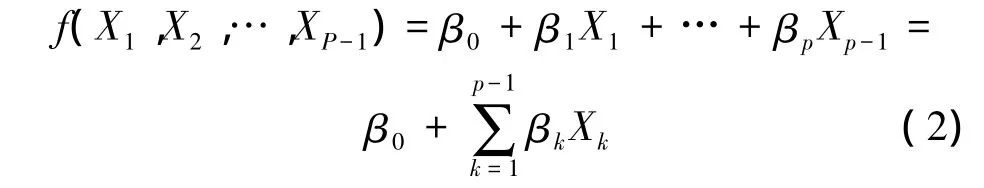
此时
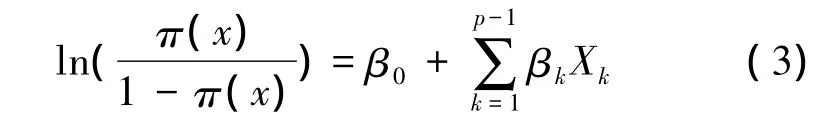
即最终的逻辑回归模型为
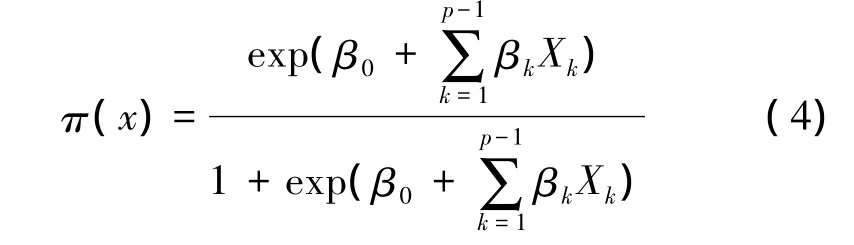
式中,β0代表回归常数;βk代表第k个影响因素的回归系数(k=1,2,…,p-1)。
在高程、坡度、坡向、土地利用类型、地层岩性、距河流距离、距公路距离7个影响因子中,DEM、坡度图、距河流距离图和距道路距离图的栅格值都属于连续变量,在预测时需要对连续变量进行合理的状态划分,这样对优化预测模型,提高预测效果有一定的作用。划分区间的原则是区间之间的数据要有尽可能大的差异性,但区间数不宜太多。根据快速聚类方法划分的影响因子分类分级,见表1。
本文选取了184个滑坡灾害点(含隐患点)和148个未发生滑坡的地点作为样本,共计332个样本点,使用ArcGIS中Spatial Analyst工具箱Extraction工具中的Sample功能,提取样本点上的各个影响因素属性,作为试验数据,带入SPSS中进行二元逻辑回归计算。
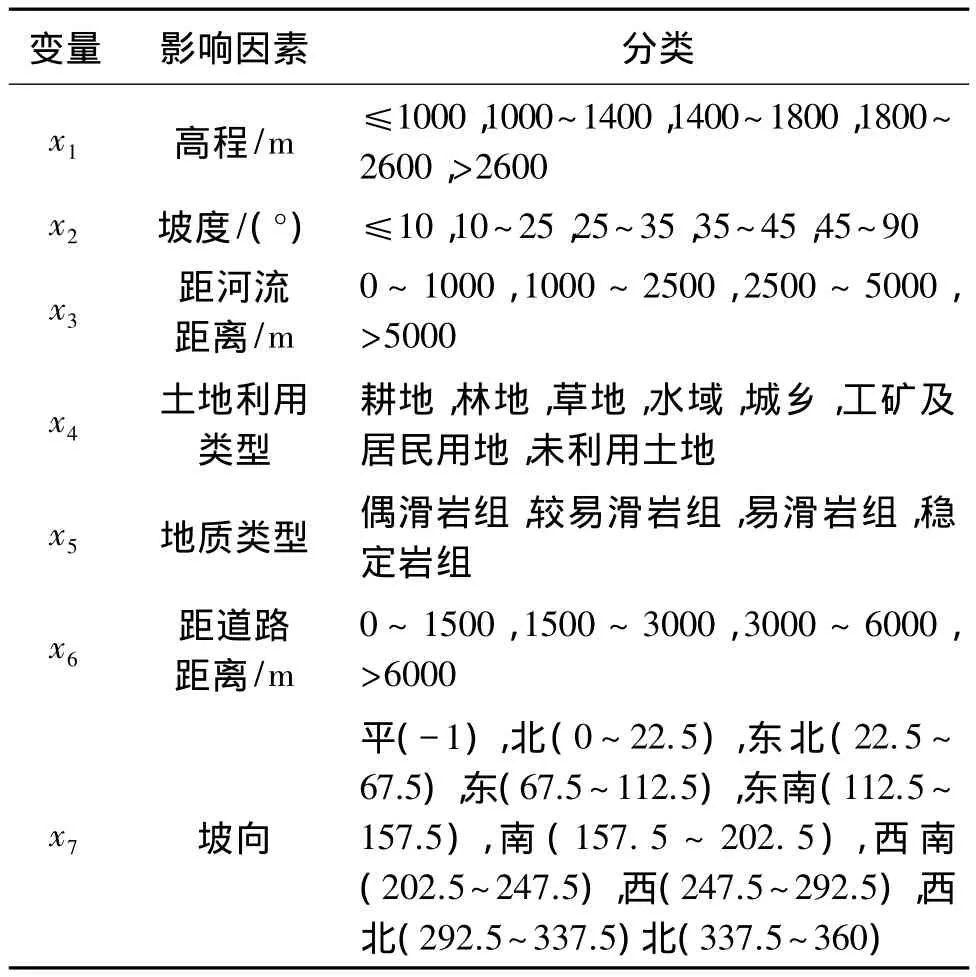
表1 影响因子分类分级表
5.计算结果及分析
由SPSS的逻辑回归过程,首先得到似然比统计量K2的观测值K2=68.753,自由度为7,检验的p值为p=p{χ2(7)>68.753}≤0.000 1。由此可见,x1,x2,…,x7对概率 P{ Y =1}的综合影响是高度显著的,建立的逻辑回归模型是有意义的,即投入的自变量中,至少有一个自变量能有效预测因变量反映的事件发生的概率。各个影响因素的参数估计结果见表2。
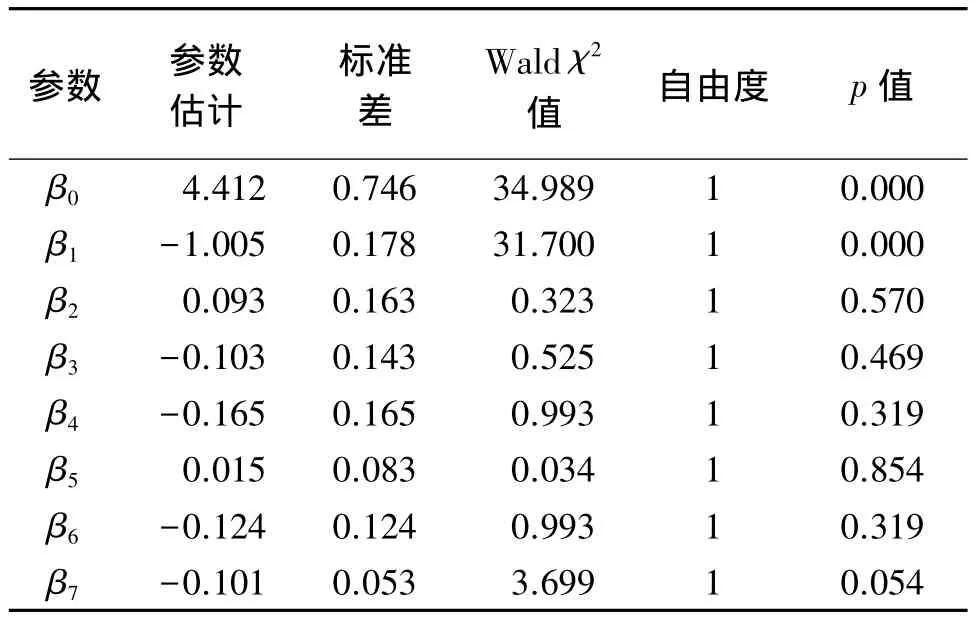
表2 参数估计值及统计检验
由于 β2、β3、β4、β5、β6的 Wald 检验的 p 值较大,因此 β2、β3、β4、β5、β6对 P Y=1{ }的影响不显著,为了建立一个更紧凑有效的Logistic回归方程,最终只保留x1、x7两个自变量,得到如下的Logistic回归方程

式中,x1代表高程因素;x7代表坡向因素。方程表明,攀枝花地区滑坡的发生受高程因素和坡向因素影响较大,这两个因素对滑坡发生有较好的解释效果。
由式(5)计算各个栅格单元的逻辑回归预测值,并根据概率大小将回归预测值划分为5个等级,见表3。
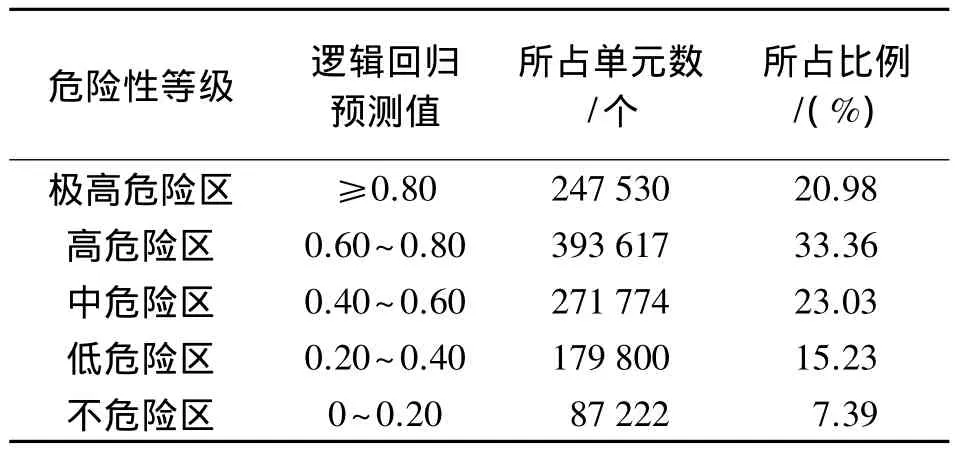
表3 危险性等级划分
编制的攀枝花市滑坡灾害危险性区划图如图9所示,历史滑坡点的频数分布如图10所示。由图9可以看出,攀枝花境内低、中、高和极高危险性分级区域面积占总面积的比例分别为15.2%、23.03%、33.36%和20.98%,说明攀枝花市约1/3地区属于中、低等地质灾害危险区,1/2以上地区属于地质灾害高和极高危险区。

图9 攀枝花地区滑坡危险性区划图
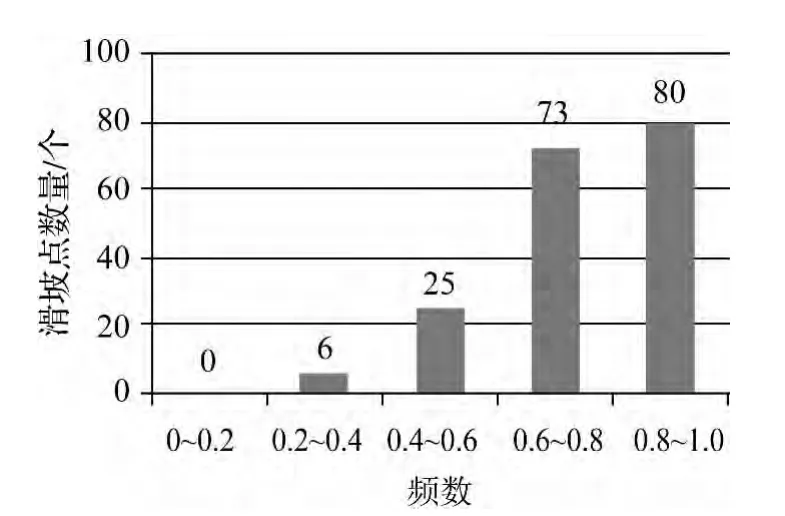
图10 历史滑坡点的频数分布
根据图9和图10的区划结果统计,危险性级别越高的区域,滑坡面积占分级区域面积的比例就越高,即滑坡灾害密度越大。高危险区和极高危险区集中了大量的滑坡灾害,而低危险区和中等危险区的滑坡分布相对稀疏。这说明本文划分的危险性级别区域符合历史滑坡分布现状,编制的攀枝花市滑坡危险性区划图合理、有效。
四、结束语
本文基于GIS技术,利用攀枝花市基础地理数据构建了滑坡灾害危险性评价指标体系和评价模型,定量、客观地完成了攀枝花市滑坡灾害危险性评估和区划,能够较好地反映滑坡灾害危险性的空间分布特征。
本研究得出的危险性没有时间因素,如果在此评价基础上叠加对滑坡危险性产生影响的时间因素,如地震因素或降雨因素,并以概率的形式与本文得到的危险性相乘,则可得到更为完整的滑坡危险性评价结果,也将会进一步提高评价精度。
[1]赵宝云,胡艳香,赵忠营,等.降雨诱发公路滑坡灾害危险性评价动态权重系统[J].地球与环境,2011,39(3):376-381.
[2]肖拥军,高华喜.库区移民新城滑坡灾害危险性区划研究[J].地球与环境,2011,39(3):388-392.
[3]童祥.基于ANP的铁路隧道塌方风险评价研究[J].隧道地下工程,2011(7):74-77.
[4]孟令超,卢晓仓,史晨晓,等.基于信息量模型的达曲库区滑坡危险性分析[J].灾害学,2009,24(4):31-34.
[5]朱良峰,吴信才,殷坤龙,等.基于信息量模型的中国滑坡灾害风险区划研究[J].地球科学与环境学报,2004.26(3):52-56.
[6]黄俊宝.基于GIS的地质灾害危险性模糊数学评判[J].福建地质,2009,28(4):346-351.
[7]刘艺梁,殷坤龙,刘斌.逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J].水文地质工程地质,2010,37(5):92-96.
[8]王卫东,陈燕平,钟晟.应用CF和Logistic回归模型编制滑坡危险性区划图[J].中南大学学报:自然科学版,2009,40(4):1127-1132.
[9]石菊松,张永双,董诚,等.基于GIS技术的巴东新城区滑坡灾害危险性区划[J].地球学报,2005,26(3):275-282.
[10]殷坤龙,张桂荣,陈丽霞,等.滑坡灾害风险分析[M].北京:科学出版社,2010:30,86-88.
[11]牛全福.基于GIS的地质灾害风险评估方法研究[D].兰州:兰州大学,2011.
[12]刑秋菊,赵纯勇,高克昌,等.基于GIS的滑坡危险性逻辑回归评价研究[J].地理与地理信息科学,2004,20(3):49-51.
[13]夏瑞庚,朱元友,李新平.基于神经网络的岩质边坡稳定性评估系统研究[J].自然灾害学报,1996(1):98-104.
[14]范金城,梅长林.数据分析[M].北京:科学出版社,2002.
[15]刘斌,殷坤龙,刘艺梁.基于栅格数据的巴东新城区滑坡空间预测[J].地质科技情报,2010,29(3):133-138.
