基于信息增益的传感器搜索调度模型对比分析

通讯作者，Email：zhangghui1230@163.com（衡阳师范学院数学与计算科学系， 中国 衡阳421002）

摘要针对目标搜索传感器调度问题，归纳总结了基于Shannon熵、KullbackLeibler熵和Rényi熵3种信息测度以及全局和局部两种信息增益，衍生出6种基于信息增益的搜索调度模型.通过数值仿真计算对比分析6种基于信息增益的搜索调度模型的目标捕获性能，结果表明基于3种信息测度的搜索调度模型对目标的捕获性能差别很小，而基于全局信息增益的搜索调度模型性能更优，仿真结果可为工程实践中传感器搜索调度方法的优选提供参考.

关键词搜索调度;熵;信息增益;累积捕获概率

中图分类号TN9111文献标识码A文章编号10002537（2015）06007805

Comparison of the Information Gain Based Sensor Search Scheduling Models

ZHANG  Guohui*

（Department of Mathematics and Computational Science， Hengyang Normal  University， Hengyang 421002， China）

AbstractTo deal with the problem of sensor search scheduling， three typical information measures based on Shannon entropy， KullbackLeibler entropy and Rényi entropy are summarized. Additionally， based on both of the  global information gain and local information gain， 6 kinds of search scheduling models are developed. The acquisition performance of all information based scheduling models are compared through simulation. The results indicate that， as for the three typical information measures， the acquisition performance of the search scheduling methods shows the same rules， while search scheduling model based on the global information gain shows better performance. The simulation results can be used as the reference for the search scheduling method in project.

Key wordssearch scheduling; entropy; information gain; cumulative acquisition probability

目标最优搜索理论起源于二战时期美国海军的反潜作战[1]，其动机是增强飞行员对上潜到水面充电的潜艇的检测能力.Koopman[2]对搜索论进行了系统的总结，给出最优搜索问题的3个基本元素：目标位置先验信息、搜索资源与检测概率之间的关系方程及搜索资源约束，并分别从运动学基础、目标检测及搜索资源最优配置角度对搜索理论进行了阐述.学者们针对目标最优搜索理论和相应的传感器搜索调度方法进行了大量研究，涉及雷达[2]、声纳[3]、可见光[4]、红外[5]、射电望远镜等主/被动探测设备，所建立的搜索调度模型包括累积发现概率模型[6]、信息增益模型[2]、自适应搜索模型[7]、分区搜索模型[8]等，这些研究成果已应用于许多不同的领域，如：水下目标或空间目标搜索、地面或海面搜救、地质勘探、信息分配、军事目标检测等.

Marcum [2]于1947年建立了累积发现概率模型，之后该模型被广泛应用于最优搜索，分别产生了最大化累积发现概率准则、最大化累积检测概率准则和最小化漏警概率准则，即在相同的时间和能量消耗下，使得传感器的累积发现（检测）概率最大化或使其累积漏警概率最小化.Keith[2]最早将信息论引入搜索调度领域，针对雷达搜索目标问题，提出最大化分辨力增益准则.Mark[910]针对地雷目标检测问题，从不同角度建立了两种目标观测不确定模型，并基于Keith的分辨力增益最大化准则，提出相应的传感器搜索调度方法.Mark[10]、王博[11]分别从理论上证明了搜索单元数N=2和N∈Z+条件下两种无调度搜索方法（顺序搜索和随意搜索）的性能.

信息增益模型作为一种常用的传感器搜索调度模型，通常采用Shannon熵[2]、KullbackLeibler熵[9]和Rényi熵[12]等信息测度，以最大化信息增益准则确定传感器对各区域的搜索时序，从而达到快速捕获目标的目的，是目标搜索调度领域使用最广泛的方法.本文将针对各种基于信息增益的传感器搜索调度模型，通过数值仿真计算，对比分析各种模型的搜索性能，以期为目标最优搜索方法的研究提供参考.

湖南师范大学自然科学学报第38卷第6期张国辉：基于信息增益的传感器搜索调度模型对比分析1基于信息增益的传感器搜索调度模型

对于预先编排好的n个搜索区域，任意区域k，k=1，2，…，n的状态Hk为二元，即有目标或无目标，可表示为Hk=1、Hk=0.假定传感器也是二元观测，即“目标存在”或“目标不存在”，t时刻对第k个区域的观测结果记为zk（t），则zk（t）∈{0，1}，而检测概率pd，虚警概率pf分别为pd=P（zk=1|Hk=1）， pf=P（zk=1|Hk=0）.基于上述假定，传感器搜索目标本质上是二元观测问题.

在基于信息增益的传感器搜索调度模型框架下，3个典型的信息测度Shannon熵DShannon，KullbackLeibler熵DKL和Rényi熵DRenyi分别定义为

DShannon（pki（t+1），pki（t））=pki（t+1）·log（pki（t+1））+（1-pki（t+1））·

log（1-pki（t+1））-pki（t）·log（pki（t））-（1-pki（t））·log（1-pki（t））， （1）

DKL（pki（t+1），pki（t））=pki（t+1）·log（pki（t+1）pki（t））+（1-pki（t+1））·log（1-pki（t+1）1-pki（t）），（2）

DRenyi（pki（t+1），pki（t））=1α-1log [（pki（t+1））α（pki（t））1-α+（1-pki（t+1））α（1-pki（t））1-α]，（3）

式（1）～（3）中pki（t），pki（t+1）分别表示传感器第t次观测前后目标出现在第k个搜索区域内的概率，即截获概率[1315]，也称为搜索区域的先验和后验状态概率密度.pki（t+1）可由pki（t）和观测结果通过Bayesian公式得到[2]，即

pki（t+1）=P（Hk=1|zk（t+1））=P（zk（t+1）|Hk=1）P（Hk=1|zk（t））∑1j=0P（zk（t+1）|Hk=j）P（Hk=j|zk（t））.   （4）

当Hk，zk取不同值时，对于式（4）P（zk（t+1）|Hk）项有

P（zk=1|Hk=1）=pd，P（zk=0|Hk=1）=1-pd，

P（zk=1|Hk=0）=pf，P（zk=0|Hk=0）=1-pf.（5）

信息增益实际上是t时刻传感器搜索前后的目标位置不确定性减少量的反映，常作为传感器搜索调度的准则.定义t时刻选择的搜索区域为k（t），则信息增益函数EI可表示为

EI（t，k（t））=∑1j=0D·（P（Hk=1|zk（t）=j，k（t）），pki（t-1））·P（zk（t）=j|k（t）），  （6）

式中D·表示式（1）～（3）的3种常用信息测度;P（zk（t）=j|k（t））表示t时刻所选搜索区域k（t）的观测结果，可由下式预测

P（zk（t）|k（t））=∑1j=0P（zk（t）|Hk（t）=j，k（t））·P（Hk（t）=j）.         （7）

文献[2]经分析还提出一种全局信息增益EG，反映了目标检测结果对所有搜索区域信息增益的影响，定义为

EG（t，k（t））=∑nk=1∑1j=0D·（P（Hk=1|zk（t）=j，k（t）），pki（t-1））·P（zk（t）=j|k（t））. （8）

相应地，本文称式（6）的信息增益为局部信息增益.

在信息增益准则下，通过信息增益最大化选择区域进行搜索.引入传感器观测能力约束和捕获时效性约束，可建立如下搜索调度模型

max{E·（t，k（t）），k（t）∈{1，2，…，n}}

s.t.Tj∈S，

1fk<tk，k=1，2，…，n，（9）

式中E·表示式（6）或式（8）的信息增益函数，Tj∈S表示目标Tj在传感器S的观测范围内，1fk<tk表示传感器完成一次探测的时间（等于探测数据率的倒数）小于在该搜索区域的驻留时间.

分别采用式（1）～（3）的3种信息测度与式（6）和式（8）两种信息增益函数，可以得到6种典型的基于信息增益的传感器搜索调度模型：基于全局Shannon熵增益的搜索调度（SSGShannon）;基于全局KullbackLeibler熵增益的搜索调度（SSGKL）;基于全局Rényi熵增益的搜索调度（SSGRényi）;基于局部Shannon熵增益的搜索调度（SSLShannon）;基于局部KullbackLeibler熵增益的搜索调度（SSLKL）和基于局部Rényi熵增益的搜索调度（SSLRényi）.

2搜索性能仿真对比分析

为确定传感器搜索调度方法对目标捕获性能提高的程度，需要比较搜索调度方法和无调度方法的性能.在现有研究中，主要有两种无调度方法，即顺序搜索（SQS， Sequential Search）和随意搜索（RDS， Random Search）[10，11].对于SQS方法，传感器按照各搜索区域的编号依次搜索，搜索完最后一个区域时，重新从第一个区域开始顺次搜索;对于RDS方法，传感器每次观测都随意选择一个区域进行搜索，且以同等概率选择任一区域.

本文仿真对比分析了6种基于信息增益的搜索调度方法和两种无调度方法，并采用目标累积捕获概率评价搜索调度方法性能.多帧累积捕获概率pcc定义为：n帧捕获中有不小于m帧成功捕获目标的概率，即

pcc（l≥m）=∑ni=mpcc（i）=∑ni=m（n

i）·pic·（1-pc）n-i，（10）

式中l表示n帧捕获中成功捕获到目标的帧数，pcc（i）为n帧捕获中有i帧成功捕获到目标的累积捕获概率.本文仿真试验中取m=1，则有

pcc（l≥1）=∑ni=1（n

i）·pic·（1-pc）n-i=1-（1-pd·pi）n.（11）

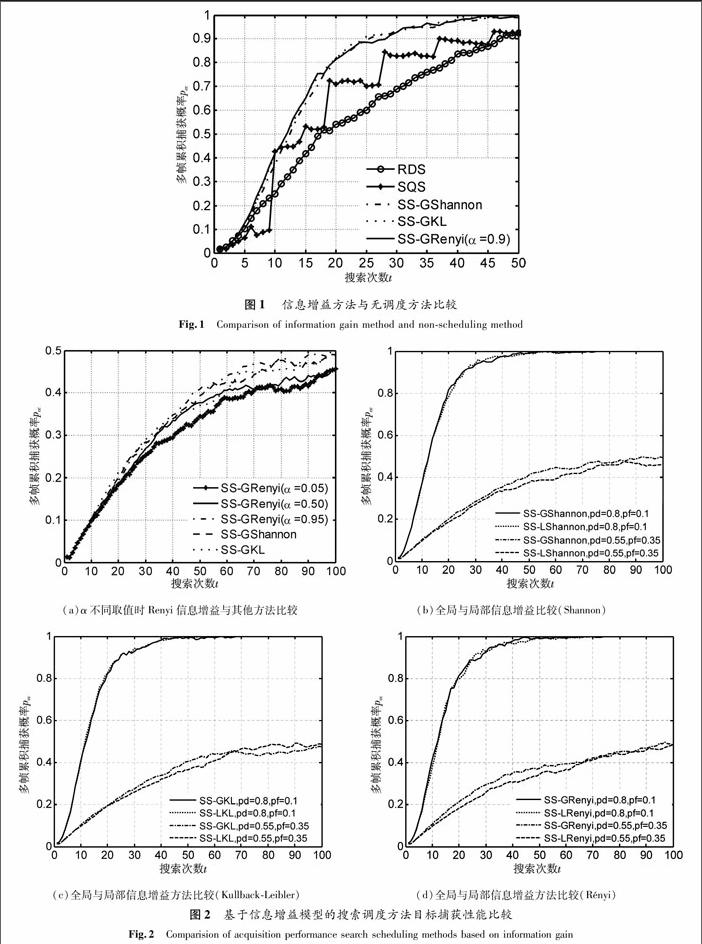
各种方法调度传感器观测目标的累积捕获概率结果（200次MonteCarlo实验平均值）如图1所示.仿真场景设置为：传感器执行3×3=9的搜索，各搜索区域的初始截获概率为pi（0）=[0.021 7，0.103 9，0.021 7，0.103 8，0.498 0，0.103 9，0.021 6，0.103 8，0.021 7].

图1信息增益方法与无调度方法比较

Fig.1Comparison of information gain method and nonscheduling method6种信息增益模型调度传感器观测目标的累积捕获概率结果（200次MonteCarlo实验平均值）如图2所示，其仿真场景设置同图1，且图2（a）取pd=0.55，pf=0.35，图2 （d）的Rényi熵α参数取α=0.9.

（a）α不同取值时Renyi信息增益与其他方法比较  （b）全局与局部信息增益比较（Shannon） （c）全局与局部信息增益方法比较（KullbackLeibler） （d）全局与局部信息增益方法比较（Rényi）

图2基于信息增益模型的搜索调度方法目标捕获性能比较

Fig.2Comparision of acquisition performance search scheduling methods based on information gain由图1和图2可得如下结论：

（1） 各种基于信息增益的搜索调度方法对目标的捕获性能明显优于无调度的SQS方法和RDS方法.

（2） 基于Shannon和KullbackLeibler信息增益的搜索调度方法对目标的捕获性能差别很小;而基于Rényi信息增益的搜索调度方法对目标的捕获性能随参数α取值的增大而提高，α→1时性能最优，且与基于Shannon和KullbackLeibler信息增益的方法性能相当.

（3） 对于Shannon，KullbackLeibler，Rényi这3种信息测度来说，随着检测概率减小（或虚警概率增大），全局信息增益方法在捕获性能上逐渐表现出优势，这是由于全局信息增益充分考虑了所有搜索区域信息量变化的缘故.

3结论

本文针对目标搜索传感器调度问题展开研究，首先介绍了Shannon熵、KullbackLeibler熵和Rényi熵3种信息测度以及全局信息增益和局部信息增益的数学定义;然后基于这3种信息测度和两种信息增益，建立了6种基于信息增益的目标搜索传感器调度模型;最后，通过数值仿真计算，对比分析了6种基于信息增益的搜索调度方法与两种无调度方法调度传感器对目标的捕获性能.仿真结果表明，基于信息增益模型的搜索调度方法的目标捕获性能明显优于无调度方法，且基于全局信息增益模型的搜索调度方法性能更优.仿真结果可作为实际工程实践中优选搜索调度方法的参考.进一步的研究工作可从以下两方面展开：（1）基于信息增益模型的搜索调度方法在不同应用领域、不同先验条件下对目标的搜索捕获性能研究;（2）不同体制传感器对同一目标联合探测条件下，多种传感器的联合搜索调度问题.

参考文献：

[1]MATTHIESEN D J. Optimal search[C]∥Proceedings of the IEEE international symposium on phased array systems and technology. Boston， 2003：259264.

[2]卢建斌. 相控阵雷达资源优化管理的理论与方法[D]. 长沙： 国防科技大学， 2007.

[3]DONALD R D， HEMSTETER K P. GRASP multisensor search tactics against evading targets[C]∥Proceedings of MTS/IEEE oceans 02 conference. Biloxi， 2002：5459.

[4]CHRISTOPHER G. Active target search from UAVs in urban environments[C]∥Proceedings of the IEEE international conference on robotics and automation. Pasadena， 2008：23662371.

[5]占红来. 红外弱小目标搜索跟踪算法研究[D]. 北京： 中国工程物理研究院， 2013.

[6]JAMES N E， JAMES R Y. An approximate solution technique for the constrained search path moving target search problem[R]. California， USA： Naval Postgraduate School， 1985.

[7]STONE L D. Theory of optimal search[M]. New York： Academic Press， 1975.

[8]徐斌，杨晨阳，李少洪，等. 相控阵雷达的最优分区搜索算法[J]. 电子学报， 2000，28（12）：6973.

[9]MARK P K， LESLIE M C. Informationbased sensor management in the presence of uncertainty[J]. IEEE TSP，  2007，55（6）：27312735.

[10]MARK P K， LESLIE M C. Analysis of an informationbased sensor manager applicable to landmine detection[C]∥Proceedings of the IEEE international geosicience and remote sensing symposium. Boston， 2008：521524.

[11]WANG B， LI J， AN W， et al. Information gain based sensor search scheduling for the lowearth orbit constellation[J]. J Syst Eng Electr， 2011，22（6）：926932.

[12]KREUCHER C M， KASTELLA K D， HERO A O. Information based sensor management for multitarget tracking[C]∥Proceedings of the SPIE signal and data processing of small targets. San Diego， 2003：480489.

[13]厉亚，王博，吴洪. 基于高斯误差椭球的截获概率仿真[J]. 湖南大学学报：自然科学版， 2013，40（11）：108113.

[14]沈东，魏瑞轩，祁晓明，等. 基于MTPM和DPM的多无人机协同广域目标搜索滚动时域决策[J]. 自动化学报， 2014，40（7）：13911403.

[15]毛弋，蒋盈，李宝玉，等.多种通信方式并存的配网自动化通信系统的研究[J].湖南师范大学自然科学学报， 2013，36（4）：3136.