关于钢筋混凝土叠合梁叠合面抗剪设计的讨论
2015-12-11任彧
任 彧
(福建省建筑设计研究院 福建福州 350001)
问题的提出
随着我国新型建筑工业化工作的推进和展开,装配整体式结构的设计方法成为当前结构设计工作的热点问题。许多省份先后颁布了装配整体式混凝土结构的地方规程。
叠合楼盖是装配整体式结构的重要组成部分,叠合面的存在是装配整体式结构与现浇结构的本质差别。已颁布的各地方规程的条文,对于叠合面抗剪问题却给出了不同的解决方式。其中:深圳规程、辽宁规程给出了基于剪应力的计算公式;湖南规程、安徽规程、上海规程则直接引用了《混凝土结构设计规范》GB50010-2010附录H的规定。如何正确地计算叠合面的抗剪承载力就成了结构设计中急需明确的问题。
1 叠合面剪应力的计算
深圳规程SJG18-2009[1]第6.3.4条指出:水平叠合面剪应力按τ=计算。这是一个经典的材料力学公式,粗看之下并无问题;但是,这个经典公式是基于变形符合平截面假定和材料线弹性假定得出的,截面应力分布如(图1)所示。
可是即使在正常使用极限状态下,普通钢筋混凝土抗弯构件也是带裂缝工作的,横截面上的正应力并非线性分布。通常假定受压区混凝土均匀受压,受拉区仅钢筋承受拉力;根据剪应力是计算截面以上正应力的积分这个原则,可绘出钢筋混凝土受弯构件的截面应力分布,如(图2)所示。利用截面剪力的大小等于剪应力图形面积的原则,通过简单的几何计算可知:
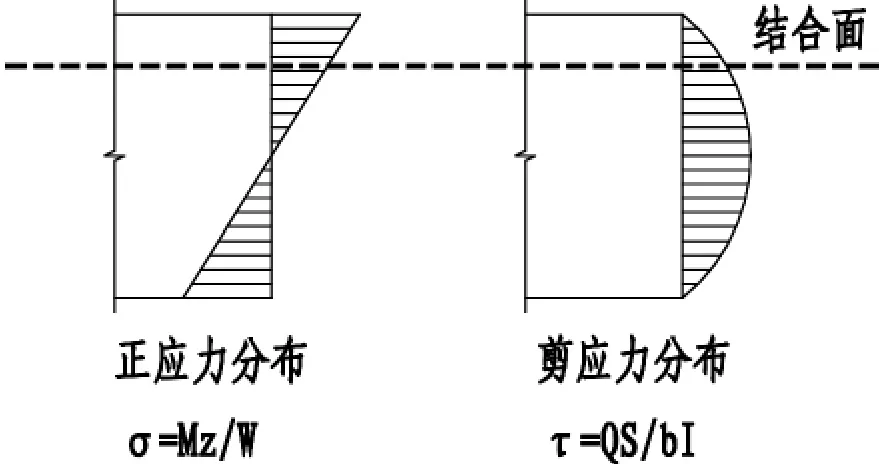
图1 线弹性弯曲构件的截面应力分布
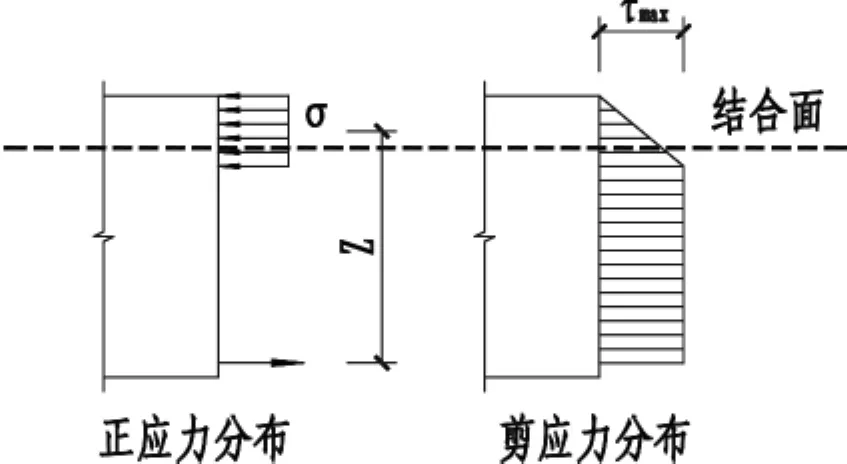
图2 钢筋混凝土受弯构件的截面应力分布

式中:z为受拉钢筋作用点至混凝土受压区合力中心的距离,即受弯截面的力臂;b为受弯构件的宽度。由于混凝土受压区范围内剪应力分布为线性,利用几何相似性可知,叠合面处的剪应力可按下式计算:

式中:β为叠合面至受压边缘的混凝土受压面积与混凝土总受压面积的比值。其余符号说明同(1)式。
因此,深圳规程的水平叠合面剪应力公式不适用于普通混凝土构件,可用于未开裂的预应力混凝土受弯构件。
2 计算对象的选定
叠合受弯构件叠合面抗剪失效的后果必然是新旧混凝土间发生了相对水平错动。因此,取叠合面以上的现浇区域作为计算隔离体显然是合适的。问题在于该隔离体在纵向上的长度应如何取值。
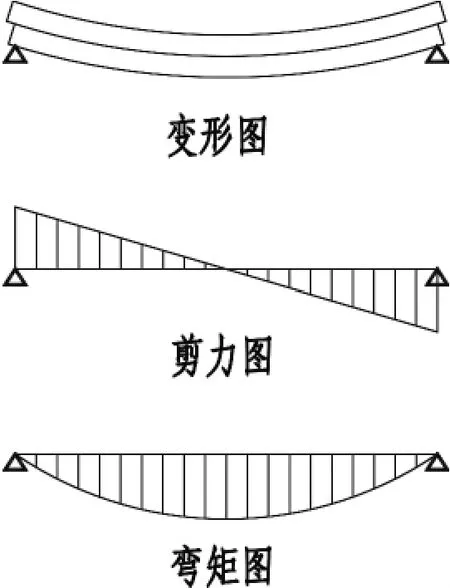
图3 单跨简支梁内力变形图
以承受均布荷载的单跨简支梁为例,(图3)给出了叠合面失效时叠合梁的变形以及相应的内力图。我们不难发现在弯矩极值点两侧的剪力反号,说明弯矩极值点两侧的错动变形趋势的方向相反,两侧结合面的抗剪验算并无关联。因此,对于简支梁应该以弯矩极值点为界,对两侧分别进行叠合面抗剪验算。
对于多跨连续叠合梁,水平叠合面的抗剪承载力验算应以支座点、弯矩绝对值最大点和零弯矩点为界限,划分为若干剪跨区段分别进行验算。各剪跨区段内,叠合面上剪应力均同向。

图4 叠合梁剪跨区段的划分
弯矩为零的截面处,混凝土受压区压应力为零。如果隔离体在长度方向上取|Mmax|点至弯矩零点(图5),可以利用水平方向力的平衡条件建立如下公式

式中:τ为水平叠合面剪应力;Ac为叠合面以上混凝土等效截面的受压区面积;Ach为叠合面面积;σ为混凝土压应力。公式(3)等号左侧即为剪跨内水平叠合面处的总剪力V。
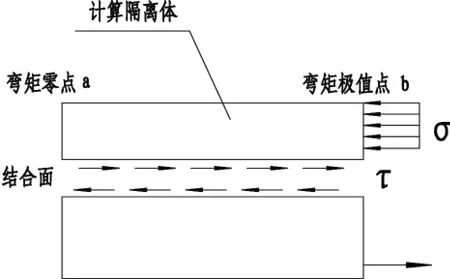
图5 计算隔离体
因此,可以通过剪跨区内|Mmax|处,叠合面以上的混凝土受压区总轴力来求得水平叠合面的总剪力。叠合面抗剪承载力的设计目标应该是:该破坏模式不应先于其他破坏模式出现。所以,(3)式等号右侧的σ可用混凝土抗压强度设计值fc替代。水平叠合面抗剪验算中,剪跨单元的水平总剪力可按下式计算:

利用(4)式可以避免对剪应力进行复杂的积分运算。现行《钢结构设计规范》GB50017-2003[2]第11.3.4条的正文及条文解释中指出:“栓钉等柔性抗剪连接件具有很好的剪力重分布能力,可按剪跨区段均匀布置连接件”。叠合梁中的箍筋显然属于柔性抗剪连接件,因此以剪跨划分计算隔离体,对各隔离体分别进行叠合面抗剪验算是可行的。
3 混凝土规范公式H.0.4-1存在的问题
现行《混凝土结构设计规范》GB50010 -2010[3]的第H.0.4条指出:叠合面受剪承载力应符合以下要求:

公式(3)系沿用GBJ10-89第7.5.5条的规定。该条文是基于周旺华教授担任课题组组长的《叠合结构应用课题组》的研究成果。为便于大家理解公式的来龙去脉,现将周旺华教授的专著《现代混凝土叠合结构》[4]中第五章第2节的相关内容原文引述如下:
规范编制组根据49个剪切试件试验结果得到线性回归公式:
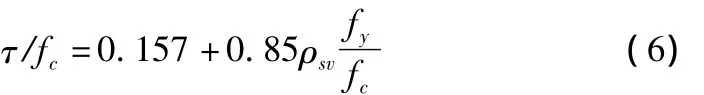

图6 叠合梁叠合面计算模型
利用(图6)所示的脱离体作为计算模型,在不考虑箍筋作用的假设条件下建立剪切试验结果与叠合面抗剪强度之间的关系。由力矩平衡条件可得V·a=D·z

考虑到叠合梁抗剪试验中较少出现斜裂缝沿水平叠合面发展的情况,建议设计计算公式适当偏高取用,即取
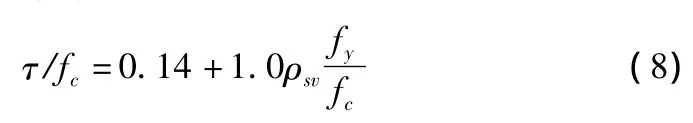
再利用公式(7),并按通常做法,近似取z=0.85h0,则可得叠合面抗剪计算公式如下:

对上述公式的推导过程,我们存在如下疑问:
(1)图6的隔离体明显属于斜截面破坏模式,是否适于推导叠合面剪切破坏公式?
(2)因为试验结果与ρsv相关的,所以试件显然是配置箍筋的。穿越隔离体的箍筋拉力对于弯矩平衡必然是有影响的,公式(5)推导过程中不考虑箍筋的假设能否成立?
(3)公式(5)与本文推导的公式(2)相差β,显然公式(5)未考虑叠合面位置的影响,是否合理?
(4)“考虑到叠合梁抗剪试验中较少出现斜裂缝沿水平叠合面发展的情况”[4]的提法是否混淆了叠合面抗剪与斜截面抗剪两种不同的破坏模式?
(5)由推导过程可知,公式左侧的V是试件的端剪力,与叠合面抗剪破坏模式的验算隔离体并不直接相关。
综上所述:规范公式H.0.4-1在正文和条文解释中均没有明确计算对象,对于公式左侧的V的计算方法未作说明;且公式的形式与斜截面受剪承载力公式相似,容易误导设计人员按照斜截面验算的习惯,对梁端部截面的剪力进行验算。事实上,叠合面抗剪与斜截面抗剪是完全不同的2种破坏模式,计算剪力的取用也完全不同。
4 叠合面抗剪的摩擦剪切模型
对于叠合面抗剪承载力的计算,Birkeland[5]最早提出的摩擦抗剪模型。该模型认为:沿着剪切平面的裂缝先于剪力作用形成;当剪力作用时,由于裂缝处凹凸不平,裂缝两侧在发生滑移的同时也产生分离,使得穿过剪切平面的钢筋产生拉力,从而在钢筋附近的混凝土中产生压力,沿着剪切平面就产生了摩擦抗剪强度。在抗剪钢筋适当锚固且配筋率适当的条件下,当钢筋中的拉应力达到屈服强度时,认为抗剪承载力失效。
部分学者[6,7]对摩擦抗剪模型提出了修正:穿过剪切平面的钢筋中产生的拉力的水平分量即为钢筋的销栓作用,可直接抵抗剪力;拉力的垂直分量在钢筋附近的混凝土中产生压力,通过摩擦作用抗剪;裂缝处突出物咬合点的直接承压也是剪力传递的重要途径(图7)。当以上三者的抗剪能力之和小于作用剪力时,即认为抗剪承载力失效。
5 各国叠合面抗剪承载力计算方法的比较
美国规范关于叠合面抗剪的剪切摩擦方法最早出现在ACI318-71规范中。最新版本的ACI318-2011[8]规范给出的叠合面抗剪承载力公式为

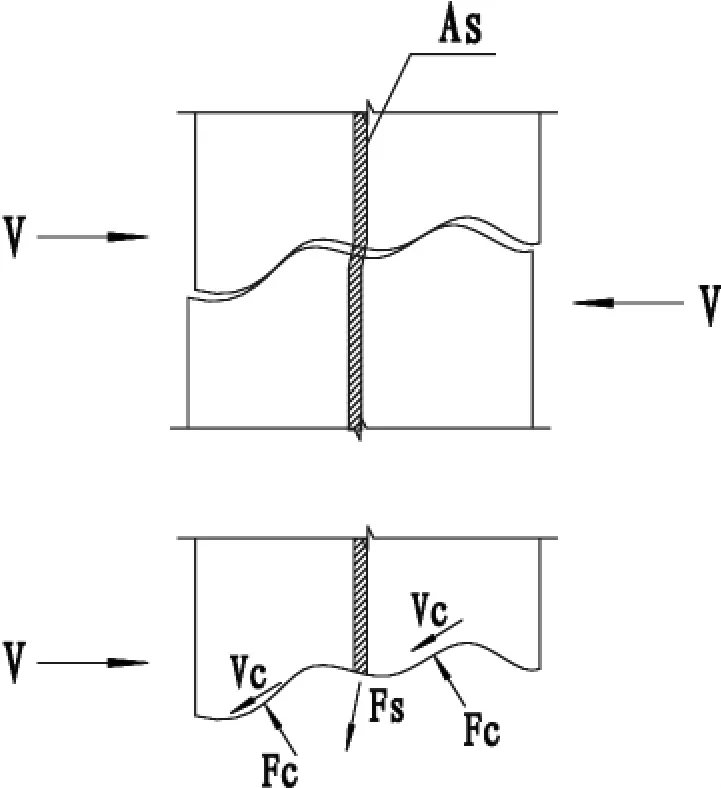
图7 修正的摩擦剪切模型
式中:Vn为剪切面的名义抗剪能力;Ac为混凝土叠合面面积;Avf为剪切摩擦钢筋面积;fy为剪切摩擦钢筋强度设计值;μ为摩擦系数:对于整体浇筑的混凝土为1.4λ,对于粗糙化处理的叠合面为1.0λ,对于未经粗糙化处理的叠合面为0.7λ,对于普通混凝土λ=1;α为剪切摩擦钢筋与叠合面的夹角。该公式以结构受荷前已有裂缝为前提,比较保守。为此,ACI318-2011的条文说明中还给出了下面的计算公式:
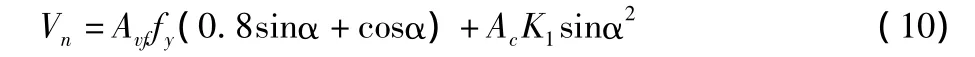
式中:K1为与混凝土品种有关的量。对于普通混凝土,K1=400psi(2.758MPa),其余符号同公式(9)。
欧洲规范 EN1992-1-1:2004[9]规定,叠合面抗剪强度设计值vRdi按下式计算:

式中:fctd为混凝土抗拉强度设计值;σn为叠合面上法向外力产生的应力;ρ为摩擦抗剪钢筋面积与叠合面面积的比值;α为剪切摩擦钢筋与叠合面的夹角;c、μ为与叠合面粗糙度相关的系数,对于未经粗糙化处理的叠合面:c=0.35,μ=0.6,对于粗糙化处理的叠合面 c=0.45,μ =0.7;v为有效系数,v=0.6(1-fck/250)。
将公式(11)等号两侧均乘以叠合面面积Ach;对于叠合受弯构件可忽略法向应力的影响,可得:

显然公式(9)是基于剪切摩擦模型,公式(10)、(12)则是基于修正剪切摩擦模型。
注意到在ACI规范及欧洲规范的相应公式中均未出现梁高h0。相同界面的不同梁高的叠合梁在叠合面处具有同样的界面结合强度,这个结论显然是符合工程逻辑的。因此,中国规范公式H.0.4-1中在承载能力一侧出现梁高h0是不合适的,有概念不清的嫌疑。
6 叠合面粗糙度相关的系数的讨论
根据前面的讨论可知,公式(12)可以体现修正剪切摩擦模型的主要结论,是叠合面抗剪承载力计算的通式。根据规范编制组给出的公式(6)比照公式(12)的形式进行整理,可得τ=0.157fc+0.85ρfyd,在等号两侧乘以叠合面面积 Ach,并对符号下标进行统一,可得:

为确认c、μ取值的影响,在相同条件下,对各国规范公式计算结果进行了试算对比。相关参数设定以实际工程为背景:叠合楼盖的混凝土强度等级为C25~C35;箍筋的直径为Φ8~12、3级钢、箍筋间距为100mm~200mm,箍筋垂直于叠合面;假定叠合面进行了粗糙化处理;叠合面宽度250、长度1000。计算时考虑了各国规范对于混凝土强度取值的差异。


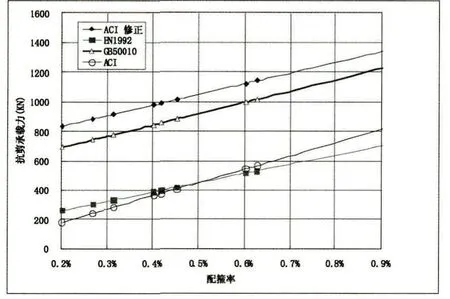
图10 各国规范计算抗剪承载力对比(C35)
由(图8~图10)可知,在同等条件下,按照公式(13)计算的叠合面抗剪承载力略低于ACI修正公式(11)的计算值,但高于欧洲规范公式(12)和ACI正文公式(9)的计算值。需要指出,ACI公式在进行强度验算时,需对计算出的抗剪承载力乘以0.75的强度折减系数。因此,中国规范公式给出的水平叠合面抗剪承载力是相对偏高的。
考虑到公式(13)未考虑抗剪钢筋与叠合面斜交的情况,参考ACI公式,将公式(13)式修正如下:

图11 考虑强度折减后各国规范计算抗剪承载力对比(C30)
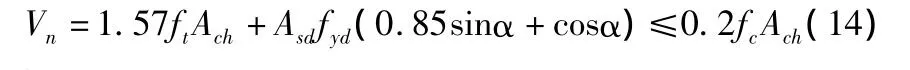
式中:Vn为剪切面的名义抗剪能力;ft为混凝土抗拉强度设计值;fc为混凝土抗压强度设计值;Ach为混凝土叠合面面积;Asd为抗剪钢筋面积;fy为抗剪钢筋强度设计值;α为抗剪钢筋与叠合面的夹角。
注意到ACI规范条文说明中指出,使用修正剪切摩擦计算方法时,为保证设计公式有效,要求 Avffy/Ac>200 Psi(1.38Mpa)。ACI规范对于最小配筋的限值规定是较为严格的,如箍筋为3级钢,换算为中国工程师习惯的配箍率为0.38%。
7 结论与建议
(1)叠合受弯构件的剪应力计算可按照本文公式(2)进行。
(2)现行《混凝土设计规范》GB50010公式H.0.4-1在形式上欠妥。
(3)水平叠合面的抗剪承载力验算应以支座点、弯矩绝对值最大点和零弯矩点为界限,划分为若干剪跨区分别进行验算。
(4)依据现行规范的编制条件,可按照Vn=1.57ftAch+Asdfyd(0.85sinα+cosα)计算叠合面抗剪承载力;抗剪钢筋最小配箍率建议较现行规范限值适度提高。
[1]SJG18-2009,预制装配整体式钢筋混凝土结构技术规范[S].
[2]GB50017-2003,钢结构设计规范[S].
[3]GB50010-2010,混凝土结构设计规范[S].
[4]周旺华现代混凝土叠合结构[M].北京:中国建筑工业出版社,1998.
[5]Birkeland P W,Birkeland H W.Connections in precast concrete construction[J].Journal of American Concrete Institute,1966,63(3):345.368.
[6]Mattock A H.Cyclic sheat transfer and type of interface[J].Journal of the Structural Division,ASCE,1981,107(STIO):1945 -1963.
[7]Hofbeck J A,Ibrahim I O,Mattock A H.Shear transfer in reinforced concrete[J].ACI Journal,Proceedings,1969,66(2):119 -128.
[8]ACI Committee 318.ACl318 -2011 Building Code Requirements for Reinforced Concrete[S].Farmington Hills:American Concrete Institute,2011.
[9]EN1992-1-1:2004.Eurocode 2:Design of concrete structures Part 1- 1:General rules and rules for buildings[S].European Committee for Standardization,2004.
