Development and Optimization of an Unstructured Kinetic Model for Sodium Gluconate Fermentation Process

Yaming Dong,Xuefeng Yan,2,Fei Lu,Meijin Guo,Yingping Zhuang

Development and Optimization of an Unstructured Kinetic Model for Sodium Gluconate Fermentation Process

Yaming Dong1,Xuefeng Yan1,2,Fei Lu3,Meijin Guo3,Yingping Zhuang3

This study proposed a modified unstructured kinetic model for sodium gluconate fermentation byAspergillus niger.Four specific growth rate equations(Monod,Tessier,Contois,and logistic)were considered in the biomass growth equation.The growth,instantaneous biomass concentration,instantaneous product,and substrate concentration were considered in the equations of product formation and substrate consumption.Option parameters were introduced to determine the form of the unstructured model.A double-nested optimization strategy was proposed to optimize the option and kinetic parameters.The proposed unstructured kinetic model based on the estimated optimal parameters efficiently simulated sodium gluconate fermentation.The obtained option parameters of the kinetic model indicated that the Monod equation-based unstructured model displayed better performance than the three other specific growth rate equation-based kinetic models.

Fermentation;Growth kinetics;Kinetic parameters;Optimization;Sodium gluconate;Unstructured kinetic model.

1 Introduction

Gluconic acid and its salt sodium gluconate are bulk chemicals with many uses in the food,pharmaceutical,detergent,leather,and beverage industries[Das and Kundu(1987);Milsom and Merers(1985);Sawyer(1964)].The future of these applications principally depends on the commercial availability of gluconates.Gluconic acid is produced via submerged fermentation using strains ofAspergillus nigerand glucose as the carbon source[Singh and Kumar(2007)].Gluconic acid production byA.nigeris an aerobic fermentation with a high oxygen demand, and the biotrans-formation of glucose to gluconic acid represents a simple dehydrogenation reaction without the involvement of complex metabolic cell pathways[Znad,Markoš,and Baleš(2004)].

Kinetic models are useful because they enable engineers to design and control industrial processes[Gianoli,Fisher,Maeder,and Hungerbühler(2007);Salmi,Murzin,Mäki-Arvela,Kusema,Holmbom,Willför,and Wämå(2014);Zhang,Yang,Zhu,Li,and Gui(2013)].The behavior of these processes can be evaluated more rapidly and accurately with kinetic models than laboratory analytical methods only.Two types of kinetic models are available for the microbial process:structured[Mustafa,Elkamel,Lohi,Ibrahim,and Elnashaie(2014)]and unstructured[Schill,Van Gulik,Voisard,and Von Stockar(1996)].Structured models consider certain basic principles of cell structure,function,and composition,whereas unstructured models describe the biological system only by cell mass[Znad,Blazej,Bales,and Markos(2004)].

Many scholars have investigated the kinetic modeling of gluconic acid byA.niger.Takamatsu et al.developed a structured model to describe gluconic acid fermentation byA.niger[Takamatsu,Shioya,and Furuya(1981)].Liu et al.proposed a simple unstructured model in which the logistic equation was used for cell growth,the Luedeking-Piret equation for gluconic acid production,and the Luedeking-Piretlike equation for glucose consumption[Liu,Weng,Zhang,Xu,and Ji(2003)].Znad et al.proposed an unstructured model for gluconic acid fermentation byA.niger[Znad,Blazej,Bales,and Markos(2004)].The Contois-type model was used to simulate growth.The obtained results show that gluconic acid production is mostly associated with growth.

Although structured models can describe cell activities,they are complicated for normal use because they require more equations to solve as compared with unstructured models.Several equations are required to describe cell growth,substrate consumption,and product formation for unstructured models;thus,these models are much easier and faster to develop than structured models and can accurately predict the behavior of fermentation processes[Feng,Zhang,Jia,Yang,Liu,and Lin(2014);Jang and Barford(2000)].

The most difficult and important step in modeling fermentation is to determine the form of the specific growth rate expression µ,which can describe the cell growth accurately.The Monod equation is one of the earliest and most widely used unstructured models to describe cell growth[Monod(1949)].Much more sophisticated models such as the Tessier,Contois,and logistic equations have been proposed to describe cell growth.In our previous work[Dong,Fan,Yan,Guo,and Lu(2014)],a back propagation neural network(BPNN)was used to model the mycelium growth rate of sodium gluconate fermentation without considering the mechanism of the process.

However,how to determine the appropriate form of an unstructured model for a given fermentation process remains an open issue.Therefore,the present research aims to develop a modified unstructured kinetic model for gluconic acid production byA.niger.Four specific growth rate equations(Monod,Tessier,Contois,and logistic)were considered in the biomass growth equation.The growth,instantaneous biomass concentration,instantaneous product,and substrate concentration were considered in the equations of product formation and substrate consumption.Option parameters were introduced to determine the appropriate form of kinetic model.A double-nested optimization strategy was proposed to search the optimal option and kinetic parameters for the unstructured model.The experimental fermentation data obtained from a 50 L batch fermenter of sodium gluconate byA.nigerwere used to develop and evaluate the performance of the unstructured kinetic model.

The remainder of the paper is organized as follows.Section 2 describes the experimental setup and procedure.Section 3 introduces the unstructured kinetic model of sodium gluconate fermentation.In Section 4,a modified unstructured kinetic model is proposed and optimized using a double-nested optimization strategy.Section 5 contains the results and discussion.Section 6 concludes the paper.

2 Experimental setup and procedure

The experimental setup and procedure are described in detail by our previous work[Dong,Fan,Yan,Guo,and Lu(2014)].In brief,they were described in the following.

2.1 Culture conditions

A.niger(AN14)with high activities of glucose oxidase and catalase was obtained from the National Engineering Research Center of Biotechnology,Shanghai,China.

The fungus was grown in a 15 L tank with a working volume of 9 L and stirred with a rotary shaker at 300 rpm and 38°C for 20 h.The air f l ow and pressure were 600 L/h and 0.1 MPa,respectively.The inoculum medium contained 6.0%glucose,2.0%agar,0.3%corn steep liquor,0.05%CON2H4,0.03%KH2PO4,and 0.005%MgSO4·7H2O.Mycelium was transferred to the fermentation reactor after its formation(15%inoculation ratio).

Sodium gluconate fermentation was carried out in a 50 L stirred tank bioreactor with a working volume of 33 L.The fermentation medium contained 6.0%glucose,2.0%agar,0.1%corn steep liquor,0.02%CON2H4,0.013%KH2PO4,and 0.002%MgSO4·7H2O.A defoamer was used to reduce foaming.The fermentation conditions were as follows:air f l ow,1200 L/h;agitation rate,500 rpm;pressure,0.1 MPa;and temperature,38°C.The pH was controlled at 5.8 using 20%(v/v)NaOH.

2.2 Analytical methods

During fermentation,the following parameters were measured and recorded online:dissolved oxygen concentration,pH,temperature,agitation rate,air f l ow,pressure of inlet and outlet gas streams,and volume.

The biomass concentration was calculated by mycelial dry weight,which was determined through a gravimetric method.The mycelial suspension was filtered,washed several times with distilled water,and then dried to a constant weight at 80°C.The filtrate was subjected to high-performance liquid chromatography(HPLC).The gluconic acid concentration was determined by HPLC analysis with a UV detector.Fehling’s test was performed to determine glucose concentration.The experimental errors of the measurements are approximately 3%to 5%.

3 Unstructured kinetic model

The rate equations of biomass(X),sodium gluconate(P),and glucose(S)were used for the model to describe the fermentation process.The material balances of the biomass,sodium gluconate,and glucose can be written as

with the initial conditions att=0,

where the formation ratesrX,rP,andrSshould be described by the appropriate unstructured kinetic models.

3.1 Biomass growth

The Monod equation is one of the most widely used models to describe cell growth[Monod(1949)].This model is deterministic,distributed,and unstructured.The biomass growth can be defined as

where µ is the specific growth rate and can be given by the Monod equation as

where µmaxis the maximum specific growth rate,andKSis the substrate saturation constant.

Sophisticated models such as the Tessier,Contois,and logistic equations were also proposed to describe the specific growth rate.The expressions of these equations are listed in Table 1.

Table 1:Expressions of specific growth rate equations.

3.2 Product formation

The kinetics of gluconic acid formation was based on the Luedeking-Piret equation[Luedeking and Piret(1959)].This model was first developed for lactic acid formation.This unstructured model shows that product formation is associated with growth and non-growth contributions.The product formation can be described as

where α and β are the kinetic parameters for growth-and non-growth-associated product formation,respectively.

3.3 Substrate consumption

Glucose is used in the formation of cell materials and metabolic products,as well as in the maintenance of cells.The kinetics of glucose consumption was based on a Luedeking-Piret-like equation.The substrate consumption can be described as

whereYX/Sis the yield coefficient,andmSis the maintenance coefficient.

4 Kinetic model optimization

4.1 modified unstructured kinetic model

On the basis of the unstructured model of sodium gluconate fermentation provided in Section 3,a modified unstructured kinetic model was proposed and described as

wherek1,k2,k3,k4are the introduced option parameters to determine the form of the biomass growth;m1,m2,···,m8are the introduced option parameters to determine the form of product formation and substrate consumption;anda1,a2,···,a8are the kinetic parameters of the unstructured model.

Four specific growth rate equations(Monod,Tessier,Contois,and logistic)were considered in the biomass growth equation for the proposed modified unstructured model.The option parameters ofk1,k2,k3,k4were used to select one that can describe the biomass growth.The values ofk1,k2,k3,k4are 0 or 1,andThe growth,instantaneous biomass concentrationX,instantaneous productP,and substrate concentrationSwere considered in the equations of product formation and substrate consumption.The option parametersm1,m2,···,m8were used to determine the appropriate form that can accurately describe the product formation and substrate consumption.The values ofm1,m2,···,m8are random 0 or 1.

4.2 Model parameter optimization

For the unstructured model proposed in Section 4.1,two types of parameters(i.e.,option and kinetic)need to be determined before the kinetic model can be used to describe fermentation.The option parameters were used to determine the form of the unstructured model,and their values should be the integer 0 or 1.If the value of the option parameter is 1,then the influence of this part multiplied by it is considered in the kinetic model equation.If the value of the option parameter is 0,then its influence is ignored.To obtain a relevant kinetic model,the kinetic parameters should be estimated by comparing the assumed kinetic model with the experimental data after the option parameters are determined.

Figure 1:Flowchart of the double-nested optimization strategy.

In the present study,a double-nested optimization strategy was proposed to optimize the unstructured kinetic model.In the fi rst step,the option parameters were determined with the 0-1 programming method.In the second step,the kinetic parameters were estimated by minimizing the difference between the model simulation results and the experimental data.The second process is similar to the estimation process in the reference[Praveen and Sinha(2009)].Iterations were performed between two steps until the convergence.The simplex method was employed as an optimizer to estimate the kinetic parameters.The optimization objective was defined as follows:

After the optimal option and kinetic parameters were determined by the double-nested optimization strategy,the optimal form of the proposed unstructured kinetic model was developed,and the obtained kinetic model was used to simulate the fermentation process.

5 Results and discussion

5.1 Model performance evaluation indices

Two model evaluation indices were used to analyze the obtained unstructured model statistically.These indices were described as

Root mean squared error:

Table 2:Optimal values of the option and kinetic parameters of the four unstructured kinetic models.

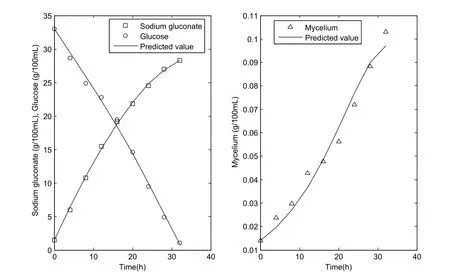
Figure 2:Simulation results of the obtained optimal unstructured kinetic model based on the Monod equation.

5.2 Kinetic model performance

In accordance with the 0-1 programming method,four biomass growth models were obtained when one ofki(i=1,2,3,4)is equal to 1.The four biomass growth models were based on the Monod,Tessier,Contois,and logistic equations.With the double-nested optimization strategy,the optimal values of the option and kinetic parameters of these four unstructured kinetic models were obtained and are listed in Table 2.The simulation results of the four unstructured kinetic models with the obtained optimal parameters are shown in Figures 2 to 5.The figures show that the obtained unstructured kinetic models displayed satisfactory performances.The evaluation indices RMSE and RE were calculated to evaluate further the performances of the four unstructured kinetic models.The results are listed in Table 3,and the best results are shown in bold.Table 3 shows that the Monod-based unstructured kinetic model with the obtained optimal option and kinetic parameters had the least RMSE and RE values.These results show that the optimal option and kinetic parameters can be determined using the proposed double-nested optimization strategy and that the developed unstructured kinetic model based on the Monod equation demonstrated a good performance in simulating gluconate acid fermentation.

Figure 3:Simulation results of the obtained optimal unstructured kinetic model based on the Tessier equation.

Figure 4:Simulation results of the obtained optimal unstructured kinetic model based on the Contois equation.

Figure 5:Simulation results of the obtained optimal unstructured kinetic model based on the logistic equation.

Table 3:RMSE and RE of the four unstructured kinetic models.

6 Conclusions

This study proposed a modified unstructured kinetic model for sodium gluconate fermentation byA.niger.Four specific growth rate equations were considered in the biomass growth equation.The growththe instantaneous biomass concentrationX,the instantaneous productP,and the substrate concentrationSwere considered in the equations of product formation and substrate consumption.A double-nested optimization strategy was proposed to optimize the unstructured kinetic model option and kinetic parameters.Results showed that the optimal parameters can be determined by the proposed optimization strategy.The modified unstructured kinetic model with the obtained optimal parameters efficiently simulated sodium gluconate fermentation.The Monod equation-based unstructured kinetic model demonstrated better performance than the three other biomass growth equation-based models.

Acknowledgement:The authors gratefully acknowledge the support from the following foundations:973 project of China(2013CB733600),National Natural Science Foundation of China(21176073),and the Fundamental Research Funds for the Central Universities.

Das,A.;Kundu,P.(1987):Microbial production of gluconic acid.J.Sci.Ind.Res.,vol.46,pp.307-331.

Dong,Y.;Fan,Q.;Yan,X.;Guo,M.;Lu,F.(2014):Development of a hybrid model for sodium gluconate fermentation by Aspergillus niger.J.Chem.Technol.Biot.,vol.89,pp.1875-1882.

Feng,J.;Zhang,J.;Jia,W.;Yang,Y.;Liu,F.;Lin,C.(2014):An unstructured kinetic model for the improvement of triterpenes production by Ganoderma lucidum G0119 based on nitrogen source effect.Biotechnol.Bioproc.Eng.,vol.19,pp.727-732.

Gianoli,S.I.;Puxty,G.;Fisher,U.;Maeder,M.;Hungerb uhler,K.(2007):Empirical kinetic modeling of on line simultaneous infrared and calorimetric measurement using a Pareto optimal approach and multi-objective genetic algorithm.Chemometr.Intell.Lab.,vol.85,pp.47-62.

Jang,J.;Barford,J.P.(2000):An unstructured kinetic model of macromolecular metabolism in batch and fed-batch cultures of hybridoma cells producing monoclonal antibody.Biochem.Eng.J.,vol.4,pp.153-168.

Liu,J.;Weng,L.;Zhang,Q.;Xu,H.;Ji,L.(2003):A mathematical model for gluconic acid fermentation by Aspergillus niger.Biochem.Eng.J.,vol.14,pp.137-141.

Luedeking,R.;Piret,E.L.(1959):A kinetic study of the lactic acid fermentation.Batch process at controlled pH.J.Biochem.Microbiol.Technol.Eng.,vol.1,pp.393-412.

Milsom,P.;Merers,J.(1985):Gluconic&Itaconic acids,Comprehensive Biotechnology,vol.4,M.Moo-Young(ed.),pp.631-700.

Monod,J.(1949):The growth of bacterial cultures.Annu.Rev.Microbiol.,vol.3,pp.371-394.

Mustafa,I.H.;Elkamel,A.;Lohi,A.;Ibrahim,G.;Elnashaie,S.S.E.H.(2014):Structured mathematical modeling,bifurcation,and simulation for the bioethanol fermentation process using Zymomonas mobilis.Ind.Eng.Chem.Res.,vol.53,pp.5954-5972.

Praveen,C.;Sinha,S.(2009):Strategic Estimation of Kinetic Parameters in VGO Cracking.CMC-Computers Materials&Continua,vol.9,pp.41-50.

Salmi,T.;Murzin,D.Y.;M aki-Arvela,P.;Kusema,B.;Holmbom,B.;Willf or,S.;W arnå J.(2014):Kinetic modeling of hemicellulose hydrolysis in the presence of homogeneous and heterogeneous catalysts.AIChE J.,vol.60,pp.1066-1077.

Sawyer,D.T.(1964).Metal-gluconate complexes.Chem.Rev.,vol.64,pp.633-643.

Schill,N.;Van Gulik,W.;Voisard,D.;Von Stockar,U.(1996):Continuous cultures limited by a gaseous substrate:development of a simple,unstructured mathematical model and experimental verification with Methanobacterium ther-moautotrophicum.Biotechnol.Bioeng.,vol.51,pp.645-658.

Singh,O.V.;Kumar,R.(2007):Biotechnological production of gluconic acid:future implications.Appl.Microbiol.Biot.,vol.75,pp.713-722.

Takamatsu,T.;Shioya,S.;Furuya,T.(1981):Mathematical model of gluconic acid fermentation by Aspergillus niger.J.Chem.Technol.Biot.,vol.31,pp.697-704.

Zhang,B.;Yang,C.;Zhu,H.;Li,Y.;Gui,W.(2013):Kinetic Modeling and Parameter Estimation for Competing Reactions in Copper Removal Process from Zinc Sulfate Solution.Ind.Eng.Chem.Res.,vol.52,pp.17074-17086.

Znad,H.;Blazej,M.;Bales,V.;Markos,J.(2004):A kinetic model for gluconic acid production by Aspergillus niger.Chem.Pap.,vol.58,pp.23-28.

Znad,H.;Markoš J.;Baleš V.(2004):Production of gluconic acid from glucose by Aspergillus niger:growth and non-growth conditions.Process Biochem.,vol.39,pp.1341-1345.

1Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education,East China University of Science and Technology,Shanghai 200237,P.R.China

2Corresponding author:Prof.Xuefeng Yan

Email address:xfyan@ecust.edu.cn

Address:P.O.BOX 293,MeiLong Road 130,Shanghai,200237,P.R.China

Tel/Fax:+86 21 64251036

3State Key Laboratory of Bioreactor Engineering, East China University of Science and Technology,Shanghai 200237,P.R.China