栅栏效应在连续周期信号谱分析中的研究

卢梅霞 孙祥娥

摘要：离散傅里叶变换是计算机对信号频谱进行分析的理论基础，在《数字信号处理》这门课程中进行了详细的理论推导。学生在对这部分内容做实验的过程中，往往会忽视实验结果里面出现的一些由栅栏效应引起的细小差别。本文重点阐述连续周期信号频谱由栅栏效应导致的误差并提出相应的改善方法。文章还结合了实际的例子在MATLAB环境下进行了分析和验证。

关键词：栅栏效应；周期信号；DFT；谱分析

中图分类号：TN911 文献标识码：A 文章编号：1009-3044（2015）26-0196-03

Study on the Effect of Fence in the Signal Spectrum Analysis of Continuous Cycle

LU Mei-xia， SUN Xiang-e*

（Yangtze University ，College of Electronic and Information， Jingzhou 434100， China）

Abstract： Discrete Fourier Transform （DFT） is the theoretical basis for the analysis of the signal spectrum， with the theory derived in detail in the course of Digital Signal Processing. Students tend to ignore some minor differences caused by the fence effect in experimental results when conducting the experiment. This paper mainly elaborates on the error caused by the fence effect in the periodic signal spectrum analysis and the corresponding improving methods are proposed. Practical examples are also combined to be analyzed and verified in the MATLAB environment.

Key words： fence effect； periodic signal； DFT； spectral analysis

DFT是一种时域和频域均离散化的傅里叶变换，为计算机处理信号提供了理论支撑。对自然界中的连续信号进行频谱分析时，需要进行离散化和时间域的截取，再进行离散傅里叶变换得到信号的频谱。这样的信号频谱只是实际频谱的近似，因此在对连续信号进行谱分析时就有必要去采取一些措施来减小这种近似带来的影响。本文主要针对大家容易忽视的误差原因—栅栏效应作深入地探究，解决连续信号谱分析过程中容易产生疑问的地方。

在对离散周期信号做频谱分析时，对信号的截取不当会使得频谱中出现多余的频率值，下图是对单频率信号 [x（t）=cos（2πt/8）]（周期为8s，则频率[f]=1/8）作采样频率为[fs]=2[Hz]的DFT，在结果图中出现了多个频率值，针对这种现象本文从理论上作了推导，并通过例子进行了深入的分析。

1 连续信号谱分析的基本原理

利用数字的方法对连续信号进行谱分析，需要信号在时间域和频率域都是离散信号或者数字信号。对连续信号[x（t）]进行等间隔采样能够得到时间域的数字信号[x（n）]，对[x（n）]进行傅里叶变换能够得到信号的频谱[X（ejω）]：

[X（ejω）=n=-∞∞x（n）e-jωn][2] （1）

[X（ejω）]是周期为[2π]的连续函数。对[X（ejω）]进行离散化，得到频域的数字信号[X（k）]：

[X（k）=X（ejω）ω=2πNk] （2）

在进行连续信号的频谱分析时，我们是以[X（k）]来表示待分析连续信号[x（t）]的频谱[X（ejω）]。时域采样定理指出了由离散时间信号恢复连续信号的条件，频率采样定理指出了由离散频域信号恢复离散时间信号的条件。在满足这两个采样定理条件的前提下，离散化后得到的[X（k）]是否一定能够正确反映连续信号的频谱是本文需要讨论的问题。

2 连续周期信号的谱分析

设单一频率为[f0]的连续周期信号，周期[T=1/f0]，截断后信号的时域长度为[Tp]，采样时间间隔为[Ts]，则采样频率[fs=1/Ts]，采样点数[N=TP/TS]。频谱分析中的频谱分辨率F为：

[F=fs/N=1/TP] （3）

设截取时长内有[m]个周期，即

[Tp=m?T] [Tp=m?T=mf0] （4）

其中[m]为任意数。将式（3）带入式（4），可得：

[f0=fs?m/N=m?F] （5）

由于频谱分辨率F表示两条谱线所表示的频率间隔，所以只有当[m]为整数时，信号原有频率[f0]才会落在谱线上，即在时间域上对信号采用整周期截取。如果[m]不为整数时，频率[f0]落在两谱线之间，只能用相邻的谱线来近似，因此谱分析结果只能是信号频率的近似。含有多个频率成分时的推导类似。

因此对周期信号进行谱分析时，确保截取信号中含有整数个周期信号，才能获得对该连续信号频谱成分的准确分析。

3 实例分析[3]

分析正弦信号[x（t）=sin（πt/6）+cos（πt/3）]的频谱。信号包含两个频率成分[f1]=1/12，[f2]=1/6，信号的周期为12s.设采样间隔[T]=0.5s，则采样频率[fs]=2[Hz]。分别对该正弦信号截取18s、24s和54s进行信号的频谱分析。

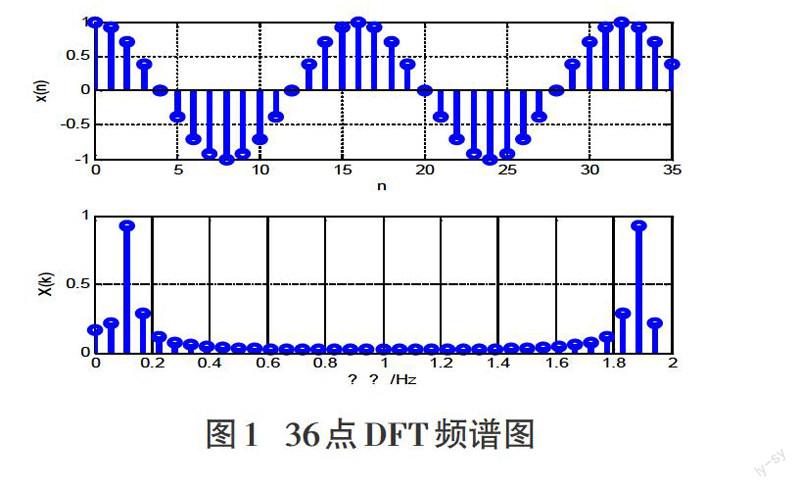
a.时间域截取18s，具有1.5个周期，采样点数[N]=36

分析：图2中截取的是1.5个周期，得到的频谱与实际频谱相比，误差较大，原始信号只有两个频率分别为1/12Hz和1/6Hz，而此频谱中出现了多个频率成分，这样使得无法区分出原始信号中真正的频率成分。

b.时间域截取24s，具有2个周期，采样点数[N]=48

分析：图3中截取两个周期，得到的频谱与实际频谱相比较没有误差，很好地反映了真实的频谱。

c.时间域截取78s，具有6.5个周期，采样点数[N]=156

分析：图4截取的是4.5个周期，得到的频谱与实际频谱相比，有误差，得到的频谱在无信号的地方出现了频率成分，但是能够区分出原始信号中的真正的频率。

小结：图2与图3相比较，整周期截取可以精确的得到真实的频谱。图2与图4相比较，在非整周期截取的情况下，增加截取的长度可以减小由于非整周期截取所带来的栅栏效应。提高频谱分析的精确度。图3与图4相比较，整周期截取比增加采样长度后的非整周期截取得到的频谱更精确。所以，对周期信号截取时，应该以整周期截取。

但是图2、图3、图4三个图中都不是从过零点开始截取的，那么对于信号从过零点开始截取对信号频谱会有怎样的影响，这将在下面讨论。

4 周期信号是否过零点采样的讨论

分析：图5中a，b采用整周期截取时，是否过零点采样对得到的频谱没有影响。c，d采用非整周期截取时，过零点采样与非过零点采样得到的频谱有差别。所以，对于连续的周期信号应该对信号进行整周期截取。如果周期不可知，应该尽量增大截取长度和采用过零点采样。

5 连续周期信号的频域恢复分析

连续的周期信号[x（n）]经过非整周期截取后，在满足时间域采样定理的条件下，其DFT得到的[X（k）]能否恢复序列[x（n）]需要做进一步的分析。

对[X（k）]进行IDFT得到

[xN（n）=IDFT[（XN（k））]N=[r=-∞+∞x（n+rN）]RN（n）] [1] [r]为整数

则在满足频率域采样定理的条件下，[xN（n）]是截断后的序列以采样点数[N]为周期的周期延拓，此时[xN（n）≠x（n）]。

正弦信号[x（t）=sin（πt/6）+cos（πt/3）]包含两个频率成分f1=1/12，f2=1/6，信号的周期为12s.设采样间隔[T]=0.5s，则采样频率[fs]=2[Hz]。一个周期内包含的采样点数为24.现截取18s的信号，具有1.5个周期，采样点数[N]=36，对其先做DFT后再做IDFT，得到[xN（n）]。

分析：图6中的下图一个周期内的采样点数是36，周期为18s，与[x（n）]的周期相比周期发生了改变，不再是原来的12s。因此对连续的周期信号进行非整周期截取后，做DFT得到的频域信号不能恢复连续的周期信号，这也解释了非整周期截取得到的频谱与真实的频谱有较大误差的原因。

6 结束语

栅栏效应很难克服，有时候甚至会引起严重的误差，同时根据不同的信号特点所采用的减小栅栏效应方法的有效性也不同，所以找到信号的基本特性对我们得到误差较小的频谱是非常有帮助的。对于周期信号能有效地改善栅栏效应的方法就是整周期截取且过零点采样。对于周期未知的信号需要增大DFT点数来改善栅栏效应[4-5]。

参考文献：

[1] 李永全，杨顺辽，孙祥娥.数字信号处理[M].武汉：华中科技大学出版社，2011：75.

[2] 胡广书.数字信号处理（理论、算法与实现）[M].北京：清华大学出版社，2003：100.

[3] 林爱英，滕红丽，袁超，等.DFT在信号谱分析中的应用[J].安徽工业大学学报，2011，28 （2）：192-195.

[4] 张登奇，杨慧银.信号的频谱分析及MATLAB 实现[J].湖南理工学院学报：自然科学版，2010，23（3）：29-33.

[5] 乔建华，张雪英.用DFT 对连续信号谱分析的误差问题[J].现代电子技术，2014，37（13）：53-56.