某型500 MW汽轮机组中压转子的高温蠕变强度分析

徐亚涛，张 磊，张俊杰

（神华国华（北京）电力研究院有限公司，北京 100025）

0 引言

汽轮机轴系振动关系到机组安全稳定运行，转子弯曲是各种转子常见且较难消除的振动故障之一。根据国内外轴系破坏事故的统计显示[1]，汽轮机轴系破坏主要原因之一是在运行中突然产生转子弯曲导致过大不平衡引起的。影响转子弯曲的因素很多，包括材质、设计、运行等。其中长期高温服役过程中产生的蠕变变形是导致转子发生永久塑性弯曲的主要原因。因此，非常有必要就转子蠕变变形对机组安全性的影响进行深入研究，避免产生轴系破坏的严重后果。

本文针对某型500 MW超临界汽轮机组，选取机组实际运行中发生振动最大的中压转子，利用有限元技术进行了该转子在不同不平衡力作用下的蠕变弯曲计算分析，并结合机组实际运行检修情况分析蠕变弯曲对安全性的影响。所研究的2台某型500 MW超临界汽轮发电机组中压转子均在第2次A级检修中发现转子弯曲严重超标，并都进行了直轴处理。同类机组的调研也发现了中压转子在机组投运一段时间后普遍存在着不同程度的弯曲。因此，本研究的目的是通过中压转子蠕变变形的计算研究，分析不同不平衡力下蠕变变形对转子弯曲的影响，为提出有效的抗蠕变措施提供依据。

1 转子有限元模型

由于实际的转子模型结构复杂，细微结构众多，不可能完全建模分析，需要对其进行一定的简化处理。本文以简化处理对计算结果影响较小作为忽略原则，进行了以下处理。

a）由于各级轮盘气动载荷及转子自身重力对转子的静强度影响很小，本文忽略了转子自身重力及轴向气流力的影响，只考虑转子离心力、温度载荷及不平衡离心力。

b）由于实际叶片模型众多且复杂，相关因素众多，无法完全建模，因而将转子轮盘计算外半径取为轮盘的实际外径进行处理。

c）简化对计算结果影响很小的圆角等细小结构。

d）为了较好地模拟轴承对转子弯曲变形的约束作用，左右两端取为轴承的轴向中分面，即忽略了轴承轴向上中分面以外的转子结构。

为了保证结果准确，采用了足够精密的网格，整个转子的单元数为162 729，节点数为720 800，有限元模型如图1所示。

图1 转子模型示意图及其有限元模型

中压转子的左右端面和中心孔表面均设为绝热边界条件。在中压转子两端通过采用一种特殊的点—面接触方式来模拟，其中接触单元分别为TARGE170及CONTACT175。约束了左端控制节点的UX、UY、UZ、ROTY、ROTZ自由度，约束右端控制节点的UX、UY、ROTY、ROTZ自由度[2]。

2 确定蠕变模型

由于500 MW机组中压转子长期工作在高温工况下，蠕变初始阶段的变形量相对于转子在长时间工作后的蠕变变形量很小，可以忽略[3]，因而可以认为转子弯曲主要由蠕变变形第二阶段控制。在ANSYS中常用的隐式第二阶段蠕变模型有：指数形式蠕变模型ε˙=和 Norton 蠕变模型ε˙=

某型500 MW机组中压转子的材质是P2MA钢。表1中给出了P2MA钢在不同温度和不同应力水平下的蠕变性能数据。

表1 P2MA钢的蠕变极限和持久强度[4]

根据表1中的数据，采用Matlab的多元线性回归拟合分析，就得到了Norton蠕变模型的各个系数：C1=1.82×10-28，C2=5.379 8，C3=45 458.54。

由于材料的热处理及材料成分不同，材料的蠕变特性规律也不同，虽然Norton模型或指数形式的蠕变模型能对通用的许多材料有较好地吻合，但是对于P2MA钢的材料数据及分析可知，无论是Norton模型还是指数形式的蠕变模型都不能很好地吻合所有的实验数据，对于Norton模型在高温时，所得到的Norton模型能较好地描述材料的实验数据，而温度越低，其呈现偏差越大的趋势，即在低温区域，通过Norton模型计算得到的蠕变速率要低于实验数据。而对于指数形式的蠕变模型，在高温区，蠕变模型计算得到的蠕变速率要低于实验数据，而在低温区计算得到的蠕变数据又要高于实验数据。综合考虑实际转子的蠕变弯曲主要是由于高温区域的蠕变所造成的结果，最后选择采用Norton蠕变模型作为后续中压转子蠕变弯曲分析模型[5]。

3 中压转子的温度场分布和应力场分布

图2给出了中压转子温度场有限元分析结果。可以看出，转子的温度场分布均匀，基本上是关于转子的中分面对称分布，并从中间进汽部分沿轴线向两端逐渐降低，在转子的径向及周向，温度变化很小。在转子的中部表面温度最高，其温度值接近进汽温度，最大温度值达539℃，而在两端轴颈处温度最低，约为80℃。

图2 中压转子的稳态温度场分布图（竖直剖分视），℃

4 转子的蠕变弯曲计算

4.1 蠕变计算及说明

根据转子的检修情况，取蠕变计算时间为76 718.86 h，设置基准时间步间隔为300 h；在ANSYS中分两步加载，第一步设置终止时间为1×108，主要是加载离心力、温度及不平衡离心力，不考虑蠕变；第二步设置终止时间为76 718.86，将蠕变开关打开。将转子中截面底部的节点Node224332作为参考点，提取其Y向相对位移的计算结果作为转子的蠕变弯曲计算值。

由于实际转子不平衡量的大小很难准确获取，为明确不平衡量对转子蠕变弯曲量的影响，本文分别计算了两种不同偏心距工况，即偏心距为8μm、16μm。

4.2 中压转子蠕变弯曲有限元分析结果

从图3可以看出，转子在经过了76 718.86 h蠕变变形后，转子的等效应力基本不变，其最大值仍为蠕变开始时刻的应力值，仅是在转子中段的等效应力值有所变化，这主要是因为该中压转子中部存在高温区，从而中部发生蠕变变形，而转子的大部分区域基本没有受到蠕变的影响，转子的等效应力在整个蠕变过程中基本不变；偏心距对转子的最大等效应力及等效应力分布影响很小，其主要作用体现在对中间轴段的等效应力及对蠕变速率的影响，从而对转子的蠕变弯曲量产生影响。从蠕变后应力分析，不同偏心距的蠕变规律是一致的，即转子大部分区域的等效应力都没有得到松弛。

图3 转子蠕变弯曲后的等效应力分布图（竖直剖分视），Pa

另外，不同偏心距下的等效蠕变反映了转子服役过程中蠕变变形的情况。在整个蠕变过程中，蠕变主要是发生在中压转子中部，即高温区域，而转子的大部分区域蠕变变形量很小。此外还发现了偏心距的不同并没有影响转子的蠕变变形区域，偏心距主要是对转子的蠕变弯曲量有影响。

转子蠕变过程中，节点的总位移量包括了弹性变形、热膨胀量及蠕变变形量，因而参考点在某个方向上的蠕变变形量是该点在该方向上的相对位移量，即在某一方向上终止时刻该点的位移减去初始时刻该点的位移。

图4 不同偏心距下转子参考点的Y向位移随时间的变化曲线

检修过程中测量得到的中压转子永久弯曲量为0.15 mm，在计算得到的结果范围内。从图3还可以发现，虽然偏心距大小对蠕变变形区域影响不大，但对转子的弯曲量具有重要影响。

为了清晰地观察不同偏心距对蠕变弯曲量的影响，图5给出了转子的蠕变弯曲量随偏心距的变化关系曲线，可以看出弯曲变形量和偏心距成线性关系，转子弯曲量随着偏心距的增大而增大。

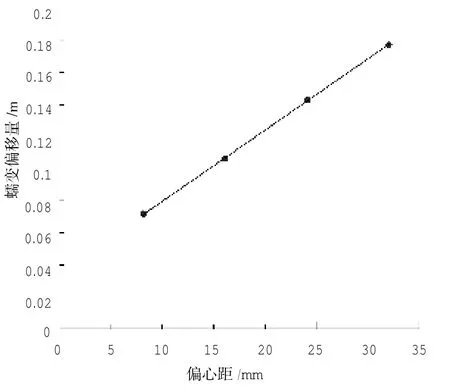
图5 参考点的蠕变弯曲量随偏心距的变化曲线

综上所知，不同偏心距对转子蠕变的主要发生区域及转子等效应力分布影响很小，主要是影响高温区域的蠕变变形量，转子的蠕变弯曲量与偏心距呈近似线性关系，偏心距越大则转子蠕变弯曲量越大，可以通过图5的关系曲线来估算不同偏心距下的转子蠕变弯曲量，从而对中压转子的蠕变弯曲进行预测。

5 结束语

本文针对某型500 MW汽轮机机组实际运行中发生振动最大的中压转子，利用有限元分析方法研究了在不同偏心距工况下，转子的温度分布、应力分布以及蠕变变形情况,得出以下结论。

a）中压转子的温度场分布基本是关于转子的轴向中分面对称，温度沿径向及周向变化很小，沿轴向温度逐渐降低，轴向温度梯度较大，且在转子中部存在高温区，最大温度达539℃。

b）通过两种不同偏心距工况下的综合加载等效应力计算结果知，在该两种工况下，综合加载等效应力的分布基本一致，最大等效应力出现在最后级轮盘的中心孔处，不平衡离心力载荷相对离心力载荷及温度载荷较小，对转子等效应力场的影响很小。

c）不同不平衡离心力对转子的应力场影响较小，但对蠕变弯曲量影响较大；随着偏心距的增大，蠕变弯曲量与偏心距基本呈线性变化，转子的蠕变主要发生在中压转子中部高温区域，转子其他大部分区域的蠕变变形量相对较小。

d）在偏心距为8～32μm的工况下，500 MW机组中压转子的蠕变弯曲量在0.071～0.177 mm范围内，检修过程中测量得到的中压转子永久弯曲量为0.15 mm，在计算得到的结果范围内。

[1] Adams，Maurice L.．Large Unbalance Vibration Analysis of Steam TurbineGenerators[M]．Electric Power Research Institute，1984：25.

[2]姜求志，王金瑞．火力发电厂金属材料手册[M].北京：中国电力出版社，2000:644-645.

[3]闯邦椿，顾家柳，夏松波，等.高等转子动力学理论、技术与应用[M].北京：机械工业出版社，2000：30.

[4]陆颂元.汽轮发电机组大不平衡状态下非线性振动特性研究[J]．中国电机工程学报，1995,15(6)：391-396.

[5] 施维新.转子大不平衡引起轴系破坏机理的研究[J]．河北电力技术，1992(5)：18-24.