CFRP—方钢管混凝土轴压短柱承载力分析

赵均海+杜文超+张常光

摘要：采用统一强度理论对CFRP-方钢管混凝土轴压短柱进行受力分析，并引入等效应力系数、混凝土强度折减系数和等效约束折减系数，将CFRP-方钢管混凝土转化为CFRP-圆钢管混凝土，进而建立了CFRP-方钢管混凝土轴压短柱的极限承载力计算公式。将所得理论公式的计算结果与文献资料数据进行对比，验证了该公式的正确性，并进行了影响因素分析。结果表明：随材料拉压比、统一强度理论参数和CFRP厚度的增加，CFRP-方钢管混凝土轴压短柱的极限承载力不断增大，但CFRP的约束效率却随其厚度的增加在减小；所得结论可为CFRP-方钢管混凝土轴压短柱的设计、施工及推广提供一定的理论依据。

关键词：统一强度理论；碳纤维增强复合材料；方钢管混凝土；轴压短柱；极限承载力

中图分类号：TU375.3 文献标志码：A

0 引 言

钢管混凝土因具有三向受压混凝土抗压强度高的优点而越来越广泛地被应用于工业厂房、桥梁结构和超高层建筑结构中，取得了很好的力学及经济效果，虽然方钢管混凝土较截面面积和含钢率相同的圆钢管混凝土承载力有所降低[1]，但因其具有节点构造简单，便于梁柱连接，施工方便等优点[2]，在实际工程中得到了广泛的应用。混凝土的存在可以消除钢管的内凹，却不能避免其外凸，而且实际工程中还会遇到方钢管混凝土轻微受损或需要增加新功能的情况，这些都涉及到采取某种措施对方钢管混凝土进行约束、加固或修复的问题。近年来，碳纤维增强复合材料（CFRP）外包结构构件加固技术在各国已进行了大量的研究[3-4]，其优良的加固效果和便捷的施工工艺越来越多地受到人们的重视。由此出现的CFRP-圆钢管混凝土已经成为一个研究热点[5-6]，参照CFRP-圆钢管混凝土，笔者在方形钢管混凝土的外壁包裹CFRP以进一步改善其受力性能。利用CFRP约束钢管混凝土不仅提高了钢管混凝土的承载力、有效延缓了钢管的局部屈曲，且弥补了CFRP约束钢筋混凝土的延性不足[2]，考虑到CFRP直接粘贴在方柱（未经任何倒角）上的约束效果不理想[7]，因此本文研究对象为带倒圆角截面形式的CFRP-方钢管混凝土柱。目前关于CFRP-方钢管混凝土的研究相对较少，且主要为试验研究和数值模拟，王庆利等[2]对CFRP-方钢管混凝土轴压短柱进行了试验研究和有限元模拟，并提出了受约束混凝土的应力-应变表达式，刘洋[8]对CFRP-方钢管混凝土柱的压弯性能进行了试验研究，并分析了CFRP厚度、长细比和偏心率的大小等因素对承载力的影响，Choi等[9]提出一个简化模型分析不同参数下外贴CFRP对钢管混凝土的加强，Sundarraja等[10]研究了用条状CFRP加固方钢管混凝土轴压短柱的力学性能，并用钢管和混凝土各自承载力进行简单的叠加，不能真实反映钢管和混凝土的受力特性。本文充分考虑中间主应力的影响，根据统一强度理论与CFRP-方钢管混凝土的材料特点，引入了考虑厚度比ζ（ζ=tf/ts，tf为CFRP层厚度，对于采用CFRP条间隔粘贴加固的情况tf取其满铺时的平均厚度，ts为方钢管壁厚）影响的等效应力系数ξ，将方CFRP筒对内部钢管混凝土的约束等效为圆CFRP筒对钢管混凝土的约束。同时引入混凝土强度折减系数[11]和等效约束折减系数[12]，将内部方钢管混凝土轴压短柱等效为圆钢管混凝土轴压短柱，进而推导出CFRP-方钢管混凝土轴压短柱的极限承载力公式，与文献试验数据进行比较验证，并得出各参数对极限承载力的影响特性。

1 统一强度理论

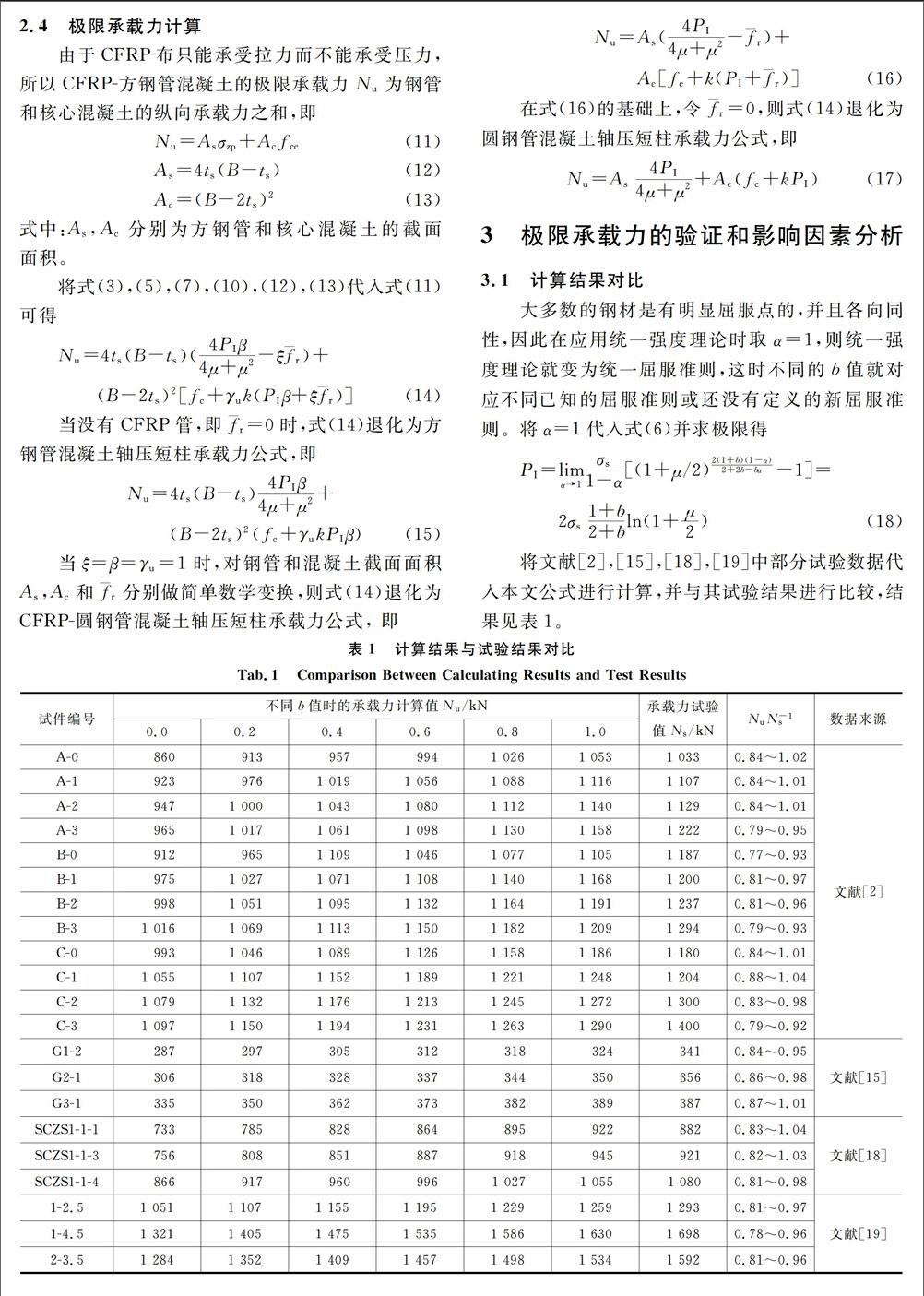
统一强度理论是俞茂宏在双剪强度理论的基础上建立的一种考虑了中间主应力影响的计算准则，该理论采用一个统一的力学模型，可以十分灵活地适用于各种不同特性的材料，其表达式为[13]

F=σ1-α1+b（bσ2+σ3）=σs σ2≤σ1+ασ31+α

F′=11+b（σ1+bσ2）-ασ3=σs σ2≥σ1+ασ31+α

α=σsσc，b=（1+α）τs-σsσs-τs

（1）

式中：F，F′均为主应力强度理论函数；σ1，σ2，σ3为最大主应力、中间主应力和最小主应力；σs，σc，τs分别为材料的拉伸、压缩、剪切屈服强度；α为材料的拉压比，对于韧性金属材料一般为0.77～1.0，对于脆性金属材料为0.33～0.77，对于岩土类材料一般小于0.5；b为反映中间剪应力以及相应面上的正应力对材料破坏影响程度的参数，0≤b≤1。2 极限承载力分析

2.1 CFRP受力分析

CFRP-方钢管混凝土柱在轴向压力作用下，钢管混凝土的横向膨胀使CFRP布的水平段产生水平弯曲，并对方钢管混凝土提供约束力。另外，在方形截面的角部，CFRP布受到2个相互垂直方向的拉力作用，其合力形成对方钢管混凝土对角线方向的强约束，故方钢管混凝土承受的约束力是沿对角线的集中挤压力和沿边长分布均匀的横向力[14]。本文引入考虑厚度比ζ影响的等效应力系数ξ，将方CFRP筒对内部钢管混凝土的约束等效为圆CFRP筒对钢管混凝土的约束，并采用等效约束力frf来简化计算，计算简图如图1所示，其中B为方钢管的外边长，σr为混凝土所受的侧向压力，ff为CFRP应力，其原理是使简化后的均匀约束分布与原来的非均匀约束具有相同的约束效果。对文献[10]中的试验数据进行拟合（图2），得等效应力系数ξ与厚度比ζ的表达式为

对于采用CFRP条间隔粘贴加固的情况，由于CFRP粘贴的不均匀，可采用安全系数Fs=1.2对ξ进行折减[10]。

等效约束力frf的计算公式如下

frf=ξr

（3）

式中：r为平均约束应力，r=2tfff/B。

2.2 方钢管受力分析

CFRP-方钢管混凝土向CFRP-圆钢管混凝土面积相等转换时，由于方钢管对混凝土约束的不均匀，使得这种等代有困难。本文引入等效约束折减系数β [12]将方钢管对混凝土的约束转换为圆钢管对混凝土的约束，其值为

β=66.474 1v2-0.991 9v+0.416 18

（4）

式中：v为钢管的厚边比，v=ts/B。

方钢管对核心混凝土的等效均匀径向压力P可表示为

P=βPI

（5）

式中：PI为等效外圆钢管在径向压力作用下的塑性极限荷载。

根据统一强度理论，PI值为[15]

PI=σs1-α[（rcrc+ts）2（1+b）（α-1）2+2b-bα-1]=

σs1-α[（1+μ/2）2（1+b）（1-α）2+2b-bα-1]

（6）

式中：μ为含钢率；rc为等效圆钢管的内壁半径，rc=（B-2ts）/π。

由塑性力学的厚壁圆筒理论得[16]等效外圆钢管的纵向抗压强度σzp为

σzp=4（P+frf）r2c-frf（rc+ts）2（rc+ts）2-r2c=

4PIβ4μ+μ2-frf

（7）

2.3 核心混凝土的轴压强度

CFRP-方钢管混合筒对核心混凝土的约束分布很不均匀，角部混凝土受到的约束较强，边部中间管壁受到的约束作用较弱。根据Varma等[17]的研究，核心混凝土所受的约束可分为有效约束区和非有效约束区，分界线为抛物线，其约束模型见图3，其中，re为等效圆钢管的外壁半径，re=B/π。有效约束区混凝土2个方向的约束力相近，其应力状态与CFRP-圆钢管混凝土中的核心混凝土相似，而非有效约束区，垂直于表面的约束较小。

核心混凝土处于三向受压状态，0>σ1=σ2>σ3，满足式（1），代入得

σ1-ασ3=ft

（8）

式中：ft为混凝土抗拉强度，ft=2ccos（φ）1+sin（φ），φ为混凝土的内摩擦角，c为混凝土的内聚力。

令k=1+sin（φ）1-sin（φ），并按习惯一般取压为正、拉为负，得

σ3=fc+kσ1

（9）

式中：σ1=P+frf；fc为核心混凝土的单轴抗压强度，fc=2ccos（φ）1-sin（φ）。

鉴于CFRP-方钢管混合筒对核心混凝土的约束存在一定的困难，现有CFRP-方钢管混凝土的研究多是建立在试验基础上的。本文对核心混凝土不做有效约束区和非有效约束区的划分，而采用混凝土强度折减系数[11]γu=1.67D-0.112c来考虑非有效约束区侧向约束减弱的影响，其中Dc为等效圆钢管的内径。核心混凝土的纵向抗压强度fcc为

fcc=fc+γuk（P+frf）

（10）

2.4 极限承载力计算

由于CFRP布只能承受拉力而不能承受压力，所以CFRP-方钢管混凝土的极限承载力Nu为钢管和核心混凝土的纵向承载力之和，即

Nu=Asσzp+Acfcc

（11）

As=4ts（B-ts）

（12）

Ac=（B-2ts）2

（13）

式中：As，Ac分别为方钢管和核心混凝土的截面面积。

将式（3），（5），（7），（10），（12），（13）代入式（11）可得

Nu=4ts（B-ts）（4PIβ4μ+μ2-ξr）+

（B-2ts）2[fc+γuk（PIβ+ξr）]

（14）

当没有CFRP管，即r=0时，式（14）退化为方钢管混凝土轴压短柱承载力公式，即

Nu=4ts（B-ts）4PIβ4μ+μ2+

（B-2ts）2（fc+γukPIβ）

（15）

当ξ=β=γu=1时，对钢管和混凝土截面面积As，Ac和r分别做简单数学变换，则式（14）退化为CFRP-圆钢管混凝土轴压短柱承载力公式， 即

Nu=As（4PI4μ+μ2-r）+

Ac[fc+k（PI+r）]

（16）

在式（16）的基础上，令r=0，则式（14）退化为圆钢管混凝土轴压短柱承载力公式，即

Nu=As4PI4μ+μ2+Ac（fc+kPI）

（17）3 极限承载力的验证和影响因素分析

3.1 计算结果对比

大多数的钢材是有明显屈服点的，并且各向同性，因此在应用统一强度理论时取α=1，则统一强度理论就变为统一屈服准则，这时不同的b值就对应不同已知的屈服准则或还没有定义的新屈服准则。将α=1代入式（6）并求极限得

PI=limα→1σs1-α[（1+μ/2）2（1+b）（1-α）2+2b-bα-1]=

2σs1+b2+bln（1+μ2）

（18）

将文献[2]，[15]，[18]，[19]中部分试验数据代入本文公式进行计算，并与其试验结果进行比较，结果见表1。

从表1可以看出，本文理论计算结果与试验结果吻合良好，验证了该理论公式的正确性，并且极限承载力Nu随着b的增加而增大，说明考虑参数b即中间剪应力以及相应面上的正应力对材料破坏的影响，可以更充分地发挥材料的强度潜能。当b=1时，统一强度理论退化为双剪应力屈服准则，这时本文计算值与试验值比值的平均值为0.981，方差为0.001，表明本文公式计算结果具有较高的精度。

3.2 影响因素分析

对于高强钢材，材料拉压比α将不再等于1。图4给出了试件B-1的极限承载力Nu随α，b的变化情况。从图4可以看出：当α一定时，Nu随着b的增加而增大；当b一定时，Nu随着α的增加而增大，说明当外钢管为高强度钢时考虑α的影响是有必要的。

对文献[2]中的数据进行分析，得出极限承载力Nu与CFRP粘贴层数、fc之间的关系，如图5所示。从图5可以看出，极限承载力Nu随着fc的增加而增加，且承载力的提高幅度取决于CFRP的厚度。粘贴1层时极限承载力平均提高63 kN，粘贴2层时极限承载力平均提高87 kN，粘贴3层时极限承载力平均提高105 kN，说明CFRP的约束效率随其厚度的增加而减

fc钢管厚边比v反映的是钢管的厚度和外边长的比值，厚边比不同会影响钢管对内部核心混凝土的约束，图6给出了文献[2]中试件A-1和B-1在其余条件均不变的情况下极限承载力Nu随厚边比v的变化情况。从图6可以看出，极限承载力Nu随着厚边比v的增大而显著增大，说明在构件外边长、CFRP和内部混凝土不变的情况下增大钢管的壁厚能显著提高构件的承载力。

4 结 语

（1）本文在统一强度理论的基础上推导出了CFRP-方钢管混凝土轴压短柱极限承载力的计算公式，并将理论计算结果与相关文献的试验结果做比较，验证了该公式的正确性，同时也说明了将CFRP-方钢管混凝土转化为CFRP-圆钢管混凝土的思路是可行的。

（2）CFRP-方钢管混凝土轴压短柱的极限承载力Nu随着α和b的增加而增大，说明考虑材料的拉压比α和参数b的影响是有必要的。由于外围CFRP筒的约束作用，方钢管混凝土柱的承载力得到较大幅度提高，承载力提高的幅值直接取决于CFRP的厚度。当钢管边长、CFRP和混凝土一定时，增大钢管的壁厚能显著提高构件的承载力。

（3）本文公式是考虑了各种影响因素的统一解，改变公式中参数就对应了不同的边界情况，CFRP-圆钢管混凝土轴压短柱承载力、圆形和方形截面钢管混凝土轴压短柱承载力都是本文结果的特例。

参考文献：

References：

[1] 吴 鹏，赵均海，李 艳，等.方钢管混凝土短柱轴压极限承载力研究[J].四川建筑科学研究，2013，39（3）：8-13.

WU Peng，ZHAO Jun-hai，LI Yan，et al.Study on the Axial Ultimate Bearing Capacity of Square Concrete-filled Steel Tubular Stub Columns[J].Sichuan Building Science，2013，39（3）：8-13.

[2]王庆利，薛 阳，邵永波，等.CFRP约束方钢管混凝土轴压短柱的静力性能研究[J].土木工程学报，2011，44（3）：24-31.

WANG Qing-li，XUE Yang，SHAO Yong-bo，et al.Study of Static Performance of Axially Compressed Concrete Filled Square Steel Tubular Stub Columns Confined by CFRP[J].China Civil Engineering Journal，2011，44（3）：24-31.

[3]MEIER U.Carbon Fiber Reinforced Polymer：Modern Materials in Bridge Engineering[J].Structural Engineering International，1982（2）：7-12.

[4] SHANMUGANATHAN S.Fiber Reinforced Polymer Composite Material for Civil and Building Structural Review of the State-of-art[J].The Structural Engineering，2003（7）：26-33.

[5]张常光，赵均海，冯红波.CFRP-钢管混凝土轴压短柱的力学性能[J].建筑结构，2008，38（3）：34-37.

ZHANG Chang-guang，ZHAO Jun-hai，FENG Hong-bo.Mechanics Behavior of Concrete Filled CFRP-steel Tube Stub Columns Under Axial Compression[J].Building Structure，2008，38（3）：34-37.

[6]王庆利，叶 茂，周 琳.圆CFRP-钢管混凝土构件受弯性能研究[J].土木工程学报，2008，41（10）：30-38.

WANG Qing-li，YE Mao，ZHOU Lin.Study on the Flexural Behavior of Concrete Filled Circular CFRP-steel Tubular Members[J].China Civil Engineering Journal，2008，41（10）：30-38.

[7]潘景龙，王雨光，来文汇.混凝土柱截面形状对纤维包裹加固效果的影响[J].工业建筑，2001，31（6）：17-19.

PAN Jing-long，WANG Yu-guang，LAI Wen-hui.Effect of Sectional Shape of Concrete Column on the Bearing Capacity of Short Columns Wrapped with FRP[J].Industrial Construction，2001，31（6）：17-19.

[8]刘 洋.CFRP增强方钢管混凝土压弯构件静力性能研究[D].沈阳：沈阳建筑大学，2011.

LIU Yang.Static Performance Study on the Strengthened of Concrete Filled Square Steel Tubular Beam-columns by CFRP[D].Shenyang：Shenyang Jianzhu University，2011.

[9]CHOI K K，XIAO Y.Analytical Model of Circular CFRP Confined Concrete-filled Steel Tubular Columns Under Axial Compression[J].Journal of Composites for Construction，2010，14（1）：125-133.

[10]SUNDARRAJA M C，GANESH P G.Experimental Study on CFST Members Strengthened by CFRP Composites Under Compression[J].Journal of Constructional Steel Research，2012，72：75-83.

[11] KENIJ S，HIROYUKI N，SHOSUKE M，et al.Behavior of Centrally Loaded Concrete-filled Steel-tube Short Columns[J].Journal of Structural Engineering，2004，130（2）：180-188.

[12]李小伟，赵均海，朱铁栋，等.方钢管混凝土轴压短柱的力学性能[J].中国公路学报，2006，19（4）：77-81.

LI Xiao-wei，ZHAO Jun-hai，ZHU Tie-dong，et al.Mechanics Behavior of Axially Loaded Short Columns with Concrete-filled Square Steel Tube[J].China Journal of Highway and Transport，2006，19（4）：77-81.

[13]俞茂宏.混凝土强度理论及其应用[M].北京：高等教育出版社，2002.

YU Mao-hong.Concrete Strength Theory and Application[M].Beijing：Higher Education Press，2002.

[14]卢亦焱，史健勇，赵国藩.碳纤维布约束轴心受压混凝土方形柱承载力计算公式[J].工程力学，2004，21（4）：22-27.

LU Yi-yan，SHI Jian-yong，ZHAO Guo-fan.Study of Axial Bearing Capacity of Square Concrete Columns Confined with Carbon Fiber Reinforced Plastic[J].Engineering Mechanics，2004，21（4）：22-27.

[15]赵均海.强度理论及其工程应用[M].北京：科学出版社，2003.

ZHAO Jun-hai.Unified Strength Theory and Its Engineering Application[M].Beijing：Science Press，2003.

[16]王 仁，熊祝华，黄文彬.塑性力学基础[M].北京：科学出版社，1982.

WANG Ren，XIONG Zhu-hua，HUANG Wen-bin.Foundation of Plastic Mechanics[M].Beijing：Science Press，1982.

[17]VARMA A H，SAUSE R，RICLES J M，et al. Development and Validation of Fiber Model for High Strength Square Concrete Filled Steel Tube Beam-columns[J].ACI Structural Journal，2005，102（1）：73-84.

[18]韩林海，陶 忠.方钢管混凝土轴压力学性能的理论分析与试验研究[J].土木工程学报，2001，34（2）：17-25.

HAN Lin-hai，TAO Zhong.Study on Behavior of Concrete Filled Square Steel Tubes Under Axial Load[J].China Civil Engineering Journal，2001，34（2）：17-25.

[19]顾 威，赵颖华，尚东伟.CFRP-钢管混凝土轴压短柱承载力分析[J].工程力学，2006，23（1）：149-153.

GU Wei，ZHAO Ying-hua，SHANG Dong-wei.Load Carrying Capacity of Concrete Filled CFRP-steel Tubes Under Axial Compression[J].Engineering Mechanics，2006，23（1）：149-153.