列车荷载作用下铁路斜拉桥索—梁相关振动研究
2015-12-10王涛沈锐利
王涛+沈锐利


摘要:为了研究大跨度铁路斜拉桥的索-梁相关振动,基于拉索非线性振动理论,开发了有限元索动力单元,该单元在静力计算中为普通直杆单元,动力特性计算中可以计算拉索局部自振频率,动力时程计算中可以计算拉索非线性振动与整体结构振动的相互作用;编制了计算程序,建立了大跨度铁路斜拉桥有限元模型,同时使用索动力单元模拟斜拉索,最后研究了列车通过斜拉桥时梁、塔的带动下拉索发生索-梁相关振动的特性。结果表明:对于大跨度铁路斜拉桥,列车在设计速度范围内通过桥梁时索-梁相关振动不会导致拉索产生大幅振动。
关键词:斜拉桥;拉索;索-梁相关振动;有限元法;列车;荷载
中图分类号:U441.3 文献标志码:A
0 引 言
对于单根斜拉索,理论分析、数值计算与试验研究均表明当拉索端点位移激励频率与拉索自振频率达到1∶1或2∶1时,拉索容易发生较大幅度的振动[1-10]。从工程实际来看,斜拉桥是一个包含多根拉索的复杂索-梁组合结构,拉索振动的情况较为复杂。为了研究实际斜拉桥上拉索是否容易在端点位移激励的作用下发生较大幅度的振动,Gattulli等[11]于2002年使用理论方法建立了索-梁作用下振动的精细模型,使用振型分解法研究了拉索局部振动与全桥振动特性之间的关系,建立了全桥有限元模型,分析了斜拉桥在风荷载和地震荷载作用下索-梁耦合振动情况。Lorenzo等[12]于2003年进行了索-梁相互作用的振动试验研究,测试了汽车荷载通过桥梁时拉索的振动情况。Caetano等[13]于2008年使用有限元法对桥梁的振动特性进行了分析,通过对比拉索的振动频率与全桥自振频率的关系来判定拉索发生大幅振动的可能性,使用有限元法研究了在车辆荷载和风荷载激励下拉索的振动情况,并通过对实际桥梁的测试来验证数值计算的结果。Zhang等[14]于2011年使用车桥动力计算程序得到了斜拉桥拉索端点在车辆作用下的振动位移时程作为激励条件,提取端点位移时程,使用非线性有限元法分析单根斜拉索的振动响应,在其研究中忽略了拉索非线性振动对斜拉桥整体结构振动的影响。Caetano[15]于2011年在其关于拉索振动的著作中阐明:根据现有世界各地的实际斜拉桥调查研究资料,拉索大幅振动通常发生于较为恶劣的天气状况下,桥面的振动频率与拉索频率达到一定的匹配关系是造成拉索大幅振动的部分原因。
根据现有的研究资料可以发现,目前关于单根斜拉索在端点位移作用下大幅振动的研究较多,但斜拉桥全桥模型中拉索在端点位移激励作用下发生振动的研究相对较少,对于拉索与全桥振动的相互动力作用考虑还不够全面。
文献[16]中分析了索-梁组合结构中在整体结构振动的带动下拉索发生振动的本质规律,提出了索-梁相关振动的概念,其主要包括拉索上常见的强迫振动与参数振动,认为拉索有可能在索-梁相关振动的作用下发生1∶1的主共振与2∶1的参数共振。建立了包含3根拉索的索-梁组合结构计算模型,初步分析了简单索-梁组合结构发生大幅度索-梁相关振动的性质,认为当拉索发生大幅振动时,拉索局部振动与整体结构振动不能分开考虑,应当充分考虑拉索局部振动与整体结构振动之间的相互关系来分析索-梁组合结构中拉索在端点位移激励下大幅振动的现象,否则计算结果可能与实际情况有较为明显的偏差。
为了研究大跨度铁路斜拉桥在列车荷载作用下索-梁相关振动的特性,考察列车荷载作用下索-梁相关振动是否容易导致拉索的大幅振动,本文中笔者在文献[16]的基础上开发索动力单元,该单元在动力时程计算中可以计算斜拉桥拉索局部非线性振动与整体结构振动的相互作用,编制有限元程序,针对有代表性的铁路斜拉桥进行研究,本文结果可以为大跨度铁路斜拉桥的设计提供理论参考。
1 计算理论
1.1 拉索动拉力计算
图1为拉索在端点位移激励下的振动模型,其中,ΔU(t)为拉索端点位移激励,ΔUX(t),ΔUY(t)分别为ΔU(t)沿拉索局部坐标系下X,Y方向的位移分量,θ为拉索倾角,v为拉索振动曲线,y为拉索下垂曲线,t为时间。
根据拉索振动理论[1]与试验研究[10],ΔUY(t)位移激励导致拉索发生强迫振动,当频率成分与拉索自振频率接近1∶1时,拉索容易发生主共振;ΔUX(t)位移激励容易导致拉索发生参数振动,当频率成分与拉索自振频率接近2∶1时,拉索容易发生参数共振。
在实际斜拉桥上,拉索发生上述2种振动通常均是由梁、塔的带动导致的[15,17]。与文献[16]相同,本文将这种斜拉桥拉索在端点位移激励作用下发生的振动统称为索-梁相关振动。
若考虑拉索上同时发生了j(j=1,2,3,…)阶模态的大幅振动,拉索的振型函数v(x,t)为[1]
v(x,t)=ji=1Visin(iπxl)
(1)
式中:Vi为拉索振动响应函数;sin(·)为拉索的振型函数;x为拉索上某一点的位置坐标;l为拉索两端点之间的距离。
由图1中的理论模型及文献[16]的方法,可以推导得到拉索在端点位移激励作用下第n(n∈[1,j])阶振动的单自由度非线性振动方程为
n+2εωnn+ω2nVn+a1Vn+a2V2n+
a3V3n+a4+B=F
(2)
其中
ω2n=-(Hcnmen+EAdnanlemen)
a1=-EAcnmen[ΔUX(t)l0+ΔU2Y(t)2l20]
a2=-EA(2ancn+bndn)2menle
a3=-EAbncn2menle
a4=-EAdnmen[ΔUX(t)l0+ΔU2Y(t)2l20]
F=-fnenΔY(t)
B=B1+B2
B1=-EAVncnlemen[ji=1Viai-Vnan+
12(ji=1V2ibi-V2nbn)]
B2=-EAdnlemen[ji=1Viai-Vnan+
12(ji=1V2ibi-V2nbn)]
式中:H为拉索在自重静力状态下的轴力;le为拉索长度的换算值;l0为拉索的无应力长度;E为弹性模量;A为拉索截面面积;m为单位长度质量;n为模态阶数;Vn为拉索第n阶振动响应;ωn为拉索第n阶自振频率;ε为全桥结构阻尼比;a1为边界条件变动造成的参数激励项;a2为由垂度效应导致的非线性项系数;a3为由大幅振动位移导致的非线性项系数;a4为由于垂度效应使轴向力在横向产生的外激励;F为由拉索横向位移加速度导致的横向外激励;B为拉索上包含的j阶模态中其他阶模态的大幅振动对第n阶模态振动方程的影响。
对于第n阶模态,设模态函数为sin(nπx/l),可以推导得到上述各系数分别为
an=-lmgcos(θ)[cos(nπ)-1]nHπ,bn=n2π22l,cn=-n2π22l,dn=lmgcos(θ)[cos(nπ)-1]nHπ,en=l2,fn=-lcos(nπ)nπ
式中:g为重力加速度。
不同于文献[1],[10],[15]的推导,本文拉索端点位移激励作用下非线性振动方程式(2)中多了B这一项,B表示拉索上包含的j阶模态中其他阶模态的大幅振动对第n阶模态振动方程的影响。
由文献[1],[16]可知,平面拉索大幅振动动拉力h为
h=EAle(∫l0yxvxdx+12∫l0v2xdx)
(3)
式中:vx为对拉索局部坐标系下的x坐标求导。
将式(1)代入式(3),将拉索下垂曲线y近似为抛物线[18],可以得到拉索上同时存在j阶振动时拉索非线性振动的动拉力表达式为
h=EAle{2mglcos(θ)πHji=1[1-cos(iπ)]Vi2i+
π24lji=1(iVi)2}
(4)
1.2 索动力单元
基于拉索的直杆单元开发索动力单元,其单元刚度、质量矩阵与一般直杆单元相同[19]。当考虑索-梁相关振动时,有限元整体结构的振动方程为
M(t)+C(t)+Kδ(t)=F(t)+Fc(t)
(5)
式中:M为结构总体质量矩阵;K为总体刚度矩阵;C为总体阻尼矩阵;F(t)为结构上的总体外力向量;Fc(t)为在每一步计算中拉索非线性振动造成的等效总体节点外力向量;(t),(t),δ(t)分别为结构的加速度向量、速度向量和位移向量。
在本文编制的有限元计算程序中,为了使用索动力单元计算拉索振动,需要在有限元建模时通过设置,将某一根直杆单元标记为索动力单元,并设置拉索振动包含的模态阶数。
在动力特性计算中,程序会提取拉索静力构型下的轴力,根据式(2)各参数中拉索自振频率计算公式来计算拉索各阶自振频率。
在动力时程计算中,程序首先根据拉索静力构型下的轴力计算索动力单元中拉索振动方程式(1)的各个参数,然后在积分步循环中提取单元两端的位移响应,根据式(1)使用4阶Runge-Kutta数值积分方法计算拉索各阶模态振动响应,再根据式(4)叠加各个模态振动造成的拉索动拉力,按照式(5)计入有限元总体节点力中,从而计算得到拉索大幅度非线性振动与整体结构振动的互相作用。
在方程式(1)的建模过程中,拉索单元局部坐标系的解析方程建模坐标始终保持不变,而有限元模型单元坐标系中单元始末端可能不同,拉索的倾斜方向不同导致有限元单元坐标系的变化。在有限元计算中,提取节点在总体坐标系下的位移、速度、加速度后,程序自动按图2所示转换到理论方程建模坐标系,以保证端点位移激励的方向与理论方程式(1)的描述相统一,这样才能得到正确的拉索振动力,然后按照有限元法的规则得到拉索非线性振动力造成的单元节点力向量。
1.3 算法流程
斜拉桥全桥模型使用Newmark-β法动力时程积分[19]计算列车通过时动力荷载作用下的索-梁相关振动,本文程序基本计算流程见图3。
由图3可以看出,由于在有限元Newmark-β法动力时程计算中计入了各拉索大幅度非线性振动的动拉力导致的总体节点力,结构发生振动时拉索与整体有限元结构振动是相互影响的。
当列车过桥时,在每一步动力时程积分中提取的拉索端点位移反映了列车荷载对拉索的作用。拉索索力(对应端点位移变化)导致的振动状态变化在式(2)的参数激励项中可以体现出来。为了修正列车过桥时结构总体刚度矩阵的变化,在动力时程计算每个时间步中首先计算列车通过时拉索索力的增量,然后计算每个索动力单元的应力刚度矩阵,再叠加到自重静力构型状态的总体刚度矩阵上。
由于本文主要研究桥梁结构的振动响应,所以在计算中模拟列车通过桥梁时,列车模型使用了较为简单的平面双轴模型。列车与桥梁的耦合振动作用迭代计算方法与文献[20]相同,如图4所示。
2 算例分析
对于大跨度铁路斜拉桥,列车通过时的动力荷载是一个长期荷载,如果由于桥梁结构本身的特性,索-梁相关振动导致较大幅度的拉索振动,对桥梁结构安全是一个较大的威胁[21]。本文以具有代表性的天兴洲大桥南汊主桥为研究对象,考察其在列车通过时索-梁相关振动的特性。天兴洲大桥各设计参数可参考文献[17]。
2.1 拉索与全桥的动力特性
使用本文程序建立了天兴洲大桥简化的二维有限元模型(图5),主梁、桥塔使用平面梁单元模拟,单元参数按照实际桥梁的设计参数来换算。由于天兴洲大桥为三索面的斜拉桥,拉索处使用3根重合的索动力单元,各拉索编号如图5所示。全桥共202个节点,549个单元。
有限元模型的各约束设置为:各桥塔、桥墩底部完全约束,主梁两端约束Y0方向(竖向),主梁跨中约束X0方向(横向),塔梁连接处使用杆单元连接模拟支座。重力加速度g=9.8 m·s-2,拉索阻尼比设置为ε=0.001。文献[20]认为对于钢桥全桥结构阻尼比可设置为ε=0.02,为了得到偏于安全的结果,本文设置偏小的全桥结构阻尼比ε=0.01。
使用本文程序计算得到全桥在自重静力状态下的前6阶模态,如图6所示。
由图6可以看出,由于天兴洲大桥的主梁刚度较大,整体结构的低阶模态以主梁的振动为主。本文计算得到的全桥面内自振频率与文献[17]中的结果较为接近。
使用索动力单元可以一次计算得到所有拉索的前n阶自振频率。全桥为对称结构,全桥整体前10阶自振频率与第1~36号拉索的前2阶自振频率对比如图7所示,其中,J1表示全桥第1阶自振频率,其余类推。
由图7可以看出,对于天兴洲大桥,全桥振动的1阶自振频率接近跨中最长的32号拉索的1阶自振频率(0.430 1 Hz),全桥振动的2阶自振频率接近部分拉索的1阶自振频率,而全桥的3阶自振频率也接近部分拉索的2阶自振频率等。
由图7还可以看出,按照频率匹配的原则[1],从理论上可以判断,由于跨中最长的32号拉索1阶自振频率接近全桥的1阶自振频率,主梁发生振动时,索-梁相关振动导致拉索发生大幅共振的可能性是最大的。笔者认为列车通过时动力荷载作用下是否容易导致拉索产生较大幅度的振动需要通过计算才能明确判断。
2.2 外激励作用下斜拉桥索-梁相关振动特性
为了讨论拉索产生大幅度索-梁相关振动时全桥结构的振动特性,在模型跨中最长的32号拉索主梁上端点处施加动态力P=P0sin(ωt)(P0为力的幅值,ω为激励频率),见图8。
根据非线性振动理论可知[1-10],拉索发生2∶1的参数共振相对于1∶1的主共振需要更大的外激励频率。本文只考虑主共振的情况,探讨拉索发生大幅索-梁相关振动时桥梁结构的振动特性。
由拉索非线性振动理论可知,当端点位移激励频率接近拉索的1阶自振频率时,拉索容易在索-梁相关振动的作用下发生1∶1的主共振。设P0=-5×105 N,激励频率ω=0.430 Hz,接近跨中最长拉索的1阶自振频率。在动力时程积分中取时间步长为0.02 s,共计算12 500步。使用索动力单元,得到各拉索的1阶最大响应(最大振动响应绝对值),如图9所示。
从图9可以看出,32号拉索与33号拉索发生较大幅度的1阶振动,根据加载条件,可以判断拉索在索-梁相关振动的作用下发生1阶主共振。
由于斜拉桥为一个整体结构,所以外激励能量通过主梁与桥塔传递,导致全桥中与32号拉索自振频率接近的各拉索(1,33,64号拉索)都发生了较为明显的1阶振动。
得到32号拉索的1阶振动响应(图2中的局部坐标系下)以及拉索在主梁(节点39竖向振动)、桥塔上(节点177横向振动)端点振动响应的时程、频谱曲线如图10,11所示,其中,f为频率。
由图10,11可以看出,当外激励造成拉索端点位移激励频率接近拉索的1阶自振频率时,即使桥梁端点位移激励幅值较小,拉索也发生了较为明显的1阶主共振。拉索与主梁的振动体现了较为明显的非线性振动“拍振”现象[1]。
根据本文的研究,对于大跨度铁路斜拉桥,如果列车动力荷载造成拉索端点的位移激励频率接近拉索的自振频率,则索-梁相关振动必然会导致拉索发生较大幅度的共振。
2.3 列车通过时的全桥索-梁相关振动
与文献[20]类似,本文研究采用的列车模型为CRH2动车组平面双轴模型,共10节车厢,动力时程计算时空间步长取为0.15 m,时间步长按照车速与空间步长进行换算,轨道高低不平顺采用美国6级谱进行模拟,考虑拉索非线性振动包含前4阶模态。
以列车通过天兴洲大桥的最高设计时速250 km·h-1为上限,每隔10 km·h-1计算1次列车通过天兴洲大桥时的振动状态,共计算25次,从列车第1轮对进入桥梁开始计算,列车完全通过桥梁后第1轮对行驶至1 546 m时计算结束。
根据本文计算方法得到各拉索1,2阶振动最大响应与列车速度的关系,如图12所示,即列车过桥时各拉索1,2阶振动位移响应最大绝对值。
从图12(a)可知,边跨和跨中较长拉索在列车作用下有相对较为明显的响应,随着列车速度的增加,各拉索1阶最大响应的整体特性并无明显变化,只是随着列车速度的增加有了相对较小的增加。由图12(b)可以看出,拉索的2阶最大响应分布规律相对不明显,不同列车速度下拉索的2阶响应都很小。
为了考察不同速度下跨中最长拉索(32号拉索)在图2中拉索局部坐标系下的振动响应,以列车第1轮对位置为横坐标,绘制出在不同速度下一列列车通过天兴洲大桥时拉索的1阶振动响应,如图13所示。
由图13可以看出,跨中最长拉索在列车达到桥梁跨中(650 m处)时拉索有最大响应。当列车速度较小时,通过桥梁后拉索的周期振动不明显,当列车速度较大时,通过桥梁后拉索有较小的周期振动,幅值很小(约为0.01 m)。
以列车第1轮对位置为横坐标,绘制出不同速度下一列列车通过天兴洲大桥时32号拉索在主梁上的端部节点(靠近主梁1/2点的节点39)的竖向振动响应,如图14所示。
从图14可以看出,随着列车速度的增加,在设计速度250 km·h-1范围内,列车经过桥梁时主梁的振动响应特性是接近的。列车以较快速度通过桥梁时主梁有相对较为明显的周期振动,但幅值很小。
本文模拟的轨道不平顺中包含较高的频率成分,但靠近主梁1/2点的节点39响应曲线较为平滑,这说明由于天兴洲大桥主梁质量较大,轨道不平顺导致的列车振动力相对较小,对主梁作用不明显。3 计算结果分析与讨论
由以上分析可以看出,尽管跨中最长拉索较接近全桥的1阶自振频率,但对于天兴洲大桥,列车在设计时速范围内通过桥梁时各拉索并未观察到大幅度的索-梁相关振动现象。
根据本文第2节中的讨论以及文献[1],[10]中的研究,斜拉桥上的拉索如果在端点位移激励下发生较大幅度的振动,激励必须满足的条件为:①拉索端点具有相对较大激励幅值;②端点位移激励频率与拉索自振频率达到1∶1(主共振)或2∶1(参数共振)的匹配。笔者认为列车经过桥梁时,动力荷载未导致拉索发生较大幅度振动的原因在于列车通过时端点位移激励未达到上述条件。
从图14还可以看出,列车通过时拉索端部节点最大响应约为0.05 m,端点位移激励幅值已经达到激发共振的条件[1]。拉索虽然在列车通过时有较为明显的响应,但周期振动响应很小(图12)。因此,拉索未发生大幅振动的主要原因在于列车作用下拉索的端点位移激励频率相对拉索的自振频率较小。
列车作用下等效外激励频率与其通过速度有关,列车速度越快,等效外激励频率越高。提取列车以最高速度250 km·h-1通过桥梁时32号拉索主梁上端节点39的振动时程与频谱曲线,如图15所示。
从图15可以看出,列车作用下32号拉索在主梁上端节点的振动幅值相对较大,但造成的等效外激励频率较小,主梁上拉索端点振动频率仅为0.044 9 Hz,而拉索的1阶自振频率为0.430 1 Hz,频率的差别较为明显。因此,列车经过桥梁时拉索的振动响应更接近一个静力过程,如图16所示。
文献[22]针对列车引起桥梁共振的问题作了一系列的讨论,笔者研究发现文献[22]中的计算方法仅适用于简支梁的计算,并不适用于大跨度桥梁。究其主要原因是:从直观上来看,相对于小跨度的简支梁,列车的长度对于大跨度铁路斜拉桥全桥是较短的,大跨度斜拉桥主梁是较柔的,二者的整体宏观性质差别较为明显。
天兴洲大桥全桥1阶振动的振型以中跨1阶正对称振动为主(图6)。从直观上来看,对于对称的大跨度桥梁,列车在桥梁1阶振动的1个周期内通过桥梁跨中时可能造成桥梁共振而导致主梁大幅度的振动。
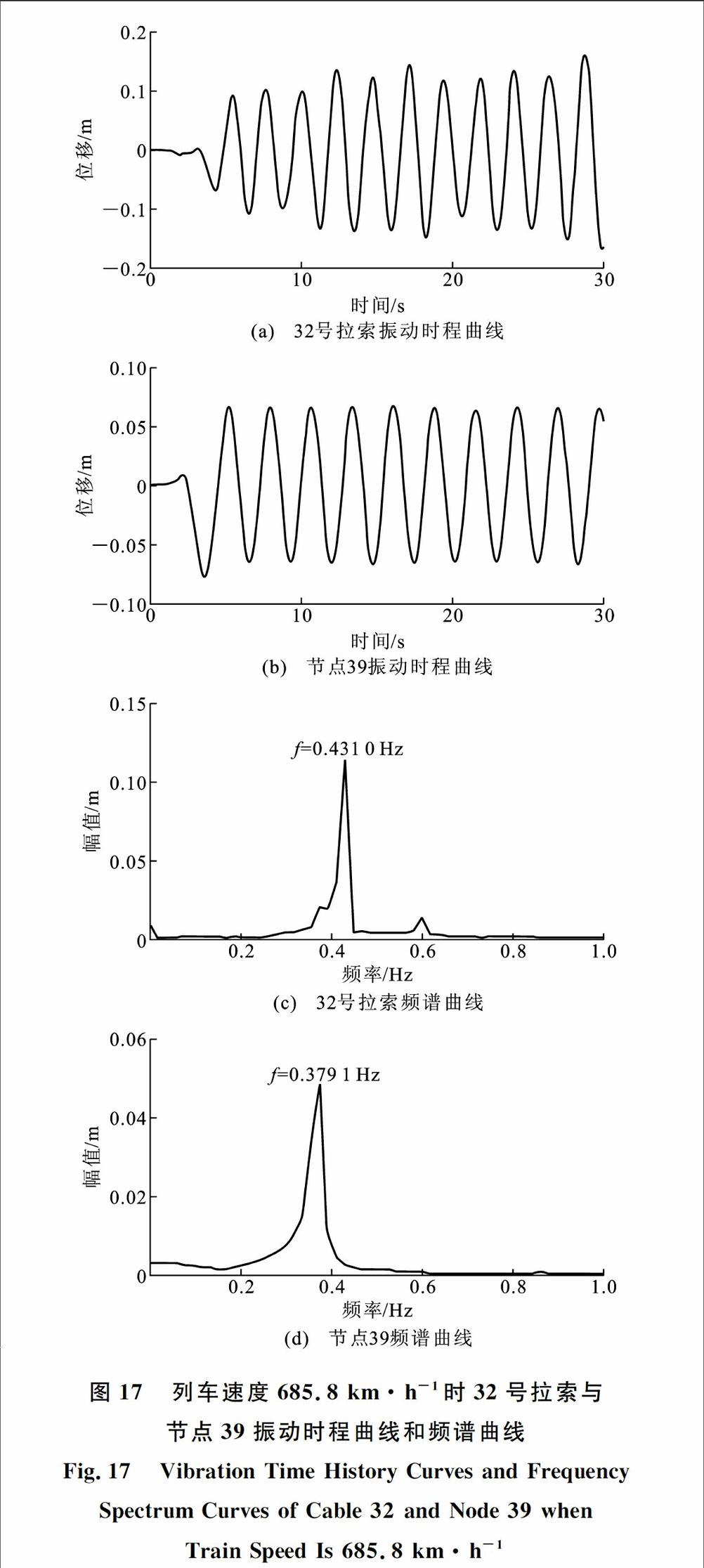
已知天兴洲大桥跨中长度为504 m,全桥的1阶自振频率为0.378 Hz,故列车引起桥梁共振的速度为685.8 km·h-1。设定一列列车经过桥梁的速度为686 km·h-1,其他设置不变,得到列车通过桥梁时32号拉索和拉索梁上端点(靠近主梁1/2点的节点39)的振动时程曲线和频谱曲线,见图17。
从图17可以看出,当列车以686 km·h-1的速度通过桥梁时,节点39振动频率成分以接近全桥1阶频率0.378 Hz为主。这说明列车在该速度下,列车的等效外激励频率接近了全桥的1阶自振频率,车桥耦合作用下全桥结构发生了明显的1阶共振。跨中最长拉索由于1阶自振频率较为接近梁上端节点振动频率,发生了相对较为明显的振动,幅值接近0.15 m。
对于天兴洲大桥,列车通过桥梁的最高设计速度为250 km·h-1,由以上分析可以判断,列车的设计速度远小于造成斜拉桥主梁发生较大幅值与较高频率振动的速度,在列车动力荷载的作用下斜拉桥拉索端点位移激励频率不会与拉索自振频率达到1∶1或2∶1的频率匹配,拉索不具备发生大幅度索-梁相关振动的条件。4 结 语
(1)计算结果表明,对于天兴洲大桥这样具有代表性的大跨度铁路斜拉桥,在设计速度范围内,列车过桥的动力荷载作用对桥梁造成的等效外激励频率较低,拉索端点振动频率不会达到拉索发生1∶1主共振或2∶1参数共振的条件。索-梁相关振动不会导致拉索发生大幅度振动。拉索的响应接近一个静力过程(列车速度较大时仅发生很小幅度的周期振动),本文认为该拉索是安全的。
(2)由于大跨度铁路斜拉桥主梁质量通常很大,轨道不平顺导致的列车振动力相对很小,尽管本文模拟的轨道不平顺包含一些高频率的成分,但不会导致桥梁发生共振,桥梁的动力响应主要来源于列车过桥时在自重作用下的冲击力作用。
(3)根据计算结果,笔者建议在一般斜拉桥的设计中应当使全桥各拉索中最低的1阶自振频率(通常是最长拉索)超过全桥整体结构的2阶自振频率,这样是更为安全的。对于大跨度斜拉桥,由于主梁质量较大,全桥整体结构自振频率较小,这个条件通常是自然满足的。对于某些特殊的斜拉桥,如跨度小、主梁质量小、索力小、拉索自振频率也相对较小的人行斜拉桥,应当按照上述原则充分考虑避免拉索局部频率与整体结构频率的匹配。
参考文献:
References:
[1] 陈水生.大跨度斜拉桥拉索的振动及被动、半主动控制[D].杭州:浙江大学,2002.
CHEN Shui-sheng.Vibration,Passive and Semi-active Control of Cables for Large-span Cable-stayed Bridges[D].Hangzhou:Zhejiang University,2002.
[2]李永乐,赵 凯,吴梦雪,等.斜独塔混合梁斜拉桥风-汽车-桥梁系统耦合振动研究[J].中国公路学报,2012,25(1):47-54.
LI Yong-le,ZHAO Kai,WU Meng-xue,et al.Study of Coupling Vibration of Wind-vehicle-bridge System for Inclined Single Pylon Cable-stayed Bridge with Hybrid Girder[J].China Journal of Highway and Transport,2012,25(1):47-54.
[3]颜东煌,陈常松,董道福,等.大跨度钢主梁斜拉桥的自适应无应力构形控制[J].中国公路学报,2012,25(1):55-58,82.
YAN Dong-huang,CHEN Chang-song,DONG Dao-fu,et al.Control of Self-adaptive Zero-stress Configuration for Long-span Cable-stayed Bridge with Steel Main Girders[J].China Journal of Highway and Transport,2012,25(1):55-58,82.
[4]李 岩,吕大刚,盛洪飞.考虑随机车载-风载联合作用的斜拉桥拉索疲劳可靠性分析[J].中国公路学报,2012,25(2):60-66.
LI Yan,LU Da-gang,SHENG Hong-fei.Fatigue Reliability Analysis on Cable of Cable-stayed Bridge Under Random Vehicle Load and Wind Load[J].China Journal of Highway and Transport,2012,25(2):60-66.
[5]熊 文,肖汝诚,CAI C S,等.基于力学与造价的CFRP-钢组合拉索斜拉桥设计理论[J].中国公路学报,2012,25(4):97-106.
XIONG Wen,XIAO Ru-cheng,CAI C S,et al.Design of Cable-stayed Bridges with CFRP-steel Composite Stay Cables Based on Mechanical and Economical Behaviors[J].China Journal of Highway and Transport,2012,25(4):97-106.
[6]方 志,张国刚,唐盛华,等.混凝土斜拉桥动力有限元建模与模型修正[J].中国公路学报,2013,26(3):77-85.
FANG Zhi,ZHANG Guo-gang,TANG Sheng-hua,et al.Finite Element Modeling and Model Updating of Concrete Cable-stayed Bridge[J].China Journal of Highway and Transport,2013,26(3):77-85.
[7]张宏杰,朱乐东,胡晓红.超千米级斜拉桥抗风稳定性风洞试验[J].中国公路学报,2014,27(4):62-68.
ZHANG Hong-jie,ZHU Le-dong,HU Xiao-hong.Wind Tunnel Test on Wind-resistant Stability of Super-kilometer Cable Stayed Bridge[J].China Journal of Highway and Transport,2014,27(4):62-68.
[8]吴文朋,李立峰,邵旭东,等.基于性能的中等跨径混凝土斜拉桥抗震风险分析[J].中国公路学报,2015,28(3):52-59,116.
WU Wen-peng,LI Li-feng,SHAO Xu-dong,et al.Performance-based Seismic Risk Analysis for Medium-span Concrete Cable-stayed Bridges[J].China Journal of Highway and Transport,2015,28(3):52-59,116.
[9]董国朝,陈政清,罗建辉,等.安装亮化灯具导致的斜拉桥拉索风致驰振流固耦合分析[J].中国公路学报,2012,25(1):67-75.
DONG Guo-chao,CHEN Zheng-qing,LUO Jian-hui,et al.Fluid-structure Interaction Analysis of Wind-induced Galloping of Cables with Lamps of Cable-stayed Bridge[J].China Journal of Highway and Transport,2012,25(1):67-75.
[10]周海兵.索-梁组合结构非线性动力学实验研究[D].长沙:湖南大学,2007.
ZHOU Hai-bing.The Experimental Investigation on Nonlinear Dynamics of Cable-beam Structure[D].Changsha:Hunan University,2007.
[11]GATTULLI V,LEPIDI M.Localization and Veering in the Dynamics of Cable-stayed Bridges[J].Computers & Structures,2007,85(21):1661-1678.
[12]LORENZO R,MACDONALD J H G.Experimental Validation of a Simplified Cable-stayed Bridge Model Exhibiting Autoparametric Resonance[C]//AIM.Proceedings of 5th International Symposium on Cable Dynamics.Santa Margherita:AIM,2003:165-172.
[13]CAETANO E,CUNHA A,GATTULLI V,et al.Cable-deck Dynamic Interactions at the International Guadiana Bridge:On-site Measurements and Finite Element Modeling[J].Structural Control and Health Monitoring,2008,15(3):237-264.
[14] ZHANG H,XIE X.Dynamic Responses of Cable-stayed Bridges to Vehicular Loading Including the Effects of the Local Vibration of Cables[J].Journal of Zhejiang University:Science A,2011,12(8):593-604.
[15]CAETANO E.Cable Vibrations in Cable-stayed Bridges[M].Zurich:IABSE,2007.
[16]王 涛,沈锐利,李 洪.斜拉桥索-梁相关振动概念及其研究方法初探[J].振动与冲击,2013,32(20):29-34.
WANG Tao,SHEN Rui-li,LI Hong.Primary Exploration for Concept and Studying Method of Cable-beam Vibration in a Cable-stayed Bridge[J].Journal of Vibration and Shock,2013,32(20):29-34.
[17]秦顺全.武汉天兴洲公铁两用长江大桥关键技术研究[M].北京:人民交通出版社,2009.
QIN Shun-quan.Key Technologics Study of Tianxingzhou Rail-cum-road Yangtze River Bridge in Wuhan[M].Beijing:China Communications Press,2009.
[18]王 涛,沈锐利,郭 健.考虑抗弯刚度的缆索线形研究[J].建筑科学与工程学报,2010,27(3):35-40.
WANG Tao,SHEN Rui-li,GUO Jian.Research on Suspended Curve-shape of Cables Considering Flexural Rigidity[J].Journal of Architecture and Civil Engineering,2010,27(3):35-40.
[19]徐荣桥.结构分析的有限元法与MATLAB程序设计[M].北京:人民交通出版社,2006.
XU Rong-qiao.Finite Element Method in Structural Analysis and MATLAB Programming[M].Beijing:China Communications Press,2006.
[20]翟婉明,夏 禾.列车-轨道-桥梁动力相互作用理论与工程应用[M].北京:科学出版社,2011.
ZHAI Wan-ming,XIA He.Train-track-bridge Dynamic Interaction:Theory and Engineering Application[M].Beijing:Science Press,2011.
[21]李永乐,王云飞,周 昱,等.辅助墩对大跨度铁路悬索桥抗震性能及列车走行性的影响[J].建筑科学与工程学报,2014,31(3):32-37.
LI Yong-le,WANG Yun-fei,ZHOU Yu,et al.Influence of Auxiliary Piers on Seismic Behavior and Train Runability for Long-span Railway Suspension Bridge[J].Journal of Architecture and Civil Engineering.2014,31(3):32-37.
[22]沈锐利.高速铁路线上简支梁桥车桥共振问题初探[J].西南交通大学学报,1995,30(3):275-282.
SHEN Rui-li.Preliminary Research of Bridge-vehicle Resonance on Simple-supported Beam Bridges on High Speed Railways[J].Journal of Southwest Jiaotong University,1995,30(3):275-282.
