基于供应链网络管理的企业竞争与合作互补模型与算法＊

朱浩玮，张 飞，张西锦，任庆军，孙洪春

（临沂大学理学院，山东 临沂276005）

引言

从世界范围来看，企业经营面临的外部环境发生了巨大变化，越来越体现出“多样化、个性化”特征．企业之间的竞争，已经由过去的相对简单、静态、缓和转变到如今的较为复杂、动态和激烈．随着全球经济一体化和区域经济集聚化趋势的不断加强，企业逐渐认识到：仅凭某个企业的资源和能力，走内部挖潜道路，已经很难在激烈的市场竞争中长久地立于不败之地．“在全球性的市场中‘完全损人利己的时代已经结束’，为了竞争必须合作．”（乔尔·布利克，1998），使企业双赢乃至多赢成为可能．

供应链网络管理，主要用于研究供应链上企业的布局、竞争和合作等问题．已成为现代物流研究的一个热门课题，引起了国内外许多学者浓厚的研究兴趣（参看综述文献［1，2］）．Nagur ney等［3］建立了三层供应链网络均衡变分不等式模型．Dong等［4］研究了拥有随机需求的有限维变分不等式为供应链网络模型．Cheng等［5］基于Wardrop均衡原理建立了多产品的供需网络均很模型．徐兵等［6］研究了产品随机选择下的多商品流供应链网络均衡模型．滕春贤等［7，8］研究了随机需求下供应链网络均衡问题以及供应链网络均衡模型．Choi等［9］研究了价格竞争环境下的产品定位问题，并构建了具有优化结构的均衡模型．

供应链网络管理具有典型的层次性，供应链网络中上下层之间的竞争和合作问题是供应链管理中研究的重要问题．供应链网络中的上下层之间常常既具有竞争也有合作的博弈关系．因为处于上层的决策者通常处于主导地位，而处于下层的决策者在上层给出决策参数后，分别选择自己的最佳决策，下层决策者又是追求个体利益最大化的独立经济主体，处于非合作博弈状态，最终达到某种均衡态．这样在供应链网络系统中，就同时具有了上下层之间的竞争合作博弈关系和下层成员之间的非合作博弈关系，如何刻画供应链网络中的这种关系，进而揭示出供应链网络中处于上下层的成员间的竞争和合作关系就显得尤为重要．

本文利用均衡理论和二层规划理论，对具有一个制造商和多个零售商的供应链网络系统进行了研究，分析了同层零售商之间的竞争行为以及制造商和零售商之间的竞争合作关系，构建了二层供应链网络的互补模型，并提出了求解该模型的一个新算法，在较宽松的条件下，证明了所给算法的全局收敛性和二次收敛率．本文的研究对分析供应链成员间的竞争和合作等问题具重要的理论和实际意义．

1 互补模型的构建

在供应链网络结构中，假设有一个制造商和多个零售商，制造商处于占主导的地位，零售商属于跟随者，顾客在零售商处购买的产品数量是随机的．

1．1 零售商的最优性条件

以单个销售季为研究对象，令Dj表示零售商j的随机需求量，是随机变量，Fj为随机需求的分布函数，fi为相应的密度函数，且μj表示数学期望需求量，即μj＝E（Dj）．假定零售商j处的零售价格为pj，用表示零售商j同制造商交易时所发生的交易成本．令Sj表示零售商的期望销售量，用qj表示制造商送给零售商j的产品量，则

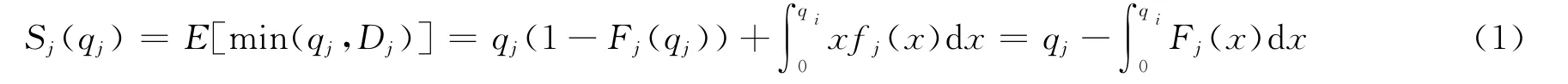
令Ij表示零售商j没有销售完的期望剩余库存，假定这些剩余的产品在销售季末将以单位价格vj处理，则

令Lj表示零售商j处供不应求时的缺货量，则：

如果发生缺货，则顾客会空手而归以至于零售商和整个行业遭受一定商誉损失．用grj表示零售商处的缺货对零售商j造成的商誉损失成本．

基于以上分析，为实现零售商的利润最大，其利润等于其收益减去相应的成本，用πj表示零售商j的利润，则有

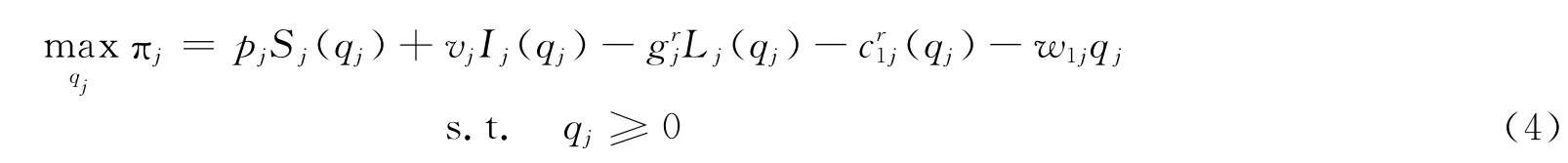
由（2）、（3）、（4），得

其中制造商给零售商j的批发价格记为w1j，j＝1，···，n．

假设每一个零售商将在他的竞争对手达到最优状态下做出自己的定购量．由假设，零售商的成本函数为连续可微的凸函数，则所有零售商达到均衡就等价为如下问题，即求解q∈，满足

1．2 制造商的最优性条件

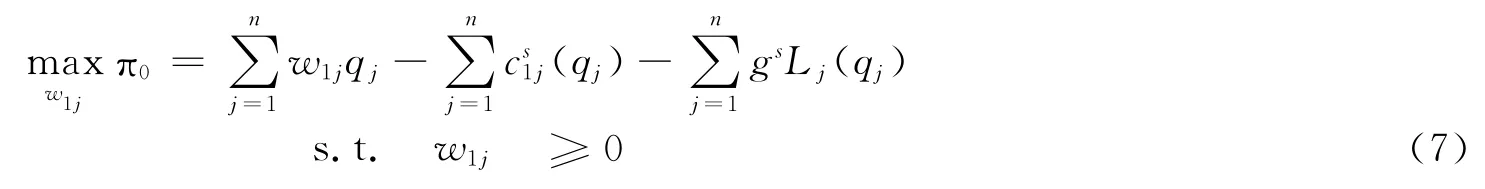
由（3），则

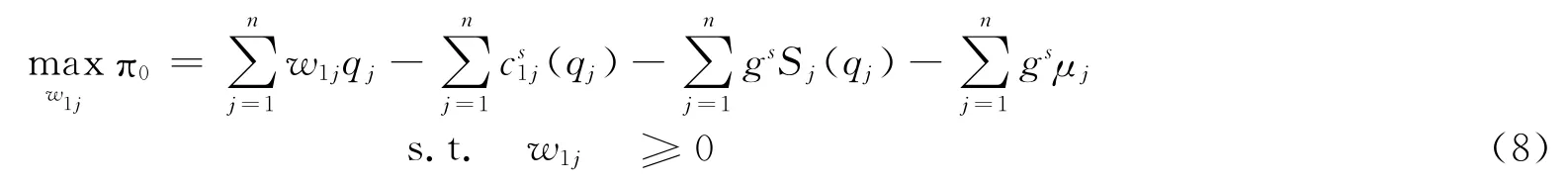
1．3 基于供应链网络的企业竞争与合作模型

对整个供应链网络系统而言，制造商处于供应链网络的上层占主导地位，首先给出批发价格．处于供应链网络下层的零售商再根据上层制造商的批发价格，确定其最优的订购量，处于下层的各个零售商属于非合作博弈，继而达到均衡态．

上层为制造商的利润最大化问题：

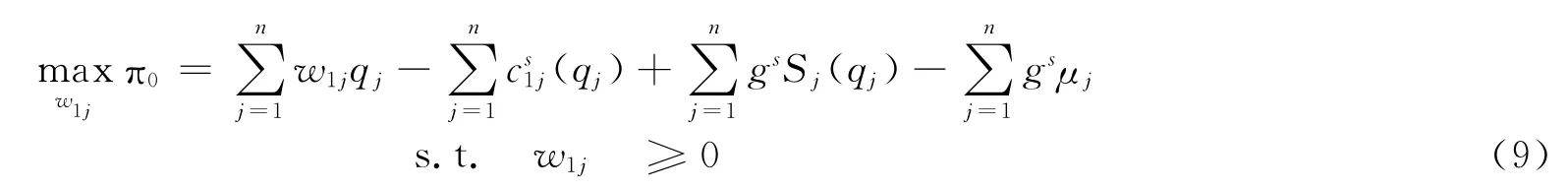
下层所有零售商达到均衡状态等价为如下问题，即，对给定的w1∈Rn＋使得

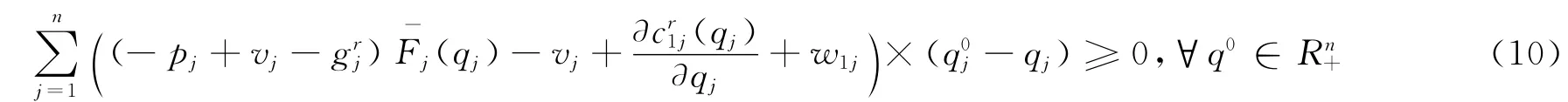
因此，基于供应链网络的企业竞争与合作模型：

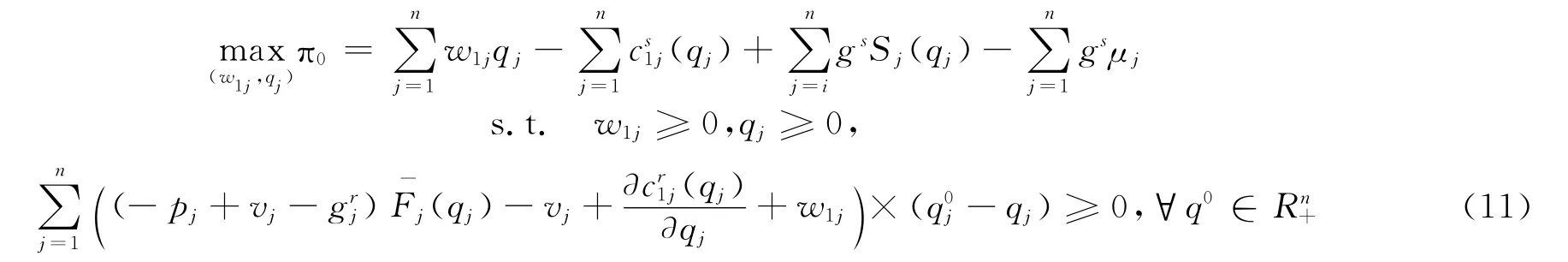
显然，（10）等价于下面的互补问题，即求解q∈Rn＋使得

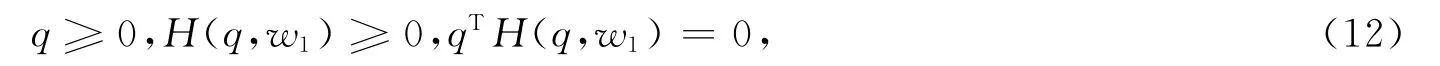
其中q＝（q1，q2，···，qn）T，w1＝（w11，w12，···，w1n）T，

下面，为给出（12）的一个等价转化，首先给出下面的Fischer函数［10］，其定义为φ：R2→R1且φ（a，b）＝且有下面性质：

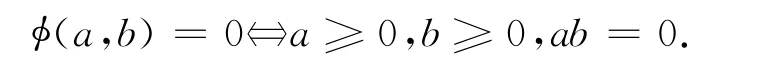
同时，Tseng［11］也给出了下面的结论

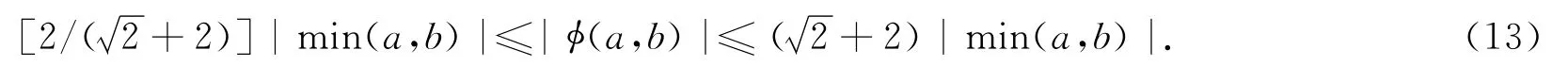
因此，对任意向量a，b∈Rn，定义一个向量函数

基于以上分析，（12）等价于等式Φ（q，H（q，w1）＝0．（11）等价的转化为：

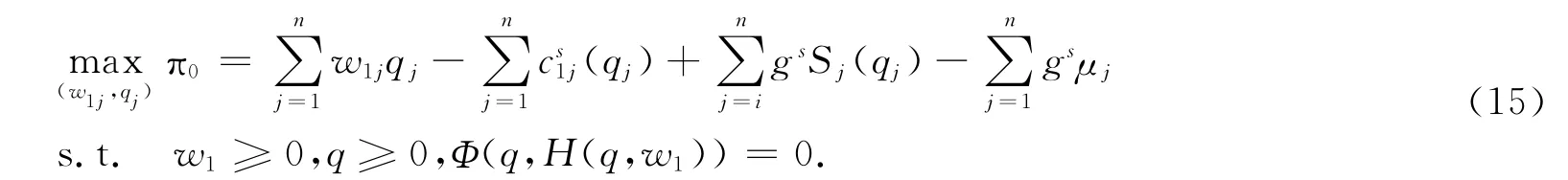
为进一步等价转化（15）为一互补问题，对给定的向量函数Θ给出B－次微分的定义和计算方法．

定义2．1［12］设Θ：Rn→Rm为Rn上局部Lipschit z连续函数，则其B－次微分定义为∂BΘ（x）＝，对于所有的k，Θ（x）在xk处可微｝．

Clar ke（［12］）广义Jocobian微分定义为B－次微分的凸包，即∂Θ（x）＝co∂BΘ（x）．借助B－次微分的定义给出半光滑和强半光滑的定义．

定义2．2［12］局部Lipschit连续向量函数Θ：Rn→Rm在x∈Rn半光滑，若极限对任意h∈Rn存在．

易知，若函数Θ在x点半光滑，则Θ在x点沿任意方向h∈Rn的方向导数都存在．下面是关于半光滑函数的性质［13］．

定理2．1［13］设Θ：Rn→Rm为局部Lipschit Q连续函数且半光滑，则如下结论成立：

a）对任意V∈∂Θ（x＋h），h→0，Vh－Θ′（x；h）＝O（‖h‖）；

b）对任意h→0，Θ（x＋h）－Θ（x）－Θ′（x；h）＝O（‖h‖）．

半光滑函数介于Lipschitz函数和连续可微函数之间，连续可微函数与凸函数都是半光滑函数，比半光滑稍强的概念是强半光滑．

定义2．3［13］函数Θ：Rn→Rm称为在x点强半光滑，若Θ在x半光滑，且对任意V∈∂Θ（x＋h），h→0有Θ（x＋h）－Θ（x）－Vh＝O（‖h‖2）．

下面讨论向量值函数φ（x，y）＝（φ（x1，y1），φ（x2，y2），．．．，φ（xn，yn））的微分性质．特别地，给出φ（x，y）关于（x，y）的Clar ke广义Jacobian矩阵的估计．为了方便，用∂φ（x，y）表示φ（x，y）关于（x，y）∈R2n的Clar ke广义Jacobian矩阵，类似于文献［14］中命题3．1的讨论，有如下结论．

引理2．1［14］对任意（x，y）∈R2n，∂Ψ（x，y）⊆（Da，Db），其中

ai＝ξi－1，bi＝ηi－1，对任意（ξi，ηi）∈R2使得‖（ξi，ηi）‖≤1，若＋＝0基于以上分析，（15）的KKT条件为：存在λ1∈R2n，λ2∈R2n使得

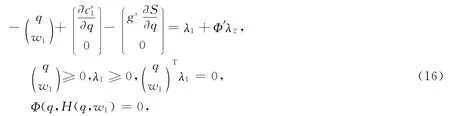
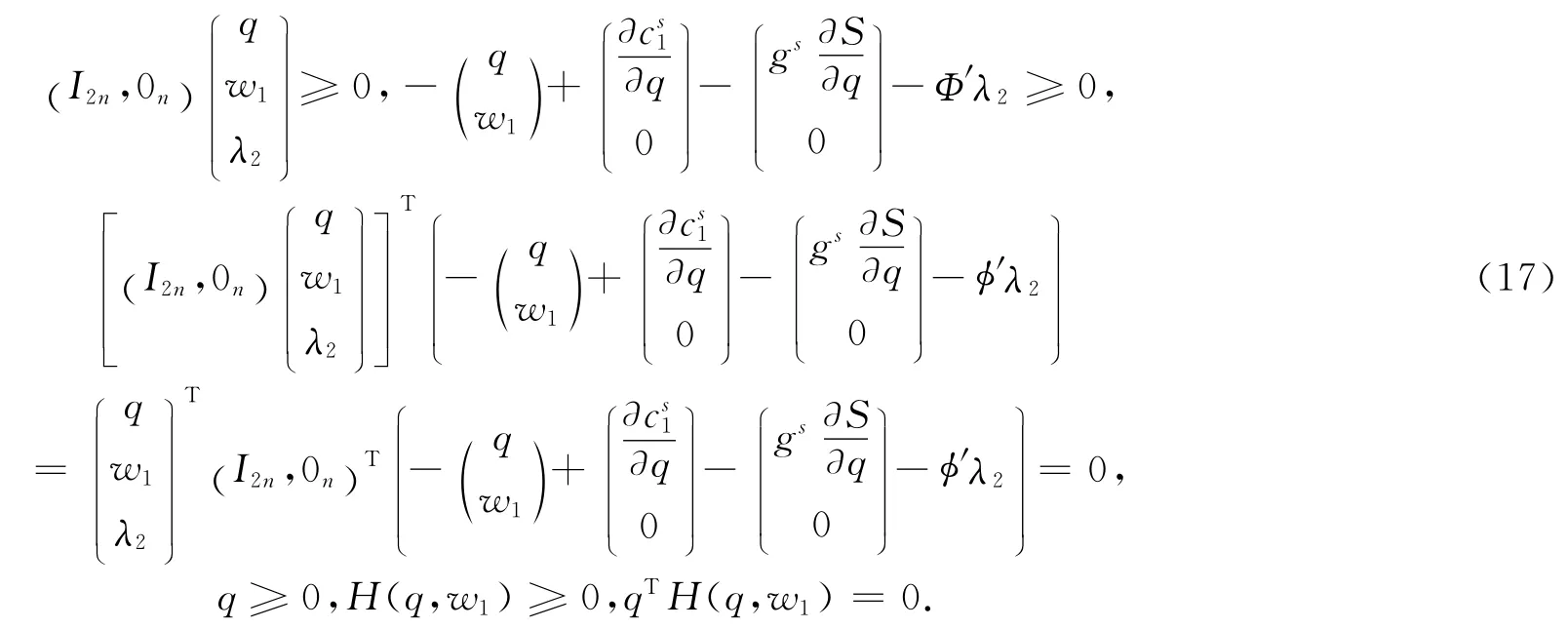
令

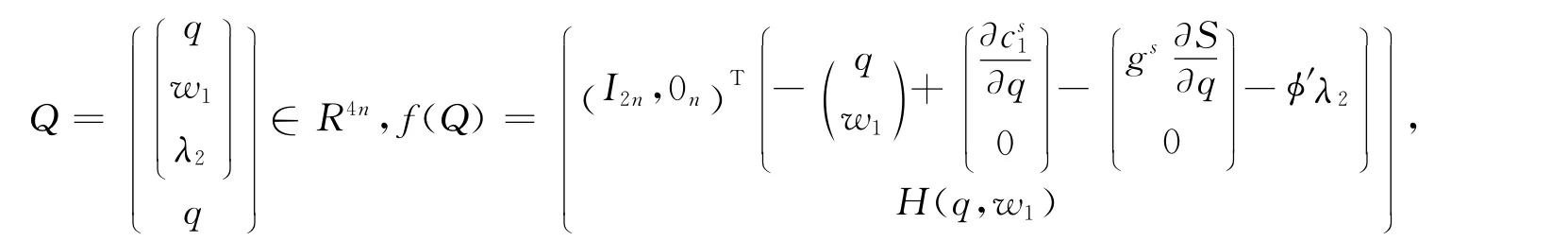
则（17）等价于下面的互补问题，求一向量Q∈R4n使得

当上层的制造商给出批发价格以后，下层的零售商以上层制造商的批发价格为参数，进行非合作博弈，继而达到均衡状态，下层的零售商再把均衡解（订购量）反馈给上层的制造商，制造商最后选择自己的最优方案．

2 模型的算法及收敛性

对于实际问题，可用多项式进行曲线拟合，因此，模型（18）中的映射函数可假设为多项式函数，且要求在一个有界区域内求解．因此，在f（Q）是一个多项式函数和Q有界的假设下，给出求解（18）的一个新算法，并证明算法的全局收敛性和二次收敛率．为此首先建立（18）的误差界．

定理3．1 假设f（Q）是一个多项式函数，且次数为正整数s≥1，对给定的正常数ρ，存在一个常数η1＞0使得dist∀Q，‖Q‖≤ρ，其中r（Q）＝‖min｛Q，f（Q）｝‖，dist（Q，X＊）表示任给点Q到解集合X＊的距离．

证明 假设命题不成立，则存在序列｛Qk｝，对于任意的正整数k，皆有

即

其中‖Qk‖≤ρ．因序列｛Qk｝有界，且r（Q）是连续的，结合（19），有r（Qk）→0，k→∞，同时序列｛Qk｝存在收敛的子序列｛Qki｝，不妨设其中因f（Q）是一次数为S的多项式函数，因此，有

式中，β是一个正常数．另外，由（19），有：

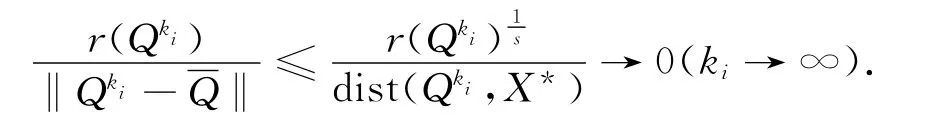
这与（20）矛盾，所以命题结论成立．

基于（14），系统（18）等价转化为下面等式

Φ（Q，f（Q））＝（φ（Q1，f1（Q）），φ（Q2，f2（Q）），…，φ（Qn，fn（Q））T＝0．

显然，利用（13）和定理3．1，易有下面结论成立．

定理3．2 假设f（Q）是一个多项式函数，且次数为正整数s≥1，对给定的正常数ρ，存在一个常数η2＞0使得dist（Q，X＊）≤η2‖Φ（Q）‖，｜Q｜≤ρ．

下面，给出函数ρ：R＋→R，

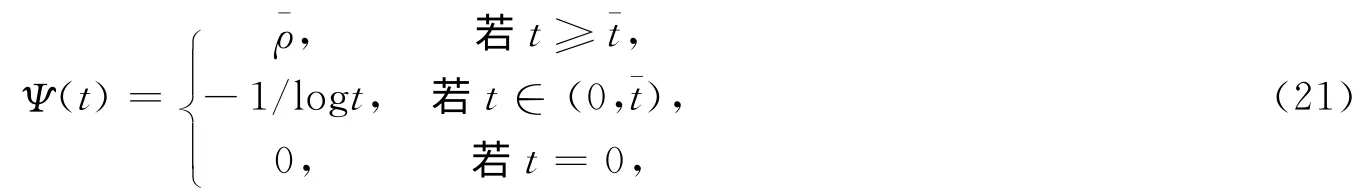
定理3．3 假设f（Q）是一个多项式函数，且次数为正整数s≥1，对给定的正常数ρ，存在一个常数c1＞0，使得dist（Q，X＊）≤c1Ψ（‖Φ（Q）‖），‖Q‖≤ρ．

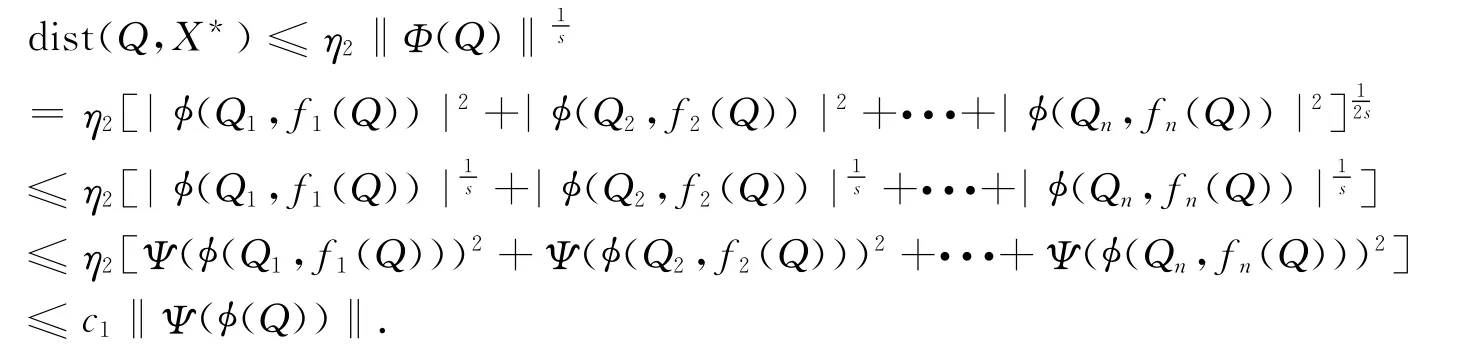
其中Ψ（φ（Q））＝（Ψ（｜φ（Q1，f1（Q））｜），Ψ（φ（Q2，f2（Q））），···，Ψ（φ（Qn，fn（Q）））2）T，c1＝η2．

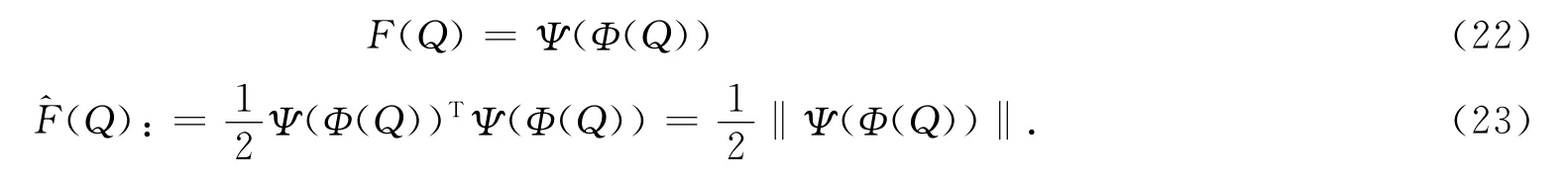
基于定义2．3和（22）和（23），利用定义2．3，有如下结论．

定理3．4［14，15］对于（22）和（23）定义的向量函数F和实值函数，如下结论成立

下面，给出求解问题（18）的一个收敛算法，并且利用建立的误差界结果，在不要求存在非退化条件下，证明所给光滑算法的二次收敛性．

算法3．1

步1：选取初始点Q0，参数σ，β，γ∈（0，1）和ε≥0，令k＝0．

步3：任选Hk∈∂F（Qk），取dk为以下线性方程组的解

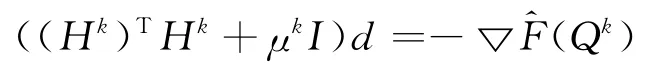
其中μk＝σ‖F（Qk）‖2．

步4：令mk为满足如下条件的最小非负整数

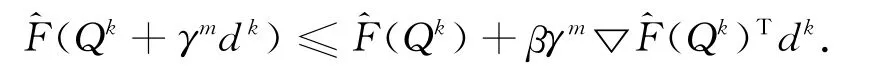
令Qk＋1：＝Qk＋γmkdk，k：＝k＋1，转步2．

容易证明dk为F（Q）在Q的下降方向，故算法3．1是有定义的．显然，若▽F（Qk）＝0，则Qk为稳定点，从而在适当的条件下，Qk为（18）的解．在下面的算法收敛性分析中，假设算法3．1产生一个无穷点列，即Qk不是稳定点．

定理3．5 设｛Qk｝为算法3．1产生无穷点列，则｛Qk｝的任一聚点都是下面问题的稳定点．

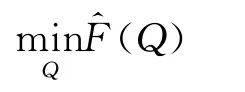
证明：设Q＊为｛Qk｝的任一聚点，则存在无穷子列K⊆｛1，2，…｝使得｛Qk｝K→Q＊．由次微分的上半连续性可知，｛Hk｝k∈K有界．不妨设相应的子列

｛（Hk）｝K→H＊，｛μk｝K→μ＊，

从而有｛（Hk）THk＋μkI｝K→（H＊）TH＊＋μ＊I．

定理3．6 假设算法3．1产生的序列为｛Qk｝，当Qk充分的靠近F（Q）＝0的解Q＊，则有｛dist（Qk，X＊）｝二次收敛到0，即序列｛Qk｝二次收敛到∈X＊．

注：定理3．1表明在不要求存在非退化条件下，所给的光滑算法具有二次收敛性，这是一个新的结果．

［1］Poirier C C．Supply Chain Opti mization：Building a Total Business Net wor k［M］．Berrett－Kochler Publishers，San Francisco，Calif ornia，1996．

［2］Poirier C C．Advanced Supply Chain Management：How to Build a Sustained Co mpetitive Advantage［M］．Berrett－Kochler Publishers，San Francisco，California，1999．

［3］Nagur ney A，Dong J，Zhang D．A Supply chain net wor k equilibriu m model［J］．Transportation Research E，2002，38：281－303．

［4］Dong J，Zhang D．Nagur ney A，A supply chain net wor k equilibriu m model with rando m demands［J］．European Jour nal of Operational Research，2004，156：194－212．

［5］Cheng T C E，Wu Y N．A multiproduct，multicriterion supply chain－demand net work equilibrium model［J］．Operations Research，2006，54，（3）：544－554．

［6］徐兵，朱道立．产品随机选择下多商品流供应链网络均衡模型研究［J］．系统工程理论与实践，2007，3：82－90．

［7］滕春贤，姚峰敏，胡宪武．具有随机需求的多商品流供应链网络均衡模型的研究［J］．系统工程理论与实践，2007，10：77－83．

［8］滕春贤，胡引霞，周艳山．供应链网络均衡模型应对突发事件［J］．系统工程理论与实践，2009，3：16－20．

［9］Choi C S，Desar bo W S，Har ker P T．Pr oduct positioning under price co mpetition．Management Science，1990，36（2）：175－199．

［10］Fischer A．A special Newton－type opti mization met hod［J］．Opti m．，1992，24：269－284．

［11］Tseng P．Growth behavior of a class of merit f unction f or the nonlinear co mplementarity problem［J］．J．Opti m．Theor y Appl．，1996，89：17－37．

［12］Clar ke F H．Opti mi Qation and Nons mooth Analysis［M］．John Wiley and Sons，New Yor k，NY，1983．

［13］Qi L．，Sun J．．A nons mooth version of Newton’s method［J］．Math．Programming，1993，58：353－367．

［14］Facchinei F，and Soares J．A new merit f unction f or nonliner co mplementarity problems and a related algorith m［J］．SIAM J．Opti m．，1997，7：225–247．

［15］Facchinei F，Kanzowb C．A nons mooth inexact Newton method f or the solution of large－scale nonlinear co mplementarity problems．Mat h．Programming，1997，76：493－512．

［16］Facchinei F．Minimization of SC1f unctions and Maratos effect．Operations Research Letters，1995，17：131－137．

［17］Yamashita N，Fukushi ma M．On the rate of conver gence of the Levenber g－Marquardt met hod［J］．Co mputing，2001，15：237－249．