水下卧式采油树油管挂出油口角度的优化设计

秦 蕊，李清平，罗晓兰，段梦兰

(1. 中海油研究总院，北京 100028；2. 中国石油大学(北京)海洋油气研究中心，北京 102249)

水下卧式采油树油管挂出油口角度的优化设计

秦 蕊1，李清平1，罗晓兰2，段梦兰2

(1. 中海油研究总院，北京 100028；2. 中国石油大学(北京)海洋油气研究中心，北京 102249)

针对减少流动损失这一工程问题，通过分析油管悬挂器的结构特点，综合考虑其在水下卧式采油树中的位置和功能，基于阻力系数方法提出了油管悬挂器出油口角度的优化设计方法。同时，采用FLUENT软件对不同出油口角度下的油管悬挂器内部流体流动进行数值模拟，为理论设计方法提供证明和依据。最终得到的理论计算结果和数值模拟结果均表明：出油口角度在11°～12°之间时流动损失最小。

海底管道；水下卧式采油树；油管挂；出油口角度；优化设计

0 引 言

随着海上油气田开发的推进，深水油气田的开发逐步成为人们关注的焦点。水下生产系统作为适于深水油气田开发的主要模式之一，在巴西、挪威等地的海域均有广泛应用[1-2]。在水下生产系统中，采油和外输的关键设备是水下采油树，因此，世界各国的学者、专家在技术理论、数值模拟及结构设计方面均对水下采油树进行了深入的探索和研究。但国内在这方面的研究刚刚起步。

在水下卧式采油树正常生产期间，其内部流体的能量是否足以满足整个流程的动力需求，这是水下卧式采油树面临的最主要工程问题之一。水下卧式采油树的结构复杂，包括油管悬挂器、主阀、翼阀、采油树本体和出油管等部件，其中油管悬挂器直接决定着水下采油树的整体性能及外输能力。本文给出了油管悬挂器出油口角度的优化设计，可以减少水下卧式采油树内流体的流动阻力，从而使得采油树内部流体的能量满足动力需求。

1 水下卧式采油树油管悬挂器的结构

油管悬挂器位于水下卧式采油树内，如图1所示[3]。油管悬挂器与位于水平通道上的生产主阀和生产翼阀以及采油树本体和出油管等部件组成了水下卧式采油树的过流部件，是井下流体向外输送的唯一通道。

油管悬挂器的结构可分为外部结构和内部结构两部分，如图2所示[4]。其中外部结构按照功能、作用的不同可分为锁定机构、密封机构和定向机构；内部结构则包括内部通路(包括数量和尺寸两个影响因素)和内部型面两个方面。

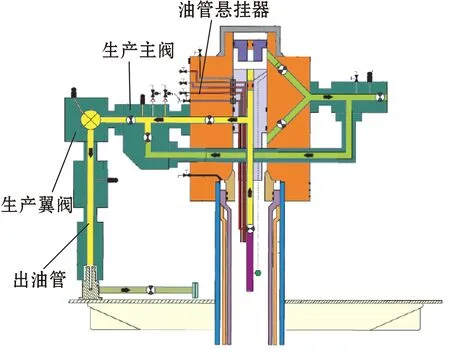
图1 油管悬挂器的位置Fig.1 Position of the tubing hanger

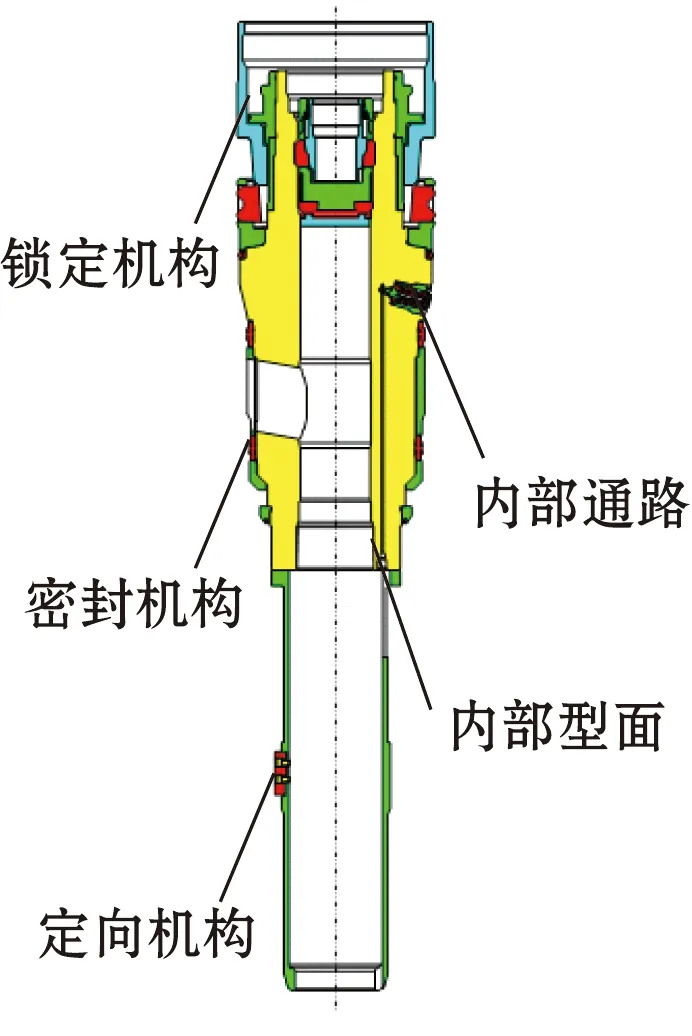
图2 油管悬挂器的结构Fig.2 Structure of the tubing hanger

2 油管挂出油口角度的优化设计

水下卧式采油树油管挂与采油树本体之间组成一个弯曲的管路，使得生产流体的流向发生改变，从而产生离心力。离心力的出现使得弯管内外壁处流体流速发生相对变化，即在外壁处流速减小，而在内壁处流速相应增大，从而形成涡流副，造成压力损失，影响流体的流动。另外，内壁处流速增大还会使流体对油管挂出油口处的冲击变大。那么，在何种转弯角度下可以使得压力损失最小，并减小冲击呢？这便是本文所研究的油管悬挂器出油口角度优化的目的与判断标准。

压力损失的多少与弯管中阻力系数的大小有关，因此，采用阻力系数法对不同出油口角度的阻力系数进行计算，从而得到流动损失最小的出油口角度。

油管悬挂器内部通路的简化模型如图3所示，可近似看为带盲管的锐角边粗糙壁弯管与不带盲管的锐角边粗糙壁弯管的合成，如图4和图5所示。

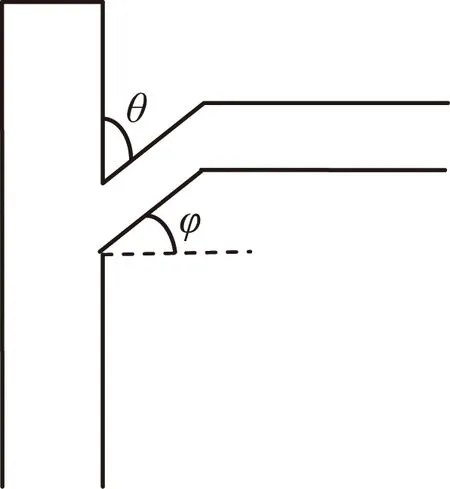
图3 油管悬挂器内部通路简图Fig.3 Internal pathway of the tubing hanger

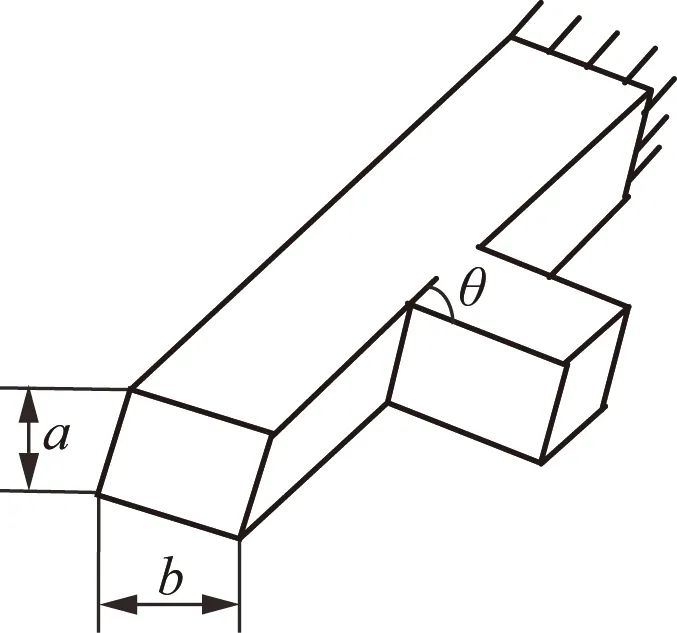
图4 带盲管的锐角边弯管Fig.4 Acute angle bending pipe with blind tube

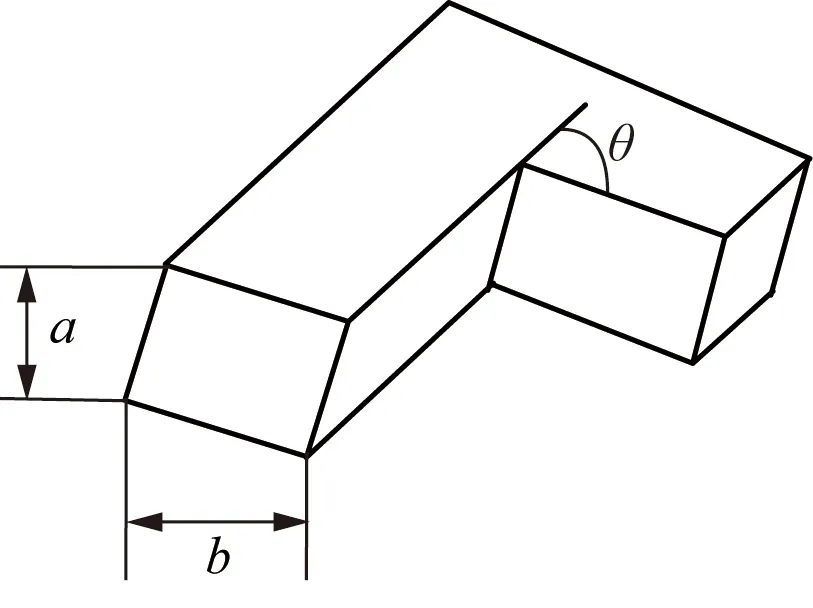
图5 不带盲管的锐角边弯管Fig.5 Acute angle bending pipe without blind tube

弯管中的阻力系数与流体雷诺数、管壁相对粗糙度、转角θ及相对曲率半径等因素有关。弯管总阻力系数ζ为摩擦阻力系数ζTP与局部阻力系数ζM之和[5]：

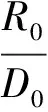
(1)

ζ=κΔκReCAζM(0°<θ<180°).

(2)

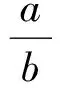
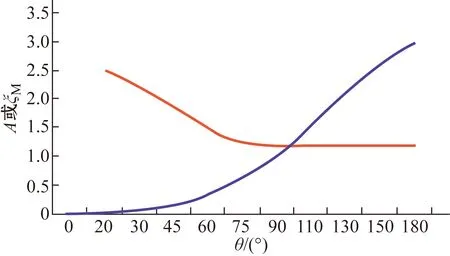
图6 A和ζM的值Fig.6 Values of A and ζM

对于带盲管的锐角边粗糙壁弯管，阻力系数的计算公式为

ζ1=1.2ζ=1.2κΔκReCAζM(0°<θ<180°).

(3)

因此，总阻力系数可近似用以下公式表示：

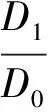
(4)

(5)

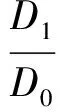
在油管悬挂器中，φ与θ为互余的关系，由式(4)和式(5)计算可得到ζ0与θ的关系，如图7所示；进而可以得到ζ0与φ的关系，如图8所示。

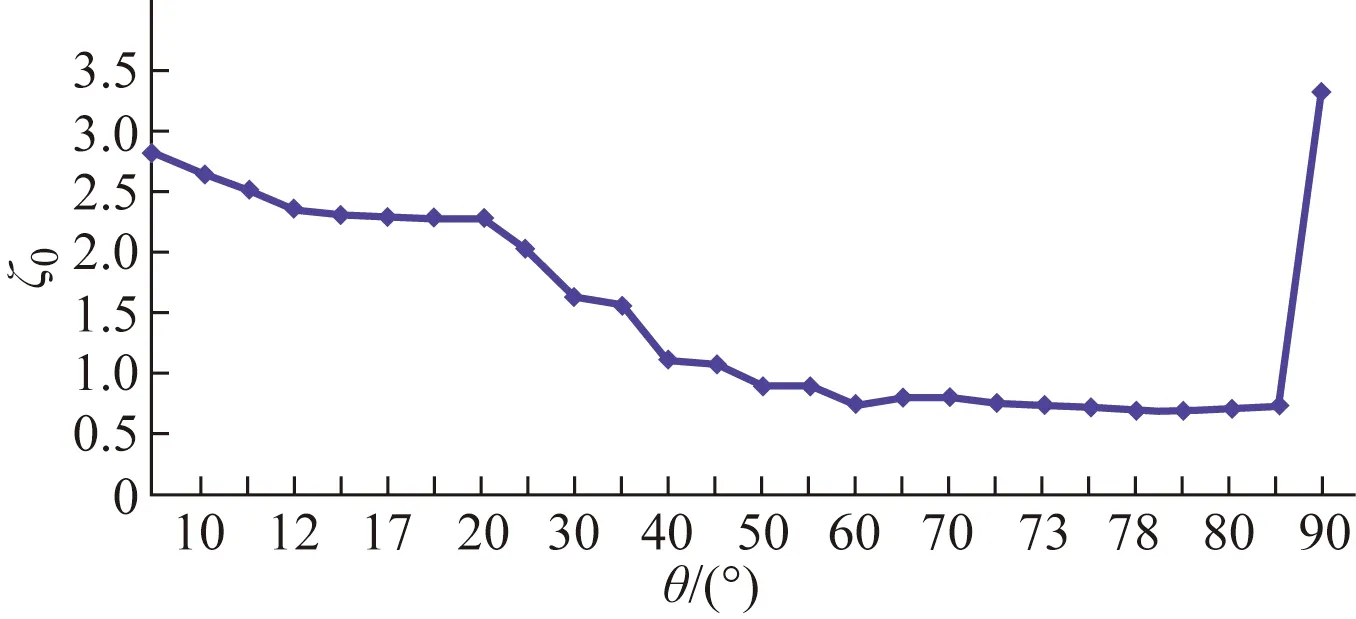
图7 ζ0与θ的关系Fig.7 Relation between ζ0 and θ

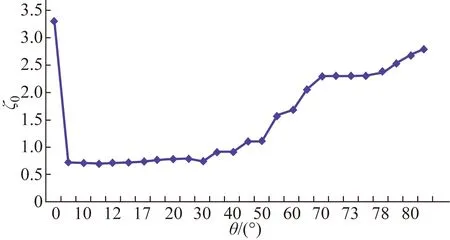
图8 ζ0与φ的关系Fig.8 Relation between ζ0 and φ

从图7可以看出，当角度θ为78°(与垂直方向的角度差)时，总阻力系数最小，流动最顺畅，即当油管挂出油口角度为12°(与水平方向的角度差)时，油管挂结构最佳。

3 油管挂出油口角度的数值模拟

在水下卧式采油树研究的初期，没有确定的理论模型或者公式来分析其内部流动情况，因此，需要借助模拟软件对水下卧式采油树及其组成部件内部流体的流动特性进行模拟，从而优化水下卧式采油树过流部件——油管悬挂器的设计方案。本文采用FLUENT软件，分别对不同出油口角度(0°、8°、10°、11°、12°、15°、17°、18°、20°、25°、30°和35°)下的油管悬挂器内部流动情况进行数值模拟研究，以验证油管挂出油口角度优化设计理论推导的结果。下面分别介绍数值模拟的物理模型、边界条件、网格划分和计算结果。

针对举升到同一水平位置的不同出油口角度进行数值模拟，其物理模型如图9所示。其中，油管悬挂器的内径为115 mm，高度为1.5 m，出油口直径为102 mm，出油口水平通道距油管挂底部高度为1 m。

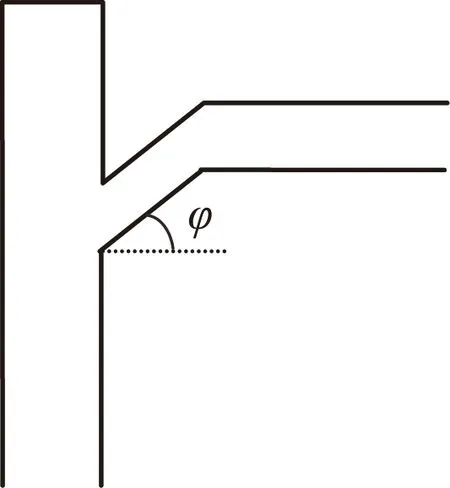
图9 物理模型Fig.9 Physical model

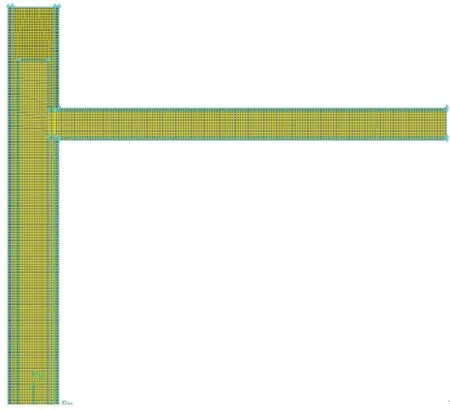
图10 油管悬挂器的网格划分Fig.10 Meshing of the tubing hanger

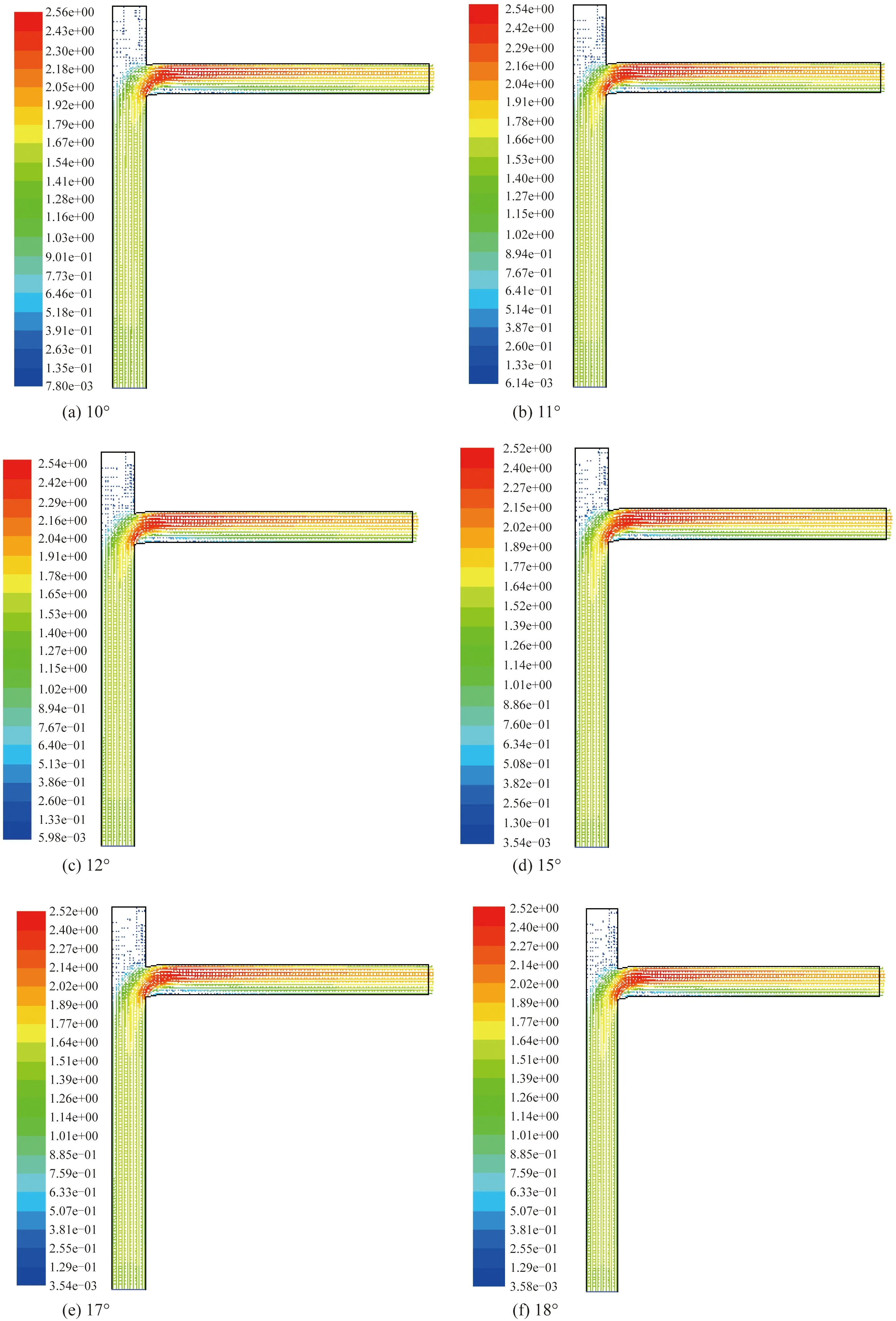
图11 速度矢量图Fig.11 Velocity vector

在油管挂的计算模型中，底面定义为速度入口“VELOCITY_INLET”，速度为1.5 m/s；右侧出油管出口定义为流体出口“OUTFLOW”，其余边设置定义为“WALL”。

油管挂的网格划分如图10所示，采用Tet/Hybrid四面体网格形式。

对出油口角度分别为0°、8°、10°、11°、12°、15°、17°、18°、20°、25°、30°和35°共12种工况下油管悬挂器内的流动情况进行数值模拟计算，得到不同出油口角度下的水平出油口处平均速度，结果如表1所示。

以出油口角度为10°、11°、12°、15°、17°和18°为例，它们的速度矢量图如图11所示。根据表1结果绘制出图12。

弯管的流动损失可以看做是在一段长度为l的管路中由沿程摩擦阻力造成的，如下式所示[6]：

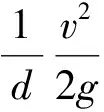
(6)

式中：λ为沿程摩阻系数，与雷诺数和管壁粗糙度有关；d为管道内径；v为管道有效截面上的平均速度。在油管悬挂器中，沿程摩阻系数为一定值，由式(6)可知，当平均速度越大时，弯管的流动损失越大，则压力损失越大。从表1和图12可以看出：当出油口角度为11°(与水平方向角度差)时，平均速度最小，即压力损失最小。因此，数值模拟的结果表明出油口的最优角度为11°。综合考虑基于阻力系数法的计算结果，油管悬挂器最佳的出油口角度应在11～12°之间。

表1 不同出油口角度下的计算结果Table 1 Calculation results for different outlet angles

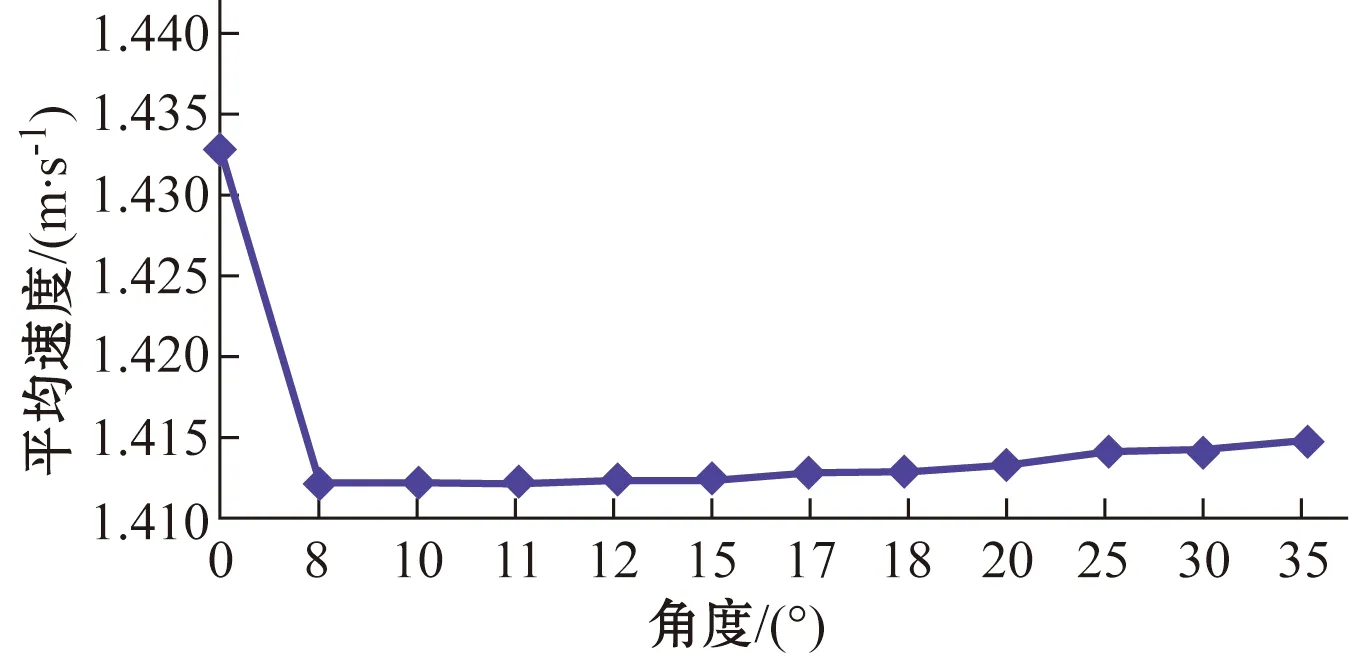
图12 不同出油口角度下的平均速度Fig.12 Average speeds for different outlet angles

4 结 语

通过对油管挂出油口角度设计的理论研究和数值模拟，取得下述成果：

(1) 水下卧式采油树油管挂出油口角度的优化设计可以采用阻力系数法。

(2) 对油管悬挂器内部流动情况的数值模拟结果表明，当出油口角度为11°时为最优角度。综合考虑阻力系数法的计算结果，油管悬挂器出油口角度在11°～12°之间时流动损失最小，即此时角度最佳。同时，在油管悬挂器的加工制造中，需将拐角处做圆滑处理，使阻力进一步降低。

[1] Eric D, Larson P E, Kevin G K. Marginal subsea development with existing subsea trees[C]. OTC, 2004：16533.

[2] Lafitte J I, Perrot M, Lesgent J, et al．Dalia subsea production system：presentation and challenges[C]. OTC, 2007:18541.

[3] Picciani F, Luce R. North Bardawil development project[C]. SPE, 2010:130281.

[4] ABB. HT subsea horizontal tree general presentation[R]. 2008.

[5] 华绍曾,杨学宁.实用流体阻力手册[M].北京:国防工业出版社，1985.

[6] 杨莜蘅,张国忠.输油管道设计与管理[M].东营:石油大学出版社,1996.

OptimizationDesignofTubingHangerOutletAngleofHorizontalTree

QIN Rui1, LI Qing-ping1, LUO Xiao-lan2, DUAN Meng-lan2

(1.CNOOCResearchInstitute，Beijing100028，China; 2.OffshoreOil/GasResearchCenter，ChinaUniversityofPetroleum，Beijing102249，China)

Aiming at the engineering problem of flow loss, an optimization design method of tubing hanger outlet is proposed on the basis of drag coefficient method, which considers the structural characteristics of tubing hanger, as well as the position and function of tubing hanger. By using the FLUENT software, a finite element model for tubing hanger is developed and the fluid flow in the tubing hanger is simulated. The results obtained by the drag coefficient method and the numerical results show that the best tubing hanger outlet angle is between 11° and 12°.

subsea pipeline; horizontal tree; tubing hanger; outlet angle; optimal design

TE973.92

A

2095-7297(2015)01-0050-05

2014-09-29

国家科技重大专项(2011ZX05026-004)、国家863计划(2012AA09A205)

秦蕊(1985—)，女，博士，主要从事海洋石油设施的设计方法与理论方面的研究。