关于双曲函数的Cusa-Huygens型不等式的改进

何灯，李云杰

(福清第三中学，福建福清350315)

关于双曲函数的Cusa-Huygens型不等式的改进

何灯，李云杰

(福清第三中学，福建福清350315)

本文将双曲函数的Cusa-Huygens型不等式作了进一步的改进，所建立的双边不等式优于现有的诸多结果，文末导出一条涉及算术平均、几何平均、对数平均的不等式链.

双曲函数；Cusa-Huygens型不等式；Seiffert平均；不等式

0 引言

文献[1-2]建立了著名的Cusa-Huygens不等式，文献[3]给出了双曲函数的Cusa-Huygens不等式，针对文献[3]所建立的不等式的改进与推广，现有诸多结果[4-13].本文研究sh x/x更优的上下界形式，从而可将双曲型Cusa-Huygens不等式作进一步的推广和改进，并由此建立了涉及算术平均、几何平均、对数平均的一条不等式链.

1 预备知识

Cusa-Huygens不等式[1-2]：设，则有.

双曲函数的Cusa-Huygens不等式[3]：设x∈（0，+∞），则有

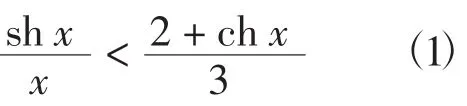
朱灵[7]将式（1）推广为：设x>0，，则有.

E.Neuman与J.Sándor改进式（1）为：设x>0，则.

成立当且仅当q≥3.

朱灵[15]将式（2）推广为：设x>0，p>1或p≤8/15，则当且仅当q≥3（1-p）.特别地，令p＝1/2，q=3/2，可得

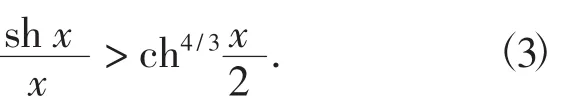
杨镇杭[11]将式（3）推广为：

最近，杨镇杭[16]证得如下两个结论：

结论1设p，x＞0，双边不等式

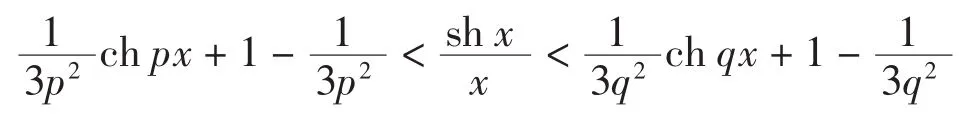
结论2设x＞0，则

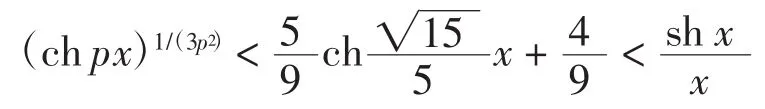
综合上述结论，可得不等式链

2 引理及证明

引理1设n∈N*，n≥7，则22n＞（1+p）2n+0.57n（1+p）2n，其中（下同）.

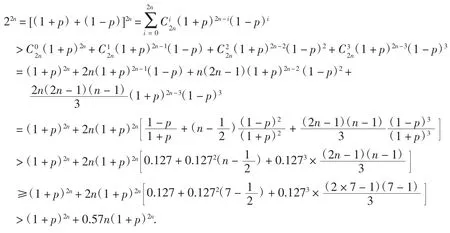
引理2设an=89×22n+121-（2n+1）[25（1+p）2n+25（1-p）2n+34+75p2n]，n∈N*，则an≥0.

证明当n＝1，2，3，可求an＝0.可求.

当n≥7，由引理1得

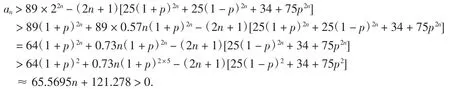
综上，引理2成立.

3 主要结论及其证明

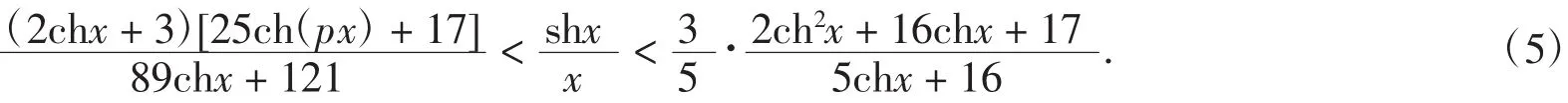
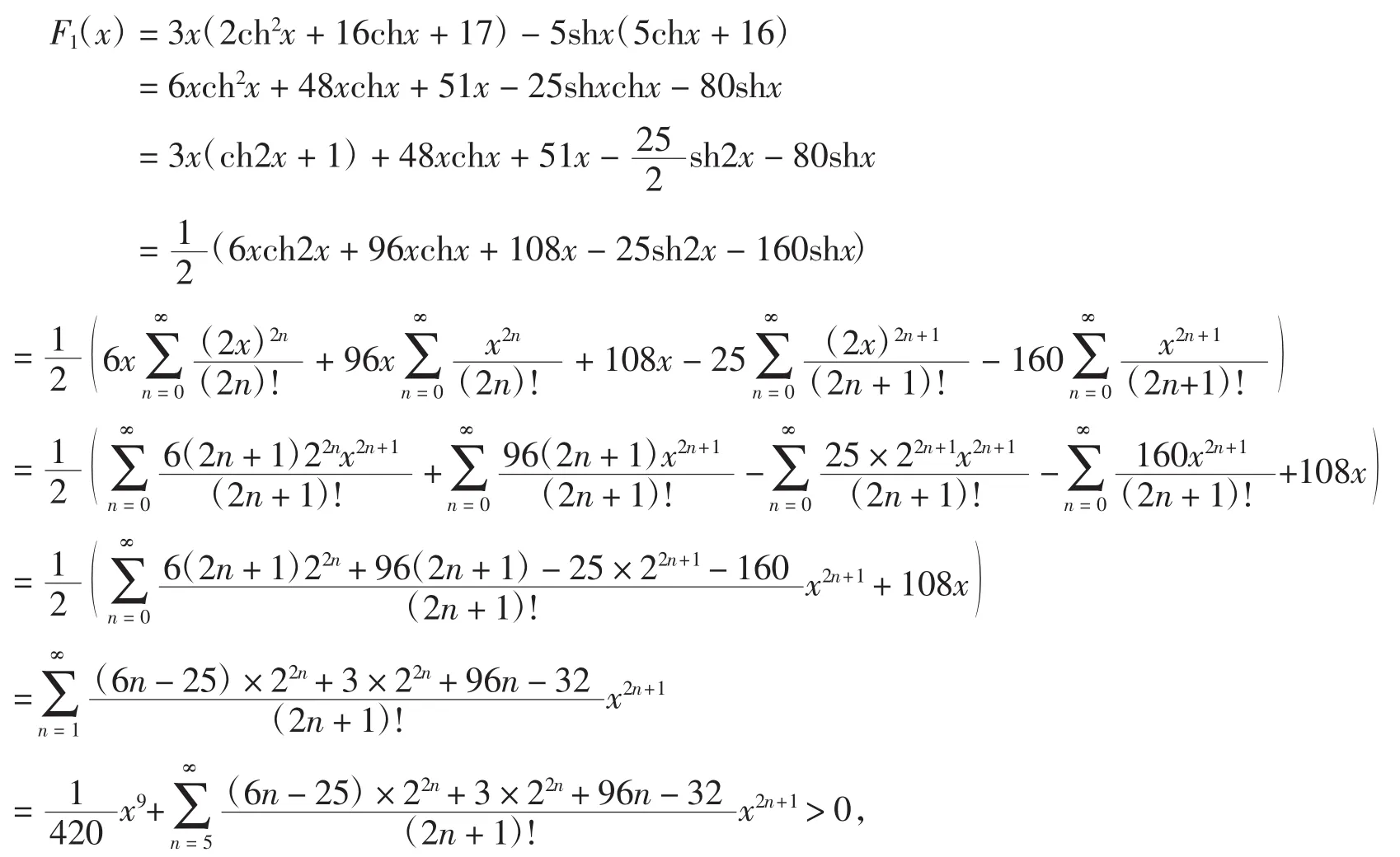
从而式（5）右端不等式成立.又

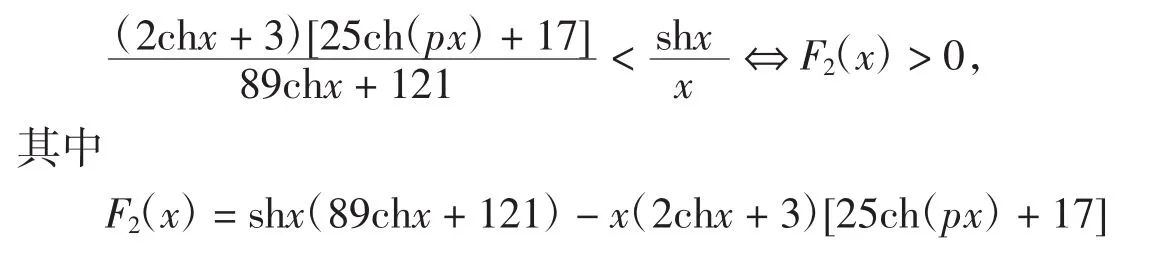
由引理2可证最后一个不等式成立，则有式（5）左端不等式成立.

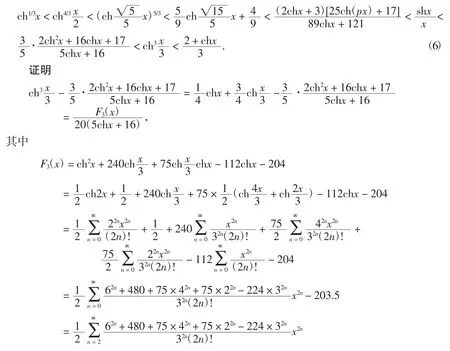
结合式（4），可得式（6）成立.

4 定理2的等价形式

两个正数a，b的幂平均定义为[17]

A2，A1，A0分别称为这两个数的平方根平均，算术平均及几何平均.

四类Seiffert平均分别定义为

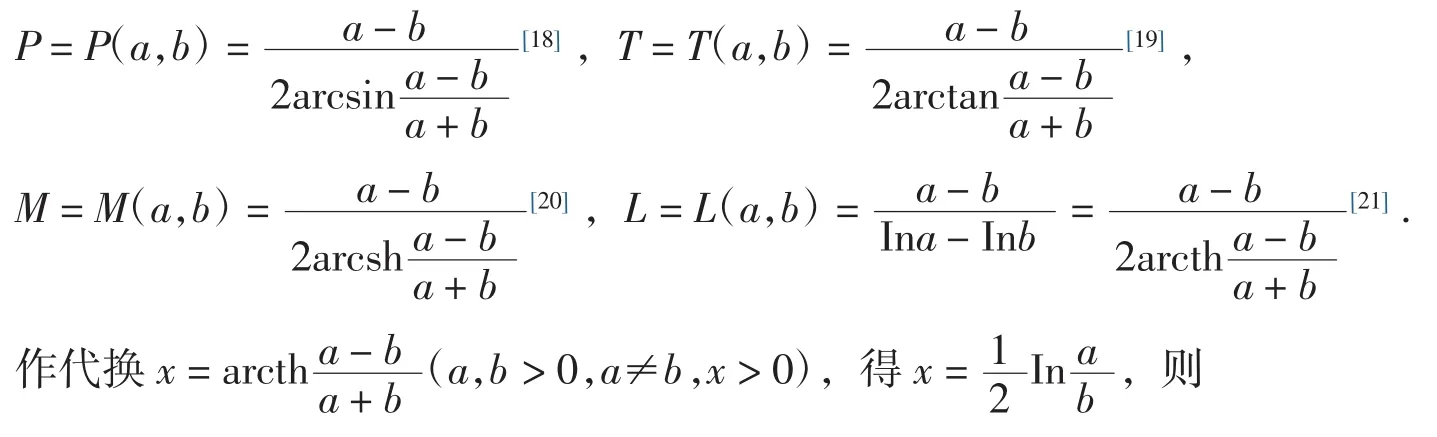
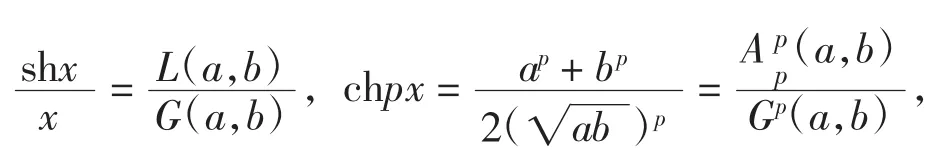
从而定理2等价于下定理3.

定理3设a，b>0，a≠b，则如下不等式链成立

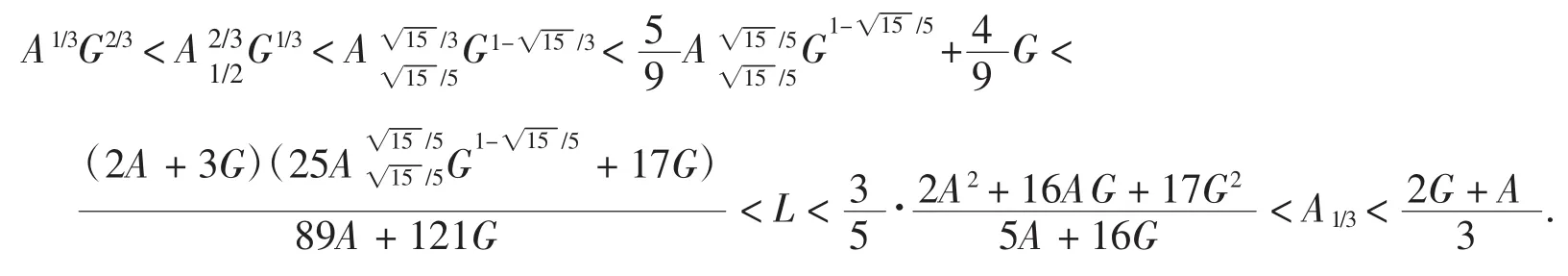
[1]Cajori F.A history of mathematics[M].2nd ed，New York：BibioLife，1929.

[2]Campan F T.The story of number[M].Romania：Ed Albatros，1977.

[3]Neuman E，Sándor J.On some inequalities involving trigonometric and hyperbolic functions with emphasis on the Cusa-Huygens，Wilker and Huygens inequalities[J].Math Inequal Appl，2010，13（4）：715-723.

[4]Zhu L.New inequalities for means in two variables[J].Math Inequal Appl，2008，11（2）:229-235.

[5]Zhu L.Some new inequalities for means in two variables[J].Math Inequal Appl，2008，11（3）：443-448.

[6]Zhu L.Some new inequalities of the Huygens type[J].Comput Math Appl，2009，58（6）：1180-1182.

[7]Zhu L.Inequalities for hyperbolic functions and their applications[J/OL].J Inequal Appl，2010. [2013-10-10].http://www.journalofinequalitiesandapplications.com/content/2010/1/130821.

[8]Neuman E，Sándor J.Inequalities for hyperbolic functions[J].Appl Math Comp，2012，218（18）：9291-9295.

[9]Wu S H，Debnath L.Wilker-type inequalities for hyperbolic functions[J].Appl Math Lett，2012，25（5）：837-842.

[10]Zhu L.New inequalities for hyperbolic functions and their applications[J/OL].J Inequal Appl，2012.[2013-10-20].http://www.journalo?nequalitiesandapplications.com/content/2012/1/303.

[11]Yang Z H.New sharp bounds for logarithmic mean and identric mean[J/OL].J Inequal，Appl，2013. http://www.journalo?nequalitiesandapplications.com/content/2013/1/116.

[12]Chen C P，Sándor J.Inequality chains for Wilker，Huygens and Lazarevitype inequalities[J].J Math Inequal，2014，8（1）：55-67.

[13]Yang Z H.Three families of two-parameter means constructed by trigonometric functions[J/OL].J Inequal Appl，2013.[2014-1-10].http://www.journalofinequalitiesandapplications.com/content/2013/1/541.

[15]Zhu L.Generalized Lazarevic’s inequality and its applications-Part II[J/OL].J Inequal Appl，2009. [2014-1-20].http://www.journalofinequalitiesandapplications.com/content/2009/1/379142.

[16]Yang Z H，Chu Y M.Jordan type inequalities for hyperbolic functions and their applications[J/OL]. Journal of Function Spaces.2014.[2014-3-10].http://www.hindawi.com/journals/jfs/aip/370979/.

[17]匡继昌.常用不等式[M].第四版.济南：山东科学技术出版社，2010.

[18]Seiffert H J.Werte zwischen dem geometrischen und dem arithmetischen Mittel zweier Zahlen[J]. Elemente der Mathematik，1987，42（4）：105-107.

[19]Seiffert H J.Aufgabe 16[J].Die Wurzel，1995，29：221-222.[20]Neuman E，Sándor J.On the Schwab-Borchardt mean[J].Math Pannon，2003，14（2）：253-266.

[21]Neuman E.Bounds for symmetric elliptic integrals[J].J Approx Theory，2003，12（2）：249-259.

Im provement of Cusa-Huygens Type Inequality for Hyperbolic Functions

HE Deng，LI Yunjie
（Number 3 Middle School，Fuqing 350315，Fujian，China）

In this paper，Cusa-Huygens type inequalities for Hyperbolic Functions are improved.The double inequality is obtained.An inequality chain about arithmetic mean，geometric mean，logarithmic mean is derived.

Hyperbolic functions；Cusa-Huygens type inequality；Seiffert mean；inequality

O 178

A

1001-4217（2015）02-0028-07

2014-09-08

何灯（1984-），男，福建福清人，学士，全国不等式研究会成员.研究方向：解析不等式及不等式机器证明.E-mail：hedeng123@163.com.