钢管混凝土抗震性能ABAQUS数值模拟中损伤因子比较研究

黄 宏，林博洋，陈梦成

（1.华东交通大学土木建筑学院，江西 南昌330013；2.江西省建筑过程模拟与控制重点实验室，江西 南昌330013）

钢管混凝土抗震性能ABAQUS数值模拟中损伤因子比较研究

黄 宏1，2，林博洋1，2，陈梦成1，2

（1.华东交通大学土木建筑学院，江西 南昌330013；2.江西省建筑过程模拟与控制重点实验室，江西 南昌330013）

针对国内外3种不同的混凝土损伤计算模型，分别用其模拟计算了往复荷载下钢管混凝土损伤过程，并绘出了3种模型损伤因子随应变变化的曲线；对于Birtel和Mark模型，探讨了系数bc对损伤因子的影响，随着系数bc取值的减小，相同应变下对应的损伤因子值增大；最后将这3种模型有限元计算得到的往复荷载下钢管混凝土构件的骨架曲线与试验骨架曲线进行对比分析。比较结果表明：当Birtel和Mark模型中bc取0.5时，计算得到的荷载（P）-位移（Δ）骨架曲线与试验结果误差最小，基于高斯积分算法的余能模型算出的骨架曲线与试验结果误差其次，修正的余能模型算出的骨架曲线与试验结果误差最大。

钢管混凝土；往复荷载；ABAQUS软件；混凝土损伤因子

随着有限元理论的不断发展，结合计算机技术，出现了许多通用有限元分析软件，如ABAQUS、ALOGR、ANSYS、NASTRAN、MARC、LS-DYNA。有限元分析软件ABAQUS具有非常强大的非线性分析功能，其被广泛的应用于土木工程结构计算中，ABAQUS中的混凝土塑性损伤模型是根据Lubliner[1]和Lee，Fenves[2]提出的混凝土损伤模型建立的，它们常通过引入损伤因子来描述混凝土的损伤行为，因此损伤因子的计算对于钢管混凝土抗震性能的模拟有着很关键的作用。

目前国内外已有学者基于连续介质力学和不可逆热力学提出了混凝土损伤本构模型，如Kachanov损伤模型、Loland受拉损伤模型、Mazars损伤模型、Sidoroff损伤模型、Krajcinovic损伤模型、随机受压损伤本构模型等，但这些模型均是在静荷载作用下提出的，对于像往复荷载作用下的钢管混凝土损伤模拟，大部分模型都不适用。

本文对ABAQUS计算中常见的国内外模拟往复荷载作用下3种不同的混凝土塑性损伤计算模型进行简要的介绍，然后分别用其对钢管混凝土抗震性能骨架曲线进行模拟，并做对比分析。

1 混凝土塑性损伤计算模型

1.1 基于余能原理的混凝土塑性损伤模型

孙从亚等根据Najar损伤理论，从能量耗散的角度提出了一种混凝土单轴受压塑性损伤模型，并在混凝土损伤变量d的积分计算中采用了高斯积分法[3]。

如图1所示，根据Najar损伤理论，损伤变量定义为

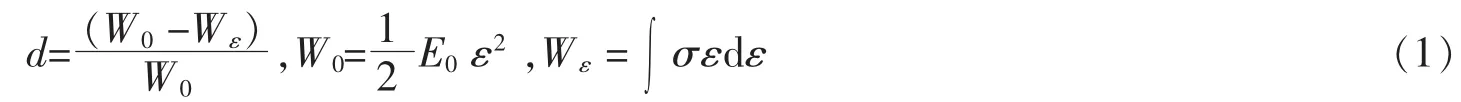
其中：W0为无损状态应变能；Wε为损伤状态下应变能；σ，ε分别为损伤状态对应的应力和应变；Eo为混凝土初始弹性模量。

Najar在计算Wε时进行了线性简化，即Wε=σε/2。国内学者在计算Wε则采用了高斯积分法，精度相对得到了改善。徐超[4]采用王中强，余志武[5]提出的Wε辛普森积分算法，模拟计算往复荷载下薄壁钢管混凝土柱的滞回曲线，并于试验结果对比，二者吻合程度良好。

1.2 修正的基于余能原理的混凝土塑性损伤模型

1.1节模型在计算混凝土无损伤状态下W0时，认为应力与应变始终是无限线性增长的，也即混凝土不存在破坏极限强度。刘杰等认为这不符合混凝土实际情况，在计算W0时应该考虑塑性变形的吸能和耗能能力[6]。图2给出了刘杰的修正模型示意图，该模型认为混凝土在达到极限强度之前无损伤状态下的应力-应变关系保持线性增长，达到极限强度之后，其应力保持不变。

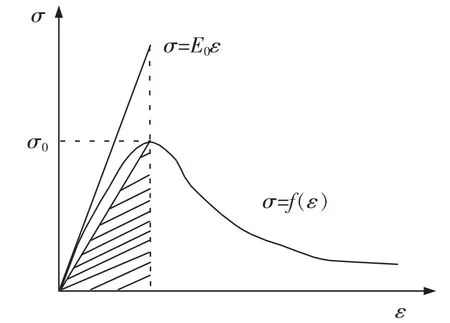
图1 Najar线性损伤模型Fig.1 Najar linear damage model

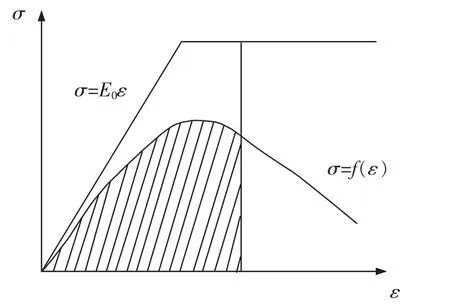
图2 修正的损伤模型Fig.2 Emended damage factor calculation principle

1.3 Birtel和Mark模型

Birtel和Mark[7]根据Krtzig W B，Plling R[8]的弹塑性损伤模型通过引入系数bc（t）计算损伤因子

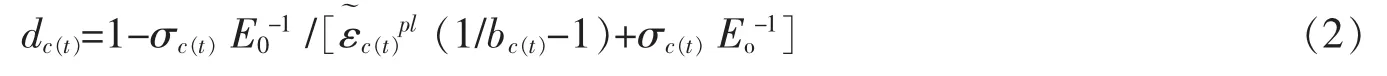
2 损伤因子随应变变化规律对比

根据刘威[10]提出的钢管混凝土中核心混凝土应力-应变关系模型，应用上述三种混凝土塑性损伤模型计算出受压损伤因子dc随压应变εc的变化关系曲线，如图3所示。

在应用Birtel和Mark模型计算损伤因子时，考虑到混凝土受拉对往复荷载下钢管混凝土的抗震性能影响较小，我们在图3中只给出了bc=0.5，0.7，0.9时受压损伤因子dc与压应变εc关系曲线，以考察取值对关系曲线变化规律的影响。从图3中可以看出，基于余能原理模型和修正的基于余能原理模型在混凝土达到极限强度之前损伤因子随应变的关系曲线是重合的，道理很简单，它们在计算W0时，无损伤状态下应力和应变均为线性关系，达到极限强度后，二者出现明显的差别。对于Birtel和Mark模型来说，当bc取0.5或0.7时，计算得到的损伤因子和基于余能原理模型计算出的损伤因子相差不大，但当bc取0.9时，其差别较为明显。

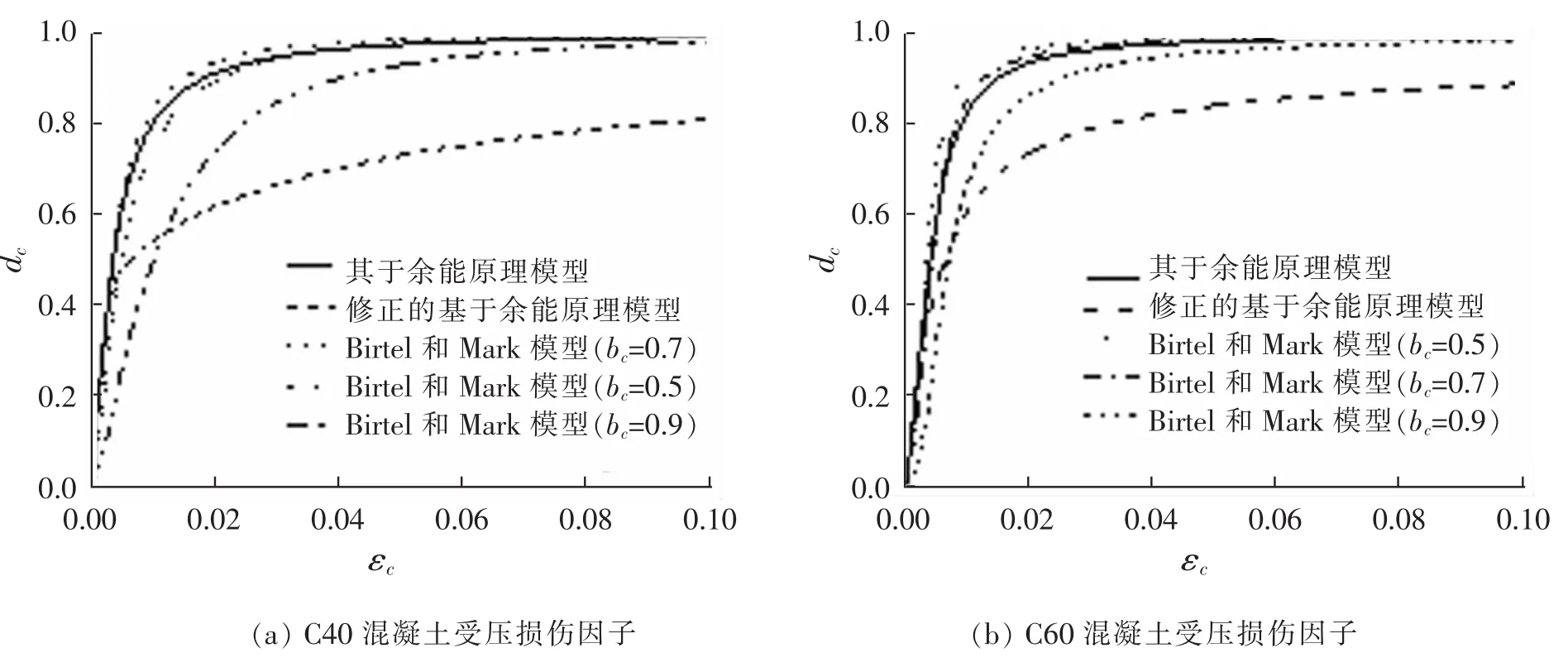
图3 混凝土损伤因子与应变关系曲线对比Fig.3 Comparison of damage factor and strain curve

3 实例对比分析

3.1 实例简介

本文实例采用文献[11]中的试验研究中的4个试件，试件编号分别为dcc1-1，dcc2-1，dsc1-1，dsc2-1。

3.1.1 圆实心钢管混凝土试件（dcc1-1）

该试件长度L=1 500 mm，钢管直径D=114 mm，厚度t=3 mm，钢管屈服强度fyo=308 MPa，混凝土标准立方体抗压强度fcu=38.9 MPa，轴向力N0=0 kN。

3.1.2 圆中空夹层钢管混凝土试件（dcc2-1）

该试件长度L=1 500 mm，外钢管直径D0=114 mm，厚度t0=3 mm，内钢管直径Di=32 mm，厚度ti=3 mm，外钢管屈服强度fyo=308 MPa，内钢管屈服强度fyi=422.3 MPa，混凝土标准立方体抗压强度fcu=38.9 MPa，轴向力N0=0 kN。

3.1.3 方实心钢管混凝土试件（dsc1-1）

该试件长度L=1 500 mm，钢管直径B=120 mm，厚度t=3 mm，钢管屈服强度fyo=275.9 MPa，混凝土标准立方体抗压强度fcu=58.1 MPa，轴向力N0=0 kN。

3.1.4 方中空夹层钢管混凝土试件（dsc2-1）

该试件长度L=1 500 mm，外钢管直径B0=120 mm，厚度t0=3 mm，内钢管直径Di=32 mm，厚度ti=3 mm，外钢管屈服强度fyo=275.9 MPa，内钢管屈服强度fyi=422.3 MPa，混凝土标准立方体抗压强度fcu=58.1 MPa，轴向力N0=0 kN。

3.2 建模方法

采用有限元分析软件ABAQUS建立模型，对于混凝土的受压应力-应变关系模型采用刘威[10]提出的适用于有限元分析计算的本构关系模型，对于往复荷载下的混凝土，还需输入损伤因子与混凝土非弹性应变的数值，用来计算混凝土往复荷载下卸载刚度的降低，损伤因子的取值则采用上述的三种混凝土塑性损伤模型进行计算。对于混凝土的受拉性能，考虑到建模的工作量及收敛性，本文采用ABAQUS提供的断裂能-开裂位移接口来定义，即直接输入断裂能[12]，ABAQUS混凝土塑性损伤模型除了考虑由于拉压塑性应变导致的卸载刚度的退化外还考虑了循环荷载下的刚度恢复，对于钢管混凝土[13]，取ωc=0.2，ωt=0。

循环荷载下的钢材本构模型采用ABAQUS软件自带的双线性随动强化模型，该模型能够反映包兴格效应，并且考虑了各向同性强化和随动强化准则，其强化阶段的弹性模量取0.01 Es，Es为钢材初始弹性模量。

钢管混凝土压弯构件往复荷载作用下的边界条件是两端铰支，中间施加横向往复荷载。由于其结构和受力的对称性，本文采用半构件模型进行计算，半构件模型的边界条件是一端固定一端自由。

钢管采用壳单元（S4R），混凝土采用三维实体单元（C3D8R），采用结构化网格划分技术。内外钢管和混凝土之间法向采用硬接触，切向采用库仑摩擦模型（摩擦系数μ=0.25），内外钢管与盖板之间采用壳-实体耦合。分析计算时采用位移加载，通过设置多个分析步，每一分析步中都定义了相应的位移，来实现构件的往复循环加载。

3.3 结算结果比较

为了能更清晰地看出3种损伤模型数值结果对比，本文只给出实例在3种损伤计算模型下的有限元计算骨架曲线与试验骨架曲线的对比，如图5～图8所示。

由图4（a），图5（a），图6（a），图7（a）可知：Birtel和Mark模型计算出的实例荷载（P）-位移（Δ）骨架曲线和试验骨架曲线最接近，并和基于余能原理模型计算出的骨架曲线相差不大，修正的基于余能原理模型计算出的骨架曲线承载力与试验相差最大，这是因为修正的基于余能原理计算的混凝土损伤程度最低。由图4（b），图5（b），图6（b），图7（b）可知：对于Birtel和Mark模型，随着系数bc取值的减小，计算出的荷载（P）-位移（△）骨架曲线承载力也降低。当bc=0.5时，计算骨架曲线和试验骨架曲线最为接近。

图4 试件dcc1-1有限元计算骨架曲线与试验骨架曲线对比Fig.4 Comparison of skeleton curve between experiment and FEA from dcc1-1

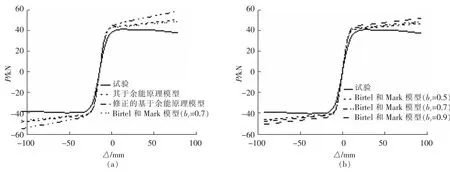
图5 试件dcc2-1有限元计算骨架曲线与试验骨架曲线对比Fig.5 Comparison of skeleton curve between experiment and FEA from dcc2-1

图6 试件dsc1-1有限元计算骨架曲线与试验骨架曲线对比Fig.6 Comparison of skeleton curve between experiment and FEA from dsc1-1

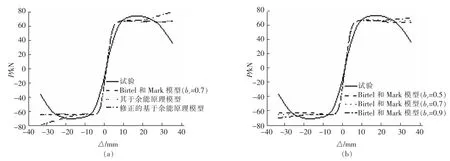
图7 试件dsc2-1有限元计算骨架曲线与试验骨架曲线对比Fig.7 Comparison of skeleton curve between experiment and FEA from dsc2-1

4 结论

通过以上对比分析，我们得出以下结论：

1）基于余能原理的混凝土损伤模型与修正的基于余能原理的混凝土损伤模型计算出来的损伤因子随应变的关系曲线在混凝土达到极限强度前是重合的，但此后，误差越来越大。对于Birtel和Mark模型来说，当bc取0.5或0.7时，计算出的损伤因子和基于余能原理的混凝土损伤模型得到的损伤因子误差不大，但当bc取0.9时，其误差别较明显。

2）当bc=0.5时，用Birtel和Mark模型计算出的实例荷载（P）-位移（Δ）骨架曲线与试验误差最小，并和基于余能原理的混凝土塑性损伤模型得到的骨架曲线相差不大，修正的基于余能原理的混凝土塑性损伤模型计算出的骨架曲线则与试验误差最大；对于Birtel和Mark模型，随着系数bc取值的减小，计算出的荷载（P）-位移（Δ）骨架曲线承载力也降低。

[1]LUBLINER J，OLIVER J，OLLER S，et al.A Plastic damage model for concrete[J].International Journal of Solids and Structures，1989，25（3）：299-326.

[2]LEE J，FENVES G L.Plastic damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics，1998，124（8）：892-900.

[3]孙从亚，逯静洲，王风达.基于高斯积分算法的混凝土损伤模型[C]//第17届全国结构工程学术会议论文集，武汉：中国力学学会，工程力学杂志社，2008.

[4]张耀春，徐超，卢孝哲.带肋薄壁方钢管混凝土柱的滞回性能[J].东南大学学报：自然科学版，2007，37（1）：100-106.

[5]王中强，余志武.基于能量损失的混凝土损伤模型[J].建筑材料学报，2004，7（4）：365-369.

[6]何小涌，刘杰.修正的混凝土塑性损伤因子及有效性验证[J].建筑结构，2014，44（S1）：488-492.

[7]BIRTEL V，MARK P.Parameterised finite element modeling of RC beam shear failure[C]//ABAQUS Users’Conference.Cambridge，USA，2006：95-108.

[8]KR TZIG W B，P LLING R.An elasto-plastic damage model for reinforced concrete with minimum number of material parameters [J].Computers and Structures，2004（82）：1201-1215.

[9]曲慧.钢管混凝土柱-钢筋混凝土梁连接节点抗震性能的机理分析[J].工程力学，2012，29（7）：235-243.

[10]刘威.钢管互混凝土局部受压时的工作机理研究[D].福州：福州大学，2005.

[11]HAN LINHAI，HUANG HONG，ZHAO XIAOLING.Concrete-filled double skin steel tubular(CFDST)beam-columns subjected to cyclic bending[J].Engineering Structures，2006，28（12）：1698-1714.

[12]黄宏，黄斌洁.圆中空夹层钢管混凝土纯扭构件工作机理研究[J].华东交通大学学报，2010，27（6）：1-6.

[13]黄宏，黄诚，陈梦成.方中空夹层钢管混凝土压弯构件滞回性能的有限元分析[J].铁道建筑，2010（7）：57-61.

Comparison Study on Damage Factor in ABAQUS for Seismic Simulation of Concrete Filled Steel Tube

Huang Hong1，2，Lin Boyang1，2，Chen Mengcheng1，2
(1.School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang 330013,China；2.Jiangxi Key Laboratory of Control and Simulation of Construction Process,Nanchang 330013,China)

Aiming at three different concrete damage computational models at home and abroad,the study utilized them to simulate the damage process of concrete-filled steel tube under cyclic loading respectively.The damage factor varying with strain for the three models was drawn.For Birtel and Mark model,the impact of coefficient in the model on the damage factor was also discussed.With the decrease of the coefficient,the damage factor increased under the same strain.Finally,the CFST skeleton curve of the FEM numerical solutions was compared with that of the test results under cyclic loading.It shows by the comparison that when in the Birtel and Mark modelit was 0.5,the load(P)-displacement(Δ)skeleton curve was in good agreement with the test results;the load（P)-displacement(Δ)skeleton curve by the complementary energy model had less errors,second to Birtel and Mark model compared to test results,but that of the modified complementary energy model had the largest errors in the three models.

concrete-filled steel tube；cyclic loading;ABAQUS software；concrete damage factor

TU398.9

A

1005-0523（2015）06-0061-06

(责任编辑 姜红贵)

2015－06-16

国家自然科学基金项目（51378206,51468017）；江西省青年科学基金计划（20143ACB21020）

黄宏（1977—），女，教授，博士，主要研究方向为组合结构。

陈梦成（1962—），男，教授，博士生导师，主要研究方向为工程结构材料耐久性。