摆式剪切机上刀架以及摆架的有限元分析
2015-12-08设计
设 计
郭志强 赵 霞
(内蒙古科技大学机械工程学院,内蒙古014010)
摆式剪切机上刀架以及摆架的有限元分析
设计
郭志强赵霞
(内蒙古科技大学机械工程学院,内蒙古014010)
摘要:通过对摆剪上刀架以及摆臂部位在4个最大工况点进行应力变形分析,得出摆剪上刀架以及摆架的应力集中部位和摆架滑道部位的变形量,并分析其在正反转过程中的不同,解释了摆剪在反转以后出现的问题。
关键词:摆式剪切机;摆架;应力;上刀架
本文研究的摆式剪切机是由某大型集团引进德国西马克公司技术制造的剪切机,之前摆剪一直是正转,但由于某些原因开始反转,此时上刀架在摆架滑道中出现变形以及磨损的现象,使摆式剪切机的运动过程不能按照正常要求运行,为此对摆式剪切机进行了有限元分析,分析在正反转过程中其应力变形情况有何不同。
1 摆式剪切机工作原理及受力分析
摆式剪切机的机构为双偏心曲柄滑块机构。图1是摆剪的结构受力图。AB为飞剪机的双偏心曲柄,AC为曲柄与上刀架本体间的连杆,BD为摆剪摆架。O点是曲柄的中心,A点是曲柄与连杆的铰接点,B点是曲柄摆架的铰接点,C点是连杆与滑块的铰接点,同时也是滑块与摆架BD的接触点,滑块(相对应上刀架的本体)在摆架BD上滑动。O2为摆剪摆动驱动的液压油缸,与O2O1为驱动臂。DO1为连接杆。D为剪切机构和摆动机构的连接点。在剪切过程中,双偏心曲柄AB以w的速度旋转、带动上剪刃本体和下剪刃本体上下往复动,实现剪切功能。而由于液压缸O2的驱动作用,连杆O1D带动摆架BD左右摆动,从而带动剪切机构摆动。下剪刀固定在摆架BD上,随其左右往复摆动,从而使上、下剪刃完成剪切,正反转亦如此。
以x轴、y轴为坐标轴,根据力平衡条件,力矩平衡条件建立方程组:
式中,FA是连杆的拉力;FB是摆架的压力;F为剪切力,F=8 500 kN;FN是摆剪上刀架对摆架滑道的侧压力;T是曲轴的转矩;P是主驱动的功率,P=450 kW;w是曲轴转速,w=1 500 r/min;R1是摆剪的上偏心量;R2是摆剪的下偏心量;γ是连杆与平行y轴方向的夹角;η是摆架与y轴的夹角。根据公式(1)~公式(4)可推出FN。
2 有限元模型的建立
2.1 模型的网格划分
由于摆式剪切机模型完全对称,为了减小运算量,方便网格的划分,减少计算时间,采取模型的一半作为研究的分析对象。模型的网格划分采用自由网格划分,划分网格节点数为177 054,划分单元数量为111 896,如图2所示。
摆剪的上刀架等各部分材料参数如表1所示。

图1 摆式剪切机机构受力简图
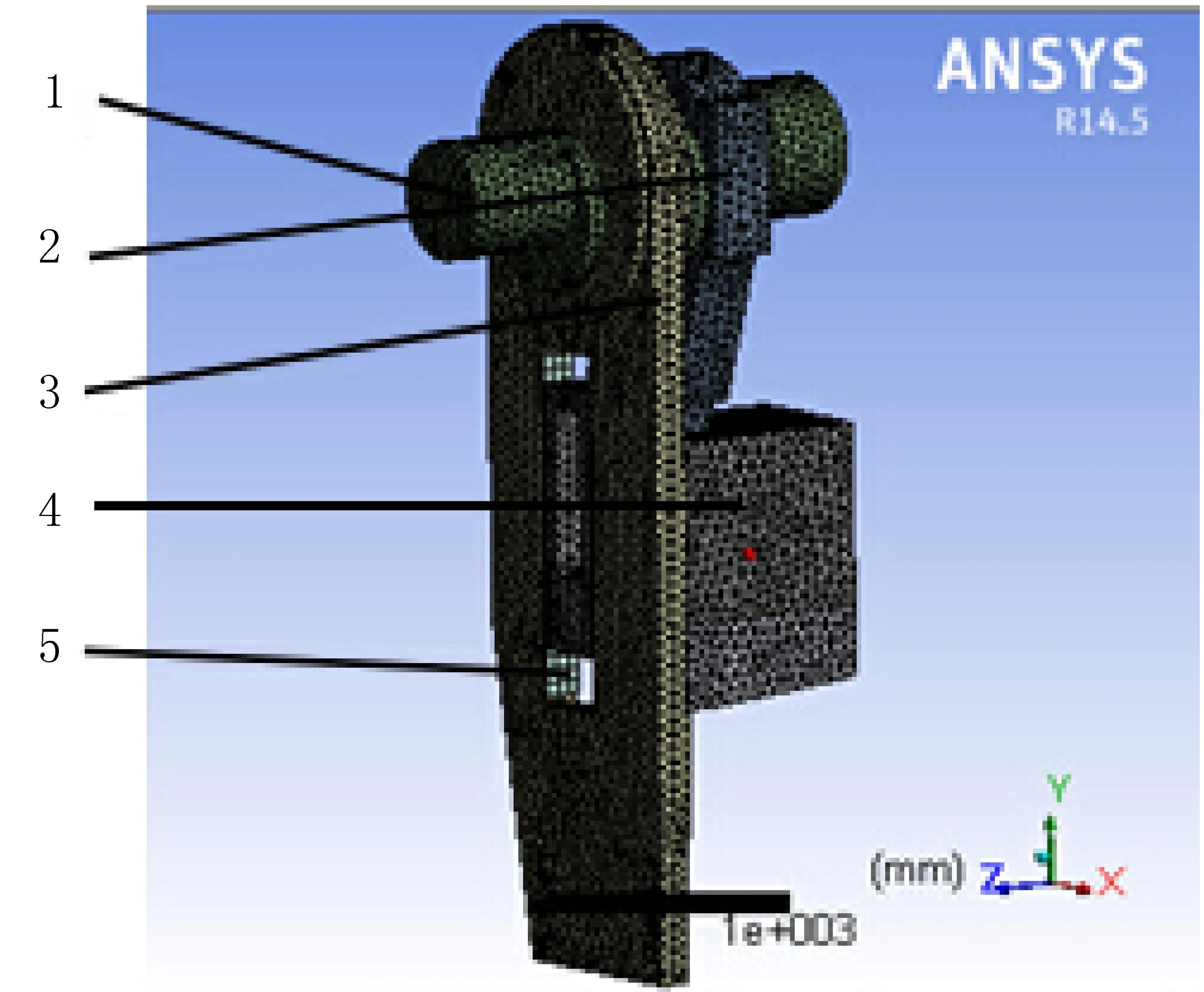
1—曲轴 2—连杆 3—摆架 4—上刀架 5—摆架滑道
2.2 载荷的施加以及边界条件的选取
选取4个特殊工况点研究摆剪的摆架以及上刀架部位的应力分析和变形。在这4个工况点,上刀架与摆架的侧压力最大,摆架上刀架应力变形也最大,这4个工况点分别是正、反转剪切开始时刻,曲轴转动77.77°,且剪切力为8 500 kN时;正、反转剪切结束时刻,曲轴转动292.23°,且无剪切力的作用时。
在这4个特殊工况点时要限制曲轴自由端x轴、y轴、z轴的移动,由于对称结构对曲轴的自由端施加固定约束,曲轴的另一端施加轴向和径向的位移约束,使得连杆与摆架在曲轴上不能有位移上的窜动。摆剪分别受到连杆的压力FA、摆架的压力FB以及上刀架受到摆架的侧压力FN。在4个工况点中,摆剪各部分载荷的施加如表2所示,并且在这4个不同的工况载荷过程施加的剪切力都为8 500 kN。
3 有限元分析结果
由图3~图6可看出,当曲轴转动了77.77°有剪切力作用的情况下,摆剪正转时摆剪的整体最大等效应力为198.9 MPa,大于摆剪反转时的最大等效应力183.25 MPa。而且从图中可以看出与正转时相比,在反转时曲轴与上刀架的应力不是很均匀,曲轴摆架应力较为集中。而在没有剪切力作用的情况下,整体最大等效应力正转只有0.799 MPa,反转也只有0.749 MPa。说明剪切力对于摆式剪切机的应力大小影响很大,因为在有剪切力作用时摆剪应力非常大。下面主要分析在有剪切力作用的情况下,正、反转摆剪的摆架与上刀架的应力分布情况以及变形情况。

表1 摆剪各部分的材料参数Table 1 Material parameters of swing beam shears components
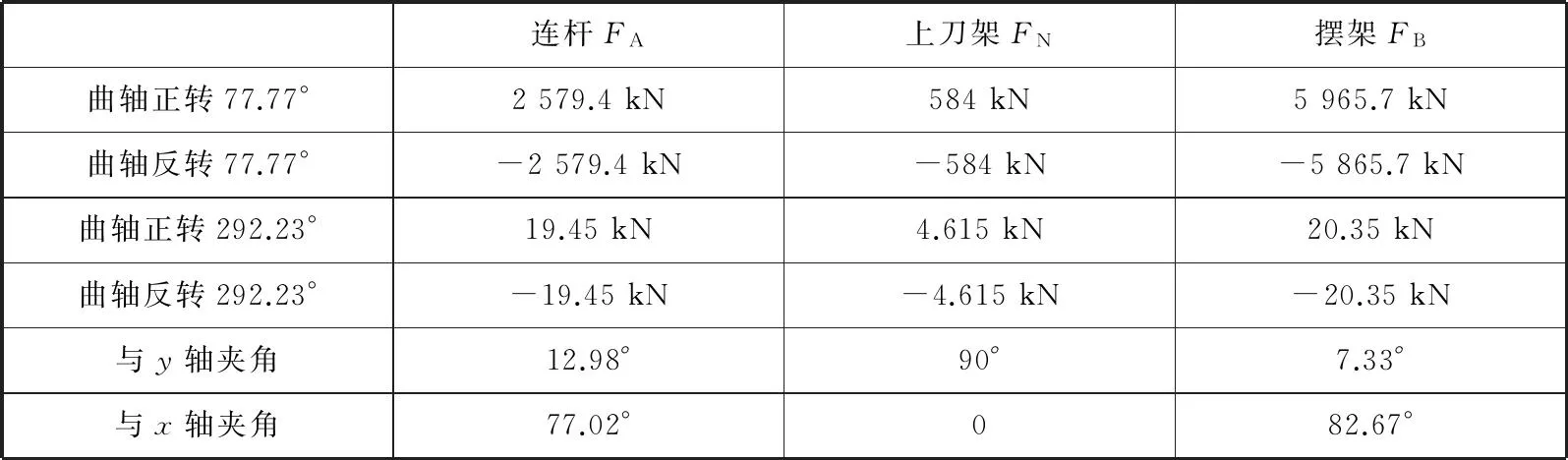
表2 摆剪各部分载荷施加表Table 2 Loading on swing beam shears components
从图7、图8可以看出,当曲轴转动77.77°时,正转摆架的最大等效应力为66.572 MPa,小于反转时的最大等效应力71.856 MPa。摆架滑道两侧的应力主要是由当摆剪在转到77.77°刚接触钢材时上刀架对摆架滑道产生的巨大的惯性力和冲击而导致的。正转时摆架右侧存在应力分布不均匀状况,而反转时摆架左侧应力存在不均匀状况。无论正转、反转,摆架滑道4个拐角部位都存在应力集中现象。为了减少应力集中的发生,有必要增大圆角半径。

图3 正转有剪切力作用时整体等效应力分布图

图4 反转有剪切力作用时整体等效应力分布图

图5 正转没有剪切力作用时整体等效应力分布图

图6 反转没有剪切力作用时整体等效应力分布图

图7 正转有剪切力作用时摆架的等效应力分布图

图8 反转有剪切力作用时摆架的等效应力分布图
如图9、图10所示,摆剪正转时上刀架的最大等效应力为73.857 MPa,大于反转时上刀架的最大等效应力68.432 MPa。正转时上刀架与摆架滑道部位相接处的下半部分应力比较集中,而反转时上刀架与摆架相接触的上半部分应力比较集中,说明由于转向的不同,上刀架与摆架接触部位的受力不同而导致应力分布不同。这就是摆剪在反转后上刀架与摆架滑道在接触部位(应力集中部位)会出现磨损的原因。

图9 正转有剪切力作用时上刀架的等效应力分布图

图10 反转有剪切力作用时上刀架的等效应力分布图

图11 正转有剪切力作用时摆架滑道变形位移图
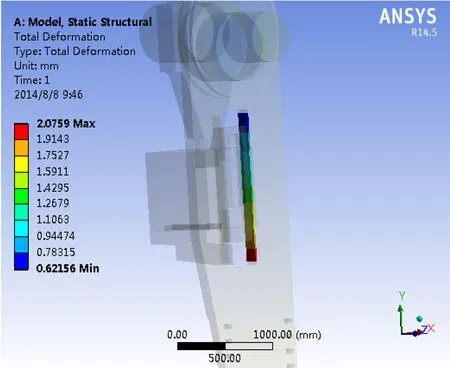
图12 反转有剪切力作用时摆架滑道变形位移图
从图11、图12可以看出,在有剪切力的作用时,摆剪滑道都是滑道下部的变形比较大,但是反转时滑道最大变形量2.075 9 mm比正转滑道变形量1.653 9 mm大。摆剪正转过程中变形偏滑道内侧,发生反转后变形偏滑道外侧。说明摆剪在正、反转的过程中,摆架滑道变形方向的不同可能导致因上刀架在滑道中二者相互接触不均匀、不协调而造成后来反转过程中的磨损变形。
4 结论
(1)通过对摆剪正、反转上刀架摆架的应力变形结果分析,摆剪各部分强度均符合标准,没有超过屈服极限。反转状态与正转状态相比,摆剪整体应力分布不均匀。
(2)摆剪正、反转上刀架的作用方向相反导致摆架滑道的变形方向不同,使摆剪的上刀架与摆架接触面出现应力集中。
(3)由于正反转摆架滑道的变形偏移量方向不同,使上刀架与摆架滑道接触不均匀而导致摆架滑道的磨损。
(4)分析结果证明了企业摆剪在使用过程中的问题,为企业维护设备提供理论依据。
参考文献
[1]邹家祥.轧钢机械[M].北京:冶金工业出版社,1989:234.
[2]刘海昌,汪建春,刘抗强.IH IR636 摆式飞剪测试与有限元分析[J ].机械设与制造,2007(08):11-13.
[3]F.aura, A.Garcia, M.Estremes. Finite element analysis of optimum clearance intheblanKingprocess[J].J.Mater.technology Process,1989,12(81): 121-125.
[4]夏建芳.IHI 摆式飞剪工作原理及剪切机构运动分析[J].中南工业大学学报,2001:12-14.
[5]牛贵玲,张九全,马美英.双偏心曲柄摆式飞剪机[J].重型机械, 2009(32):132-141.
编辑傅冬梅
Finite Element Analysis of Upper Tool Carrier and Swing
Arm of Swing Beam Shears
Guo Zhiqiang, Zhao Xia
Abstract:By analyzing on stress deformation of upper tool carrier and swing arm of swing beam shears at four maximum working condition points, stress concentration location of upper tool carrier and swing arm as well as deformation amount of slide have been worked out, and difference of corotation varying from inversion of swing beam shears have been analzed, meanwhile issues resulted from inversion have been illustrated.
Key words:swing beam shears; swing arm; stress; upper tool carrier
收稿日期:2014—09—03
中图分类号:TH132.4
文献标志码:A
