基因振子同步化的数值模拟

吴虞　高军晖

摘 要：Jordi Garcia-Ojalvo等人2004年在PNAS上发表了一篇文章，建立了多细胞基因共振的数学模型。该文对这个模型进行数值模拟，得到了同步化过程的实例，并研究Q值、细胞数量与同步化过程的关系。

关键词：基因振子 同步化过程 数值模拟 Q值

中图分类号：Q75 文献标识码：A 文章编号：1674-098X（2015）09（c）-0017-02

1 介绍

基因振子在多细胞之间能产生同步现象，是由于细胞外部环境的驱动力以及内部自我产生的节律。在论文[1]中，Jordi Garcia-Ojalvo等人研究了细胞中mRNA和蛋白质浓度随时间变化的动力学模型。该文对这个模型进行数值模拟，得到了同步化过程的实例，并研究Q值、细胞数量与同步化过程的关系。

2 方法

2.1 数学模型

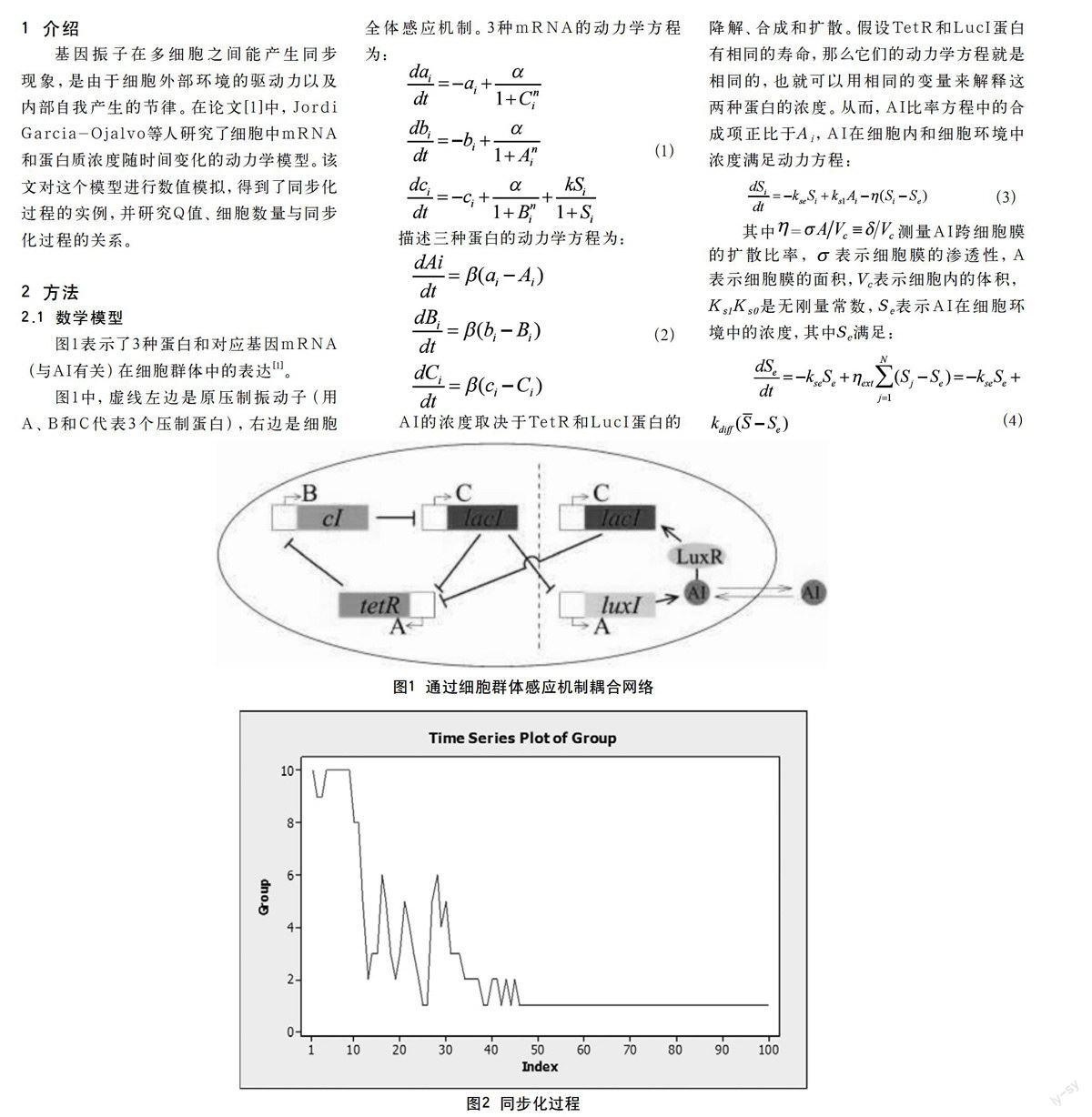
图1表示了3种蛋白和对应基因mRNA（与AI有关）在细胞群体中的表达[1]。

图1中，虚线左边是原压制振动子（用A、B和C代表3个压制蛋白），右边是细胞全体感应机制。3种mRNA的动力学方程为：

（1）

描述三种蛋白的動力学方程为：

（2）

AI的浓度取决于TetR和LucI蛋白的降解、合成和扩散。假设TetR和LucI蛋白有相同的寿命，那么它们的动力学方程就是相同的，也就可以用相同的变量来解释这两种蛋白的浓度。从而，AI比率方程中的合成项正比于Ai，AI在细胞内和细胞环境中浓度满足动力方程：

（3）

其中=测量AI跨细胞膜的扩散比率，表示细胞膜的渗透性，A表示细胞膜的面积，Vc表示细胞内的体积，Ks1Ks0是无刚量常数，Se表示AI在细胞环境中的浓度，其中Se满足：

（4）

当实际处理时，使为0，可以满足：

（5）

（6）

Q是刻画细胞密度（）的参数。

2.2 数值模拟结果

我们采用了论文中模拟的mRNA和蛋白质的动力学方程，固定了，，，以及N值和Q值。随机选取10个细胞，记录每一时刻的AI浓度。最终，10个细胞AI的浓度变化完全一致，达到同步状态。同步的过程由图2展示。

图2中的横轴表示时间点（步数），纵轴表示的是在这个时间点时AI浓度的变化分成了几组。可以看出，在大概0～50个时间点期间，分组数呈下降趋势，但有波动变化；在50个时间点以后，只有一组数据并不再出现变化，细胞完全同步了。

3 讨论

进一步，我们研究Q值、细胞数量与同步化过程的关系。

选取不同的N值，分别取N为1000000、500000、100000、50000、10000、5000，和不同的Q值，分别为0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1。不断重复上述的数值模拟过程，记录达到同步化的时间（步长），我们得到图3。

图3中，横坐标表示不同的Q值，纵坐标表示达到同步化需要的时间，不同颜色的6条曲线，代表了不同的N值。由图3可知，从0.8～0.5同步的速度是加快的，在0.5～0.3期间同步速度达到最大值，从0.3～0.1同步的速度又减缓了。

参考文献

[1] Jordi Garcia-Ojalvo， Michael B Elowitz，Steven H Strogatz，et al.Modeling a synthetic multicellular clock： Repressilators coupled by quorum sensing[J].PNAS，2004，101（30）：10955-10960.