一类具阻尼项的二阶半线性泛函微分方程的振动性

林文贤，郑伟珊

（韩山师范学院数学与统计学院，广东，潮州 521041）

讨论一类具阻尼项的二阶半线性中立型分布时滞泛函微分方程

(H4) μ(ξ)∈ C ([a,b],R) 为非减函数，方程（1）中的积分为Stieltjes 积分。

当 m (t)= 0 时，方程（1）就是文献[1]所研究的方程。本文的目的是建立方程（1）的 Leighton-Wintnertner型和Philos型振动准则，使得文[1-3]成为本文结果的特例，并且推广其他近期文献的一些振动结果。关于本文中的函数不等式，如果没有特别说明，都是对一切充分大的t成立。

1 主要结果

首先给出以下著名不等式。

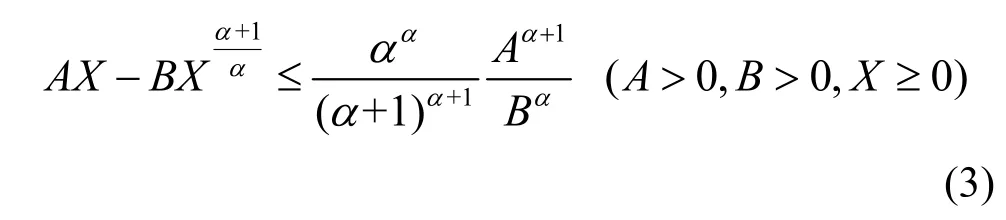
考 虑 集 合 D0= { (t,s) |t ＞ s ≥ t0}和D = { (t,s) |t ≥ s ≥ t0}，如果函数 H ∈ C (D,R)满足下列条件：

则称H是性质P。

首先，我们给出方程(1)的Philos型振动准则。

定 理 1 假 设 存 在 函 数 ρ (t) ∈ C1(I,R+) ,H(t,s)具有性质P， H (t,s) ∈ C (D0,R)使得

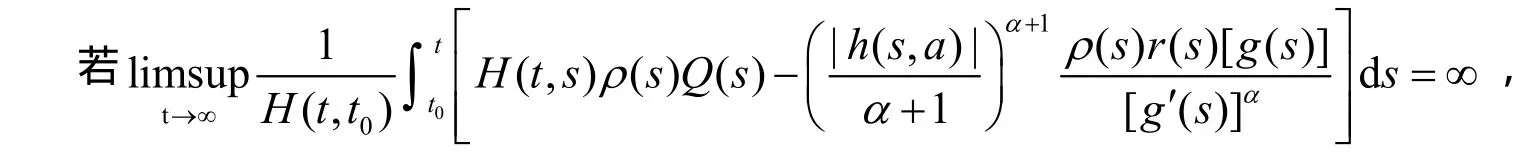
证明：设 x(t)是方程(1)的非振动解，不失一般性，可设 x (t) ＞ 0 ， t ≥t0。

令t→∞ ，由(H1)，有(t )=-∞ ， 这与y(t)＞0,t≥t1矛盾，所以y′(t) ＞ 0 ,t ≥ t1。

将（7）中的t换为s并两边同乘以 H (t,s)，在[t1,t]上关于s积分，得

矛盾。所以方程(1)是振动的。定理1证毕。

这就是方程(1)的 Philos型振动准则，下面再给出方程(1)的Leighton-Wintnertner型振动准则。

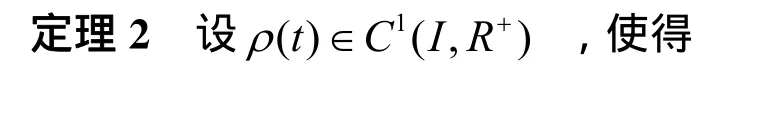
证明：设 x(t)是方程(1)的非振动解，不失一般性，可设 x (t) ＞ 0 ， t ≥t0。由定理1的证明有

令t→∞，对上式取上极限，注意到条件(9)，有 ()wt→-∞，这与 () 0wt＞ 矛盾。所以方程(1)是振动的。定理2证毕。

推论1 若定理1中条件(8)改为

则方程（1）振动。

[1] 田学全,王洪珂,俞元洪.一类二阶半线性泛函微分方程的振动性[J].数学的实践与认识,2014,44(4):286-290.

[2] Xu R, Meng F. Some new oscillation criteria for second order quasi-linear neutral delay differential equations[J].Applied Mathematics and Computation, 2006, 182(1):797-803.

[3] Yang X. Oscillation criterion for a class of quasilinear differential equations[J]. Applied mathematics and computation, 2004, 153(1): 225-229.

[4] 林文贤.具非线性扩散系数的偶数阶中立型偏泛函微分方程的振动性[J].井冈山大学学报:自然科学版,2014,35(4):18-22.

[5] 林文贤,俞元洪.高阶中立型时滞微分方程的振动准则[J].应用数学学报,2014,37(6):1018-1024.