基于极限分析法的基坑支护入土深度研究

李和志，赵永清，陈春鸣

(1.江西科技学院南昌市材料研究与结构检测重点实验室，南昌 330098;2.湖南科技学院 土木工程与建设管理系，湖南永州 425199;3.东莞理工学院城市学院城市与环境科学系，广东东莞 523419)

1 研究背景

基坑工程周边环境和地质情况复杂性导致基坑安全事故频发，由此造成的人员伤亡和经济损失触目惊心，对基坑稳定性开展深入研究意义十分明显。目前，已有众多研究者对基坑稳定性进行了较为全面的研究，并取得一些研究成果［1－8］。基坑稳定性全面分析主要包括:整体稳定性分析、基坑坑底土体抗隆起稳定分析、支护桩抗倾覆稳定性分析、基坑渗流稳定性分析等。分析过程极其复杂，同时针对不同土质条件，基坑稳定性侧重有所不同。

近年来软土基坑支护工程实践表明，基坑底部土体抗隆起稳定性在基坑支护中往往起决定作用。进行抗隆起稳定性分析时，除对基坑底部土体处置外，通常还调整支护桩的入土深度，以达到基坑底部土体稳定目的，本文基于此，将通过极限分析上限法来确定软土基坑支护入土深度值。

2 软土基坑支护坑底速度场分析

软土基坑坑底土体在其一侧土体自重及外荷载作用下达到极限状态时，就会发生塑性流动，而它的流动方向迹线就是速度滑移线(见图1)。假定忽略AE面摩擦力，并假设滑移场土体为Coulomb材料且忽略其自重，基坑承受外荷载为q0，基抗开挖深度为H，土体为均质土且其重度为γ，黏聚力为c，内摩擦角为φ，基坑支护入土深度为t，则基坑支护桩底面以下的坑底土体主动区ABC所受的荷载值为q=q0+γ(t+H)，被动区 BDE所承受的荷载值为q1=γt。

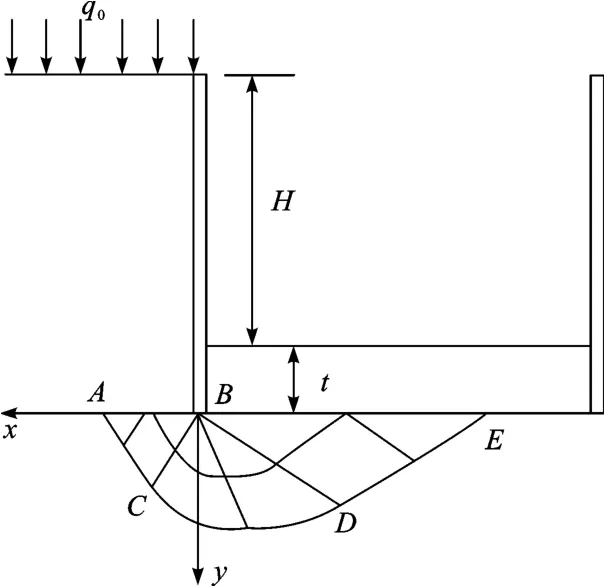
图1 基坑底部滑移线场Fig.1 Slip line field at the bottom of foundation pit

基于Hill机构建立如图2所示的基坑坑底塑性区的速度场。类似于文献［9］的Hill机构分析可知，该速度场由底角为主动滑移区ABC、中心角为的BCD对数螺旋过渡区及底角为的被动滑移区BDE构成。

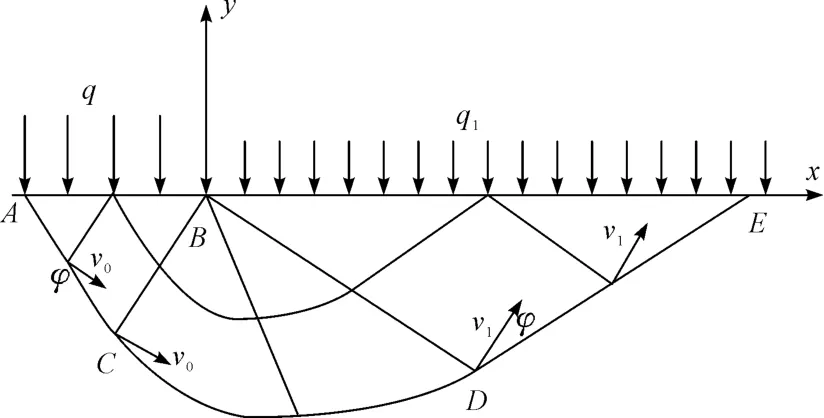
图2 基于Hill机构的速度场Fig.2 Velocity field based on Hill institution

因为塑性流动线ACDE以下的土体不受塑性变形影响，可视为静止状态，故此流动线为一条速度间断线。根据速度间断线特点可知，此线上的任何一点的速度方向与该点切线成φ角，即ACDEBA整个区域的ACDE边界上速度方向与该线成φ角，显然速度方向垂直塑性区一侧的α族滑移线，故而塑性区一侧的α族滑移线的速度 vα=0，又在ACDEBA整个区域中α族滑移线均为直线，则此整个区域内的速度vα均为0，同时在刚性区一侧的速度突变为0［9］。

2.1 主动滑移区ABC区域速度场分析

因AC边界上速度方向与该线成φ角，故而此区域在AB以上的压力q作用下产生以速度v0作垂直于BC面的塑性运动，假定支护桩底面以上的速度为v，则根据AB面的速度相容条件可得

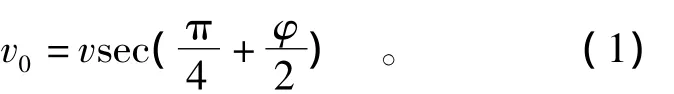
2.2 过渡区BCD区域速度场分析

在此区域中已知，vα=0，则根据沿β族滑移线速度场基本微分方程［10］有

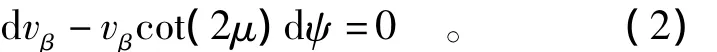
由上式积分得

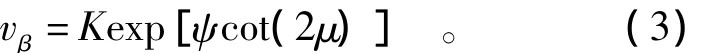
式中:μ为两滑移线的尖角;K为积分常数，根据边界条件求出。

不难分析，间断线BC右侧的速度及大小与其左侧完全一致，即

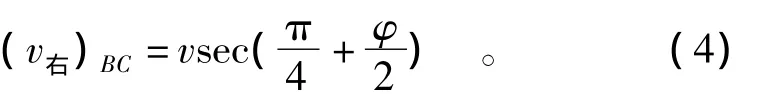
同时对数螺旋区边界BC右侧的vβ为

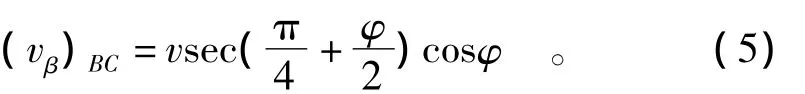
而边界 BC右侧的 vβ还可由式(3)表示，且 ψ=于是可求得积分常数K，即

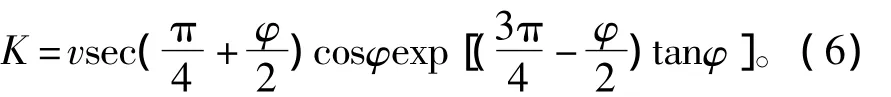
因而，对数螺旋过渡区BCD中沿α族、β族滑移线的速度分别为

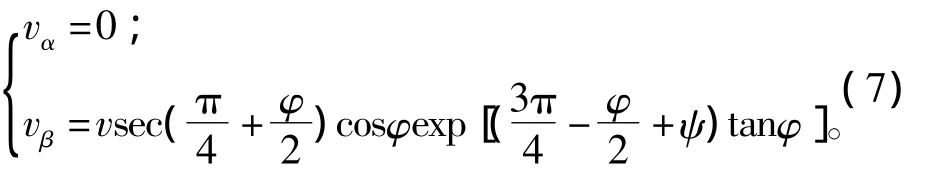
进而对数螺旋过渡区BCD中的速度为

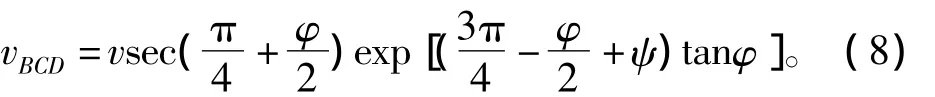
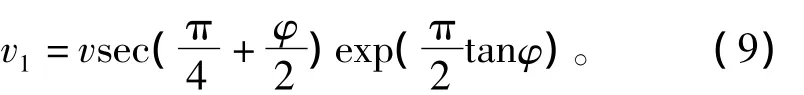
因而可知对数螺旋过渡区BCD的速度按指数规律由边线BC的(v右)BC逐渐变为BD的v1。

2.3 被动滑移区BDE区域速度场分析

因被动区BDE的边界BD的滑移速度方向与边界DE成φ角，不难证明边界BD的滑移速度方向与边界BD垂直，且其大小因在边界BD两侧的速度方向未发生改变而不变，即依旧为v1;并且此区域与主动区ABC有相似的特性，即都是均匀速度区，则被动区BDE可看成以速度v1垂直于BD面斜向上的刚体运动。

3 软土基坑支护入土深度上限解

经速度场分析可知:主动区ABC以速度v0与x轴正向成角作刚体运动;被动区BDE以速度v1与x轴正向夹角作刚体运动;对数螺旋过渡区BCD以速度vBCD绕B点按对数螺旋运动。ACDE间断面因其以下土体未发生运动，故而是一个速度间断面，BC，BD两面经上文分析可知并非跟Prandtl机构场一样，而是一个速度连续面。主动区ABC所受的荷载值为q，以速度v且方向垂直向下运动;被动区BDE所受的荷载值为q1，以速度方向垂直向上运动。

为研究基坑支护后坑底土体极限承载能力，先暂时假设速度间断面AB长为b，则根据图2及相关分析可得AC，BC的长度为

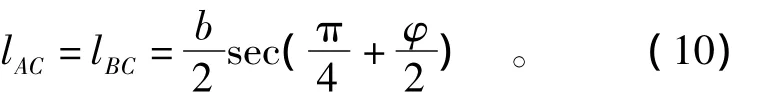
此外还可根据对数螺旋区BCD中的BC与BD的长度关系可推出:

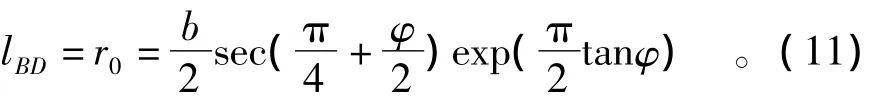
根据文献［11］可知:

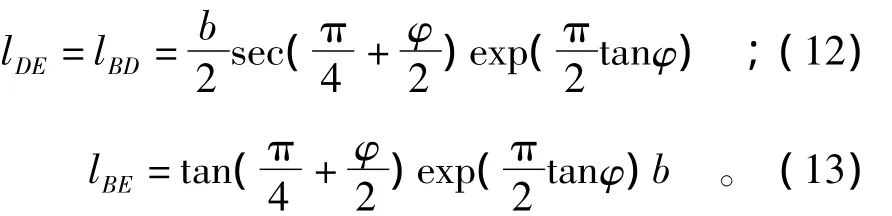
经上述分析可知，忽略滑动区内土体自重，则此机构场中q做正功，q1做负功，间断面 AC，CD，DE及对数螺旋区BCD均存有能量耗散。其中间断面AC，DE属于平移情况下的能量消散WAC，WDE，可分别通过式(14)、式(15)求出，即

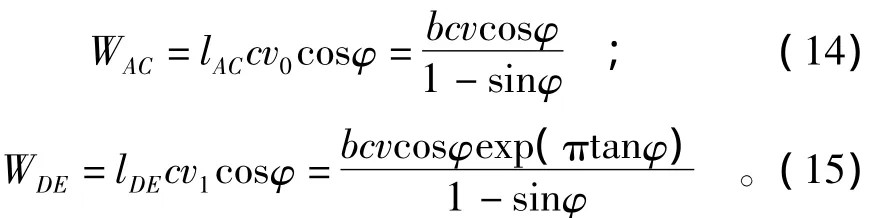
隔离过渡区BCD区域，并建立如图3所示的极坐标分析图，故而在计算间断面CD能量消散WCD时，还需要将其速度通过换元公式换成与矢径r相关的θ的参数，即假设ψ=θ－π，则式(8)可化为

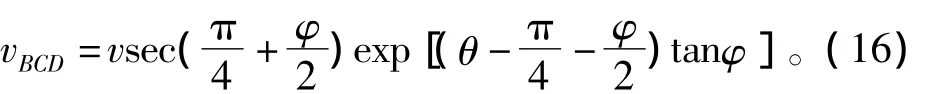
矢径r则为

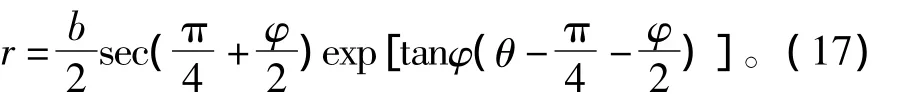
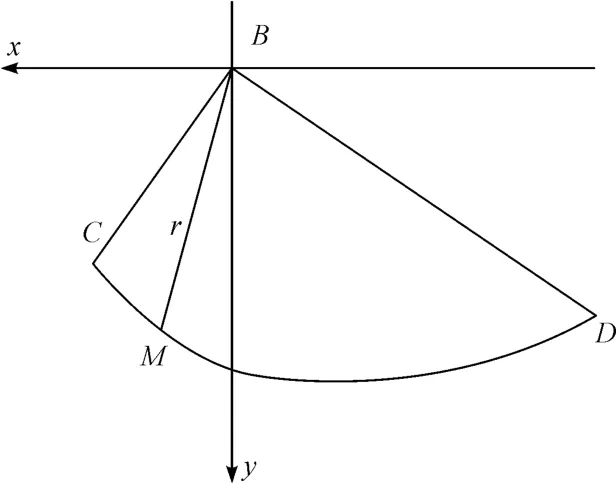
图3 BCD区域极坐标分析简图Fig.3 Polar coordinates in BCD region

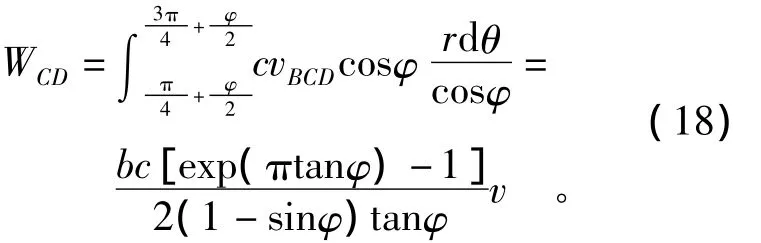
对数螺旋区BCD内的土体能量消散率WBCD可通过如图4所示的简图计算。

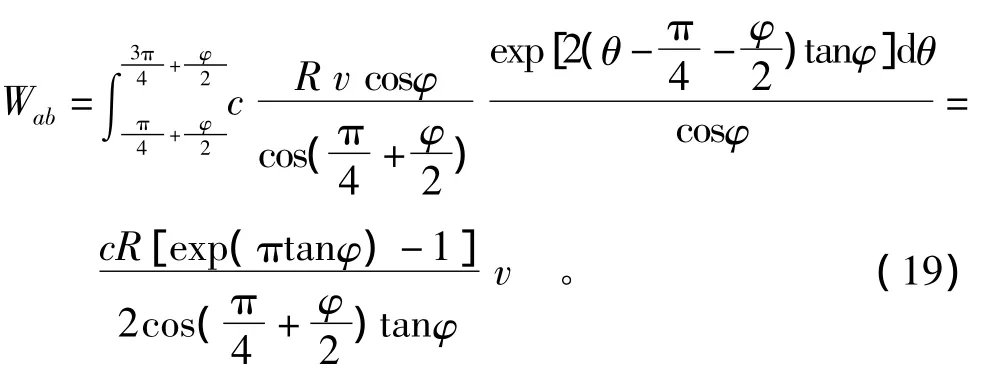
则微元aa'b'b能量消散率W可用式(20)计算，即

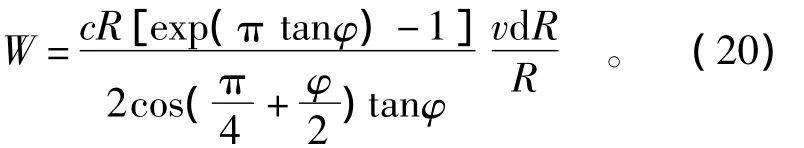
于是对数螺旋区BCD的能量消散率WBCD可通过对上式积分求得，即

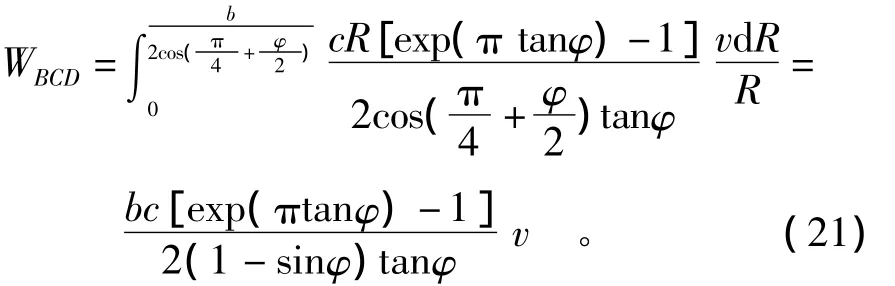
另一方面，外荷载q对此机构产生正功率Wq，即

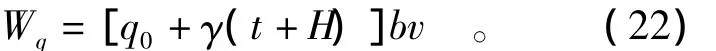
外荷载q1对此机构产生负功率Wq1，即

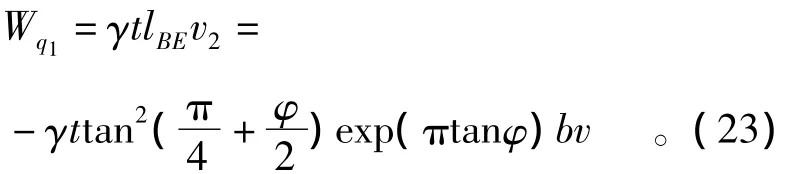
忽略此机构场土体的自重，再结合式(14)、式(15)、式(18)、式(21)至式(23)，可建立虚功率方程为

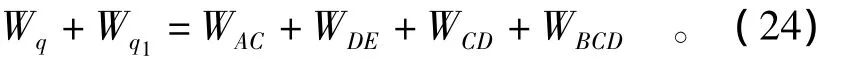
对此虚功率方程求解，便可求得基坑支护入土深度的上限解t和基坑底部极限荷载qf分别为

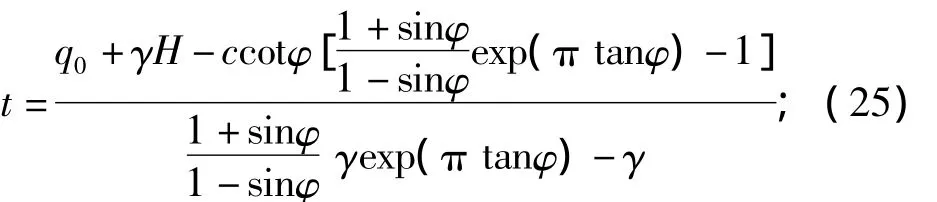
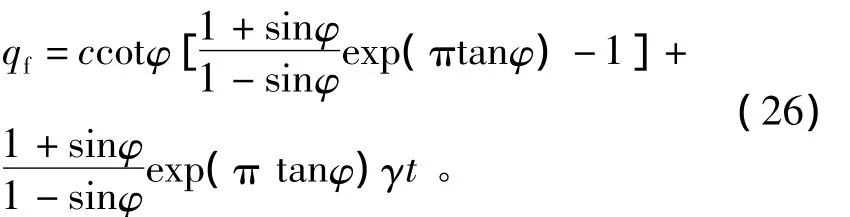
此外，假设实际支护入土深度为t，则基坑抗隆起稳定性安全系数为

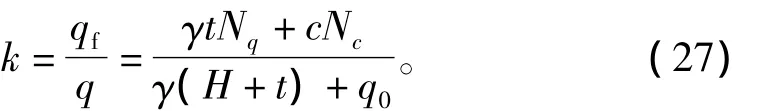
其中:

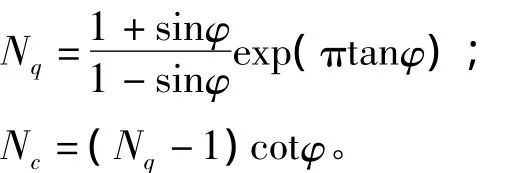
4 工程算例

采用文献［1］中的工程实例作为算例，该主楼基坑开挖深度H=11.65 m，支护桩桩长 l=24.55 m，超载q0=20 kPa。，基坑围护设计参数见表1。

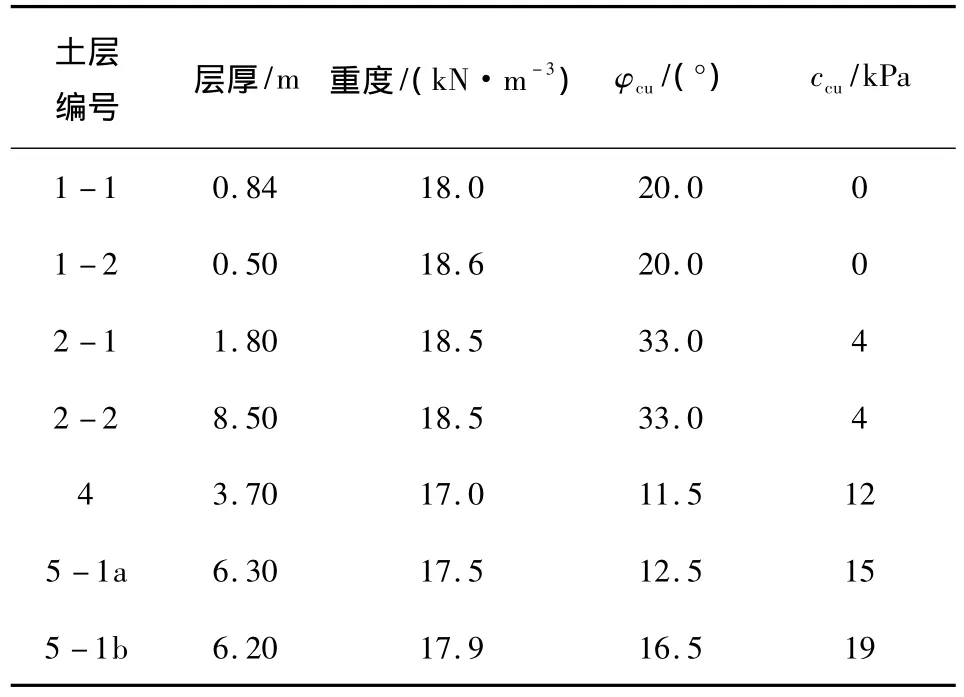
表1 基坑围护设计参数Table 1 Design parameters for braced excavations

根据式(25)和表1，并假设支护桩桩底在土层4内，可计算出该基坑的抗隆起稳定性理论支护入土深度上限解为4.05 m，超过3.7 m，但是考虑到5－1a土层的参数与土层4接近，且为安全考虑，该主楼支护桩入土深度上限解就是4.05 m。此外该基坑实际支护入土深度为12.9 m，且坑底土层参数取土层 4，5－1a，5－1b的厚度加权值，运用式(27)，可以求得该抗隆起稳定性安全系数k为1.94，且与文献［1］中的表2对比可知，本文稳定性分析是合理的，也从侧面上验证了本文基坑支护入土深度上限解。

5 结语

本文基于极限分析上限法分析了基坑底部的速度场，建立了相应的虚功率方程，推导出基坑抗隆起稳定安全性要求下的支护深度上限解和支护入土深度为t时的基坑抗隆起稳定性安全系数k的新的计算方法。

工程案例采用新计算方法求得其抗隆起稳定性安全系数k=1.94，与原结论对比吻合度非常高，验证表明本文稳定性分析是合理的，也从侧面验证了本文基坑支护入土深度上限解。该结论可为将来同类型的基坑支护入土深度计算提供参考和经验。

［1］秦会来，陈祖煜，刘立鹏.基于上限理论的软土基坑抗隆起稳定分析方法［J］.岩土工程学报，2012，34(9):1611－1619.(QIN Hui-lai，CHEN Zu-yu，LIU Li-peng.Basal Stability Analysis for Excavations in Soft Clay Based on Upper Bound Method［J］.Chinese Journal of Geotechnical Engineering，2012，34(9):1611－ 1619.(in Chinese))

［2］陈 刚，阮 澍，李九思.软土基坑喷锚支护设计与实例分析［J］.岩土力学，2002，23(增 1):161－164.(CHEN Gang，RUAN Shu，LI Jiu-si.Design and Analysis of Shotcreting and Anchoring Support Applied to Foundation Pit in Soft Soil［J］.Rock and Soil Mechanics，2002，23(Sup.1):161－164.(in Chinese))

［3］秦会来，黄茂松，王卫东.非均质软土基坑抗隆起稳定性的极限分析方法［J］.岩土力学，2008，29(10):2719－2724.(QIN Hui-lai，HUANG Mao-song，WANG Wei-dong.Limit Analysis Method for Basal Stability of Braced Excavation Against Upheaval in Heterogeneous Soft Clay［J］.Rock and Soil Mechanics，2008，29(10):2719－2724.(in Chinese))

［4］张耀东，龚晓南.软土基坑抗隆起稳定性计算的改进［J］.岩土工程学报，2006，28(增 1):1378－1382.(ZHANG Yao-dong，GONG Xiao-nan.Improvement on Basal Heave Stability Analysis for Excavations in Soft Clay［J］.Chinese Journal of Geotechnical Engineering，2006，28(Sup.1):1378－1382.(in Chinese))

［5］李镜培，唐 耀，张 飞.考虑支护结构的软土基坑抗隆起稳定上限分析［J］.地下空间与工程学报，2011，7(5):1007－ 1012.(LI Jing-pei，TANG Yao，ZHANG Fei.Analysis of Stability Against Upheaval of Excavation by Upper Bound Method Considering the Retaining［J］.Chinese Journal of Underground Space and Engineering，2011，7(5):1007－1012.(in Chinese))

［6］SHIRAW J，WEN D，NADARAJAH P，et al.Design Issues Related to Jet Grouted Piles at Base of Excavations［C］//Proceedings of Tunnels and Underground Structures.Singapore:A.A.Balkema，2000:639－645.(in Chinese))

［7］张玉成，杨光华，钟志辉，等.软土基坑设计若干关键问题探讨及基坑设计实例应用分析［J］.岩石力学与工程学报，2012，31(11):2334－2343.(ZHANG Yucheng，YANG Guang-hua，ZHONG Zhi-hui，et al.Discus-sion on Some Key Problems in Soft Soil Foundation Pit and Application Analysis of Design Example［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31(11):2334－2343.(in Chinese))

［8］刘 润，闫 玥，闫澍旺.支撑位置对基坑整体稳定性的影响［J］.岩石力学与工程学报，2006，25(1):174－178.(LIU Run，YAN Yue，YAN Shu-wang.Stability Analysis of Foundation Pit with Position Change of Braces［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(1):174－178.(in Chinese))

［9］陈惠发.极限分析与土体塑性［M］.詹世斌译.北京:人民交通出版社，1995.(CHEN Hui-fa.Limit Analysis and Soil Plasticity［M］.Translated by ZHAN Shi-bin.Beijing:China Communications Press，1995.(in Chinese))

［10］龚晓南.土塑性力学［M］.杭州:浙江大学出版社，1997:319－320.(GONG Xiao-nan.Soil Plasticity［M］.Hangzhou:Zhejiang University Press，1997:319－ 320.(in Chinese))

［11］赵永清.基坑支护结构土压力计算及坑底稳定性研究［D］.湘潭:湖南科技大学，2014:47.(ZHAO Yongqing.Calculation of Earth Pressure and Stability of Foundation Pit’s Retaining Structure［D］.Xiangtan:Hunan University of Science and Technology，2014:47.(in Chinese ))