单体滑坡灾害承灾体的有限元模拟与易损性评估

陈旭丹，孙新利，程金星，温伟伟

(1.第二炮兵工程大学 一系，西安 710025;2.第二炮兵装备研究院，北京 100085)

滑坡是一种常见的地质灾害，具有突发性、瞬时性和不易监测性等特点，对生命财产，特别是桥梁、建筑、公路等基础设施都具有巨大的破坏能力。

滑坡灾害风险评估是国内外倡导和推广的减灾防灾有效途径［1］。比较主流的滑坡灾害风险R的表达式为

式中:H为滑坡危险性;V为承灾体易损性;E为承灾体价值。目前关于滑坡灾害方面的研究还主要集中在潜在滑坡本身的监测预警方面，对滑坡灾害风险评估尚处于从定性评估到半定量计算的发展阶段［2］。此外，当前的评估模型通常针对一定区域内滑坡灾害，对生命财产采用定性的指标进行评估，但对单体滑坡灾害风险评估的研究尚少。其中，承灾体易损性V是滑坡灾害风险评估的重点，评估方法选择合理与否是制约评估发展的瓶颈。本文采用有限元分析软件SAP2000对单体滑坡灾害中承灾体形变过程进行模拟，并对承灾体易损性计算方法进行初步探讨。

1 易损性基本概念与分析

滑坡灾害易损性定义为:“在一定灾害强度下承灾体损失程度，是0～1之间的系数”［3］。可知，滑坡灾害易损性主要和滑坡致灾强度与承灾体抗灾能力有关，其关系可以表达为

式中:I为滑坡致灾强度;C为承灾体抗灾能力。

根据定义可知:

(1)滑坡致灾强度强调了致灾能量来源，与滑坡基本条件和能量转化过程有关。

(2)承灾体抗灾能力反映了承灾体抵抗滑坡灾害和恢复的能力，与承灾体结构有关。

(3)当滑坡致灾强度小于承灾体抗灾能力时，V介于0和1之间;当滑坡致灾强度超过承灾体抗灾能力时，V为1。

2 易损性评估模型

2.1 滑坡体运动过程与分析

滑坡失稳后滑坡体的运动过程可等效为重力势能转化为冲击能这一物理过程，能量转化过程如图1。

滑坡体运动是一个复杂的非线性过程，其能量转化、消耗不仅与滑动路径有关，也与承灾体结构有关，简化模型如图2。滑坡失稳后重心下降，重力势能向冲击能转化，滑坡体做加速度先增大后减小的加速运动［4］，此时一部分动能由于坡面和水平面摩擦而转化为内能。滑坡冲击体到达承灾体承载面时以冲击能形式破坏承灾体，承灾体表面发生弹塑性变形和整体侧向偏移，当冲击体的冲击力超过承灾体的屈服极限时，承灾体将倒塌失效。

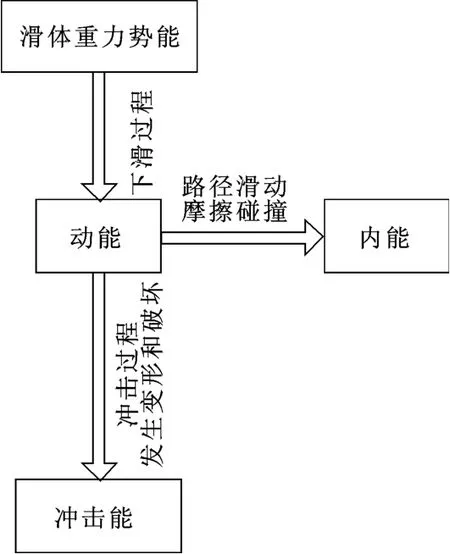
图1 滑坡体运动能量转化过程Fig.1 Energy conversion process of landslide body movement

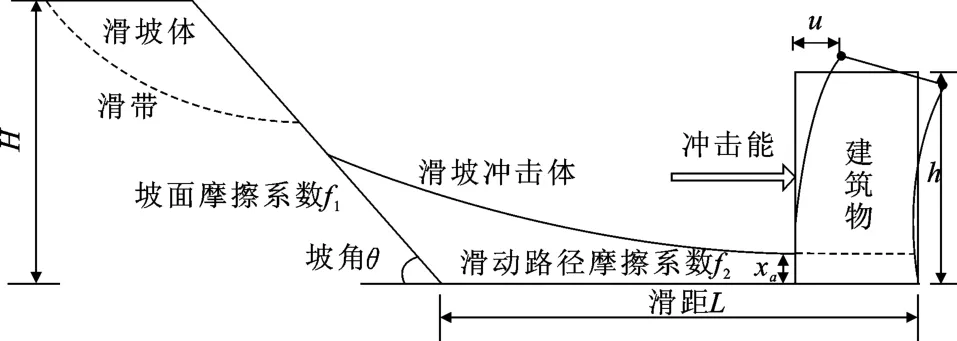
图2 滑坡体运动简化模型图Fig.2 Simplified model of landslide body movement

2.2 承灾体破坏过程

根据滑坡体与承灾体的位置关系，滑坡对承灾体的影响可以分为2种情况:①承灾体位于滑坡体上时，一旦滑坡失稳，承灾体失效概率为1;②承灾体不在滑坡体上但位于冲击体影响范围之内，此时承灾体易损性与承灾体相对位置及抗灾能力有关。故本文主要考虑第2种情况，并假定承灾体为典型的钢筋混凝土框架结构。

文献［5－7］在研究承灾体易损性时，往往将承灾体构件看成弹性结构，以材料超过其容许应力作为失效标准，即一旦构件进入塑性阶段即失效。实际中，钢筋混凝土梁(或柱)纵筋屈服后，截面可以有较大转角，形成类似于铰一样的效果［8］。在载荷作用下，塑性铰截面不能承担的过剩载荷通过变形协调的原则传给其余结构部分，内力重新分配后会达到新的平衡。如果在结构设计中考虑塑性铰，那么此结构一定是超静定的。这样框架结构变形将分为弹性变形和塑性变形，更符合实际变形过程。

对于典型塑性铰，可以用一条曲线来表征广义力－位移关系，如图3所示:点A是原点;点B代表屈服点，在到达点B前，塑性铰尚未形成，无塑性变形;点C代表极限承载力点;点D代表残余强度点;点E代表完全失效点。其中，IO对应立即使用点，LS对应生命安全点，CP对应防止坍塌点。结构整体所受侧向力与监测位移之间的关系与该曲线类似，即建筑物在受到侧向力时，整体首先发生弹性弯曲，当侧向力达到一定程度时发生塑性变形，进一步超过极限基底剪力时，建筑物将发生坍塌，如图4，L1为原点，L2为基本完好控制点，L3为威胁生命控制点，L4为结构失稳点，L5为完全失效点。根据塑性铰状态和结构破坏程度，参考刘晶波等［9］、吴越等［10］和《GB/T 24335－2009建(构)筑物地震破坏等级划分》标准［11］，可以认为在侧向力－位移曲线中也基本符合塑性铰中广义力－位移关系对应的破坏等级标准，如表1所示。

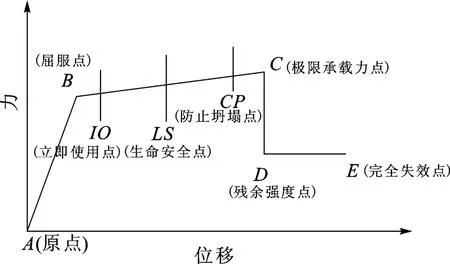
图3 塑性铰广义力-位移曲线Fig.3 Curve of generalized force vs.displacement of plastic hinge

表1 建(构)筑物破坏等级标准Table 1 Standards of damage classification

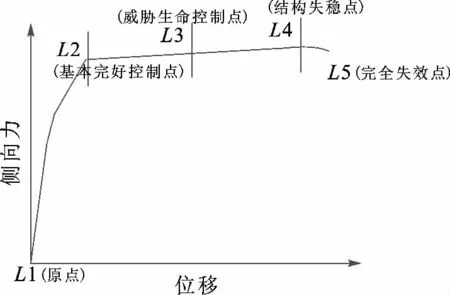
图4 塑性铰侧向力-位移曲线Fig.4 Curve of side force vs.displacement of plastic hinge

2.3 简化模型

在讨论滑坡运动过程和承灾体破坏过程的基础上，引入结构塑性变形过程，对何思明等［12－13］泥石流大石块冲击力简化计算方法进行改进，构建滑体冲击模型。

如图2，滑坡对建筑物的最后冲击能为

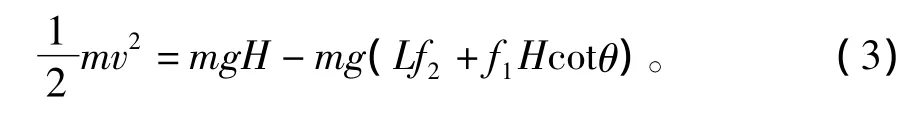
式中:v为冲击体接触到建筑物表面时速度;H为滑坡体重心落差;θ为坡度;L为建筑物距坡脚距离;f1为坡面摩擦系数;f2为滑动路径摩擦系数;m为冲击体质量，估算m=d2Aρ，d为冲击体厚度，A为受冲击面宽度，ρ为滑土体密度。其中坡面摩擦系数f1可以根据谢得格尔法［14－15］，即通过滑坡体积确定f1:

式中:a=－0.156 66;b=0.622 19。上式适用于一般滑坡;摩擦系数也可采用工程地质类比法，通过对典型滑坡的反演分析确定［16］。

类比泥石流大石块对钢筋混凝土结构的冲击问题，将建筑物简化为悬臂梁结构。则冲击体对建筑物的冲击作用简化为竖向悬臂梁受到水平载荷作用。弯曲变形能表达式为

式中:P为水平载荷;x0为载荷作用的位置，这里可以认为是d;EI为抗冲击刚度。其中抗冲击刚度可以用建筑物整体侧向刚度计算:

式中:q为侧向倒三角形分布载荷中最大分布载荷;h为建筑物高度;u为倒三角分布载荷作用下结构顶点质心的弹性水平位移。

建筑物在整体发生弯曲变形的同时，表面发生的弹塑性变形吸收了一部分冲击能。表达式为［17］

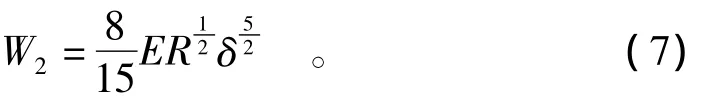
式中:E为等效弹性模量;δ为表面法向压缩量;R为等效半径。接触面的压力P与法向变形之间有如下关系:

将式(8)代入式(7)可简化为

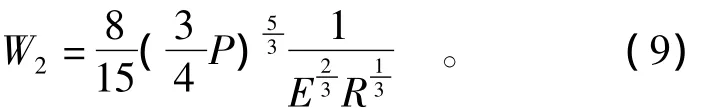
建筑物总变形能为

由于在泥石流冲击防撞墩的模型中等效半径R为大石块半径R1，对于冲击体，前端面曲率半径趋近0，则等效半径趋于无穷大值，式(9)中等效弹性模量E数量级为1010，故W2趋近于0。实际中，侧向力作用的时间很短，在滑坡冲击体的尺度下建筑物表面变形能与建筑物整体弯曲变形能相比很小，可以忽略不计，故W=W1。

假设滑坡冲击结束后速度与建筑物速度都为0，冲击能完全被建筑物吸收形成破坏能，则功能关系为

将式(3)和式(5)代入式(11)可得P与L的函数关系，即

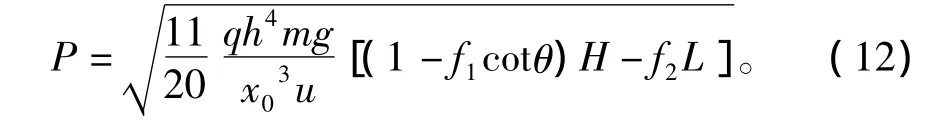
建筑物在受到冲击体冲击时存在极限载荷Pm，当P超过Pm时，建筑物底层塑性铰处于C状态以上，也就是基底剪力到达极限承载能力，建筑物将发生倒塌。所以用Pm代表易损性V函数关系中C，用P代表I，则易损性可以表示为

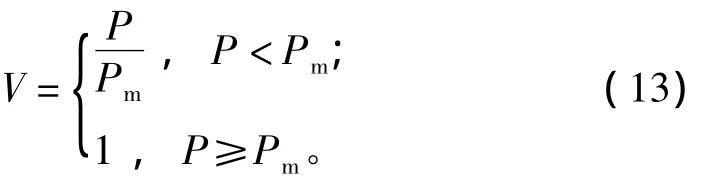
参考表1建(构)筑物破坏等级标准，结合建筑物受侧向力作用直至倒塌位移曲线，给出表2结构破坏等级标准与易损性量化指标关系。当易损性取不同值时可以确定承灾体破坏等级。

表2 结构破坏等级标准与易损性量化指标关系Table 2 Relationship between damage classification standard of structure and quantitative index of vulnerability

3 算例分析

采用上述易损性模型对一典型滑坡影响下钢筋混凝土框架结构进行易损性分析。有限元模型如图5，承灾体是3层钢筋混凝土框架结构，x向跨数3，跨宽6m，y向跨数2，跨宽6 m，层高4m，混凝土强度采用C30，楼面为120 mm混凝土板，梁截面为矩形457 mm×254 mm，柱截面为矩形600 mm×600 mm，配筋采用Q235，h=12m，示意图如图5。其中，柱的塑性铰采用SAP2000中P－M2－M3耦合类型(配筋3×3)，梁采用 M3耦合类型。参考俄村右岸滑坡［18］，滑坡体重心落差 H=90 m，坡度 θ=40°，坡面摩擦系数f1=0.40(当滑坡体积 V0=2.89×106m3时可采用式(4)得出)，滑动路径摩擦系数f2取0.5，密度 ρ=1.9×103kg/m3，冲击体厚度 d=5 m，A=12 m，m=52×12 ×1 900=5.7 ×105kg。

图5 有限元模型Fig.5 Finite element model

3.1 计算过程

(1)侧向刚度求解。采用软件SAP2000中的“位移控制”对所建立的钢筋混凝土框架结构进行侧向倒三角分布载荷分析。可知当侧向倒三角形分布载荷最大q=180 kN/m时，位移为0.21 m，如图6所示。根据式(6)可求得建筑物整体侧向刚度EJd=1.63 ×103kN/m2。

(2)变形过程模拟。对建筑物x0=5 m处分步施加水平载荷P直至建筑物倒塌，记录水平载荷P、基底Fx向剪力与顶点水平位移，见表3。水平载荷与顶点水平位移曲线如图7。模拟建筑物倒塌失效时塑性铰分布如图5。

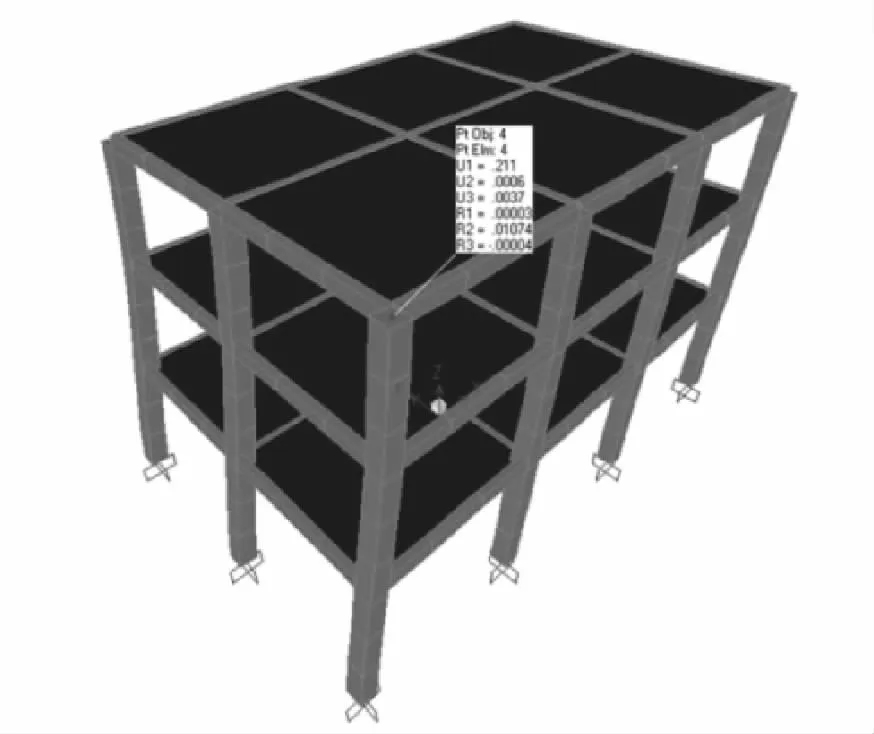
图6 力控制结果Fig.6 Result of force control

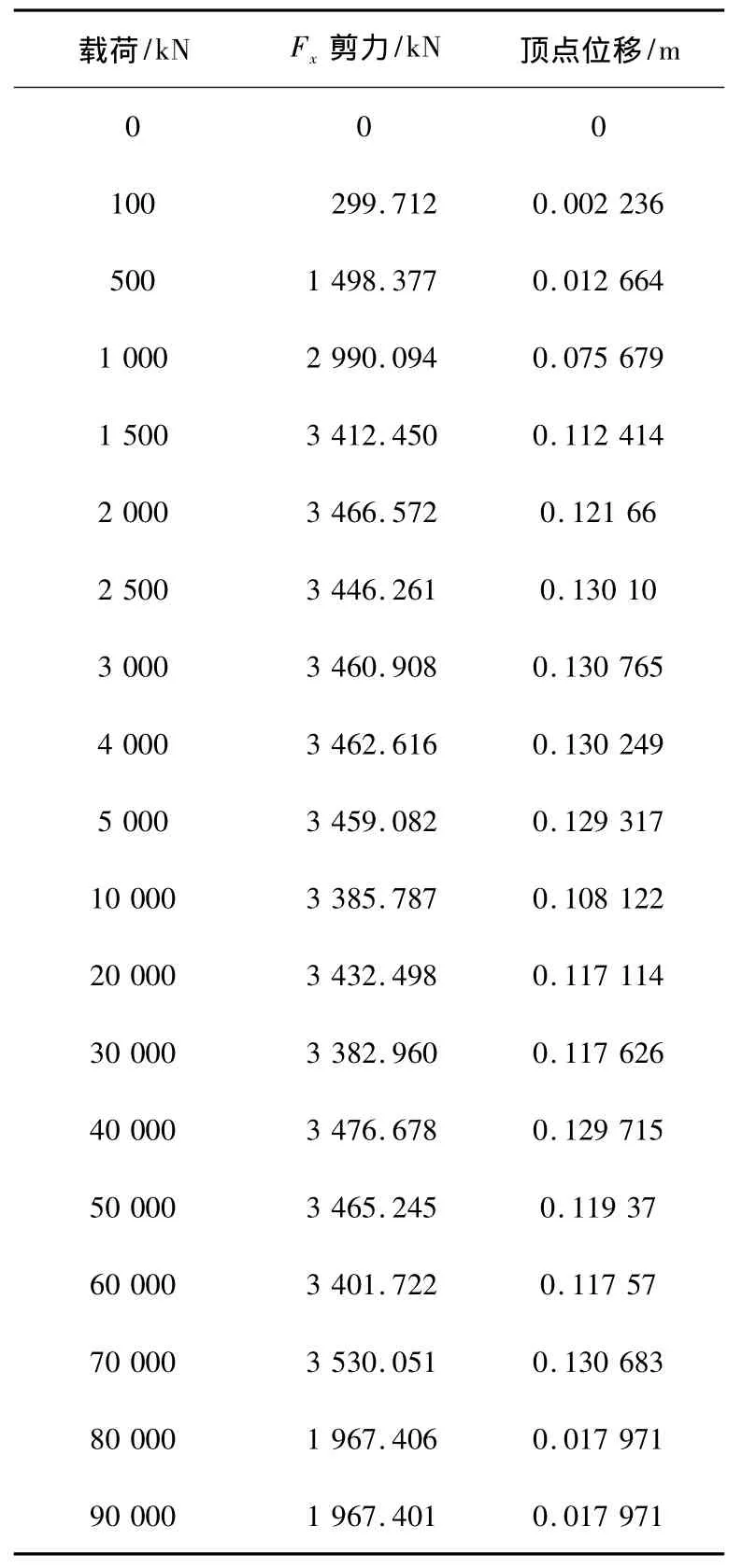
表3 建筑物变形过程模拟结果Table 3 Simulated results of building's deformation

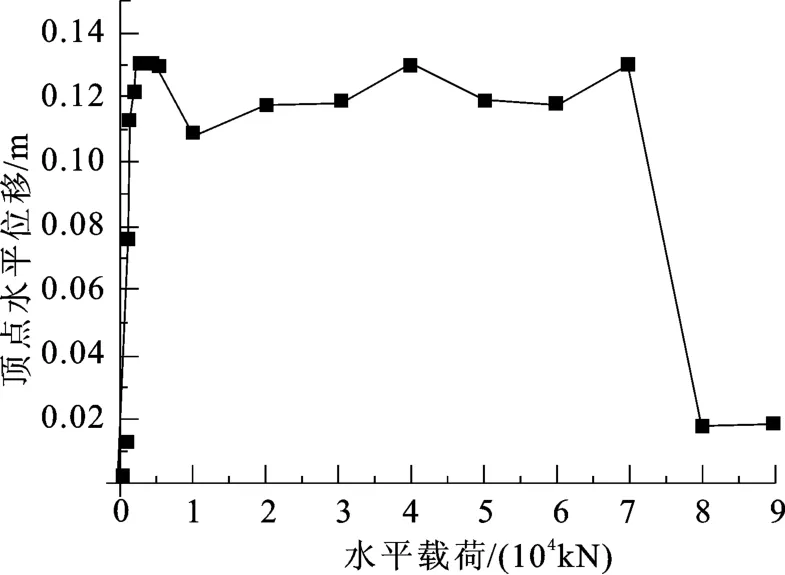
图7 水平载荷与顶点水平位移曲线Fig.7 Curve of horizontal load vs.horizontal displacement

结合表3和图7，可认为Pm为70 000 kN。从图5中可以看出基底最先出现塑性铰且最先到达C状态。通过观察塑性铰所处阶段和顶点水平位移变化，可以确定不同P值所对应弹塑性变化阶段。

(3)易损性求解。根据式(3)，令v=0，求出冲击体最大位移Y，则Y=92.7 m，接近俄村右岸滑坡实际滑距，即安全距离。然后将上述建立的典型滑坡和建筑物参数代入式(12)得出P和L的函数关系，如图8。

假设建筑物距坡脚的距离L=85 m，由式(12)可得 P=4.095 7×104kN，代入式(13)得 V=0.585，参照表2可知建筑物发生中等破坏。

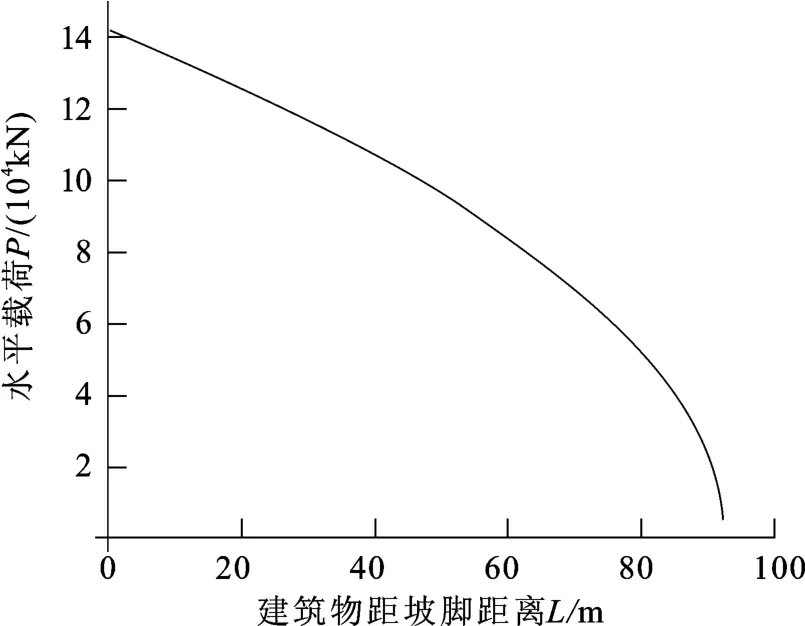
图8 P-L曲线Fig.8 P-L curve

3.2 结果分析

(1)由表3和图7可以看出，建筑物在受力时整体发生偏移，侧向力与顶点水平位移关系和塑性铰广义力－位移关系相近，可以说这是局部塑性铰变形在建筑物整体变形中的反映。此外，建筑物最先发生弹性变形，但是完全弹性变形阶段所占比重很小，建筑物在受到巨大外力作用时往往处于塑性变形阶段，由于塑性铰的作用，抗力不断增加。

(2)从模型求解的结果来看，建筑物距离坡脚越远，P-L曲线斜率的绝对值越大。这说明建筑物距坡脚距离L越大，P减小越快，易损性V也减小越快，建筑物越安全。同样，令P=Pm，即V=1时，不难得出L=69.6 m，可知在该滑坡下，建筑物的L＜69.6 m必然倒塌。

4 误差讨论

本文所采用的模型较为简化，然而滑坡是一个复杂的非线性系统，承灾体也经历了复杂的非线性变化，所以本文得出的结果只能作为划分承灾体易损性的参考。模型误差主要来源有:

(1)滑坡运动内部能耗［19］。滑坡运动内部能耗主要指2个阶段，一是滑坡在下滑运动至接触承灾体之前的内部能耗，这部分能耗与滑体内部作用机制有关;二是冲击体破坏承灾体的过程中内耗，这部分内耗与冲击体内部作用和承灾体形变过程有关。这2个过程都消耗了部分向动能转化的重力势能。实际上，滑坡运动问题为典型的不连续变形块体的动力学问题，采用离散元法能够分析滑坡运动过程中的内耗。

(2)滑动摩擦能耗。本文在滑坡多运动过程中分别采用了坡面摩擦系数f1和滑动路径摩擦系数f2，前者采用了经验法谢得格尔法得到，具有经验性质;后者则因滑坡体转化为冲击体后内部结构的改变和摩擦路径颗粒等条件不断变化，很难真正获得实际的摩擦系数，只能采用经验的数值。对于具体滑坡的摩擦系数还有待于进一步研究。

5 结语

本文从滑坡灾害风险评估概念出发，主要对概念中承灾体的易损性V进行讨论，引入了承灾体结构表面和整体的弹塑性变形过程，对当前主流方法进行了改进，给出了针对单体滑坡灾害中承灾体易损性评价的简单方法。同时应用有限元软件对典型钢筋混凝土框架结构进行数值模拟，并将承灾体整体破坏等级与塑性铰的破坏等级做比较，给出了承灾体易损性量化值，有助于承灾体结构破坏等级划分。此外，本文中滑坡运动内部能耗和摩擦系数的改变并未考虑进去，有待进一步研究。

［1］FELL R，LACASSE S，LEROI E.A Framework for Landslide Risk Assessment and Management［C］//Proceedings of the International Conference on Landslide Risk Management.Vancouver，Canada:A.A.Balkema，May 31-June 3，2005:3－26.

［2］吴 越，刘东升，陆 新，等.承灾体易损性评估模型与滑坡灾害风险度指标［J］.岩土力学，2011，32(8):2487－2499.(WU Yue，LIU Dong-sheng，LU Xin，et al.Vulnerability Assessment Model for Hazard Bearing Body and Landslide Risk Index［J］.Rock and Soil Mechanics，2011，32(8):2487－2499.(in Chinese))

［3］Australia Geomechanics Society.A National Landslide Risk Management Framework for Australia［J］.Australia Geomechanics，2007，42(1):1－12.

［4］秦 云，姜清辉，郭慧黎.滑坡速度预测的计算方法探讨［J］.岩土力学，2008，29(增):373－378.(QIN Yun，JIANG Qing-hui，GUO Hui-li.Discussion on Two Methods for Predicting Velocity of Landslides［J］.Rock and Soil Mechanics，2008，29(Sup):373－378.(in Chinese))

［5］薛 强，张茂省，孙萍萍，等.基于多期DEM和滑坡强度的滑坡风险评估［J］.地质通报，2013，32(6):925－ 934.(XUE Qiang，ZHANG Mao-sheng，SUN Ping-ping，et al.Landslide Risk Assessment Based on Multi-period DEM and Activity Intensity［J］.Geological Bulletin of China，2013，32(6):925－934.(in Chinese))

［6］胡瑞林，范林峰，王珊珊，等.滑坡风险评价的理论与方法研究［J］.工程地质学报，2013，21(1):76－84.(HU Rui-lin，FAN Lin-feng，WANG Shan-shan，et al.Theory and Method for Landslide Risk Assessment:Current Status and Future Development［J］.Journal of Engineering Geology，2013，21(1):76－84.(in Chinese))

［7］李红英，谭跃虎，李二兵.库区单体滑坡灾害风险定量评估研究［J］.地下空间与工程学报，2013，9(增2):2040－2046.(LI Hong-ying，TAN Yue-hu，LI Er-bing.Research on Quantitative of Landslide Assessment Disaster Risk in Reservoir Area of Kala Hydropower Station［J］.Chinese Journal of Underground Space and Engineering，2013，9(Sup.2):2040－2046.(in Chinese))

［8］闫 冬，戚春香，冯清海，等.SAP2000结构工程分析及实例详解［M］.北京:中国建筑工业出版社，2009:216－223.(YAN Dong，QI Chun-xiang，FENG Qinghai，et al. Engineering Structure Analysis by Using SAP2000 and Examples［M］.Beijing:China Building Industry Press，2009:216－223.(in Chinese))

［9］刘晶波，刘阳冰，闫秋实，等.基于性能的方钢管混凝土框架结构地震易损性分析［J］.土木工程学报，2010 ，43(2):39－47.(LIU Jing-bo，LIU Yang-bing，YAN Qiu-shi，et al.Performance-based Seismic Fragility Analysis of CFST Frame Structures［J］.China Civil Engineering Journal，2010，43(2):39－47.(in Chinese))

［10］吴 越，刘东升，陆 新，等.基于功能关系的滑坡典型受灾体易损性评估模型［J］.岩石力学与工程学报，2011，30(增 1):2946－ 2953.(WU Yue，LIU Dong-sheng，LU Xin，et al.A Quantitative Vulnerability Assessment Model for Typical Element at Landslide Risk Based on Work-energy Transformation［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(Sup.1):2946－2953.(in Chinese))

［11］GB/T 24335－2009，建(构)筑物地震破坏等级划分［S］.北京:中国标准出版社，2009.(GB/T 24335－2009，Code for Classification of Earthquake Damage to Buildings and Special Structures［S］.Beijing:Standards Press of China，2009.(in Chinese))

［12］何思明，李新坡，吴 永.考虑弹塑性变形的泥石流大块石冲击力计算［J］.岩石力学与工程学报，2007，26(8):1664－ 1669.(HE Si-ming，LI Xin-po，WU Yong.Calculation of Impact Force of Outrunner Blocks in Debris Flow Considering Elastoplastic Deformation［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(8):1664－1669.(in Chinese))

［13］何思明，吴 永，沈 均.泥石流大块石冲击力的简化计算［J］.自然灾害学报，2009，18(5):51－56.(HE Si-ming，WU Yong，SHEN Jun.Simplified Calcul-ation of Impact Force of Massive Stone in Debris flow［J］.Journal of Natural Disasters，2009，18(5):51－ 56.(in Chinese))

［14］陈丽霞，殷坤龙，汪 洋.单体滑坡灾害风险预测［J］.自然灾害学报，2008，17(2):65－70.(CHEN Li-xia，YIN Kun-long，WANG Yang.Discussion on Risk Prediction for Single Landslide［J］.Journal of Natural Disasters，2008，17(2):65－70.(in Chinese))

［15］刘朋辉.滑坡滑动机理及风险评价研究［D］.北京:北京工业大学，2007.(LIU Peng-hui.Landslide Mechanism and Risk Evaluation［D］.Beijing:Beijing University of Technology，2007.(in Chinese))

［16］潘家铮.建筑物的抗滑稳定和滑坡分析［M］.北京:水利出版社，1980:120－122.(PAN Jia-zheng.Stability Analysis of Structure and Landslide［M］.Beijing:China Water Conservancy and Hydropower Press，1980:120－122.(in Chinese))

［17］王 强，何思明，张俊云.泥石流防撞墩冲击力理论计算方法［J］.防震减灾工程学报，2009，29(4):423－427.(WANG Qiang，HE Si-ming，ZHANG Jun-yun.Theoretical Method for Calculating Impact Force on Debris Flow Protection Piers［J］.Journal of Disaster Prevention and Mitigation Engineering，2009，29(4):423－427.(in Chinese))

［18］李军霞.西藏隆子县滑坡灾害形成机理及非线性预测研究［D］.长春:吉林大学，2011.(LI Jun-xia.Formation Mechanism and Non-linear Prediction of Landslide Hazards in Longzi County，Tibet［D］.Changchun:Jilin University，2011.(in Chinese))

［19］郑书彦，李占斌，李甲平，等.滑坡侵蚀离散元分析研究［J］.岩石力学与工程学报，2005，24(12):2124－2128.(ZHENG Shu-yan，LI Zhan-bin，LI Jia-ping，et al.Study on Landslide Erosion by Discrete Element Method［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(12):2124－2128.(in Chinese ))