动态模糊神经网络在船舶航向控制器上的应用

周剑敏

(浙江国际海运职业技术学院，浙江 舟山316021)

1 船舶航向控制

当船舶在狭窄海域中航行时，极易发生碰撞事故，因而船舶的航向控制问题，一直是研究的热点之一。在船舶行驶过程中，由于海岸的作用，船体常常会因为海浪的不规则扰动，而产生不对称力，尤其在狭窄海域中，这种不对称力被进一步放大，从而使得对船舶进行精细的控制变得十分困难［1］。通常情况下，只有经验丰富的海员，才能解决问题。为了解决这一过程对于人工和专家知识的依赖，需要一种自动化的控制器，一些学者提出了船舶模型控制方法，将船舶控制的各种因素建模，然后利用相应的模糊规则来调整船舶的航向和姿态。由于船舶在航行中受到不断的微小扰动，因而难以分辨船舶航行的变化究竟是海面的作用还是自动控制器的调整行为，使得该方法的实用性受到了限制。

为了能够设计一种自动化的自动模糊控制器，部分学者提出了一种基于模糊神经网络的方法［2-5］，利用遗传算法对控制器中的相关参数进行训练。然而，这种方法的缺点是训练的过程太长，可实现性较低。

此外，基于间接自适应模糊控制的方法也被应用于航向控制器中，但是在这种方法中自适应模糊控制规则的产生非常困难，因而在实用过程中，对于专家知识的依赖仍然比较严重。

为了解决以上问题，有学者提出了一种将模糊控制器与多结构控制方法相结合的方案。这种方案继承了多结构控制器的可靠性，同时利用模糊控制器来确定多结构控制器中的重要参数，能够在系统较为可靠的基础上，实现较好的灵活性和精确性。这种方案的缺点在于多结构控制器的设计和实现比较复杂，应用其中的模糊规则较难设计，制约了该方法的实用性。

基于对以上研究成果的研究和分析，本文提出了一种将船舶控制模型与模糊控制机制相混合的方法。使用船舶控制模型，保证了该方法的可靠性，同时降低了方法的实现难度。为了实现较好的灵活性，本文设计了一种动态神经网络，用来确定船舶模型控制过程中的3个重要参数。最后，本文对提出的方法进行了实验验证，证明了该方法具有较好的可靠性和灵活性。

2 船舶模型控制器

2.1 海面动态模型

对船舶航向和航行姿态的控制，通常通过调整推进器、船舵、首尾舵面等方法。因而船舶的动态模型是一个六自由度过程(DOF)。在该DOF 中，有3个水平运动和3个滚动运动，通常情况下，这些运动非线性、随机且紧密结合。在实际应用中，通常认为对于船舶的航向和姿态控制，关键在于航向的控制，而其他姿态的运动，由于幅度较小，因而可以忽略。在这种前提下，在横轴上，可以将运动模型抽象为:

其中:g(x)为船舶的航向;T和K 分别与船舶的速度和载重相关，并随着环境的变化而变化，所以航向控制器需要不断调整以适应T和K的变化。根据式(1)中表示的转移函数，可将运动模型的状态空间表示如下:

2.2 模型控制器设计

令g*(x)为预定航向，e=g(x)- g*(x)为预定航向与当前航线之间的误差，则可得船舶模型的状态空间为:

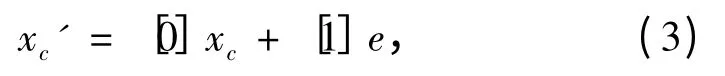
其中xc为模型的状态变量。除了xc外，船舶模型的基本变量还有g(x)和g′(x)，则状态反馈矩阵为:

其中Kc为模型的增益。根据以上方程，可得模型控制器的基本结构如图1所示。同时可将图1 中的带有反馈的控制器表示为:

由于g(t)=g*(t)-e(t)，且g′(t)=-e′(t)，则式(5)可以表示为

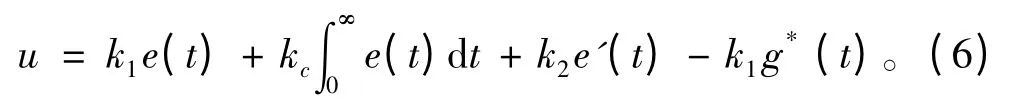
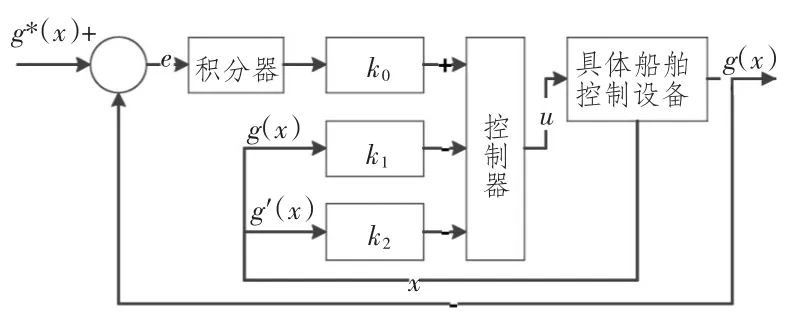
图1 船舶航向控制器结构图Fig.1 Structure of ship course controller

根据式(6)可知，前3 项为PID控制系统，最后一项k1g*(t)使得船舶控制系统成为一个状态反馈系统，同时闭环系统的极点决定了系统控制行为的性能。

将闭环系统看做一个串联系统，则可得串联系统矩阵为:

若令a=K/T，b=1/T，则矩阵可简化为:

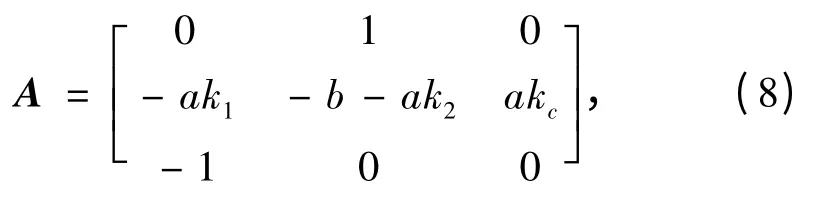
则该串联系统的特征多项式为:

令λ1，λ2，λ3为闭环系统的极点，则航向闭环控制系统的特征多项式为:

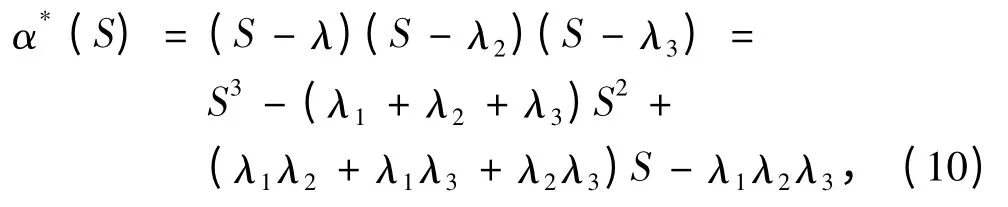
则可得控制器参数与极点的关系为:

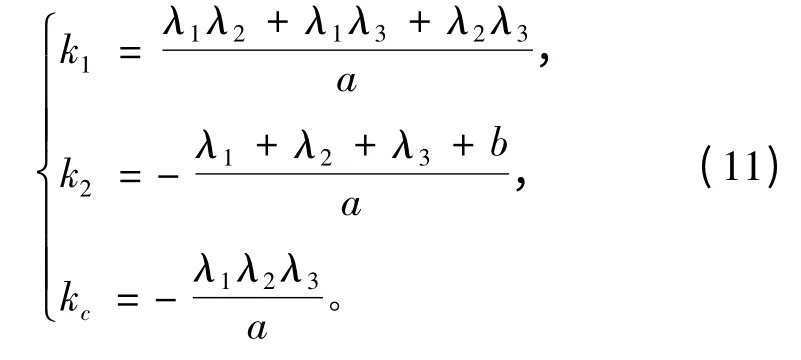
其中λ1、λ2为主要极点，需要利用训练和学习过程得到，令λ′1、λ′2为最优极点，则:

其中σ 为比例系数，则在不同的比例系数下，航向控制器的性能表现如图2所示。

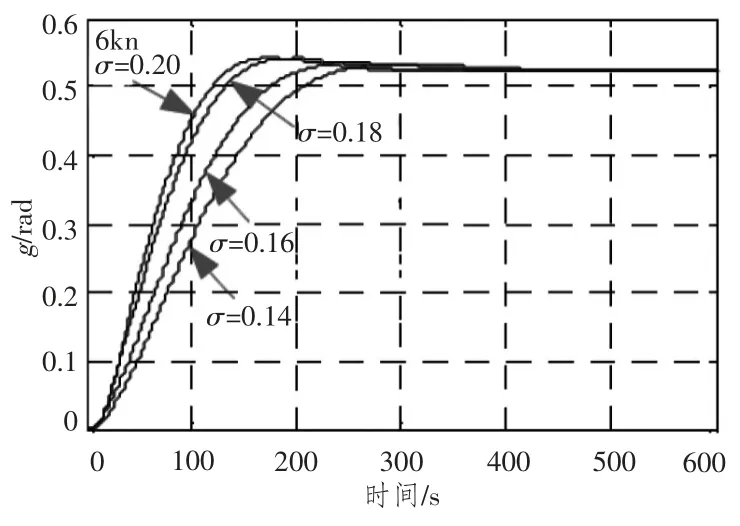
图2 不同比例系数性能图Fig.2 Performance under different σ

由图2 可知，当σ 越大时控制系统的灵活性就越高，然而其控制的幅度也会变大，造成较大的误差。为了保证系统的灵活性和精确性，需要对σ 进行确定，本文设计了一种模糊神经网络来解决该问题。

3 动态模糊神经网络

船舶的运动主要由误差e(t)和航向变动率g′(t)来确定。富有经验的船员在操作船舶时，当误差逐渐变大时，会通过适当增大舵面角度来调整航向;当误差逐渐变小时，会通过减小舵面角度来稳定航向。根据以上原理，本文设计了一种动态模糊神经网络，根据e(t)和g′(t)来确定闭环系统的极点［6-7］。在上节的分析中，极点由σ 确定，所以模糊神经网络控制器的输出为σ。则根据图1，可将神经网络部分与模型控制系统相融合，如图3所示。

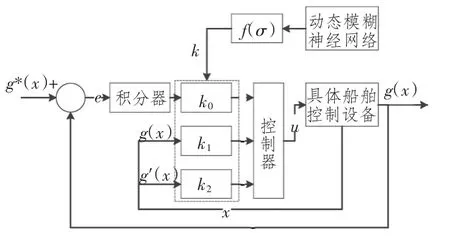
图3 航向控制系统整体结构图Fig.3 Architecture of course control system

采用乘积推理机、单值模糊器和中心平均解模糊公式获得模糊控制器输出。如下式:

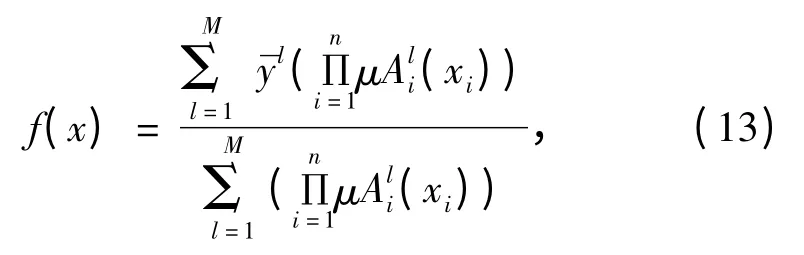
图4 神经网络结构图Fig.4 The structure of neural network

以上模糊神经网络包含模糊器、推理机、解模糊器3个部分［8］。具备了神经网络模型之后，首先需要设计模糊器。令10°为最大容忍误差，则可得以下公式:

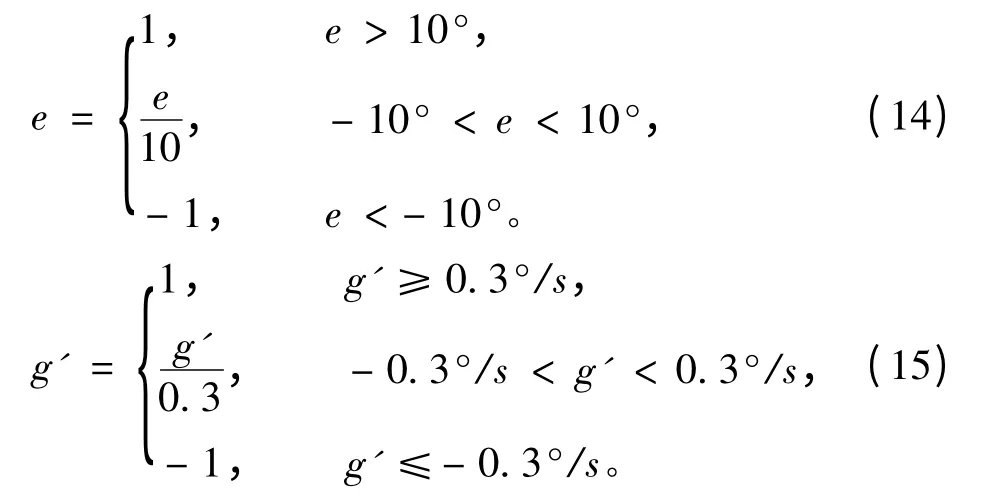
通过归一化之后，e和g′取值均在［-1，1］中，e和g′的隶属度如图5所示。

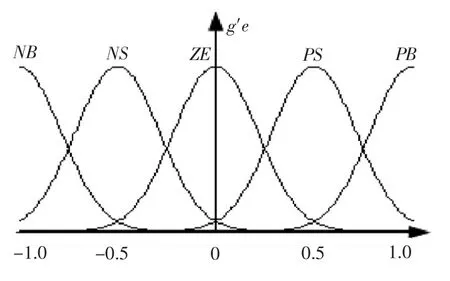
图5 g′与e的隶属度图示Fig.5 The membership of e and g′

分析式(14)和式(15)可知，e和g′被均分为5个域，则输入平面被均分为25个域。其中的有效域如图6所示。

图6 输入平面中y的有效域Fig.6 The effect field of y in input plane

表1 y的最终值Tab.1 Final value of y

4 实验验证

根据图3所示的结构图，本文设计并在Matlab中对基于船舶控制模型和动态神经网络的航向控制系统进行了实验验证。在平稳海域中，对于航向控制的结果如图7所示。根据实验数据，在航向调整角度为30°时，幅度偏差值为5%。这一性能表现证明，本文提出的混合航向控制器能够满足实际需求。

图7 系统性能表现Fig.7 The performance of the system

与纯船舶模型控制方法相比，本文提出的混合方法控制器，不仅能够提供更加灵活的反应水平，并且还具有较小的调整偏差。主要原因是通过动态模糊神经网络，能够产生不同的比例系数σ。当航向误差很大时，神经网络的输出同时增大。在输出变大的同时，其输出同时受到误差值和航向变化率的制约，使得调整的偏差值较小。

5 结 语

通过分析在狭窄海域中，船舶控制的实际问题，本文提出了一种混合船舶控制器，其采用的控制方法结合了船舶模型控制方法和动态模糊神经网络。一方面能够通过模型控制方法得到较好的可靠性和可实现性，另一方面能够通过神经网络的实时反应，提供较好的灵活性和精确性。本文设计了相应的模型结构和数学模型，并利用实验验证了本文提出的方法，通过与纯模型控制方法相比较，证明了本文提出方法的灵活性和精确性。

［1］EDA H.A study of ship handling performance in restricted waters:Development and validation of computer simulationmodel［J］.Trans.SNAME，1986(94):77-85.

［2］ZHANG Rong-jun，CHEN Yao-bin，SUN Zeng-qi，et al.Path control of a surface ship in restricted waters using sliding mode［J］.IEEE Transactions on Control Systems Technology，2008(4):722-732.

［3］ZHOU Bo，CAI Feng，ZHANG Yong-sheng.The design and simulation of a fuzzy controller for course keeping［J］.Ship Science and Technology，2004，26(3):26-27.

［4］何祖军.船舶模糊航向控制器［J］.舰船科学技术，2008，30(6):58-61，65.HE Zu-jun.Fuzzy controller for ship′s course steering［J］.Ship Science and Technology，2008，30(6):58-61，65.

［5］LEE G，SURENDRAN S，KIM S.Algorithms to control the moving ship during harbour entry ［J］.Applied Mathematical Modelling，2009，33(5):2474-2490.

［6］LIU Yi-jian.The design of model reference fuzzy adaptive controller for ship heading ［J］.Control Theory and Applications，2003，22(5):11-14.

［7］HE Zu-jun.Ship′s course steering controller based on adaptive neural fuzzy inference system［J］.Ship Engineering，2008，30(6):46-49.

［8］ZHUO Y，HEARN G E.Ship inteligent autopilot in narrow water［C］//Proceeding of the 27th Chinese Control Conference，2008:243-248.