非线性特性在船舶电力系统中的研究及仿真

王 超，王 刚

(沈阳工程学院，辽宁 沈阳110136)

0 引 言

船舶电力系统的稳定性是指在航行过程中系统受到干扰(如绝缘故障﹑系统负载瞬间突变以及海水乳浊等)时，系统各支路发电机是否能够在一定范围内保持同步，并提供稳定频率的电压。由于现代船舶电力系统结构越来越复杂，负载分支也越来越多，导致船舶供电稳定性更加重要。

船舶电力系统属于一类非线性控制系统，同时随着现代控制理论的发展，系统的自动化程度不断提升，与传统的机械发电不同，现在大部分已采用自动化发电方式，这就对电力系统的稳定性提出更高要求。

本文首先研究了系统支路负载与发电机组的非线性特性，基于鲁棒性控制原理，建立了非线性数学模型，反映了整个支路负载与发电系统耦合特性以及负载动静态过程。

最后，本文提出了一种利用Hamilton 函数方式的并联电力非线性控制系统，通过预置系统状态以及运行状态反馈系统非线性特征系数来调节系统的连续性及稳定性，并通过仿真验证了系统的有效性。

1 船舶电力系统的非线性原理

1.1 电力系统非线性特性

一般船舶电力系统主要由变电器﹑连接电缆﹑发电源机组﹑中央控制器以及配电装置组成，是一个异构复杂的非线性结构。而电路中每个元器件特性各不相同，对元器件的单独分析是不现实的，所以对整个系统的非线性以及造成供电系统不稳定的主要元器件进行分析成为主流。

现在，根据船舶电力系统不同的负载模型，对系统的非线性数学模型主要有以下3 种:网络降阶模型﹑普通简化模型﹑网络保留结构。本文主要对网络降阶模型进行研究。

假设在稳态过程中，发电机组的输出功率保持不变，电力系统负载可用接入中性点的相同阻抗来代替，n 台发电器组可以等效为带有n个电源节点的网络，因此n 台发电器组构成的电力系统的数学模型可以用一个2n 阶的非线性偏微分方式来表示，如图1 表示为n 组多电机系统的网络结构图，图2为其数学模型。

图1 多发电机组电力系统Fig.1 Multi generator power system

图2 电力系统数学模型Fig.2 The mathematics model of power system

整个系统将负载节点、发电机内部电路、发电机端口电路进行整体建模，图2 中f(∂，V)函数为非线性，且在各种状态下满足二阶摆动方程f(∂，V)=。通过对网络结构的数学模型分析可以得到影响系统稳定的关键元器件动态特性。

1.2 船舶电力系统的非线性控制

现代船舶电力系统对于非线性控制一般有以下2 种方式:

1)将相同型号发电机组构成的电力系统近似线性化，依据H∞线性控制理论，采用自动化控制技术与PID控制相结合来控制发电机在负荷变化条件下的电压幅值及频率稳定性。

2)采用理想建模方法精确描述电力柴油机转速与供电电压之间的相互关系，建立船舶电力柴油机的非线性模型，同时将非线性模型等化为H∞线性控制、励磁控制及反馈系统控制器共同控制供电系统的稳定性。图3 给出了此种方式的船舶电力系统非线性控制结构。

图3 船舶电力系统的控制结构图Fig.3 The control structure diagram of ship power system

2 动态负载船舶电力系统数学模型

2.1 柴油发电机组的同步输出功率

将图1 中发电机端口电路电压U 分为d，q 方向的2个分量，表达式如下:

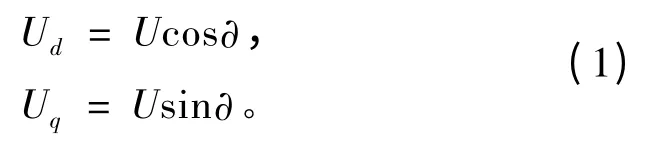
现实中各电网供电系统之间距离较短，传输电缆的电压幅值及频率较低，传输电缆阻抗及变频器阻抗可近似为零，则发电机电流如下:

其中Eq为不加负载时发电机电势。

系统稳态时的电势E′q与Eq之间的联系为:

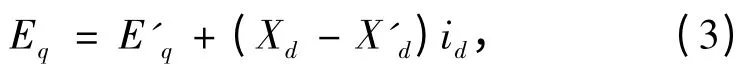
船舶三相发电机组的输出功率为:

同时由于船舶电力系统发电机组都是同步发电，Xd≠Xd，将式(2)中的id，iq代入式(4)，可得到有功功率输出方程:

柴油发电机功率角度∂与其电转速ω 之间有如下关系:

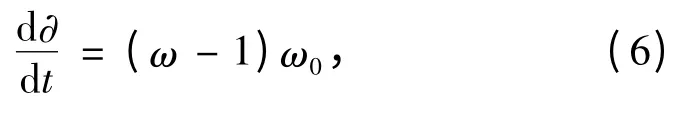
其中ω0为稳态时的初始转速。将式(6)代入式(5)并结合算式(2)和式(3)，即可得到柴油发电机组非稳态下的非线程数学方程:

2.2 柴油发电机组分散励磁系统描述

船舶电力结构中的励磁控制器在整个非线性系统中的位置如图1所示，现在对其一般采用三阶数学模型分析，并且假设发电机电子转速恒定，且忽略非稳态的凸极情况，则励磁控制器暂态方程如下:

将式(7)代入此方程得到其动态方程:

联系式(8)和式(9)，可得到分散励磁控制系统的三阶数学方程如下:

2.3 船舶电力系统的动态负载描述

现在船舶由于其容量越来越大，电路系统的负载容量也越加庞大，负载主要由永磁同步电机及螺旋设备组成。

永磁同步电机同样采用d－q 坐标描述，理想状态下有如下假设:

1)永磁电机磁路消耗忽略，并且电机没有强阻尼干扰。

2)三相电机的电压及电流相等。

3)永磁电机的磁体不会衰变。

则它在d－q 坐标下的电压方程如下:

式中rS为定子电阻;np为极对数;ωr为发电转子转速;φd和φq为磁体的坐标分量。

船舶动力系统的负载可用如下方程表示:

式中Lm为d－q 坐标下励磁电感;φ 为永磁体产生的磁场;M 为负载转矩;J 为转子定量;B 为系统阻尼大小。

3 Hamilton 方法控制系统及仿真

3.1 Hamilton 方法非线性控制描述

船舶电站的非线性控制系统结构如图4所示。

图4 是基于Hamilton 函数非线性控制思想，整个控制系统采用先分后合，分为暂态稳定以及动态系统，同时采用Hamilton 方法设计控制器使得系统中影响供电稳定的主要器件保持恒定，提高系统的暂态稳定性，算法如下:

1)Hamilton 函数输入(u，y)为一阶输出，则整个控制系统稳态子状态方程如下:

式(13)为控制器输出的电压u1的零暂态方程。

2)设计控制器的电压u1使得上式中内部保持恒定，同时需要设计励磁控制器u2，使整个船舶电力非线性控制系统达到动态平衡。根据鲁棒理论，系统平衡的评价如下式:

上式q1和q2为权重因子，用来调节输出电压稳定。

3)令x1=e1，取得虚函数=-ce1，同时V1，可得下式:

5)最后取得基于Hamilton 函数方法的控制器u 公式:

3.2 算法仿真

船舶柴油发电的功率值为1 250 kW，机组转速为n=1 500 r/min，额定传输距离为11.9 kN·m，同步发电机组三相电压390 V，电流为2 310 A，因子系数为0.8，励磁控制系统电压83 V，电流为7.7 A，各参数如表1～表4所示。

表1 发电机参数Tab.1 Parameters of generator

表2 系统参数Tab.2 System parameters

表3 负载电子器件参数Tab.3 Parameters of electron device

表4 非线性控制参数Tab.4 Nonlinear control parameters

图5 给出了仿非线性控制方法的负载功率仿真曲线。

通过图5 可以看到，控制系统随着时间的推移不断的改善了发电机输出电压的品质，该控制系统在船舶电力系统中具有较强的动态稳定性。

图5 仿真曲线图Fig.5 The curve of simulation result

4 结 语

本文首先研究了现代船舶电力系统的非线性原理及特性，随后详细描述了动态负载非线性数学模型，以及支路负载与系统非线性的耦合，同时给出了柴油发电机分散励磁控制系统描述。

最后本文给出了一种基于Hamilton 函数方法的船舶非线性电力控制系统，详细了描述了此方式算法步骤，并通过仿真证明了该方法的有效性。

［1］ZHAO Jie-mei，MENG Jie，ZHANG Li-jun.Passivity-based sliding mode predictive control of discrete-time singular systems with time-varying delay［C］//IEME 2011.

［2］ISHIMARU M，YOKOYAMA R，SHIRAI G，et al.Robust thyristor-controlled series capacitor controller design based on linearmatrix inequality for a multi－machine power system［J］.Electrical Power Energy Systems，2002，24:621－629.

［3］都绍裘.非线性波阻及船型优化研究［J］.舰船科学技术，1994(6):1－5.

［4］张冰，姜长生.舰船在水平面运动中非线性模型的建立［J］.舰船科学技术，2005(5):25－27.

［5］ESEOBAR G，SIRAR H.A Passivity based-sliding mode control approach for the regulation of power faector precompensators［J］.Decision and control，1998(3):2423－2424.

［6］钱佳，何祖军.船舶动力定位非线性自适应滤波算法［J］.舰船科学技术，2013(12):25－28.

［7］JASWANTH C，RANJITH M，ASAD Davari Edge detection and segmentation formachine vision［C］//IEEE，2005:457－461.