基于五块模式的单一矩形件排样算法

易向阳， 潘卫平， 张俊晖

(1. 广西大学计算机与电子信息学院，广西 南宁 530004；2. 四川信息职业技术学院，四川 广元 628017)

基于五块模式的单一矩形件排样算法

易向阳1， 潘卫平1， 张俊晖2

(1. 广西大学计算机与电子信息学院，广西 南宁 530004；2. 四川信息职业技术学院，四川 广元 628017)

如何在一个大矩形里排入尽可能多的单一规格小矩形件是广泛出现在制造业领域的板材分割、物流业领域的集装箱装载中的问题。采用五块模式将大矩形划分为五个块，求解每个块里面矩形件的排样方式。首先，采用动态规划算法一次性生成所有块中矩形件排样方式，然后，采用隐式枚举法考虑所有可能的五块组合，选择包含矩形件个数最多的五块组合作为最终的排样方案。使用算例对算法进行了测试，并与另外4种单一排样算法进行了比较。实验结果表明，该算法在排样利用率和切割工艺两方面都有效，而且计算时间合理。

矩形排样问题；动态规划算法；隐枚举；五块模式

本文讨论单一矩形件排样问题[1]：在尺寸为(L：长，W：宽)的大矩形中排入尺寸为(l，w)的小矩形件，优化目标是使得排入的矩形件个数最多。该问题有2个主要的应用领域[2-4]：①下料领域，将矩形板材分割成最大数量的同种矩形件，提高材料利用率；②物流领域，用来确定托盘装载、货运装载、

集装箱装船方案，充分利用装载区域。为了叙述方便，本文主要采用下料领域的术语。该问题看似简单，其实不然，文献[5]认为该问题是高计算复杂度的NP难问题。目前国内外已有一些学者分别提出了近似算法来解决此问题。其中最著名的当属Agrawal单一排样算法[6]，该算法能生成最优剪切排样方案。由分析可知，当使用气焰分割技术分割板材时，排样方案并不需要满足剪切工艺要求，另外物流领域的托盘装载方案显然不需要满足剪切工艺要求。鉴于此，本文对Agrawal单一布局算法进行扩展，使其能够生成排样利用率更高的非剪切排样方案。

本文提出了基于五块模式的单一矩形件排样算法。采用动态规划和隐式枚举法相结合来求解排样方案，并通过实验验证该算法的有效性。

1 相关概念

1.1 规范多级方式

定义 1. 条带和级。若干个矩形件排列在一起组成条带[7]，条带分X向条带(图1(a))和Y向条带(图1(b))两种类型。条带的宽度等于矩形件的宽度，长度等于矩形件个数与矩形件长度之积。若干根方向相同的条带组成级，级的方向由其中的条带方向决定，包含X向条带的级为X向级(图2(a))，包含Y向条带的级为Y向级(图2(b))。

图1 条带

图2 级

定义2. 规范多级方式。图3所示为规范多级方式图，每个级按照剪切时被切下的先后顺序进行编号。其中，所有奇数级具有相同的方向，所有偶数级具有相同的方向，且奇数级与偶数级方向垂直[8]。崔耀东和周儒荣[9]已证明任何可以剪切下料的排样方式都可以在矩形件个数不减少和级数不增加的情况下等价转换为规范多级方式。

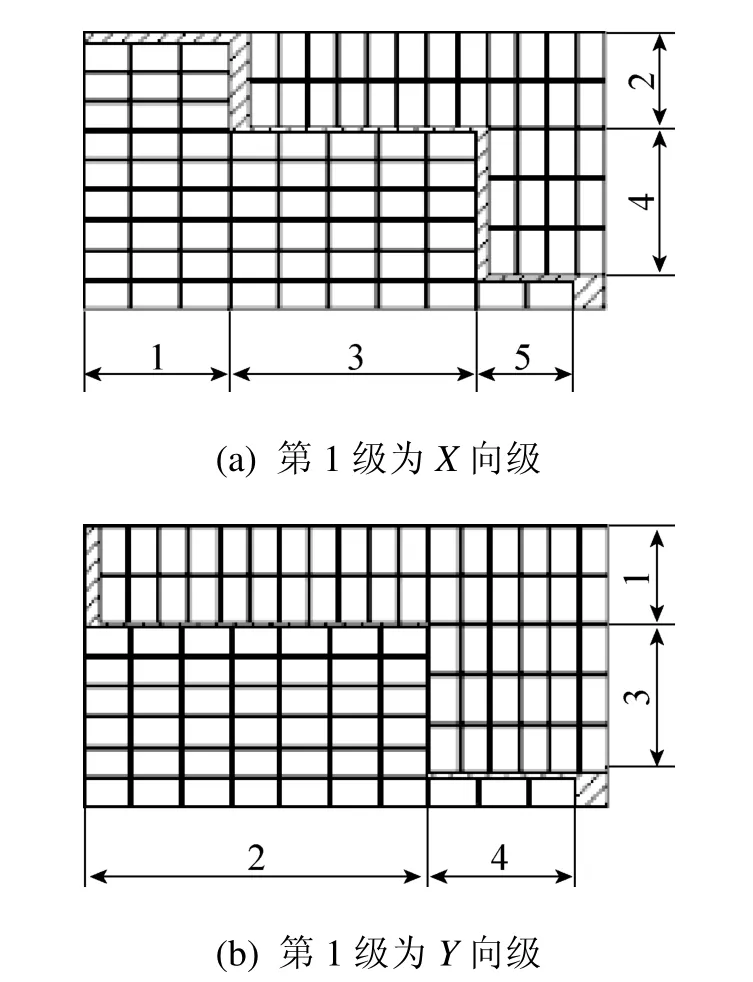
图3 规范多级方式

1.2 五块模式

五块模式由5个块组成，每个块里面的矩形件都按照规范多级方式进行排放。块的划分见图4，其中板材长为 L，宽为 W。从图中可以看出：块1(x1,y1)(长为 x1，宽为 y1)、块 2(x2,y2)、块块其中x1,y1均大于0，。需要指出的是：本文的五块模式和文献[10]五块方式是不同的，文献[10]中每个块里面是由若干排水平矩形件和若干排竖直矩形件的简单组合。而本文每个块里面矩形件是按照规范多级方式排放的，规范多级排样方式是前者的超集。

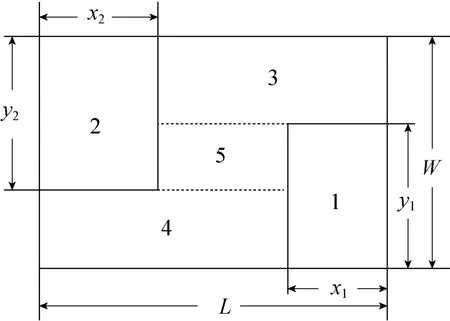
图4 五块模式图

如图5所示，块1中包含一个Y向级，块2中包含一个Y向级，块3中包含一个X向级和一个Y向级，块4中包含一个X向级，块5中为空。

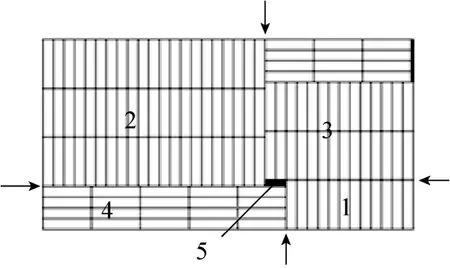
图5 单一矩形件五块排样方案

2 算法原理及其实现

假定板材尺寸和矩形件尺寸都为整数。对于规格为(L, W)的板材，假设L ≥ W。

2.1 确定块的规范多级方式

对于块(x,y)，x≤L，y≤W。规范多级方式的排样过程可看作是一系列的条带拼接过程，如图6所示每次总是沿着当前方式的水平边或竖直边拼接上一根条带，最终形成整块上的排样方式。设F(x,y)为块(x,y)中所能排放的矩形件个数。则有如下递推公式：

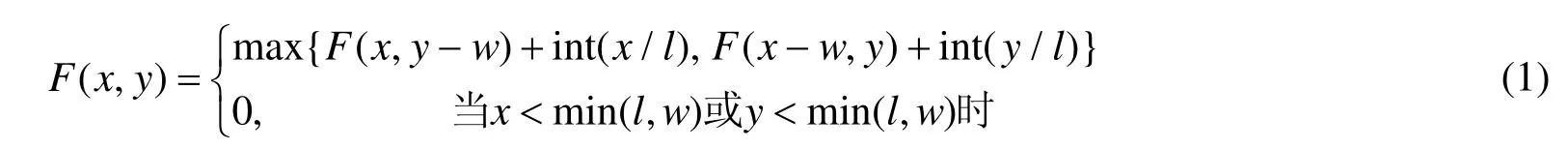
采用如下的动态规划算法[8]生成所有块的规范多级方式：

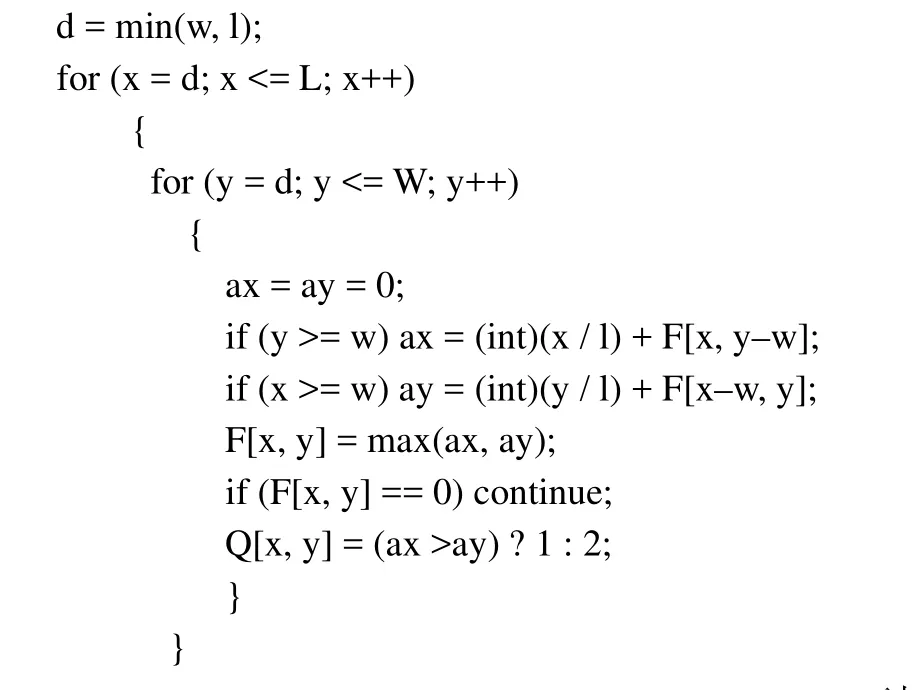
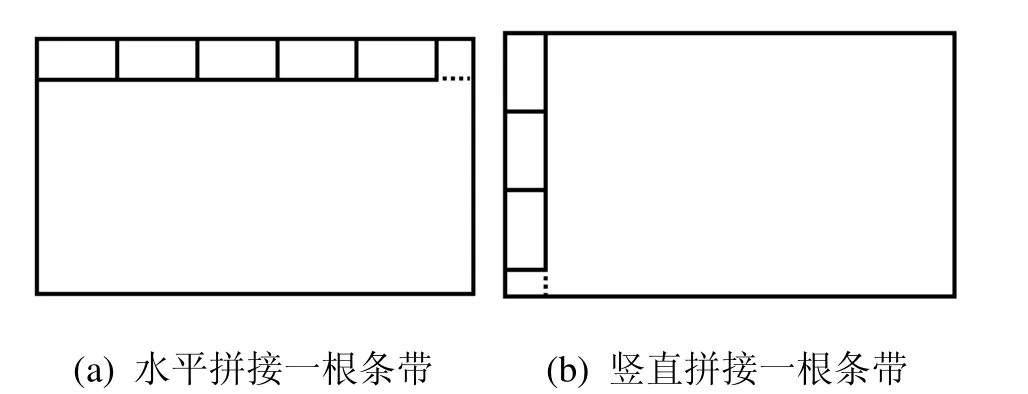
图6 条带的两种拼接方式

2.2 块的规范尺寸

规范尺寸概念已经被许多学者使用在排样问题中[11]，使用规范尺寸可以减少算法中不必要的计算开销。设a为规范尺寸，则：a= n1l+ n2w, 0 ≤ a ≤ L，n1,n2均为非负整数 (2)

令A为规范尺寸集合，n为集合A的元素个数。规范尺寸有如下性质：假设 A(x)为不大于x的最大规范尺寸，则有 F(x,y)=F(A(x),A(y ))。

2.3 确定五块排样方案

设五块排样方案排放的矩形件个数为M。则有如下公式：

其中，x1、y1、x2、y2如图 4所示，且均在集合 A中取值。该算法时间复杂度为 O(n4)。由于n远远小于L，故运用规范尺寸概念可以明显地降低算法时间复杂度，减少计算时间开销。

2.4 最优五块排样算法

步骤 1. 输入板材和矩形件尺寸数据；

步骤 2. 根据 2.1节所述算法确定所有可能尺寸的块的规范多级排样方式和排入的矩形件个数；

步骤 3. 根据式(2)确定集合A；

步骤 4. 根据式(3)用隐式枚举法确定 x1、y1、x2、y2，并得到最终的五块排样方案。

3 实验计算

目前尚没见到有关于单一矩形件五块排样算

法的报道。实验通过4组测题将本文排样算法分别与Agrawal单一排样算法、文献[8]单一排样算法、文献[12]二划分排样算法、文献[2]启发式排样算法进行比较，其中前3种算法属于剪切排样算法，第4种算法属于非剪切排样算法。用C++语言实现本文算法，在VC6.0平台上进行实验。实验所用计算机为Inter(R) Pentium(R) CPU G630，主频2.7 GHz，内存2 GB。

3.1 与Agrawal单一排样算法比较

随机生成100道排样例题，每道例题使用不同的板材和矩形件尺寸，表1所示为各变量均匀分布的范围。表2为计算结果总结。从表2可以看出，本文算法在计算时间合理的前提下，平均排样利用率比Agrawal算法提高了1.58%。图7为其中一道例题在两种算法下的排样方案，板材长为200 cm，宽为100 cm，矩形件长为17 cm，宽为7 cm，Agrawal算法生成的排样方案板材能排入165个矩形件，本文算法生成的排样方案板材能排入168个矩形件。

表1 实验数据分布范围(cm)

表2 计算结果

图7 两种算法生成的排样方案

3.2 与文献[8]单一排样算法比较

采用文献[13]数据，含10道测题。矩形件尺寸均为(长320 mm，宽180 mm)，板材长宽尺寸的取值范围均为(800～3 000 mm)。表3为10道测题的计算结果。记文献[8]算法生成的排样方案包含的矩形件个数为N1，参见文献[13]的表1。记本文算法生成的排样方案包含矩形件个数为N2。图8为测题4在两种算法下的排样方案。

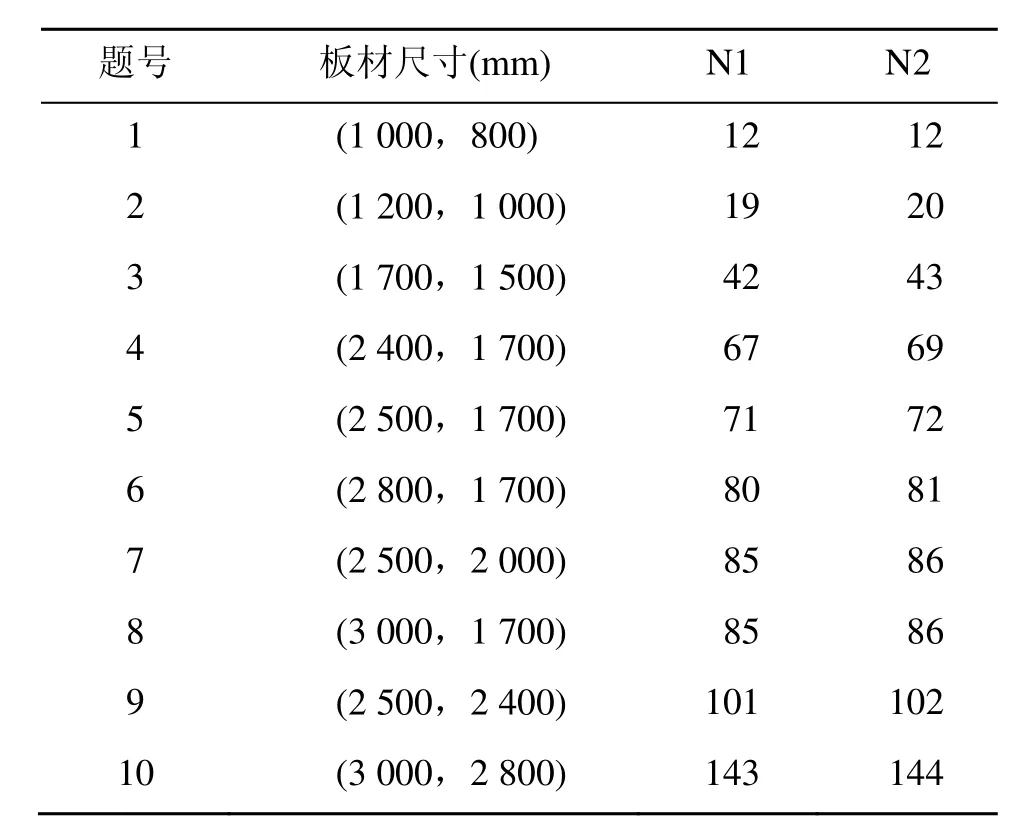
表3 10道测题的实验结果

3.3 与文献[12]二划分排样算法对比

采用文献[12]例题2数据，板材长为3 000 mm，宽为2 000 mm；矩形件长为166 mm，宽为91 mm。文献[12]二划分装盘递归算法生成的排样方案可排入394个矩形件，本文算法生成的排样方案如图9所示，可排入396个矩形件。

3.4 与文献[2]启发式排样算法对比例题：如何用长为300 cm，宽为200 cm的板材切割出最多数目的长为21 cm，宽为19 cm的矩形件？本文算法生成的排样方案如图 10所示，包含149个矩形件。文献[2]算法生成的排样方案也包含149个矩形件。但两种排样方案相比，本文排样方案显著简化了切割工艺。

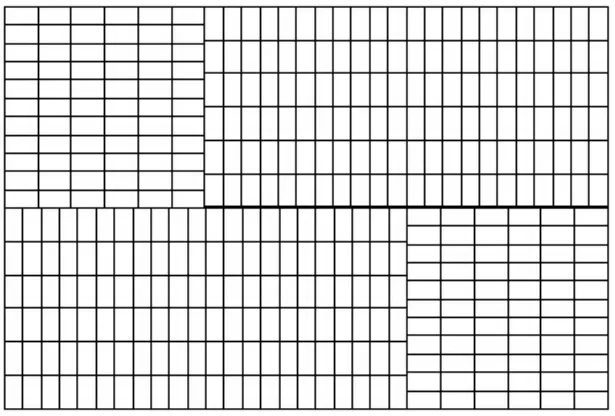
图9 采用文献[12]例题2数据，本文算法生成的排样方案

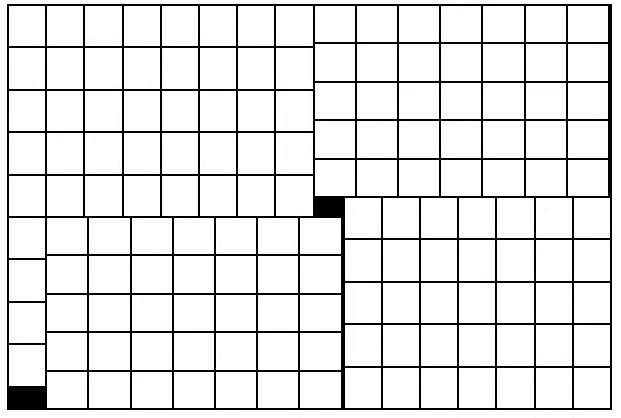
图10 例题用本文算法生成的排样方案

4 结 束 语

本文提出了非剪切方式的单一矩形件五块排样方案，并采用动态规划和隐式枚举算法生成该种排样方案。算法时间复杂度低，设计思路简单明了，便于编写相应软件时应用参考。与剪切方式排样算法相比，本文算法能够生成排样利用率更高的排样方案。与非剪切排样算法相比，本文算法生成的排样方案能够显著地简化切割工艺。将本文算法应用在集装箱装运领域，生成的排样方案能够较好地提升装载空间利用率，简化装载操作。

[1] Birgin E G, Lobato R D, Morabito R. An effective recursive partitioning approach for the packing of identical rectangles in a rectangle [J]. Journal of the Operational Research Society, 2010, 61(2): 306-320.

[2] Scheithauer G, Terno J. The G4-heuristic for the pallet loading problem [J]. Journal of the Operational Research Society, 1996, 47(4): 511-522.

[3] Wäscher G, Haußner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[4] Lu Yiping, Cha Jianzhong. A fast algorithm for identifying minimum size instances of the equivalence classes of the pallet loading problem [J]. European Journal of Operational Research, 2014, 237(3): 794-801.

[5] Letchford A N, Amaral A. Analysis of upper bounds for the pallet loading problem [J]. European Journal of Operational Research, 2001, 132(3): 582-593.

[6] Agrawal P K. Minimising trim loss in cutting rectangular blanks of a single size from a rectangular sheet using orthogonal guill otine cuts [J]. European Journal of Operational Research, 1993, 64(3): 410-422.

[7] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.

[8] 崔耀东. 计算机排样技术及其应用[M]. 北京: 机械工业出版社, 2004: 94-125.

[9] 崔耀东, 周儒荣. 冲裁件有约束最优剪切方式的设计[J]. 数学的实践与认识, 2001, 31(2): 177-184.

[10] Bischoff E, Dowsland W B. An application of the micro to product design and distribution [J]. Journal of the Operational Research Society, 1982, 33(3): 271-280.

[11] 季 君, 陆一平, 查建中, 等. 生成矩形毛坯最优两段排样方式的确定型算法[J]. 计算机学报, 2012, 35(1): 183-191.

[12] 孙 英, 何冬黎, 崔耀东. 生成最优二划分装盘方案的递归算法[J]. 计算机仿真, 2009, 26(9): 160-163.

[13] 杨少杰, 崔耀东. 同尺寸矩形毛坯排样算法[J]. 桂林理工大学学报, 2012, 32(4): 628-630.

Algorithm for Generating Five Block Mode Cutting Patterns of Single Rectangular Items

Yi Xiangyang1, Pan Weiping1, Zhang Junhui2
(1. Computer and Electronic Information College, Guangxi University, Nanning Guangxi 530004, China; 2. Sichuan Institute of Information Technology, Guangyuan Sichuan 628017, China)

It is widely appears in manufacturing field of plate segmentation and the logistics industry field of pallet loading that how to finding a maximal layout for identical small rectangles on a larger rectangle. The large rectangle is divided into five blocks using five-block mode, then the problem is solved to arrange the identical small rectangular into each blocks. Firstly, the dynamic programming method is used to generate the entire layout of rectangular in blocks in once. Then, the enumeration method is used to consider all of five blocks combination. The combination is selected to generate the final pattern which have the maximal number of rectangular. Several examples are used to test the proposed algorithm, and comparing the algorithm with other 4 kinds of single layout algorithm. The experimental results show that the algorithm is efficient in both the layout utilization rate and the cutting process with a reasonable computing time.

rectangle packing problem; dynamic programming algorithm; implicit enumeration; five block mode

TP 391

A

2095-302X(2015)04-0521-05

2014-10-29；定稿日期：2015-01-21

国家自然科学基金资助项目(61363026，71371058)；广西高等教育教学改革工程重点资助项目(2013JGZ110)

易向阳(1973–)，男，广西桂林人，讲师，硕士。主要研究方向为优化计算技术与CAD。E-mail：3106868978@qq.com

张俊晖(1983–)，男，四川合川人，讲师，本科。主要研究方向为优化计算技术和程序开发。E-mail：2228462300@qq.com