平面简单闭合曲线离散采样与重建算法

范丽鹏， 王丽英， 庞明勇

(南京师范大学教育技术系，江苏 南京 210097)

平面简单闭合曲线离散采样与重建算法

范丽鹏， 王丽英， 庞明勇

(南京师范大学教育技术系，江苏 南京 210097)

提出一种鲁棒的平面简单闭合曲线离散采样与重建算法。算法分为采样过程和重建过程两部分。采样部分首先对平面闭合曲线均匀取点，然后计算各点到曲线所围平面区域中轴的最近距离，最后根据所求距离确定采样间隔，获取采样点集；重建部分首先构建采样点集的Delaunay三角剖分，然后从得到的三角形中选择边构建初始化图形，最后通过修改该图形获得重建图形。实验表明算法得到的采样点较少且能反映曲线的局部几何特性，重建图形能够较好地表示原闭合曲线的形状及走向。

曲线重建；离散采样；无序点集；平面图形

在图形建模与几何处理领域中，有关三维形体离散采样与曲面重建的研究已开展得非常深入[1-2]。相对而言，平面曲线采样与重建的研究工作大多集中于传统的样条曲线方法[3-4]，而基于计算几何方法的研究文献相对较少；另一方面，在图形图像技术的现实应用中，有许多操作涉及对各类曲线进行采样与重建等计算[5]。因此对基于计算几何方法的曲线采样与重建进行研究，具有重要的意义。

目前，对平面曲线进行离散采样的方法主要有3种：①栅格法[6]，首先将曲线所在的平面区域栅格

化，然后将曲线与栅格线的交点作为离散采样点。由此得到的采样点通常数据量较大，且采样点集不能很好地反映曲线的局部几何特性；②预测投影法[7]，即从曲线的某点开始，根据曲线在该点处的曲率大小，沿该点的切线方向前进一小段得到预测点，然后将预测点投影到曲线上得到采样点。由于该方法包括了一个投影过程，所以计算量较大；③ε-采样法[8]，其处理对象为平面闭合曲线，采样条件为：设曲线上一点到采样点的最近距离为 d1，到曲线所围平面区域中轴的最近距离为 d2。若一采样点集使曲线上任意一点满足 d1＜ε× d2，则其为所求点集，ε取值范围为 0 ＜ε＜ 1。由于该方法设定了参数ε，对于不同的图形均需要找到合适的ε值，才能满足采样条件，因此获取的采样点集充满了不确定性。

平面曲线重建算法主要包括：文献[9]提出了基于最小二乘法的平滑曲线重建，该方法通过对噪声采样点集进行滤噪来实现平滑曲线的重建，其主要关注点是如何过滤采集数据中的噪声；Amenta等[8]提出了基于β骨架与Voronoi图的Crust算法，该算法先求取原始点集的Voronoi图顶点，再对原始点集以及得到的顶点集进行Delaunay三角剖分，最后通过选取三角剖分中三角形的边来进行曲线重建。该方法对原始点集的密度要求严格；Dey等[10]对该算法进行了改进，降低了对原始点集密度的要求。上述算法的重建对象是简单的闭合光滑曲线，Althaus和Mehlhorn[11]进一步对算法进行了扩展，使之能够处理开放曲线，Dey和Wenger在文献[12]中给出一种能够处理多尖角图形的算法变种。上述算法均需设定采样参数，即对于不同的图形均需找到合适的参数值，才能获得适合其重建算法的采样点集。

本文给出一种针对平面简单闭合曲线的采样与重建算法。其中采样过程不需要设定参数，并且所得采样点集较少且能较好地重建原始曲线。

1 算法梗概

本文算法由采样与重建构成。采样过程是由平面简单闭合曲线(图1(a))得到表示该曲线的稀疏点集(图1(b))；重建则由上述采样过程所得到的采样点集重建逼近原曲线的重构图形(图1(c))。

采样过程的主要步骤：

(1) 计算曲线所围平面区域的中轴。中轴上任意一点，与被采样曲线均存在两个或两个以上距离相等的点[13]。

(2) 对曲线均匀取点，并计算各点的局部特征大小。所谓的局部特征大小，是指点到中轴的最近距离[14]，如图2(a)、(b)所示。

图1 曲线的采样与重建

图2 矩形与圆的中轴、特征大小及采样点

(3) 获取采样点。依据上述所求的局部特征大小，确定采样间隔，获取采样点集，图2(c)中圆心点即为采样点。

(4) 添加采样点。图2(c)中两圆相交点为可增加点。最终所得采样点集只需从可增加点中选择部分点添加到上述采样点集中即可。

曲线重建过程的主要步骤：

(1) 逐次连接采样点集(图3(a))中距离最近的点，使其连成一个闭合图形，并且使得该图形中每个点至少连接两条边，如图3(b)所示。

(2) 求点集的凸包，如图3(c)所示，并求取图3(b)的边界，如图3(d)中实线所示。其中，虚线为删除的上述图形(图3(b))中的边，实线为所求边界；边界内部的点，即图3(d)中两条虚线相交的点，不属于边界点。

图3 曲线重构示意图

(3) 修改上述边界中邻边个数大于2的点，使得其邻边个数为2或0，如图3(e)所示。图3(d)中圆内的点即为邻边个数大于2的点。

(4) 将邻边个数为0的点连接到修改后的边界中，使其邻边个数为2，如图3(f)所示。图3(e)中圆内的点即为邻边个数为0的点。

2 采样过程

2.1 计算中轴

本文采用文献[15]的方法提取平面封闭区域的中轴。该方法提出了一种基于Voronoi图[16]的中轴提取方法，利用Voronoi图顶点的连线模拟中轴。由于Voronoi图的顶点为图中边的交点，且边为曲线上相邻点连线的垂直平分线，所以Voronoi图顶点属于中轴点。进而将平面闭合曲线看作是一些点的集合，当点集足够密时，其Voronoi图顶点的连线即可逼近曲线所围区域的中轴。

2.2 计算局部特征大小

对原始曲线(图4(a))均匀取点，然后计算各点到曲线所围平面区域的中轴(图4(b)中紫线)的最近距离，并将该距离记为该点的局部特征大小。由图2(c)所示，在曲线上曲率较大的地方，点的局部特征较小，而在曲线较为平滑的地方局部特征较大。因此，根据曲线上所取各点的局部特征大小可获得较少且能表示曲线局部几何特性的采样点集。

2.3 获取采样点

2.4 增加采样点

由于所得采样点不能较好地重建曲线，因此需要添加采样点。添加条件：以任意采样点p为圆心，以该点到其相邻采样点的距离为半径画圆，若在圆内或圆上存在与p不相邻的采样点q，则在点p与该相邻采样点之间添加可增加点。为了使得添加的点数量较少，可通过设置一个数值，使得当p与q之间的采样点与可增加点的个数小于该数值时，不执行操作。若该数值设置过大，则使得添加点过少，而不能重建图形，若该数值设置过小，则会添加多余的点。因此需要不断测试寻找到一个合适的数值，测试方法：首先设数值为1，即 q点不存在，然后获取采样点集，再对采样点集进行重建，若重建图形能够很好地逼近原曲线，则继续增加数值，直到所生成的采样点集不能很好地重建曲线为止，则取前一数值为所求数值。由于文中采样算法和重建算法是顺次执行的，因此对于不同图形，可由计算机自动地判定合适的取值大小。实验表明，多数图形的数值可取6，且所得到的采样点集更为稀疏且能很好地重建原曲线，图4(e)中红色的点即为所增加的点。

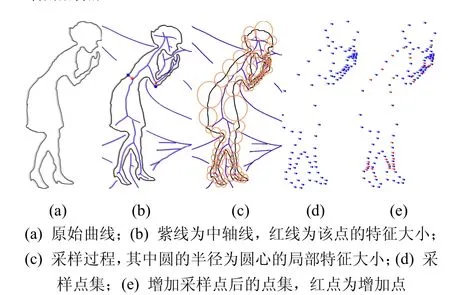
图4 采样过程

3 重建过程

3.1 构建初始化图

首先构建采样点集的Delaunay三角剖分[17]，由于得到的Delaunay三角形集合中存在较多的边，所以需要从中选取部分边来连接采样点集进而重建图形。依据格式塔[18]的连续性和近似性原理可知，重建图形为闭合图形，每个点邻边个数均为2，且所有边长的和最小。在构建采样点集的初始化图过程中，涉及到闭合回路的问题，因此在图5(a)中，展示了非闭合回路的示意图，图5(b)中展示了闭合回路的示意图。

初始状态时，所有采样点均没有相邻边，如图6(a)所示。首先从Delaunay三角形集合(图6(b))中选择长度最短的边，若该边存在邻边个数小于2的端点，则选择该边来连接相应的采样点，否则舍弃；然后再从剩余边中选择长度最短的边进行上述判

断；最后重复执行上述操作，直到所有采样点邻边个数均不小于2为止。此时，所得图形中不存在邻边个数小于2的点，但是该图形可能为非闭合图形，如图5(a)所示，因此需要再次添加边，操作步骤为：先从Delaunay三角形集合中选择长度最短的边，若该边连接两个不连接的闭合回路(图5(b)中最长的线)，则将该边添加到上述非闭合图形，并判断连接后所得图形是否为闭合图形，若不是，则继续选择剩余边中最短的边，并重复执行上述操作，直到整个图形为闭合图形为止，如图5(b)所示。将所得图形记为图形A，如图6(c)中阴影部分所围图形所示。

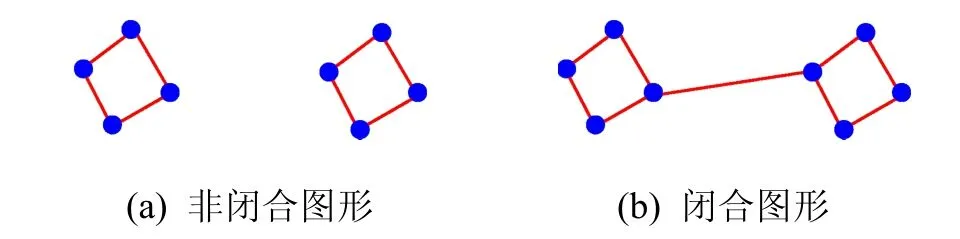
图5 非闭合和闭合图形示意图

3.2 构建初始化图的边界

由于图形A中存在邻边个数大于2的点，因此需要对其进行修改。为了更好地解决这个问题，可以先修改图形A的边界，然后再修改其内部的点。通过删除图形A外部的Delaunay三角形可以求得图形A的边界，图6(c)中空白区域的三角形即为图形A外部的三角形。

为了找到图形A外部的Delaunay三角形，可以先求得图形A的凸包，即一个最小的多边形，其所有点集均在该多边形内部或边上，并且点集中任意两点之间的连线均在多边形内部或边上[19]，如图6(d)中实线所示。获得采样点集的凸包后，逐一删除凸包内部包含凸包的边或新添加的且不为图形A的边的三角形，可获得图形A的边界图形B，如图6(e) 中阴影部分所围图形所示。

3.3 修改边界上的点

由于图形B中可能存在邻边个数大于2的点，如图6(e)所示，所以需要对图形B进行修改，使得图形B中所有点的邻边个数为2或0。

首先找到位于图形B外部且包含邻边个数大于2的点的Delaunay三角形，记为集合T2。对于图3(c)中的点来说，图7(a)中包含边为虚线的三角形即为T2中的三角形。由于存在多个这样的三角形，且添加三角形的先后顺序会影响重建的最终效果，因此可通过对T2中的每个三角形计算被添加后图形B中所有边的长度和的变化量，进而确定T2中三角形被添加的先后顺序。通常优先添加变化量最小的三角形。添加三角形的过程如图7(a)～(c)所示。添加三角形后，可能会出现3种情况：①不满足T2要求的三角形仍然在集合T2中；②满足T2要求的三角形不在集合T2中；③T2中一些三角形的变化量发生了变化。所以要分别对这3种情况进行分析，并针对相应的情况对T2进行删除、添加或修改的操作，直到集合T2为空为止。所得图形记为图形C，如图6(f)中阴影部分所围图形所示。

3.4 修改边界内部的点

由于图形C以及图形B的内部存在邻边个数为0的点，所以需要对其进行修改，使其邻边个数为2。

首先在图形C内部的Delaunay三角形中找到一边在C上且该点邻边个数为0的三角形，记为集合T0，图7(d)中包含边为虚线的三角形即为T0中的三角形。由于T0中存在较多的三角形，且删除T0中三角形的先后顺序会影响最终的重建效果，所以需要对T0中的每个三角形计算被删除后图形C中所有边的长度和变化量，并依据变化量的大小确定T0中各三角形被删除的先后顺序。通常优先删除变化量最小的三角形。删除三角形过程如图7(d)～(e)所示。删除三角形后，会出现2种情况：一种是不符合集合T0要求的三角形仍然存在；另一种是符合集合T0要求的三角形不在。所以要分别对这2种情况进行分析，并针对上述情况对集合T0进行删除或添加。

当集合T0为空时，即获得重建图形，如图6(g)中阴影部分所围图形所示。

图7 添加和删除三角形过程

4 实现与结果

本算法在PC机上运用VC6.0和OpenGL实现了采样过程和曲线重建过程。实验结果如图8所示。其中小松鼠和小白兔在增加采样点时，计算机判定其最适合的数值为6，而海豚的数值为1，它们均展示了由闭合曲线获得采样点集，以及由采样点集重建图形的过程。可以看出，图中的采样点集能较好地反映原曲线的局部几何特性，在距离较近但不相连接处采样比较密集，而在其他处采样比较稀疏。最终所得图形均能够较好地表示原曲线的形状及走向。

图8 松鼠、兔子、海豚采样及重建过程

5 结 束 语

本文给出的基于平面简单闭合曲线的采样与重建算法，成功地实现了平面简单闭合曲线的采样及重建过程。大量实验表明，该算法能够获得更为稀疏且能反映曲线局部几何特性的采样点集，并且利用该点集能较好地重建出原曲线。由于本文算法只是针对简单闭合曲线进行采样与重建，而对于未闭合以及更为复杂的曲线不具有很好的适用性，因此对于上述类型的曲线以及高维空间曲线的采样与重建是今后需要考虑的问题。

[1] 厉玉蓉, 张彩明, 董付国. 三角网格上五次齐次代数曲面的重构[J]. 计算机辅助设计与图形学学报, 2008, 20(9)： 1186-1190.

[2] 庞旭芳, 庞明勇. 点云模型自适应增加采样点算法[J].小型微型计算机系统, 2010, 11(11)： 2265-2271.

[3] 黄童心, 王文珂, 张 慧, 等. 基于场分布的平面散乱点集B样条曲线重建算法[J]. 工程图学学报, 2010, 31(2)： 73-83.

[4] 张 娴, 张志毅, 田素垒, 等. 基于曲率分析的三次Bezier 曲线采样方法的研究[J]. 计算机工程与应用, 2013, 49(5)： 160-162.

[5] 骆 沛, 吴壮志, 夏春和, 等. 基于 e1范数最小化的非流形曲线族重构[J]. 计算机学报, 2013, 36(9)： 1917-1928.

[6] 谭昌柏, 周来水, 安鲁陵, 等. 逆向工程中基于密集数据点的轮廓线重建技术[J]. 华南理工大学学报, 2005, 33(5)： 32-37.

[7] Akkouche S, Galin E. Adaptive implicit surface polygonization using marching triangles [J]. Computer Graphics Forum, 2001, 20(2)： 67-80.

[8] Amenta N, Bern M, Eppstein D. The crust and the β-skeleton： combinatorial curve reconstruction [J]. Graphical Models and Image Processing, 1998, 60(2)：125-135.

[9] 庞明勇, 卢章平. 局部数据集与噪声数据曲线的平滑过滤[J]. 矿山测量, 2001, (4)： 24-27.

[10] Dey T K, Mehlhorn K, Ramos E A. Curve reconstruction：connecting dots with good reason [C]//ACM. SOCG. Hong Kong, China, 2000： 229-244.

[11] Althaus E, Mehlhorn K. TSP-based curve reconstruction in polynomial time [C]//ACM/SIAM. SODA. San Francisco, CA, USA, 2000： 686-695.

[12] Dey T K, Wenger R. Fast reconstruction of curves with sharp corners [J]. International Journal of Computational Geometry & Applications, 2002, 12(5)： 353-400.

[13] Blum H. A transformation for extracting new descriptors of shape [J]. Models for the Perception of Speech and Visual Form, 1967, 19(5)： 362-380.

[14] Ruppert J. A new and simple algorithm for quality 2-dimensional mesh generation [C]//ACM/SIAM. SODA. Austin, USA, 1993： 83-92.

[15] Karimipour F, Ghandehari M. Voronoi-based medial axis approximation from samples： issues and solutions [M]. Transactions on Computational Science XX. Berlin Heidelberg： Springer, 2013： 138-157.

[16] Aurenhammer F. Voronoi diagrams： a survey of a fundamental geometric data structure [J]. ACM Computing Surveys, 1991, 23(3)： 345-405.

[17] 何 俊, 戴 浩, 谢永强, 等. 一种改进的快速Delaunay三角剖分算法[J]. 系统仿真学报, 2006, 18(11)： 3055-3057.

[18] Ohrhallinger S, Mudur S P. Interpolating an unorganized 2D point cloud with a single closed shape [J]. Computer-Aided Design, 2011, 43(12)： 1629-1638.

[19] 刘 斌, 王 涛. 一种高效的平面点集凸包递归算法[J].自动化学报, 2012, 38(8)： 1375-1379.

Discretely Sampling and Reconstructing Simple Planar Closed Curves

Fan Lipeng, Wang Liying, Pang Mingyong
(Department of Educational Technology, Nanjing Normal University, Nanjing Jiangsu 210097, China)

A robust algorithm is proposed for discretely sampling continuous planar curves and reconstructing the curves from the sampled point sets. The algorithm covers two processes, sampling and reconstruction. In the sampling part, the points are evenly obtained from a given planar closed curve, and then the distances are calculated between each point and the medial-axis of the planar area surrounded by the closed curve. Subsequently, the sampling intervals are decided by the distances and finds the sampling points. In the reconstruction part, a Delaunay triangulation is first built for the sampled points, and then edges are selected from the triangulation to build the initialize graph. Finally, the reconstructed curve is obtained by modifying the graph to a new version. Experiments show that the point sets sampled by our algorithm are locally adapted to the local geometric characteristics of the curves, and the reconstructed curves can approximate the original curves well.

curve reconstruction; discretely sampling; scattered points; 2D graphics

TP 391. 41

A

2095-302X(2015)04-0511-05

2015-01-14；定稿日期：2015-02-25

国家自然科学基金资助项目(41271383，60873175)；江苏省现代教育技术研究课题资助项目(2014-R-33356)；江苏省高校自然科学基金资助项目(11KJB520008)；江苏高校优势学科建设工程资助项目

范丽鹏(1993–)，女，河南南阳人，硕士研究生。主要研究方向为数字几何处理。E-mail：funnypower@126.com

庞明勇(1968–)，男，安徽淮南人，教授，博士。主要研究方向为几何建模与数字几何处理。E-mail：panion@netease.com