静电场与万有引力场的类比探讨*

◆张国前

静电场与万有引力场的类比探讨*

◆张国前

类比是物理学中的一个重要思想方法。在静电场和万有引力场中，从基本的实验定律、宏观特征量的定义、实体性的描述，到主要规律的表述及证明、典型应用等，既表现出很多的相似性，又表现出不同的个性。通过类比，加深对物理概念的深入理解，渗透物理学的思想方法。

静电场；万有引力场；类比

类比法是人类认识客观世界的一种基本思维方法，是根据两个(或两类)对象之间在某些方面的相同或相似而推出它们在其他方面也可能相同或相似的一种推理方法。物理学上许多重要理论，都是通过类比提出假设，然后经过实践检验发展成为科学理论的。其中万有引力场与静电场的发现及其规律的认识，类比的思想方法起了非常积极的作用。

在大学物理教材中，静电场和万有引力场分别在电磁学和力学部分讨论，而且力学是以力为主线展开，没有突出场的特性。如果注意到静电场和万有引力场的联系，应用类比的方法，尽可能还原科学家发现规律及逐渐深化认识的过程，可以帮助学生感受和体会物理科学的闪光思想和方法，并由此及彼，更加深入系统地掌握物理规律，促进学生提高思维能力。

1 奠基性的实验定律

万有引力定律和库仑定律都是人们熟悉的物理规律。万有引力定律最早由牛顿于1685年发表在其名著的《自然哲学的数学原理》一书中。它指出，任意两个质点之间都存在相互作用的引力，定量表达式为：

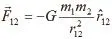
1785年，库仑发现两个静止点电荷之间的相互作用规律，即库仑定律。定量表达式为：

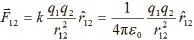
比较万有引力定律与库仑定律，首先表达式非常相似，相互作用力的大小都满足平方反比关系，与点的量的乘积成正比，方向沿联线方向，质点模型和点电荷模型都是当实物的限度与距离相比很小时的理想化；其次，库仑力的大小与电荷移动无关的特性又和万有引力的大小与质点移动无关的特性类似；再次，两个定律都是通过观察和实验总结出来的经验定律，不是什么理论的逻辑结果，但它们分别是整个经典力学理论和经典电磁学理论的基础，有着奠基性的作用；最后，两个定律常数的首次精确测定，都是通过扭秤实验完成的，设备及实验原理也很相似。

物理学史研究表明，库仑定律的发现，很大程度上是受到万有引力定律的启发。1760年，D.伯努利首先猜测到电力会不会也跟万有引力一样，服从平方反比定律？他的想法显然有一定的代表性，因为平方反比定律在牛顿的形而上学自然观中是很自然的观念，如果不是平方反比，牛顿力学的空间概念就要被改写[1]。1775年，英国唯物主义哲学家普瑞斯特列（1733—1804）通过反复观察小软木球在带电金属罐内外不同的受力情况，以类比的思想大胆提出猜想：“难道我们就不可以从这个实验得出结论：电的吸引与万有引力服从同一定律？因为容易证明，假如地球是一个球壳，在壳内的物体受到一边的吸引力，决不会大于另一边的吸引力。”普瑞斯特列本人没有加以证明，但却为后来的物理学家提出一个研究的方向。1785年，法国科学家库仑通过自行设计的“扭秤”实验证实了普瑞斯特列的平方反比的猜想，完成了库仑定律的定量表示式[2]。其中引力与电量成正比的假设纯粹是库仑在同牛顿万有引力定律的类比过程中引入的[3]。

2 描述场的物理量

在牛顿力学中，牛顿把物体之间的万有引力看成是一

种“超距作用”。这虽然是很不自然的，但是由于万有引力理论在天体力学上取得的巨大成功使人们相信，两个不相互接触的点电荷之间的静电力理所当然也是“超距作用”。近代物理学发展证明，“超距作用”观点是错误的。电荷在其周围产生电场，而电场对放入其中的电荷有力的作用。类比电场的概念，万有引力的“超距作用”就不言自明了。

作者：张国前，宁夏师范学院物理与信息技术学院教授，研究方向为物理教学论（756000）。

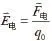
与点电荷的电量成正比，与距离的平方成反比，方向沿径向。这样，在以点电荷为球心的同一球面上各点的电场强度大小相等，满足球对称性。

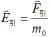
电场满足叠加原理，这是库仑力叠加性的必然结果。从万有引力定律和力的叠加原理出发，同样可推知，引力场也满足叠加原理。

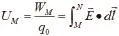
引力场中引入引力势物理量，同样表征引力场的能量特性。与静电场类比推导，引力场中以N点为引力势零点，则M点的引力势为：

对于地球，可看成是质量均匀分布的球体，周围的引力势相当于质量集中到球心的质点产生的引力势。通常选地球表面为零参考点，在地面高度为h的地方，引力势：

3 场遵循的主要规律

高斯定理 静电场遵循高斯定理：通过一个任意闭合曲面的电通量φE等于该面所包围的所有电量的代数和除以ε0。即：

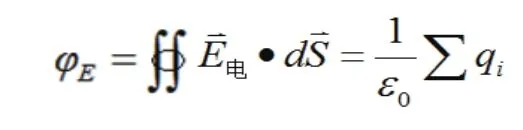
对于连续带电体：

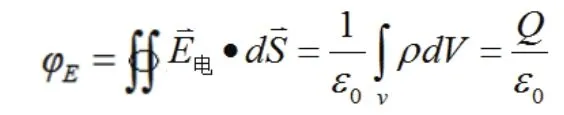
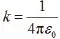
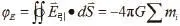
即引力场强在任意闭合曲面上的通量等于该闭合面包围的所有物体的质量和乘以-4πG，与闭合面外的质量无关。

类比于静电场高斯定理的证明方法[4]，引力场强的高斯定理是很容易证明的，故不做详细证明。

4 典型例子——球壳和球体的电场与引力场类比

在静电场中，应用高斯定理能方便求得电荷分布具有一定对称性的带电体产生的电场分布。如对于带电量为Q的均匀带电球壳、均匀带电球体，利用高斯定理可求得它们产生的电场分布情况分别是：

理这个问题，但是只是习惯于用高斯定理解决静电场的问题，从引力场的角度解决问题还不大习惯。当然，可以用积分法做证明，详细的步骤可参考资料[5]。

5 小结

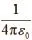
牛顿在发现万有引力定律时曾面临这样一个问题：地球对地面上物体引力的距离为什么要从地心算起？这在牛顿时代是个不小的难题，牛顿自己发明了微积分把它解决了。这里已清楚地证明，从外边看，球对称物体（带电体）产生的引力（电力）作用，就像其质量（电量）集中在球心一样。应用高斯定理，可以用对称的方法非常简捷地处

类比推理对科学的发展起着积极的推动作用。正如麦克斯韦所说：“我认为依靠物理的类比，一门科学的规律与另一门科学的规律之间的部分类似，将使我们能从这两门科学中的一门科学来说明另外的一门科学。”[6]通过万有引力定律与库仑定律的相似之处，由静电场的电场强度、电势概念引入引力场强度和引力势，对引力场从力和能两个方面进行描述，得到引力场类似于负电荷的电场的结论；由静电场的高斯定理、环路定理得到引力场的高斯定理和环路定理，进一步认识了两种场的有源性和无旋性，因此可以利用静电场中已学会的方法去处理引力场的问题，如在求解某些具有对称性的物体与质点的万有引力时，利用引力场的高斯定理能大大简化计算。

[1]郭奕玲.物理学史[M].2版.北京:清华大学出版社, 2005:91.

[2]朱鋐雄.物理学思想概论[M].北京:清华大学出版社, 2009:87.

[3]朱荣华.物理学基本概念的历史发展[M].北京:冶金工业出版社,1987:92.

[4]赵凯华.新概念物理教程电磁学[M].2版.北京:高等教育出版社,2006:23.

[5]赵凯华.新概念物理教程力学[M].2版.北京:高等教育出版社,2004:339.

[6]蔡香民.万有引力与高斯定理:类比在物理学中的应用[J].安徽师范大学学报:自然科学版,2002(2).

Analogical Discussion on Electrostatic Field and Gravitational Field/

/ZHANG Guoqian

Analogy is an important perception method in physics. The basic laws of experiment, the definition of macroscopic characteristic quantities, the substantive description and the expression and application of principal rules are all showed many similarities and different characteristics. The physics concept and its ideas can be comprehended deeply by analogy.

electrostatic fi eld; gravitational fi eld; analogy

G642.423

B

1671-489X(2015)18-0154-03

宁夏2012年高等学校教学质量与教学改革工程项目；宁夏师范学院重点科研项目（ZD2011003）。

10.3969 /j.issn.1671-489X.2015.18.154