A-D检验在取水户水量在线监测数据稳定性分析的应用

蒋吉发，刘 飞

（四川省水文水资源勘测局，四川省成都市 610036）

A-D检验在取水户水量在线监测数据稳定性分析的应用

蒋吉发，刘 飞

（四川省水文水资源勘测局，四川省成都市 610036）

本文引入Anderson-Darling检验方法对国家水资源监控能力建设项目取水户水量在线监测数据的正态性分布特征、置信度进行分析，确认监测数据是否稳定、可靠。

Anderson-Darling检验；水资源；水量监测；正态性

0 引言

为实施最严格水资源管理制度，国家启动了水资源监控能力建设项目，其中最重要的就是对规模以上取用水户的取水量进行在线计量监测，作为对取水户用水量考核和水资源费征收的重要依据[1]。

根据调查，取水户的取水方式既有泵站扬水，又有自流引水；计量设备既有安装在引水管道上的，也有安装在出水管道上的，还有安装在净水构筑物（设备）之间的；有的取水户只安装一个计量装置，有的取水户在不同取水管上分别安装计量装置；有的取水户已装有计量装置，有的取水户没有安装计量装置。有的取水户既有计量装置还因人为调整，数据偏差较大。同时，取水户的取水量根据其供水对象不同，也呈现不同变化规律。供城镇生活用水的取水户白天取水量大、夜晚取水量小，夏季取水量大、冬季取水量小；对于工业企业取水户是随着企业生产情况、生产规律以及设备运转情况变化的。因此，安装的计量设备采集的瞬时流量波动频繁，在不同时段取水量也是不同的。

项目涉及取水户取水量较大，计量管径一般都在300～1000mm，较大的管径达2000mm左右。计量器具虽然在出厂时进行了检定，但受安装现场边界条件限制和安装调试误差影响，计量数据存在一定误差。由于不能影响取水户的生产，也无法拆下计量器具送回专业检测机构进行检测。在项目规划建设时，又没有考虑由国家法定计量检测机构对新安装的计量设备进行现场在线校准检定。因此，如何判定安装的计量装置工作是否稳定、其计量数据是否稳定可靠，是取水户、项目单位、各级水行政主管部门非常关心的问题。如果在同一工况、同一时段内的累计取水量概率分布呈正态性分布，且置信度满足正态性检验要求，即可认为该监测点的数据是稳定可靠的。

1 Anderson-Darling检验

在现有正态性检验方法中，χ2和KS检验最为常用[2]。χ2对样本长度要求较高，通常在N＞200情况下才能获得比较理想的检验效果；在分布参数未知并需要从样本估计的场合，KS检验的精度不高[3-5]。这些缺陷限制了传统分布检验算法在水量监测数据稳定性检验中的应用。

Anderson-Darling检验是正态性检验的一种，能够在较小样本（N＞5）的情况下，对数据拟合度进行分析检验。通过计算样本分布函数（CDF）和经验概率密度函数（EDF）之间的二次A-D距离来衡量样本是否属于某一特定分布族，即判断原假设H0是否成立[6-8]。用F（χ）和Fn（χ）分别表示样本序列CDF和EDF。原假设H0为真，则表示样本χ1，χ2，…，χn同分布，且分布函数为F（χ；θ），θ为分布函数参数向量。

Anderson-Darling距离A2n为：

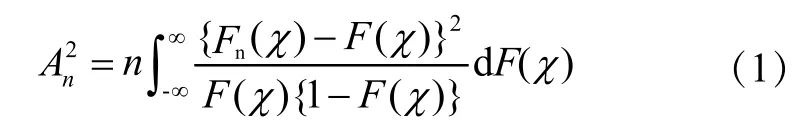
实际工程应用中，常用离散表达式（2）来计算Anderson-Darling距离，式中Zi=F（χi）为概率积分变换（PIT）函数。

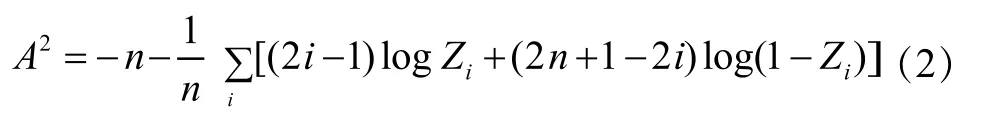
其中，Zi为参考采样xi对应的分布函数值（CDF）。将样本带入式（2）即可得到A-D检验值A2与相应的临界值进行比较，若大于临界值则在置信度水平α下拒绝原假设H0，反之则接受H0。

表1 A-D检验正态性检验临界值

2 取水量A-D检验分析

采用Anderson-Darling检验来分析成都2012年“国控”项目取水户水量监测数据的分布拟合程度，从而分析监测数据的稳定性规律。根据有关技术要求，水资源监控能力流量计计量误差为不大于±5%，因此，利用A-D检验时α=0.05。

2.1 基本情况

四川省成都市2012年度“国控”项目涉及规模以上取用水户31户、74处水量监测点，主要是工业及城镇生活用水。该项目新装流量传感器41处、直接接入既有流量传感器33处。取水户水量在线监测数据通过RTU每隔5min采集一次，再通过GPRS/GSM传输至四川省水资源管理信息中心平台。2014年8月15日～10月30日，共计77天，监测点有效数据70处（其余4处因取水户停产没有采集数据），单点总样本量22176。

通过对样本数据统计分析，受取水方式及取水系统工作运行方式的影响，单点瞬时流量和时段取水量会不断发生变化。一天24h内每小时的取水量会不尽相同，在一年365天中每天的总用水量也不尽相同。

2.2 取水量变化规律分析

2.2.1 日水量变化影响

为了解不同时段的取水水量稳定性，按1h、3h、6h、24h五种时间间隔分析10个监测点水量数据正态性拟合程度，结果见表2。随着对时间间隔的不断增加，取水水量数据的分布程度越拟合于经验函数（CDF）。以5101240005001监测点为例分析的概率拟合度分布见图1。

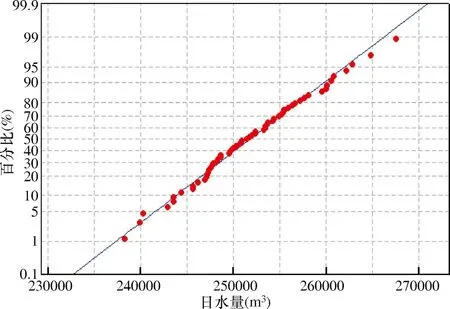
图1 5101240005001监测点监测数据正态性检验拟合分布图

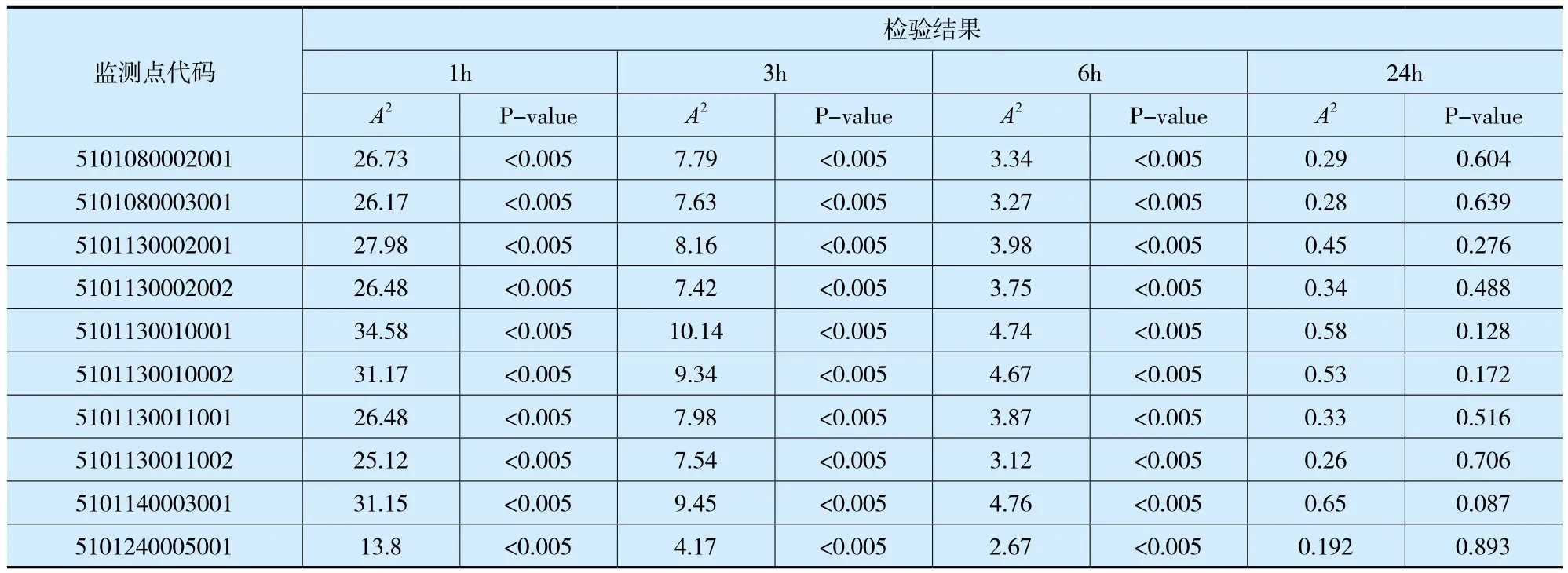
表2 日变化检验分析（N=22176，α=0.05）

2.2.2 取水工况变化分析

根据各取水户取水工况变化，按照日水量时间间隔分析监测站水量数据正态性拟合程度，结果见表3。

取水户取水水量因受供用水需求、取水方式等因素影响，单位时间内的取水量会呈现数据区间离散，但区间内数据又呈现集中的分布情况，即离散—集中分布数据，见图2、图3。对集中的区间数据进行正态性检验发现，区间内数据满足正态性检验。

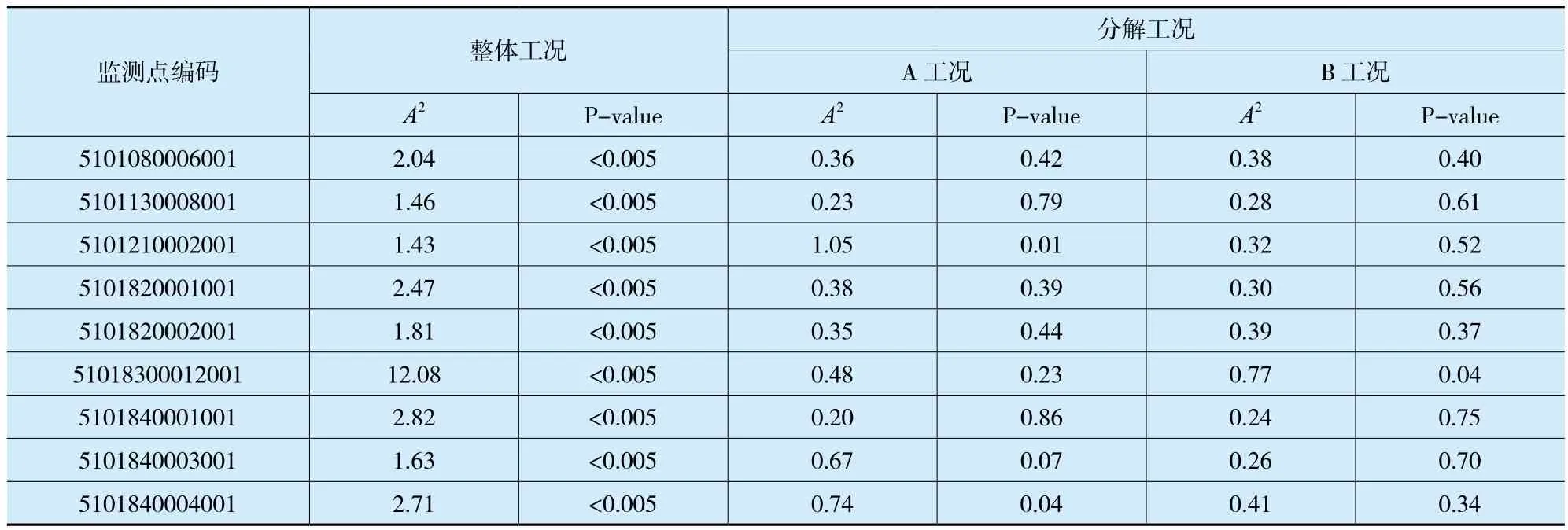
表3 复杂工况下监测数据检验分析（N=22176，α=0.05）

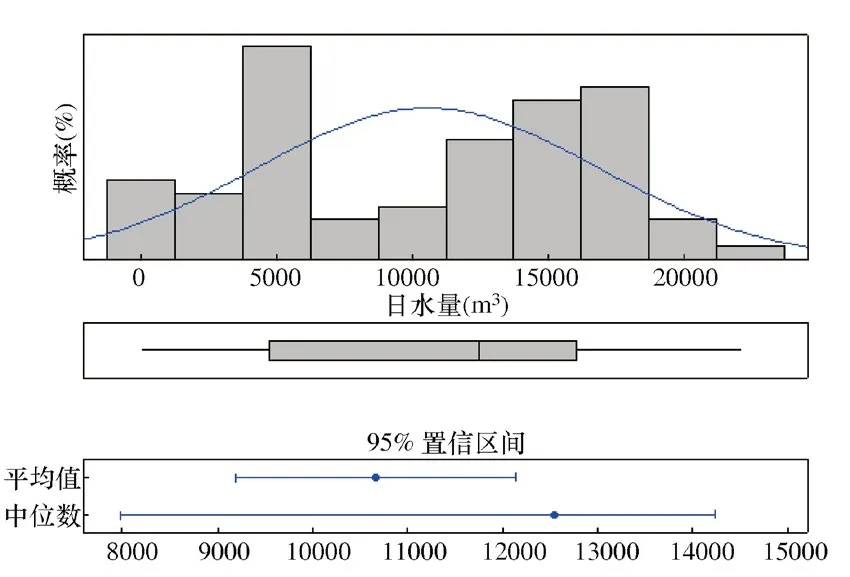
图2 5101080006001 水量（0～30000m3）概率分布立方图

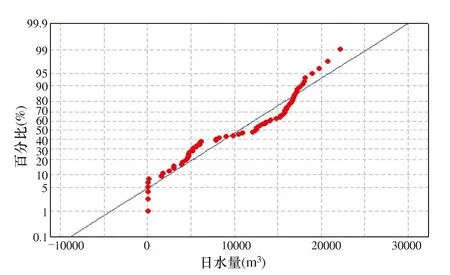
图3 5101080006001 水量（0～30000m3）正态性检验拟合分布图

2.3 检验成果

由于累计取水量计取时段过短（1h、3h、6h），其取水量相对来讲不太稳定，但也不是取水时段越长越好，因为时段加长后可能出现不同的取水工况，其取水量也不稳定。本项目取水量数据按24h为时间间隔，且根据取水户取水工况，进行正态性检验分析。通过对项目70处监测点的分析，34处监测点按整体工况分析通过检验，36处监测点按分解工况分析通过检验，其计量误差满足要求。

3 结论

（1）通过对日水量变化及取水工作方式变化的分析，将Anderson-Darling检验方法引入到水量在线监测数据稳定性分析是可行的。

（2）以24h取水量（时段累计水量）数据为分析样本数据，以取水户不同工况为分析情况，进行数据拟合度的分析，其成果较为可靠，计量误差满足要求。

（3）如果样本系列A-D检验满足正态分布，且置信度达到95%，则可认为其取水量监测数据是稳定的。

[1] 蔡阳.国家水资源监控能力建设项目及其进展[J].水利信息化，2013（6）：5-10.

[2] 王斌会，徐勇勇.正态性检验的图示方法及其应用[J].数理统计与应用概率，1996，（3）：249-256.

[3] 周洪伟.正态性检验的几种常用的方法[J].南京晓庄学院学报，2012，（5）：13-18.

[4] 张维，于盛林，张弓.基于Anderson-Darling检验的恒虚警检测[J].光电工程，2009，（2）：39-44.

蒋吉发（1967—），男，高级工程师，四川省水文水资源勘测局总工程师，长期从事水文水资源管理技术工作。E-mail：776984707@qq.com

刘 飞（1989—），男，助理工程师，主要从事水资源分析评价工作。E-mail：2258430275@qq.com

A-D Detection in the Application of Stability Analysis on On-line Monitoring Data about Lntake Water Amount

JIANG Jifa，LIU Fei
（Hydrology and Water Resources Survey Bureau of Sichuan Province，Chengdu 610036，China）

In the paper，Anderson-Darling detection method is used to analyze normality distribution characteristics and confidence degree of on-line monitoring data about intake water amount in the National Water Resources monitoring capacitybuilding project，in order to confirm whether the monitoring data are stable and reliable.

Anderson-Darling detection；water resources；water amount monitoring；normality distribution characteristics