大型风电机组现场运行数据预处理与模型建立

李大中 许炳坤 常 城

华北电力大学 河北 保定 071003

0 引言

近年来中国风力发电技术与风力发电制造业得到了迅速的发展。为更好的认识和控制风力发电过程，一个准确的机组运行模型是必不可少的。文献［1］建立了风电机组暂态模型并分析研究了系统稳定性和电能质量。文献［2］和文献［3］分别通过simulink模块和数学机理建立风电机组模型并分别提出直接转矩控制方法和模糊控制方法。传统机理模型所设定风轮和发电机的参数较理想化，并且无法考虑风向与机舱夹角与机组输出功率之间关系，因此传统模型难以与风场运行数据相吻合。作为风电机组运行过程最主要影响因素，风速直接决定机组运行工况。风速作为变化量，在时间上具有连续性，而传统评价指标如方差、平均差，不能很好地反映风速波动变化情况，因此需要一种新的评价指标来衡量风速这一类具有连续变化特性变量的波动情况。

本文基于大型风电机组现场运行数据建立的过程模型以及针对连续数据波动变化程度提出的评价指标可以有效弥补传统方法的不足。

1 大型风电机组运行特性分析

1.1 机组的启动

本文所讨论风电机组为大型恒速风力机，切入风速为 3.5m／s，额定风速为 12.5m／s，切出风速为10分钟平均风速25m／s或瞬间风速30m／s。该机组使用异步发电机，额定输出功率1100kW，额定电压690V，额定频率50Hz。

若风场风速连续120s超过额定风速，机组检查偏航制动系统并调整变桨角度至70°，满足上述条件后，机组控制系统根据风速计算设定变桨角度，发电机逐步增速，在转速达到同步转速±6%的范围时，转速变频辅助启励回路启动，调节发电机系统转矩函数数值与系统同期后风机主开关并网，连接到电网上输出电功率。此时启动程序全部完成，风机处于稳定的工作状态。

若风速突然降低致启动过程不能完成，风机终止提升转速。待满足条件后，自动重新进行。

1.2 机组的运行

正常运行中，当风速在额定值以下时，桨距角稳定在最大迎风角-19°附近以获得最大风能，当风速在额定值以上时桨距角自动进行调整，使风机保持额定功率。转速变频辅助启励回路一直处于工作状态，保证发电机转速稳定。

1.3 机组的偏航控制系统

该机组采用自动对风偏航方式，机舱顶部装有风向标，将风向变化用电信号传递到偏航电机控制回路处理器。当检测到偏航误差角度达到设定值±15°以上，控制系统发出指令，偏航刹车解除，机组进行顺时针或逆时针偏航。当机舱方位与风向的偏差达到设定值以内，风向标失去电信号，电机停止工作，偏航刹车制动，偏航结束。

2 风电机组现场数据分析与预处理

该机组现场运行数据包括时间、风速、功率因数、变桨角度、风向角、机舱角、频率、发电机电压和发电机输出功率等机组主要参数以及风机舱内各测点的温度和压力等运行监测参数。

2.1 数据分析理论依据

考虑风力发电过程主要影响因素，风电机组输出有功功率P与风速等参数近似关系式为［2］：

式（1）中：ρ—空气密度；V—风速；A—扫风面积；η1—发电机效率；η2—传动效率；CP—风能利用系数。

风能利用系数是由桨距角β以及叶尖速比λ（风轮叶片的线速度与风速之比）决定［3］。关系式如下［4］：

式（2）中：风机偏航误差角与风向角度存在大小为θ的偏差时，风力发电机获得的风能是风轮正对时（θ=0）的cos3θ倍。此时，风机损失功率所占比为［5］：

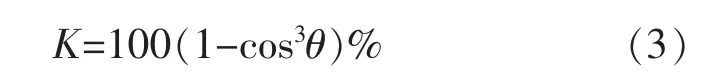
选择风速、变桨角度与偏航误差角度作为机组运行过程的主要影响因素，即模型输入量，建立与输出量发电机输出功率间的过程模型。

2.2 现场数据筛选分析

选取该机组2013年6月25日全天各参数运行数据288组，如图1所示。

图1 机组各参数运行数据

由图1可知，风电机组输出功率变化与风场风速变化趋势基本相同。经计算，输出功率与风速之间复相关系数为0.9533，接近于1，表明两者线性相关程度很高。在风速与功率较低时，叶片多次调节桨距角，增大风轮所受转动力矩；当风速未达到额定风速，变桨角度始终控制在最大迎风角，保证机组在低风速下最大程度吸收风能，此时变桨距风机可认为等同于定桨距风机［6］；当风速超过额定风速，机组通过调节桨距角来改变气流对叶片的攻角，进而改变叶片所受空气转动力矩，保证机组输出功率稳定。偏航系统通过调整机舱角，保证机组最大程度吸收利用风能，同时避免由于斜向入流引起的附加负载［7］。当风速平稳时，机组偏航误差较小；当风速波动较大时，机组偏航误差明显增大，表明此时风场风速风向变化较快，不利于风电机组吸收风能。

2.3 现场数据的预处理

在机组故障、人为因素、以及风力场异常等情况下，机组运行数据有时不能真实有效地反映机组运行状态和输入与输出参量之间的关系。因此，本文提出一种对现场数据的预处理原则，即对以下三种情况的数据予以剔除：

1）风速未达到切入风速，机组输出功率为零。

2）风速达到切出风速，风轮刹车，机组停机。

3）机组发生故障或人为控制干预等情况下，机组停机。

同时，选取机组连续正常运行数据作为模型训练样本数据，以便真实体现机组运行特性以及输入输出之间关系。

通过对该风电机组全年数据筛选，选取该机组2013年6月中连续24小时以上正常发电运行数据5165组作为建模实验数据。

2.4 风速量波动评价指标建立

作为风力发电过程的关键影响因素，即风速直接决定了机组的运行状态和输出功率。例如，当风速未达到额定风速，机组输出功率处于额定功率以下，桨距角始终稳定在最大迎风角；当风速达到额定风速，机组输出功率达到额定功率，此时桨距角随风速变化而变化，以此来稳定风轮所受转动力矩，进而稳定输出功率。风速波动越小、变化越平稳则越有利于机组的稳定运行。

风速是一个时间连续的变量，评价风速波动变化程度的大小，应当由风速变化量与风速的比较而得。传统评价指标，如方差、平均差等，只适用于表示离散数据中各个数据点与数学期望或算术平均值之间的偏离程度。

基于此本文提出一种连续数据平均相对变化量评价指标，对风速变量的波动程度进行评价，如式（4）所示：

相对于方差和平均差，该指标能够更好地反映连续数据的波动变化程度。选取某风电场机组运行数据进行验证，结果如图2及表1所示。

图2 风速数据样本

表1 各样本对应的评价指标

由图2中各风速样本数据可知，样本1风速基本处于6m／s到9m／s之间，风速曲线呈剧烈波动；样本2风速处于上升过程，样本3风速分为3个相对平稳阶段，其中样本2、3风速波动程度明显小于样本1。

由表1可知，样本1的方差和平均差均小于样本2和样本3，说明方差和平均差只能反映连续数据在采样点上的离散程度，不能反映连续数据的波动性。而样本1平均相对变化量为12.9113%，均大于样本2和样本3，从而表明本文提出的新评价指标能够真实有效的反映实际风速量的动态变化特性。

3 模型建立

3.1 模型构建

以风电机组现场运行数据中风速W、变桨角度T和偏航误差角度E作为模型输入，以风电机组的输出功率P作为模型输出。本文取该机组2013年6月除27日以外实验数据作为训练数据。

图3 风电机组运行过程支持向量机模型

本文采用最小二乘支持向量机建立机组运行过程模型，如式（5）所示［8］：

式（5）中：l—训练次数，K（xi，xj）—核函数，b—偏差。本文采用高斯径向基核函数（RBF）。

3.2 模型验证与结果分析

利用遗传算法对模型参数C和σ2寻优，选择初始种群规模为50，遗传代数为100，参数寻优范围为 C∈［1，10000］，σ2∈［0.1，10］，寻优结果为 C=6010.4，σ2=0.16。

根据寻优得到的C和σ2对LS-SVM模型进行训练，从而确定该风电机组运行过程的最优LS-SVM模型。通过对运行数据的学习训练分别得到支持向量a与偏差b，支持向量a维数与模型学习训练样本组数相同，由于维数过高，在此不便列出。偏差b=0.2569。

为验证模型准确性，选取该机组2013年6月27日全天运行数据作为测试样本，比较模型预测功率与机组实际功率，如图4～5所示。

图4 机组实际输出功率

图5 模型预测输出功率

在模型训练基础上，利用现场数据测试模型泛化能力。取该机组在2013年7月至12月，每月任一天连续24小时正常运行数据作为测试样本，以平均相对误差作为评价指标［9］，并计算各日期风速数据的平均相对变化量，结果如表1所示。

由表2看出，针对该机组其他月份正常运行数据，模型平均相对误差值较小，具有良好的泛化能力。在夏秋季节，由于风场不稳，风速波动程度大，机组运行长期处于动态过程，模型预测误差较大，并由于风速较低时机组输出功率随之下降，导致相对误差增加。在冬季，风场稳定，风速波动程度小，机组能够长期处于稳定运行状态，模型误差小，其中2013年12月22日，风速始终在额定风速以上，机组输出功率维持在额定功率，该样本平均相对误差仅为0.526%。由以上分析可知，本文建立的风电机组LS-SVM模型，风速波动程度越小，模型精度越高。该模型能够较好的跟踪机组实际功率的变化，具有满意的拟合效果和泛化能力。

4 结束语

1）风电机组现场运行数据预处理方法符合理论分析与现场实际情况，根据该方法筛选得到的现场运行数据可以真实有效地反映风电机组运行特性以及机组输出功率与风速等影响因素之间关系。

2）连续数据平均相对变化量评价指标，能够真实有效地反映诸如风速量等现场连续变化量的波动程度。

3）在数据预处理基础上，建立了大型风电机组运行过程LS-SVM模型。验证结果表明，该模型误差与风速平均相对变化量有直接关系，动态过程模型误差大于稳态过程模型。风速波动程度越小，模型精度越高，总体平均平均相对误差为8.424%，说明该模型能够较好的跟踪机组实际功率的变化。

表2 模型预测功率与机组实际功率平均相对误差

［1］徐寅，陈颖，风力发电机组暂态仿真模型［J］.电力系统自动化，2011，（5）：100－107.

［2］刘畅，双馈式变速恒频风力发电机控制方法改进研究［D］.保定：华北电力大学，2010.

［3］王伟娜，基于实测风功率曲线的风机控制方法研究［D］.北京：北京交通大学，2012.

［4］ Whei－Min Lin，Chih－Ming Hong.A New Elman Neural Network－Based Control Algorithm for Adjustable－Pitch Variable－Speed Wind－Energy Conversion Systems［C］.IEEE TRANSACTIONS ON POWER ELECTRONICS，2011，26（2）：473－481.

［5］ 牛山泉 D.风能技术［M］.北京：科学出版社，2009.

［6］陈清丽，风力发电机组风轮建模及运行特性研究［D］.保定：华北电力大学，2007.

［7］张志英，赵萍等，风能与风力发电技术［M］.北京：化学工业出版社，2010.

［8］李大中，李晓江.木屑、稻壳和煤混合型煤压缩成型成型过程建模与工况优化［J］，农业机械学报，2012，（4）：83－87.

［9］孟岩峰，胡书举，邓雅，许洪华.风电功率预测误差分析及预测误差评价方法［J］.电力建设，2013，（7）：6－9.