基于VSC-HVDC风电并网系统风电场侧故障下系统低电压穿越能力研究

边晓燕，王本利，王 靖，杨立宁

（1.上海电力学院，上海 200090；2.上海东海风力发电有限公司，上海 200090）

在全球资源日趋紧张的今天，许多国家把发展风电事业作为缓解能源紧张的一项重要手段。近几年来，无论是风电场规模还是装机容量，都取得了快速的发展。大规模风电场并网运行在缓解电网运行负担的同时，也给电网的安全稳定运行带来不可忽视的影响，因此研究风电场并网运行的安全稳定对于风电场自身和电网的安全稳定具有重要意义。风电场经柔性直流输电（VSCHVDC）并网方式，因是有功无功功率独立控制、可接于无源网络、具有黑启动及潮流反转等优点，一经出现便被认为是一种理想的风电场并网方式。随着风电比重的快速增加，电网对风电机组及其并网系统的低电压穿越能力提出了更高的要求，尤其是双馈风力发电机组因其变流器容量小，所以它对电网电压扰动的抵御能力较弱，因而成为最难实现低电压穿越的机型之一。双馈风力发电机组经VSC-HVDC并网的低电压穿越（LVRT）问题，成为众多学者研究的重点。

文献［1］对于交流电网发生故障扰动的情况，提出了一种基于风电机组惯性支持的故障穿越方法。根据VSC-HVDC直流电压的波动量，调节风电场出口频率，使风机输入的机械功率暂时以发电机转子动能的形式储存，从而减少了风电场输出的电磁功率，提高了系统的故障穿越能力。文献［2-3］通过HVDC两端变流站提供无功支持，并采用基于电压控制的快速功率降低算法控制风电场馈入功率，维持直流系统功率平衡；对风电机组功率控制进行改进，提出分层控制与HVDC控制相协调，保持风电机组的电压稳定。

这些文献仅仅研究了电网侧故障时系统的故障穿越能力，并非是风电机组的低电压穿越能力，由于VSC-HVDC具有隔离故障的能力，电网侧电压跌落对风电场侧的电压影响很小，电网电压的降落并不能直接反映在风机的机端电压上，因此风电场不会受到低电压的威胁。本文将针对风电场侧故障，风电机组的低电压穿越能力进行研究，协调双馈风力发电机组（DFIG）和 VSCHVDC风电场侧变流器（WFSVSC）两个无功源，其目的在于充分发掘风机自身的无功潜能，并结合VSC-HVDC并网这一理想的并网方式，在发生严重故障时，共同对系统进行无功支持，提高风电场的低电压穿越能力。

1 风电场经VSC-HVDC并网系统模型

风电场经VSC-HVDC并网系统结构图如图1所示。风电场由DFIG组成，电网由无穷大系统代替。

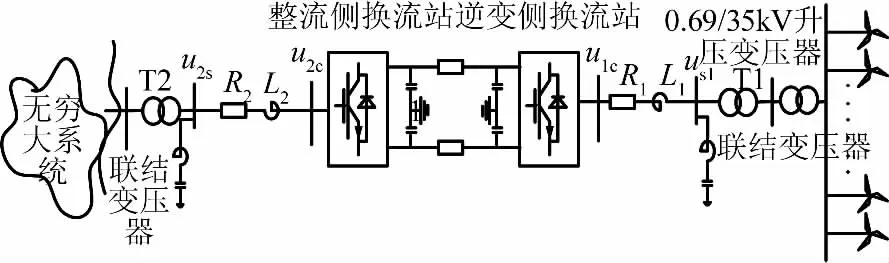
图1 风电场经VSC-HVDC并网系统

1.1 DFlG模型

关于DFIG的数学模型，已有很多文献对这方面进行了描述。DFIG的物理模型［4-6］见图2。

dq轴坐标系中的DFIG的电压方程为：

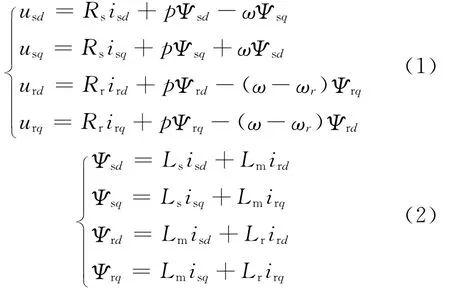
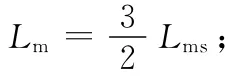
Ls——dq坐标系中定子等效自感，Ls=Lm+Lls；Lr——dq坐标系中转子等效两绕组自感，Lr=Lm+Llr。

电磁转矩表达式为：

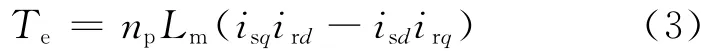
式中Te——电机的电磁转矩；np——电机的极对数。

运动方程为：

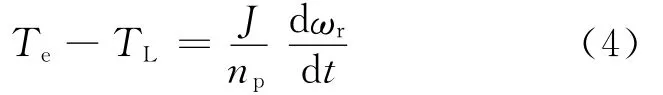
式中TL——风机的驱动转矩；J——转动惯量。

式（1）至式（4）完整地组成了风机的dq坐标系下DFIG的数学模型。

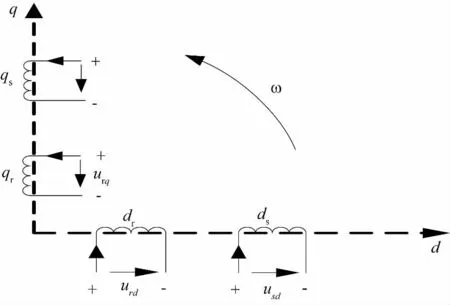
图2 dq坐标系中的DFIG物理模型

1.2 VSC-HVDC 的数学模型

VSC-HVDC和DFIG结构上有相似之处，都含有交—直—交的电压源变流器。因此关于VSC-HVDC两侧换流站及其控制方式的建模可借鉴DFIG的变流器及其控制方式的建模过程。本节首先在dq同步旋转坐标系下建立VSCHVDC的稳态数学模型，针对风电场侧和电网侧的控制目标提出两侧换流站的控制策略。同时利用前馈补偿环节消除变流器d轴和q轴的耦合，实现系统有功功率和无功功率的解耦。

VSC-HVDC的基本结构如图1所示，其中右侧换流站为整流侧换流站，左侧换流站为逆变侧换流站。T1、T2分别表示两侧换流站内的联结变压器，us1、us2表示交流系统的母线电压，uc1、uc2表示换流站输出电压基波分量。R1、R2及L1、L2表示线路的电阻和电感。VSC-HVDC的交流电压和电流通过Park变化转换为dq同步坐标系下的方程为：

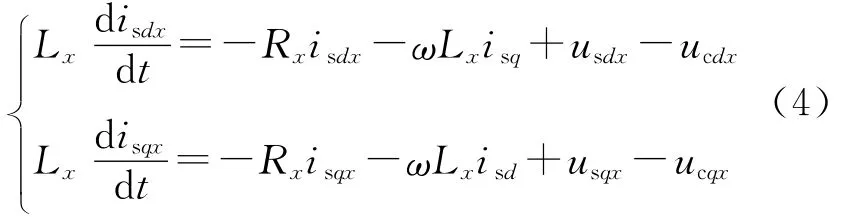
式中 下标x——换流站标号（x=1、2）。

换流器输出电压基波在d轴与q轴分量与直流电压的关系为：

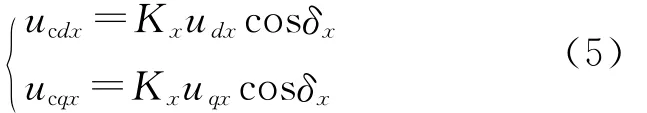
式中 Kx——直流电压利用系数；δx——换流站输出电压与系统电压的相角；Kx，δx都是可控量。

通过改变Kx和δx值，调节换流站输出的电压幅值和相位值。本文采用交流系统电压基波定向矢量控制，即usqx=0，将式（5）代入式（4）得

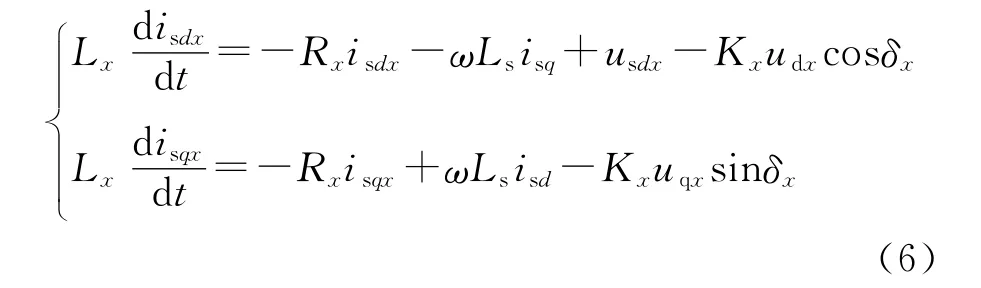
以上是VSC-HVDC的交流侧状态方程，由式（6）可知两端的换流站在d轴和q轴不完全解耦，同双馈风机的变流器相同。而对与VSCHVDC的两端换流站直流侧而言又是关联和耦合的。由图1可知VSC-HVDC的直流侧方程为：

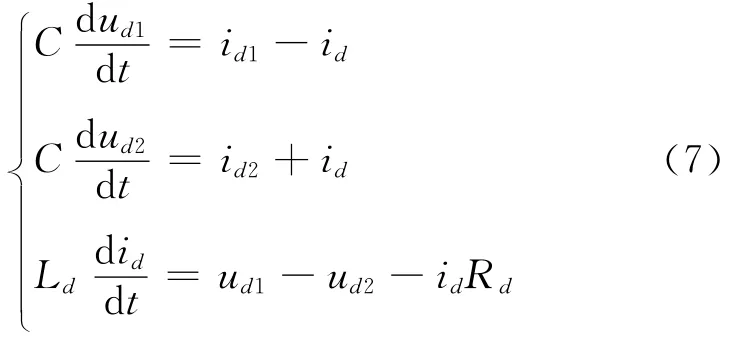
式中 idx——换流站输出的基波电流值；id——直流线路的电流。

式（7）经dq变换，可得

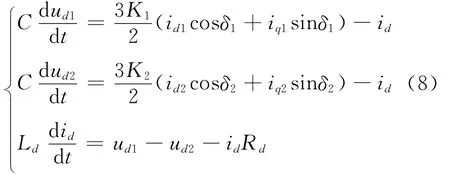
联立式（6）和式（8），可得dq坐标系下7阶7状态变量的常系数微分方程组成的VSC-HVDC数学模型。

采用交流系统电压基波定向矢量控制方式dq坐标下的功率方程为：

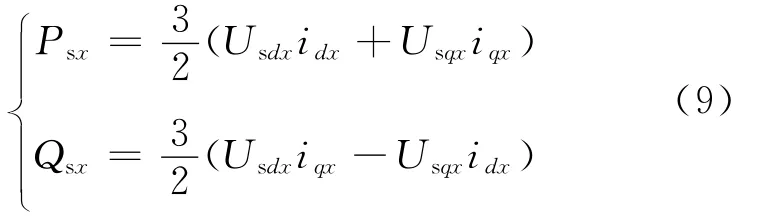
2 DFlG与VSC-HVDC协调控制策略

本文针对风电场侧故障时DFIG的低电压穿越能力进行研究，提出了DFIG与VSC-HVDC协调控制策略，充分利用风机自身的无功能力，同时结合VSC-HVDC风电场侧变流器，共同对故障处提供无功支持。具体控制框图如图3所示。

图3中，上层为DFIG网侧变流器控制，采用定直流电压、定交流电压的控制方式，下层为VSC-HVDC风电场侧变流器控制，采用定无功功率、定直流电压的控制方式，二者通过一个V control的模块连接。V control的作用是通过监测故障处电压落差，计算出所需的无功缺额，然后依次分配给GSC和WFSVSC变流器。

风电场侧母线故障时，风电场和VSC-HVDC变流器都会对其进行无功支持，但是如果不协调好这两个无功源，必定会对母线电压造成冲击，出现电压波动过大等现象。本文通过增加一个V control模块，对这两个无功源进行协调，当风电场侧发生故障时，共同对其进行无功支持。由于DFIG自身发出无功能力有限，当无功需求超过机组无功极限时，需要减少有功出力，以扩大机组无功极限，不利于风机的经济性，相比较VSCHVDC的变流器容量大，可起到STATCOM的作用，动态地对系统进行无功支持，因此，本文优先利用VSC-HVDC风电场侧变流器，在其补偿无功后，系统还有无功缺额时，再充分利用DFIG机组自身的无功补偿能力。这样既保证了风机的安全，又最大可能地利用了风能，兼顾了经济性。同时避免了各个变流器的频繁切换，有利于电压的恢复。其无功控制流程图如图4所示。

VSC-HVDC网侧变流器GSVSC的控制本文以直流电压和无功功率为目标，其控制图如图5所示［12］。

3 风电场等值模型下的仿真验证

3.1 风电场等效仿真模型参数说明

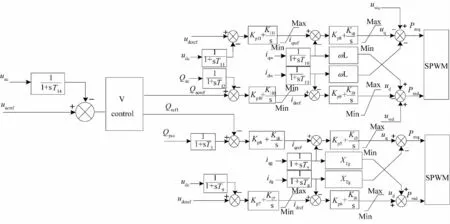
图3 DFIG与VSC-HVDC协调控制框图

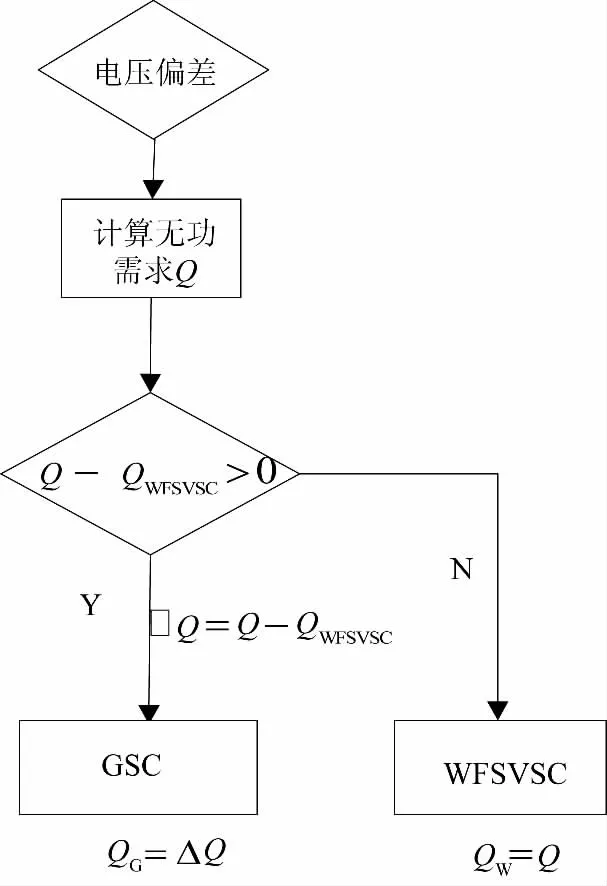
图4 无功控制流程图

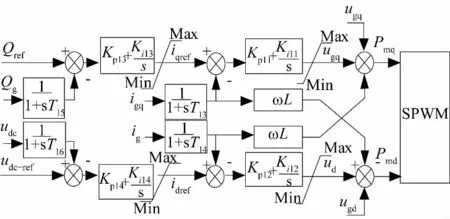
图5 VSC-HVDC的GSVSC控制图

为了验证所提方法的有效性，搭建了如图1所示的仿真模型，其中风电场采用20台并联风机组成的等效风力发电系统，每台风机额定容量为5MW，单机网侧变流器容量为2MW，经电抗器接入三绕组变压器，三绕组变压器高中低电压分别为30、3.3、0.69kV。单台DFIG风机及网侧变流器的参数如表1所示。

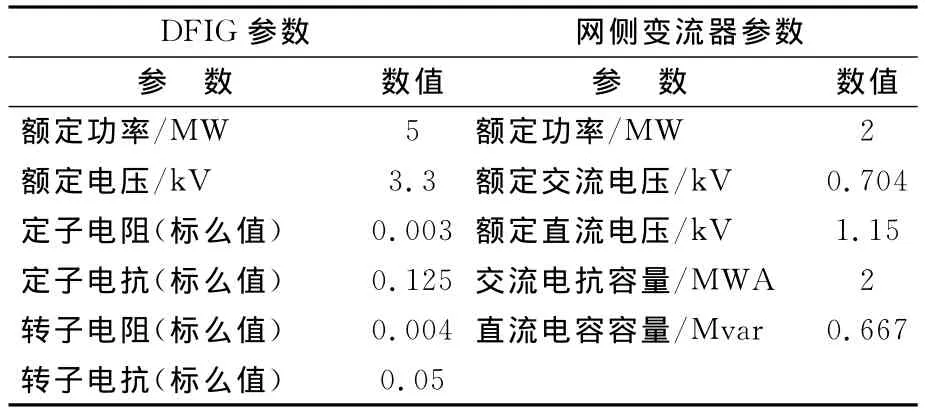
表1 单台DFlG风机及其网侧变流器参数

3.2 算例仿真

如设置在1s时的风电场并网点PCC母线发生非金属性三相短路接地故障，其中短路阻抗为6+j6Ω，电压跌落至约20%，故障持续150ms后清除。电网电压标幺值由1.0跌落到0.2。仿真波形如图6所示。

由图6（a）可以看出，故障清除后采用协调策略的PCC点电压在1.5s达到稳态，而不采用协调策略的PCC点电压在2.5s左右达到稳态，并且不采用协调控制的电压标幺值振荡幅度达到1.15，高于采用协调控制的电压标幺值振荡幅度1.02。由图6（b）、（c）可以看出，当故障较大时，撬棒保护（Crowbar）动作，风机变成异步机需要吸收无功，并且采取协调控制策略时风机吸收的无功要比无协调控制时小。由图（d）看出，采取协调控制策略DFIG输出的有功功率波动要小于无协调控制策略。

由仿真算例可以看出，采用协调控制能加快故障恢复时间，减小震荡幅度，具有更好的低电压穿越能力，且风机输出的有功功率波动更小。

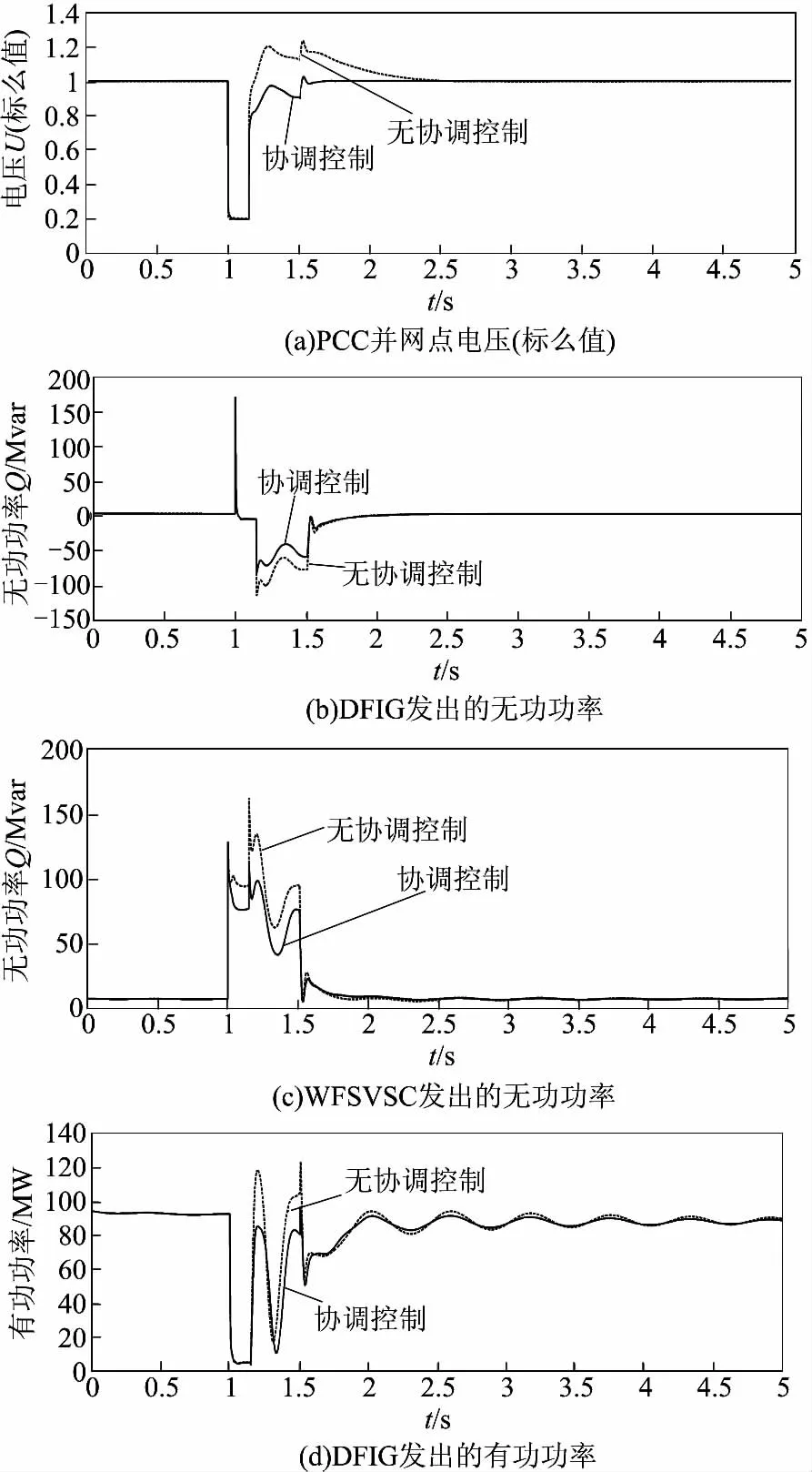
图6 风电场侧非金属性三相短路故障（电压跌落至约20%）

4 结论

本文建立了风电场经VSC-HVDC并网方式的数学模型，针对VSC-HVDC风电场侧故障，提出了协调控制策略，通过原理分析与仿真，得到如下结论。

（1）风电场侧故障，造成PCC点电压降低，DFIG和WFSVSC都对PCC点电压进行控制，易造成故障清除后该点电压波动过大，不利于电压的恢复。

（2）提出了 WFSVSC和DFIG的GSVSC的协调控制策略，能够优化对PCC点的无功控制，并与无协调控制进行了对比，可以得出采用协调控制策略能充分协调DFIG和VSC-HVDC变流器向电压跌落点提供无功支持，有效减小故障恢复时期的电压波动和风机输出的有功功率波动，加速故障恢复时间，具有更好的低电压穿越能力。

（3）采用有功无功控制策略不需要额外增加设备，只需要对DFIG和VSC-HVDC的控制策略进行修改，便能取得较好的效果，具有很高的性价比。

［1］ 王毅，付媛，苏小晴，等.基于VSC-HVDC联网的风电场故障穿越控制策略研究［J］.电工技术学报，2013（12）：150-159.WANG Yi，FU Yuan，SU Xiao-qing，et al.Fault ridethrough control strategy of wind farmintegrated with vschvdc［J］.Transactions of China Electrotechnical Society，2013（12）：150-159.

［2］ 章心因，胡敏强，吴在军，等.基于VSC-HVDC的风力发电系统低电压穿越协调控制［J］.电力自动化设备，2014（3）：138-143.ZHANG Xin-yin，HU Min-qiang，WU Zai-jun，et al.Coordinated lvrt control of wind power generation system based on vsc-hvdc［J］.Electric Power Automation Equipment，2014（3）：138-143.

［3］ 章心因，胡敏强，吴在军，等.基于VSC-HVDC并网风电场的低电压穿越技术研究［J］.电力系统保护与控制，2014（19）：93-99.ZHANG Xin-yin，HU Min-qiang，WU Zai-jun，et al.Research on the low voltage ride-through technology of integrated wind farms based on VSC-HVDC［J］.Power System Protection and Control，2014（19）：93-99.

［4］ 廖勇，王国栋.双馈风电场的柔性高压直流输电系统控制［J］.中国电机工程学报，2012，32（28）：7-15 LIAO Yong，WANG Guo-dong.VSC-HVDC System Control for Grid-connection of DIFG Wind Farms［J］.Proceedings of the CSEE，2012，32（28）：7-15.

［5］ 霍淑珍，张雷.双馈感应发电机风电机组的动态模型构建［J］.电力与能源，2013（4）：393-397.HUO Shu-zhen，ZHANG Lei.Doubly fed Induction Generator Wind Turbine Dynamic Model［J］.Power ＆ Energy，2013（4）：393-397.

［6］ 陈澜，杨苹，周少雄，等.电网电压跌落对海上风电系统无功补偿的影响分析［J］.电力与能源，2014（4）：521-524+532.CHEN Lan，YANG Ping，ZHOU Shao-xiong，et al.Influence of Grid Voltage Drop on the Reactive Power Compensation of Offshore Wind Farms［J］.Power ＆ Energy，2014（4）：521-524+532.