立方体外壳片段算法在财务数据仓库中的应用

张治坤， 吴小朋， 邢承杰， 邓昌明， 袁 玲， 姜 宁

（北京大学计算中心，北京 100871）

0 引 言

数据仓库系统又称作联机分析处理（OLAP）系统［1］，它以面向主题的方式集成多个异构数据源的数据，为快速决策分析提供支持．数据仓库通常使用多维数据结构进行建模，每个维对应于模式中的一个或多个属性，每个单元存放某种层次的聚集度量值．数据仓库的实际物理结构可能是关系数据库或多维数据立方体，但在逻辑上我们可以将它们都看成多维数据立方体，这样便于观察和分析．数据立方体全部或部分预计算可以大幅提高联机分析处理的性能，这也正是数据仓库优于传统的事务数据库系统的一个重要方面．

数据立方体预计算也称作物化，是数据仓库实现的一项基本任务．物化算法的优劣直接影响联机分析处理的效率．物化方法有完全物化和部分物化两大类，完全物化即计算整个数据立方体的方体格［3］，这需要海量的存储空间来存放预计算的方体，同时预计算的时间也会相当漫长．完全物化对应于完全立方体算法．部分物化［2］分为两种情况，一种是只计算数据立方体的一个子集，使得它只包含满足用户指定的某种标准的单元（如度量值大于某个阈值），但这种方法仍然可能计算方体格中的所有方体，只是某些方体可能计算不完全．冰山立方体算法就是这种部分物化算法的典型代表［4－6］．另一种部分物化方法则是有选择地计算方体格中所有方体的一个子集，而对于选中的每个方体都完整地进行计算．立方体外壳算法［3］和立方体外壳片段算法［7］都属于这种类型．立方体外壳片段算法在处理高维数据立方体的预计算上具有较大优势，在预计算时间、占用存储空间和联机分析处理性能等各个方面能取得较好的平衡．

1 高校财务数据仓库

高校财务数据涉及科研、教学、行政等各个领域，内容纷繁复杂．我们首先设计整个财务数据仓库的模型结构，然后选择财务数据的子集科研财务数据作为我们实验的基础数据，并由此构建财务数据仓库．另外，由于在科研财务数据中提取的维度只是财务数据中维度的一个子集，所以整个的财务数据仓库是一个更为典型的高维数据仓库．

当前最流行的数据仓库的数据模型是多维模型，细分下来，多维模型包括星形模型、雪花形模型和事实星座模型等形式［3］．事实星座模型也称作星系模型，它可以看成多个星形模型的汇集．这种模型一般适合于复杂的数据仓库系统，需要多个事实表来描述我们需要的数据，这些事实表可能有自己特有的一些维表，也可能共享一些维表．

由于高校财务数据中科研、教学和行政相关子系统数据结构并不一致，因此需要用不同的事实表来进行描述．首先选定事实表，在财务数据仓库中，关注科研、教学和行政等方面的财务数据，因此需要这几个方面的财务明细事实表．然后提取三个事实表共享的维表，这样的维表包括时间维、部门维和会计科目维等．还可能存在某些事实表之间共享而另一些事实表不共享的维表，如科研财务事实表和教学财务事实表共享题目维，而行政财务事实表并不需要这样的一个维．最后需要提取各事实表自己特有的维，如科研财务事实表特有的维有项目级别、项目研究类别和批准部门等维．图1为基于事实星座模型建模的财务数据仓库科研子模型［11］．

图1 科研财务数据仓库星形模型

2 立方体外壳片段算法

2．1 立方体外壳算法

2．2 立方体外壳片段算法

立方体外壳片段算法［7］考虑到数据仓库中并不是所有维的组合都会经常在OLAP操作中被涉及到，因此预计算整个立方体外壳是没有必要的．另外，立方体外壳算法无法支持维度高于立方体外壳厚度的OLAP操作，这就意味着用户的高维OLAP需求将很难得到满足．立方体外壳片段算法创造性地将信息提取领域内广泛使用的倒排索引数据结构引入到数据立方体预计算领域中来，通过在倒排索引中使用集合的交运算使得我们可以用多个低维的OLAP查询结果合并得到高维OLAP的查询结果．

立方体外壳片段预计算的算法的流程是首先根据领域内知识将财务数据仓库中包含的所有维划分成等长、不相交的外壳片段，然后为每一个1－D方体构造倒排索引，最后在倒排索引中使用集合的交运算将低维的倒排索引集合得到高维方体的倒排索引．

进行这样的改进后，立方体外壳片段算法需要预计算的方体就进一步减少了．还是以财务数据仓库为例，若采用六个大小为3的外壳片段，则只需计算50个方体（考虑了时间维的概念分层）．另外，立方体外壳算法不能适应高维OLAP操作，而立方体外壳片段算法采用了倒排索引结构，首先将高维的OLAP操作分解为多个低维OLAP操作，然后通过倒排索引中使用集合的交运算将结果合并，这样就能支持任意维的OLAP了．立方体外壳片段算法在各种算法中需要预计算的方体最少，且没有任何精度上的损失，同时还可以处理高维OLAP操作，是数据立方体预计算的理想算法．

3 立方体外壳片段的设计

根据前述科研财务数据仓库的描述，从原异构财务数据库中共提取了十八个维．首先是时间维（time），考虑到时间有年、月、日的概念分层，而我们的联机分析处理过程中有很大可能要对这样的概念分层进行查询，我们在后续的处理过程中需要对时间维按年和按月进行汇总，所以时间维实际上相当于三个维．然后从财务明细账目信息中提取项目编号（xmbh）、财务记账编号（cwjzbh）、决算科目编码（jskmbm）、决算科目名称（jskmmc）、凭单号（pdh）、笔号（bh）、部门（bm）、科目（km）、项（x）和题目（tm）等十个维．最后我们从科研项目信息表中提取任务来源代码（rwlydm）、项目名称（xmmc）、负责人职工号（fzrzgh）、负责人姓名（fzrxm）、项目级别（xmjb）、项目研究类别（xmyjlb）和批准部门（pzbm）等七个维．根据领域知识，我们知道我们需要的度量值是金额，所以我们从财务明细账表中提取借方金额和贷方金额两个度量值．

一些研究［7，10］指出外壳片段大小在2到4之间的时候，可以在存储空间和OLAP查询处理效率之间取得平衡．因此为财务数据仓库设计长度为3的外壳片段，并根据领域内知识将各维划分进不同的外壳片段中．比如，在财务数据仓库中，一个很常见的查询类型是查询某部门某个会计科目在一个时间范围内的财务状况，因此将时间维、部门维和科目维划分到一个外壳片段中．表1显示了根据立方体外壳片段算法设计的外壳片段以及各外壳片段需要计算的倒排索引数．注意第一个外壳片段由于时间维上有概念分层，需要计算的倒排索引数和其他外壳片段不同．

表1 立方体外壳片段算法的外壳片段设计

4 外壳片段的预计算

倒排索引是信息检索系统中使用很广泛的数据结构，通过它可以很快速地由元组内的值找到包含该值的元组．在原始的财务数据库中，通过对财务明细表的扫描查找符合我们要求的元组．但若使用倒排索引，则是通过各维的值去查找对应的元组．由于事实表包含大量事实，它的元组数目通常比维表中的元组数目要多很多，这样倒排索引进行查询的效率就比直接查询要高．下面以财务数据仓库中的一个子集作为例子来说明倒排索引的结构．

表2 财务数据仓库事实表（部分）

表2是财务数据仓库中的部分数据，我们选取了7个元组和4个维．其中时间维只使用年份，而决算科目编码维、决算科目名称维和负责人姓名维使用相应维表中的编号表示．以表2中数据为基础，分别构造4个维的1－D倒排索引，表3为时间维1－D倒排索引示例．

表3 时间维1－D倒排索引

有了1－D倒排索引后，可以根据外壳片段的设计选取构造的高维倒排索引，这个过程是通过在倒排索引中使用集合的交运算实现的．从表2中可以看到这里的4个维中只有决算科目编码维和决算科目名称维在一个外壳片段中，因此为它们构造一个2－D的倒排索引（表4）．

在这个例子中，使用立方体外壳片段算法和表2中所示的外壳片段设计，只需要计算这一个2－D倒排索引．对于真实的财务数据仓库，我们在构造了2－D倒排索引后，可以用同样的方法继续构造3－D倒排索引．

表4 决算科目编码维、决算科目名称维2－D倒排索引

5 性能分析

从立方体预计算时间、预计算信息占用的存储空间、以及利用预计算信息进行联机分析处理的效率这三个方面进行比较分析．

5．1 预计算时间对比分析

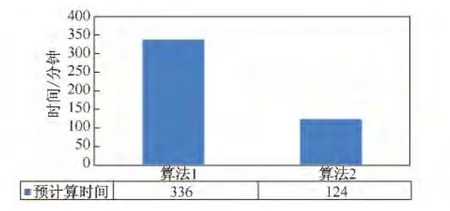
图2 预计算时间对比分析（算法1：立方体外壳算法，算法2：立方体外壳片段算法）

从上图中可以看到，立方体外壳算法需要更多的预计算时间，这是因为它需要计算的方体数目更多．

5．2占用存储空间对比分析

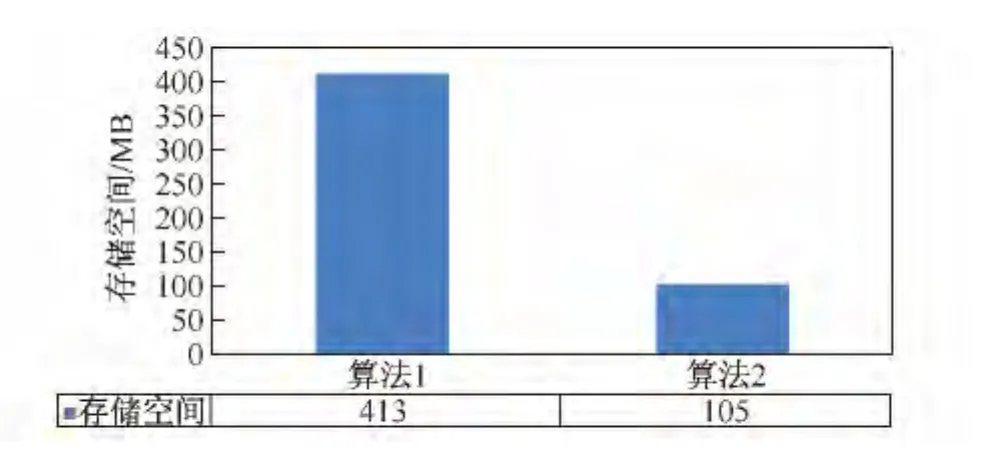
图3 存储空间对比分析（算法1：立方体外壳算法，算法2：立方体外壳片段算法）

两种算法占用的存储空间是和它们需要计算的方体数目成正比的，所以我们有上图所示的结果，立方体外壳算法需要更多的存储空间．

5．3 联机分析处理对比分析

联机分析处理的效率是衡量数据立方体预计算算法的最重要指标，在预计算时间和存储空间可以接受的前提下，联机查询的效率是能被最终用户体验到的最直接的系统性能．

立方体外壳算法只适用于低维情形，更准确地说是只能处理低于外壳厚度的查询，因此对于该算法的性能分析只能在低维情形下进行．对于财务数据仓库，设计的立方体外壳算法采用了厚度为2的外壳，因此采用的实验数据包含18个一维查询和154个二维查询，同时为了降低系统噪声和其他不确定因素的影响，需要把这些查询多运行几遍．

图4 低维联机查询对比分析（算法1：立方体外壳算法，算法2：立方体外壳片段算法）

从实验结果看，立方体外壳算法在低维情形下有效率更高．这是因为该算法预计算了整个立方体外壳，所以能涵盖所有的低维查询情形．看一下两种算法处理一维查询的平均处理时间，立方体外壳算法是13．18毫秒，立方体外壳片段算法是18．74毫秒，虽然两种算法的效率有点差距，但在低维情形下的查询速度都是很快的，在实际系统中完全可以接受．

6 总结和展望

本文首先以异构的财务数据库为基础，设计和构建了科研财务数据仓库．从异构的财务数据库到财务数据仓库，整合了不同历史时期的财务数据，同时，财务数据仓库也是进行数据立方体预计算的基础．

立方体外壳算法仅适用于低维数据情形，而立方体外壳片段算法不仅适用于高维数据情形，在低维数据处理中的预计算时间和存储空间很有优势，虽然在联机分析处理效率上稍有欠缺，但也是可以接受的．今后的工作中将对立方体外壳片段算法进行改进，以提高联机分析处理效率．

［1］ CHAUDHURI S，DAYAL U．An overview of data warehousing and OLAP technology［J］．SIGMOD Record，1997，26：65－74．

［2］ HARINARAYAN V，RAJARAMAN A，ULLMAN J D．Implementing data cubes efficiently［C］／／Proceedings of the ACM SIGMOD Conference．1996：205－216．

［3］ 韩家伟等著，范明等译，数据挖掘：概念与技术［M］．2版．北京：机械工业出版社，2007．

［4］ BEYER K，RAMAKRISHNAN R．Bottom－up computation of sparse and iceberg cubes［C］／／Proceedings of the ACM SIGMOD Conference．1999：359－370．

［5］ HAN J，PEI J，DONG G，et al．Efficient computation of iceberg cubes with complex measures［J］．SIGMOD Record，2001，30（2）：1－12．

［6］ XIN D，HAN J，LI X，et al．Star－cubing：Computing iceberg cubes by top－down and bottom－up integration［C］／／Proceedings of the 29th VLDB Conference，2003．

［7］ LI X L，HAN J W，GONZALEZ H．High－dimensional OLAP：A minimal cubing approach［C］／／Proc．2004 Int．Conf．on Very Large Data Bases（VLDB′04），Toronto，Canada，2004．

［8］ 曹洪岩，陈如亮．校园财务数据仓库系统的建立和OLAP应用［J］．微机发展，2004，14（5）：45－46．

［9］ 赵宝华，阮文惠．高校财务数据仓库系统的设计与实现［J］．计算机工程，2008，34（17）：266－268．

［10］ BERCHTOLD S，BÄOHM C，KEIM D A，et al．Optimal multidimensional query processing using tree striping［C］／／Proceedings of 2nd International Conference on DaWak，2000．

［11］ 张治坤，吴小鹏，邢承杰，等．基于事实星座形模型的财务数据仓库［J］．武汉大学学报：理学版，2012，58（S1）：251－256．