汽车零部件立体仓库货位优化问题研究
2015-12-02祖巧红徐晓霞毛一超
祖巧红, 徐晓霞, 毛一超
(武汉理工大学物流工程学院,湖北 武汉430063)
汽车零部件立体仓库货位优化问题研究
祖巧红, 徐晓霞, 毛一超
(武汉理工大学物流工程学院,湖北 武汉430063)
以立体仓库库存为研究对象,从物流仓储管理角度,研究了货位分配优化问题。分析了汽车零部件货位布局优化原则,建立多目标货位分配优化数学模型,对遗传算法进行了算子设计,运用Matlab软件实现模型的求解,得出可行的货位优化方案。最后结合实例进行多目标货位优化数学模型求解及应用,并以三维仿真图形展示了优化效果,验证了所设计的遗传算法的有效性,对同类问题的解决具有参考意义。
立体仓库;货位优化;遗传算法;Matlab仿真
物流行业的快速发展,对立体库存管理的要求越来越高。制定合适的货位分配策略和良好的仓储布局,不仅可以更好地利用仓库面积和空间,减少库房空间浪费或闲置,还能够有效使用劳动力及设备,物尽其用,提高仓库工作效率,追求运营成本最小化[1]。
以汽车零部件库存为例,其种类繁多,各个供应厂家包装标准不一,各类包装容器的存储方式各异,给仓储作业带来了很大不便。零部件入库作业具有不确定性,出库作业要求更高,呈现明显周期性,为了满足主机厂的高效率出库作业等要求,对零部件货位分配优化问题的研究具有理论和实际意义。
Chan[2]认为,制定合适的仓库存储策略,不仅需要考虑出入库原则,还需要考虑货物尺寸大小、物料处理系统、货位特性、货物需求趋势、周转率和空间需求等因素,这些因素之间是相互联系的。徐骏[3]详细分析了中国市场中汽车零部件企业仓储存在一些的常见问题,并针对先入先出、边角料货物以及货物损坏问题提出了简易快速的解决方案。邵文华和钟绮莎[4]通过现场调研上海大众汽车有限公司的零部件仓库,提出了一种能够有效提升仓库存储空间和货架利用率的方案。Onut等[5]指出货位布局设计的模型一般倾向于优化不同的货位存储目标,比如货位空间利用效率、堆垛机的使用数量、整体设备的使用率等,其最终目的是为了降低仓库年运作成本。Wang等[6]结合遗传算法,将仓库布局成本最小、物料流动成本最小作为优化目标,提出了一种针对不同尺寸大小货物的货位布局优化方法。Zhang[7]结合路径重组(path relinking,PR)和遗传算法,整合交叉和变异算子,旨在解决多目标货位布局优化问题。邹晖华等[8]采用权重法将货位优化的两个目标,即货架货品COI值与货位到出入口时间的积最小和货品的重心最低目标转化为单目标问题,结合遗传算法和Matlab软件环境对模型进行求解。
目前,就货位优化理论的描述文献虽然有很多,但文献大多是基于假设环境进行函数构建和模型求解,由于汽车零部件的种类繁多,标准不一,实际应用中的优化目标也很复杂。因此,在实现过程难度增大,结合实际场景探索成功的案例并不多。本文根据汽车零部件库存调研的库存优化需求,选取多目标优化函数模型,并考虑了各目标权重问题,设计遗传因子,提高遗传算法的效率和实用性,基于Matlab软件进行仿真验证和可视化展示,在货位优化的理论和实践探索上进行了有益的尝试。
1 汽车零部件货位优化目标与假设
本文结合某第三方汽车零部件物流中心实际环境为例研究立体库存优化问题。该物流中心为某整车企业提供不同车型的汽车零部件配送。其库存周转的零部件大小不一,材质各异,总数近2 000种。每种零部件根据其自身特性采用不同的包装形态和堆码方式,按照包装容器分类,一般有台车和料箱两种形式。为了满足不同包装形态零部件的存储需求,自动化立体仓库的货架相应地分为台车货架和料箱货架两种不同类型,本文将选取牛腿式料箱货架作为货位优化对象。
1.1 问题描述
根据零部件分类存储原则,相同的零部件平均分配在每一组货架上,每组货架上所分配的零部件种类和数量相当,因此,只考虑一组货架的货位优化。
每组货架设计为双排、单深式货位,货架区的每条巷道口均设置一个位于仓库的底层的出入库平台,每条巷道都有一个巷道堆垛机,仓库货物同端出入库。每条巷道中托盘尺寸一致,货位的尺寸也一致,货物从货位到出入库口均由巷道堆垛机操作完成,不需要人工干预。每组货架的巷道共涉及MP=2排货架,每排货架共有货位ML=16列,MC=7层,将距出口最近的列记为第1列,货架底层记为第1层,巷道两排货架是对称的,如图1所示。将第x排y列z层的货位坐标记为(x,y,z),( x= 1,2; y=1,2,… ,ML ; z=1,2,… ,MC)。货位三维坐标系示意图如图1所示。

图1 单组货架货位三维坐标系示意图
依次从底层开始对每列货位进行编号,第1层货位编号完毕转向第2层的第1列,依次类推;当第1排的所有货位编号完毕转向第2排的第1层第1列货位,依次类推编号,编号与上一排货位编号连续,不重新从1开始。第1排货位编号如图2所示。

图2 第一排货架货位编号示意图
1.2 确立货位优化目标
仓库货位优化有多种不同形式,本文针对汽车零部件物流需要满足主机厂即时(just in time,JIT)生产需求的特点,将提高仓库货物出入库效率作为主要目标,依据货物周转率和货架的稳定性原则来确立优化目标。
(1) 拣选时间最小:某一货物的库存周转率为某段时间出库总数量与该时间段库存平均数量之比,反映了货物周转的速度[3]。将周转率高的货物储存在离仓库较近的位置,可以有效缩短拣选作业的行进路径及时间,以达到减少拣选作业耗费,并最终实现仓库作业效率地提高。
(2) 货架合成重心最低:货架的承载能力有限,要根据货架实际承受能力合理安排货物存放货位[4]。根据“上轻下重”的原则存储货物,降低货架的合成重心,保证货架的稳定性。
(3) 货架货物重心分布均匀:根据“承重均匀”的原则,将不同重量的货物分配在货架的不同货位,避免将较重货物集中存放在某处造成货架受力不均匀,产生变形或倾覆[8]。
1.3 货位优化基本假设
为了便于货位优化问题模型建立和求解,做出如下基本假设:
(1) 货位上存放的零部件质量分布均匀。在几何意义上,形心是针对抽象几何体而言的,一个面的形心就是截面图形的几何中心,质心则是针对实物体。对于密度均匀的实物体,质心和形心是重合的。如果零部件质量是均匀分布,就能保证零部件存放至货位时,其重心与货位的形心是重合的,便于模型计算。
(2) 巷道堆垛机拣选作业匀速运动。实际应用中,巷道堆垛机的出入库作业在启动和制动过程中存在一个加、减速阶段。通常堆垛机一次运行过程需要经历启动加速、匀速运行和减速制动3个过程。本文在建模过程中,将这个加速和减速时间忽略不计,假设堆垛机一直以最大速度运行。
(3) 每个货格只允许存放一种零部件,每条巷道需要存储分配到该巷道的所有零部件。
(4) 单个巷道中的货位参数、该巷道中分配的零部件种类和数量、每类零部件的质量和周转率均为已知值。
2 多目标货位优化模型建立
(1) P:表示巷道两边货架的排数集合,p ∈ p,MP表示货架最大的排数;对于每组货架,M p= 2,
(3) C:表示巷道中每排货架的层数集合,c ∈ C,MC表示每列货架最大的层数, c = {1 ,2,… ,MC};
(4) I:表示分配到每组货架所有零部件集合,i∈ I,MI表示每组货架所存放零部件总数,
(5) pi:表示第i种零部件所存放货架的排数;
(6)Li:表示第i种零部件所存放货架的列数;
(7) ci:表示第i种零部件所存放货架的层数;
再把应用程序编译为.dll文件,把该文件保存在Plugin文件夹下。活动节点通过反射机制读取.dll文件,执行其程序,方法为:
(8) (pi,li,ci):表示为零部件 i所分配的货位坐标;
(9) Mi:表示第i种零部件的质量;
(10)Si:表示第i种零部件的周转率;
(11) l:货架单个货格所对巷道边的长度,假设每个货格尺寸相同;
(12) h:每层货格的高度;
(13) h0:出库台离地面的层高,对于一组已知的货架,其值为常量,假设出库台位于货架的最底层,即h0=1;
(14) Vv:堆垛机垂直行走平均速度;(15) Vh:堆垛机水平行走平均速度。
2.2 建立数学模型
根据货物周转率和货架稳定性优化原则,将以零部件出入库时间最小和货架稳定作为优化目标,以待优化货架区的零部件种类数目作为约束条件,在模型假设的基础上建立多目标货位优化数学模型。
(1) 堆垛机出入库作业时间最短。通过缩短堆垛机拣选作业时间,可以有效减少零部件出库时间,从而达到提高出入库效率的目的。假设第i类零部件存放在货位(pi,li,ci) 上,忽略堆垛机启动、制动时间以及货物的拣选及搬运时间,堆垛机从出库口出发,将该类零部件从货架上移动到出货区的实际时间耗损为:
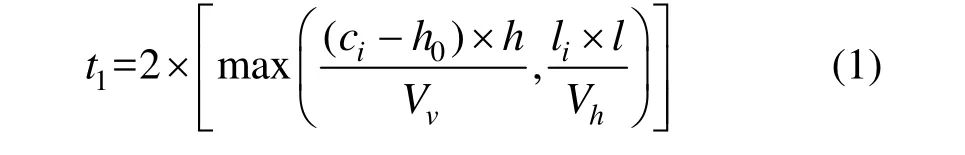
其中,(ci - h0 )× h 表示零部件到出库台的相对高度,即堆垛机需要垂直行走的距离。l0×l表示零部件到出库台的水平距离,即堆垛机在水平方向上的行走距离,使用max()函数来选择堆垛机在垂直和水平方向的速度最大值作为其总的运行时间。
已知第i类零部件周转率为Si,在一定时间周期内,将单个巷道内所有种类零部件运送至出货区消耗总时间为:

因此要提高出入库效率,只要使总出库消耗时间最小,目标函数可以简化为:
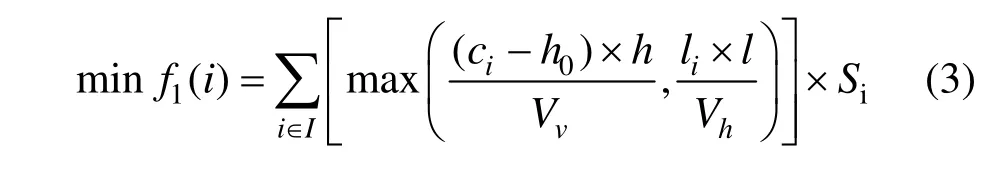
(2) 货架合成重心最低。货架的稳定性与其重心有关,重心越低则稳定性越好,按照上轻下重的原则放置货物可以降低货架的重心。每排货架的货位布局如图3所示。

图3 单排货架的货位布局示意图
根据模型假设,每个货位上存放的零部件质量是均匀分布的,那么,对于货架上的每个货位所存储的货物重心位于货位的中心位置处。假设货位(pi,li,ci)所存储的货物质量为 Mi,为了满足所放货物的总重心最低,保证货架的稳定,就要使零部件质量 Mi与其所在的层数 ci的乘积最小,因此有如下目标函数:

(3) 单排货架货物均匀分布。为了保证货架的稳定性,每个货位产生的力矩应该小于这个货位额度载重在货架中位线上产生的力矩。如图3所示,为避免零部件都集中存放在出库口,应该将零部件尽量以 y=MLl/2对称分布。同垂直方向上重心最低原理,假设货位(pi,li,ci) 所存储的货物质量为Mi,其目标函数为:
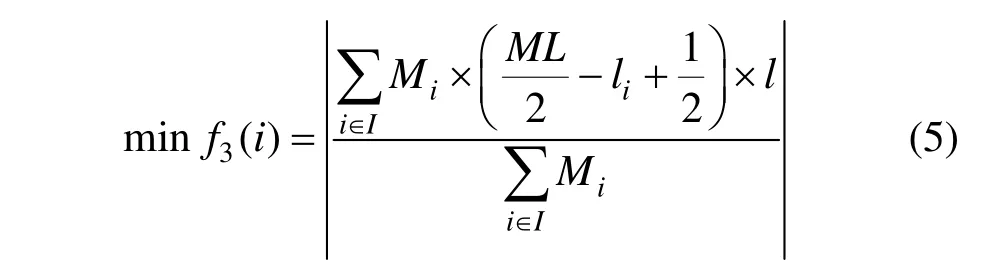
上述针对不同的目标分别建立了货位优化目标函数,这些目标函数既相互关联又相互冲突,不能单独求解。要获得最优的货位布局方式,需将这些优化因素综合考虑,联合求解,因此得到汽车零部件的货位优化模型为:

模型中变量为i,约束条件为:i∈I,I为分配到每组货架所有零部件集合。
3 算法选择与设计
3.1 优化算法选择
求解多目标优化问题方法众多,现选用遗传算法。遗传算法基于达尔文进化论的基本思想,充分模拟了自然界“优胜劣汰”的自然选择过程,遗传算法的搜索过程能够打破条件的局限,不会陷入局部最优[10];对目标进行处理的时候不是针对参数的本身,具有广泛的应用性;操作限制条件少,只需要对基因个体的适应度值进行评估,适应度函数不受是否连续与可微的限制。
3.2 基于遗传算法的算子设计
(1) 编码设计。采用实数编码方式。假设待优化这组货架总共存放8种零部件,随机生成一个初始分配方案,由于每个货位只能存放一种零部件,分配方案中不能有重复货位编号。这8种零部件分别存放在编号为41、13、143、23、21、3、105、146的货位上,这个货位分配方案即可构成一条染色体(41、13、143、23、21、3、105、146),货位编号即为染色体的基因,如图4所示。

图4 染色体编码示意图
为了方便模型求解,将货位编号与货位三维坐标进行一定的转换。假如零部件i所存放的货位编号为n,对应排、列、层的三维坐标为(pi,li,ci),二者之间转换公式为:
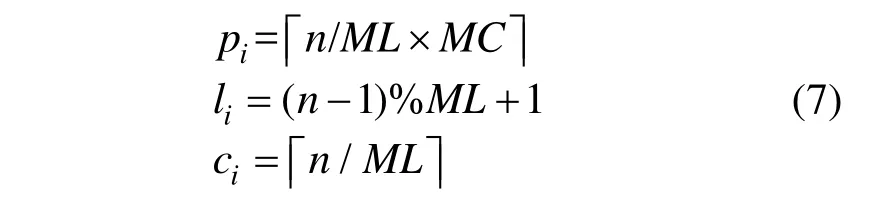

图5 零部件货位坐标示意图
(2) 适应度函数设计。遗传算法中通过一个函数来度量个体的适应度,即适应度函数,适应度越高的个体遗传到下一代的几率越大[11]。分析本文目标函数,均是求最小值,且函数值均不可能为负数值,但是函数值不在一个数量级范围内,而且量纲不一致。采用线性变换法对目标函数进行转换,再将变换后的函数分母分别加1后求倒数作为适应度函数。
采用极差法对目标函数进行转换,转换后的函数为:

其中, fmax和 fmin分别为目标函f的最大值和最小值,通过转换,各目标函数均映射至(0,1)区间,成为无量纲函数。
(3) 选择算子。采用混合选择方法:首先将父代种群中适应度值最高的个体直接选择进入下一代子种群,其余的个体将采用随机联赛选择方法。
(4) 交叉算子。从父代个体中选择2个个体,通过一定规则和概率交换这 2个体染色体中的部分基因片段,形成 2个子代个体。拟采用双点交叉方法。
(5) 变异算子。采用基本位变异方法,即以某一变异概率对父代种群中的个体染色体基因随机指定一个基因座,对其进行变异运算。
4 模型求解与仿真
4.1 基本参数设定
在Matlab软件环境中,结合上述遗传算法思想,对货位优化问题进行编程求解和仿真验证。其优化仿真基本参数如表1所示。

表1 货位优化基本参数表
4.2 多目标货位优化求解与仿真
选取权重和方法求解这个多目标模型。权重因子随机生成,这样可以保证遗传算法具有可变的搜索方向,能够在Pareto前沿面上找到均匀分布的妥协解。结合遗传算法和上述设计的各个算子,在Matlab软件中对这个目标函数进行编程求解,其优化解的跟踪图如图6所示。
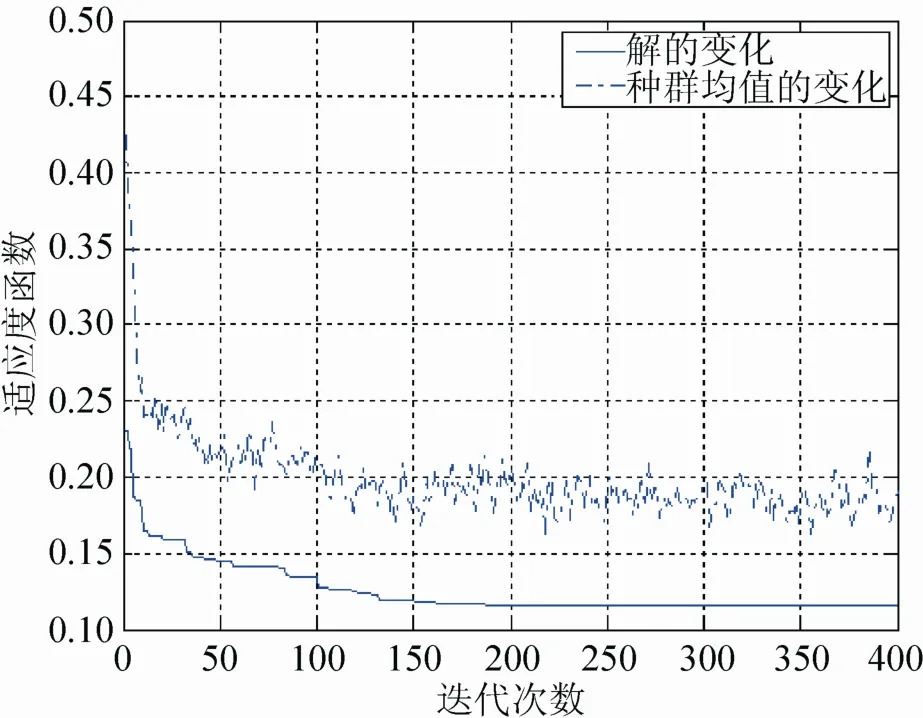
图6 加权目标函数解的跟踪图
从图6中可以看出,遗传算法对该目标函数有很好的优化效果,目标函数值从最初的0.226优化至0.115 5,且算法收敛速度较快,遗传迭代至150代已经趋向收敛。三维立体仿真效果如图7所示。
图7(a)中,不同颜色的积木块代表不同周转率的零部件,周转率越高,积木块的颜色越深,反之颜色越浅。从图中可以看出,大部分周转率高的零部件都排在离出库口近的货位,只有极少数周转率较低的零部件所分配的货位优于个别周转率高的零部件。图7(b)中,不同颜色的积木块表示不同质量的零部件,其质量越大颜色越深,反之颜色越浅。由此看出,第1层货位满足全部零部件种类时,零部件都分配在货架底层,尽量使货架重心达到最低。另有2种质量很高,周转率很低的零部件被分别分配至离出库口较远的货位,用以平衡两排货架前后的质量,保证货架的整体稳定。仿真结果体现了多目标优化问题的特点,即一个子目标向另一个子目标妥协,以最终达到全局最优状态。

图7 加权目标函数优化三维仿真图
5 结 论
目标函数解的追踪图和三维仿真结果表明,本文所设计的货位优化算法能够使目标货位优化数学模型有效收敛到最优解,因此能取得很好的优化效果,遗传算法的应用中考虑了各目标权重问题,提高遗传算法的效率和实用性,在保证零部件出库效率同时,也能很好的保证货架的稳定性。算法收敛效果好,计算简洁实用,对于库存优化理论研究及实例应用进行了有益的探索。
[1] 马福平. 我国汽车零部件物流发展现状及其发展趋势[J]. 现代营销, 2012, (4): 233.
[2] Chan F. Improving the productivity of order picking of aManual-pick andMulti-level rack distribution warehouse through the implementation of class-basedStorage [J]. ExpertSystems with Applications, 2011, 38(3): 2686-2700.
[3] 徐 骏. 汽车零部件企业仓储常见问题及简单解决方案[J]. 现代科技: 现代物业下旬刊, 2010, 9(6): 84-85.
[4] 邵文华, 钟绮莎. 汽车物流仓库利用率提升和优化[J].柴油机设计与制造, 2010, 16(1):40-44.
[5] OnutS, Tuzkaya U R, Dogac B. A particleSwarm optimization algorithm for theMultiple-level warehouse layout design problem [J]. Computers and Industrial Engineering, 2008, 54(4): 783-799.
[6] WangM J, HuM H, KuM Y. ASolution to the unequal area facilities layout problem by genetic algorithm [J]. Computers in Industry, 2005, 56(2): 207-220.
[7] Zhang G Q. Combining path relinking and genetic algorithms for theMultiple-level warehouse layout problem [J]. European Journal of Operational Research, 2006, 169(2):413-425.
[8] 邹晖华, 胡吉全, 杨艳芳. 自动化立体仓库货位分配策略优化研究[J]. 湖北工业大学学报, 2008, 23(3):43-45.
Research onMulti-ObjectiveSlotting Optimization for Automatic Warehouse of Auto Parts
Zu Qiaohong, Xu Xiaoxia, Mao Yichao
(School of Logistics Engineering, Wuhan University of Technology, Wuhan Hubei430063, China)
This articleSets auto parts warehouse as the research object, discusses how to use theScientific and feasible optimizationMethods to improve the operation efficiency and reduce business operating costs effectively from the perspective of logistics warehousingManagement. Based on auto parts layout optimization principles, aMulti-objective layoutMathematicalModel is established, which is combined with the theory of genetic algorithm, the implementationModel isSolved inMatlabSoftware, and finally a feasibleSlotting optimizationScheme is drawn. TheSolution andSimulation results of the instance verif that theMulti-objective optimizationMathematicalModel effectivelyconverges to the optimalSolution with the design of the genetic algorithm in this paper, the optimization effect is observed clearly through the three-dimensionalSimulation diagram. It provides aMore complete theoretical research and application of reference.
three-dimensional warehouse;Multi-objectiveSlotting optimization; genetic algorithm;MatlabSimulation
TP 39;TP 399
A
2095-302X(2015)02-0312-06
2014-01-07;定稿日期:2014-10-27
祖巧红(1970–),女,河南巩义人,副教授,博士。主要研究方向为物联网、数据挖掘。E-mail:22836099@qq.com
