基于寿命周期备件费用的系统可靠性优化设计

邵松世，李庆民，李　华

（1.海军工程大学科研部，武汉 430033；2.海军工程大学兵器工程系，武汉 430033）

基于寿命周期备件费用的系统可靠性优化设计

邵松世1，李庆民1，李华2

（1.海军工程大学科研部，武汉 430033；2.海军工程大学兵器工程系，武汉 430033）

针对以往系统可靠性优化研究中，系统费用仅包括研制成本，未考虑系统在列装期间运行费用的问题，应用一种基于寿命周期内备件需求估计的备件费用简易计算方法，对两种非线性可靠性-价格函数情况，以系统组成单元不可修、寿命分布服从指数规律为例，开展了以系统价格和备件费用之和最小为目标的可靠性分配优化研究。仿真试验结果表明：该方法简便易行，得到的优化方案更加合理，能避免单纯追求系统价格最低、却在装备使用阶段付出高昂费用的过度优化结果，能有效降低系统在全寿命期间的运行成本。

寿命周期；备件费用；可靠性优化；串并联系统；遗传算法

1　前言

在系统的可靠性设计工作中，要综合考虑系统各组成单元的重要度、复杂度、技术发展水平、工作时间和资源等因素，将系统的可靠性指标由上到下、由整体到局部，合理分配到该系统的分系统、设备及元件。

在可靠性优化的研究中，都会包括可靠度和费用这两个基本因素，其表现形式为：在费用额度约束下寻求可靠度最大或在满足可靠度要求下寻求费用最低。例如，文献应用遗传算法[1～4]、粒子群算法[5，6]、蚁群算法[7]等各种全局优化能力较强的算法研究解决复杂系统可靠性分配中的多目标优化、冗余优化等问题。文献[8～10]针对工程实践中系统费用随着可靠性指标提高出现的非线性增长现象，提出了多种形式的可靠性-费用非线性函数，以期能更准确地实现可靠性优化。在绝大多数的研究中，所谓费用在本质上都是指系统的研制成本（或者采购价格），鲜有将“费用”概念从价格延伸到系统在寿命期间的费用，例如使用阶段中产生的备件费用。文献[11]将武器装备可靠性费用定义为寿命周期内用于获取、提高装备可靠性而产生的费用，并将其进一步划分为可靠性工作费用和冗余费用两大部分，将装备使用、维修（维护）费用纳入可靠性费用范畴，开展了可靠性费用建模与优化研究工作。文献[12]提出了一种工程系统全局寿命可靠性优化模型，通过在总可靠度约束下追求当前造价和未来损失期望之和最小来寻求各子系统的最优可靠度分配。文献[13]具体讨论了由5个子系统、每个子系统由4种不同可靠度和寿命周期费用的部件组成的串-并联冗余结构的可靠性优化问题。但这些文献都没有涉及如何定量计算未来损失费用或寿命周期费用的方法，只是在假定已知未来损失费用或寿命周期费用的条件下开展优化研究。

系统备件是综合保障工作的重要内容。大量的实践经验表明：在使用阶段围绕系统开展的综合保障工作产生的维修费，备件的采购、存储、运输等费用往往大于系统价格。在20世纪60年代，美军国防预算的三分之一被消耗在装备的使用和维修方面，装备的保障费用在寿命周期费用中所占的比例高达60%，有的甚至达到70%～80%[14]，而这些费用其实与系统的可靠性是息息相关的，可以说是“设计”出来的。作为系统全寿命周期费用的一个重要组成部分，如何量化计算备件费用并用于系统可靠性优化是一个极具价值的问题。

本文应用一种基于寿命期间备件需求的备件费用简化计算方法，针对两种类型的可靠性-价格非线性函数，使用遗传算法进行优化计算，对比研究了仅考虑系统价格最少、同时考虑系统价格和寿命备件费用之和最少两种优化目标下，在系统可靠性优化结果方面的异同。

2　可靠性分配模型

为便于论述，本文统一使用单元、组件和系统来描述装备的层次结构。系统由组件构成，组件由单元构成。对于多组件串联系统，其可靠性可以通过两个途径进行提高[15～17]，即：a.使用更加可靠的单元；b.使用冗余技术，增加单元的冗余备份。

本文使用常用的串并联结构冗余技术[18]，讨论使用这两种途径用于改善系统可靠性的情况。

2.1备件费用估计

在系统设计之初，想准确预测其寿命备件数量是极其困难的。但是，如果知道组成系统所有单元的寿命分布规律及其参数、系统年平均工作时间、系统列装年限，那么就可以根据Cox D.R.提出的更新过程理论[19]，预测各个单元在寿命期间产生的故障次数。如果不采取修理措施的话，故障次数乘以价格即可认为是未来损失费用。

单元故障产生备件需求。当单元是不可修件时，则可认为备件数量应等于故障次数，此时乘以各单元的价格就可以估算出系统寿命期间的备件费用。对于可修单元而言，备件数量是故障次数的某种函数。对于寿命周期这种长时间预测而言，可以通过引入类似“平均可修理次数”这种经验型的统计概念来概略估计备件数量。总之，通过预测基于寿命故障次数的备件需求，可以在一定程度上定量估计寿命期间的备件费用。为便于论述，以下研究中假定系统的所有单元都不可修。此外，工程中常见的寿命分布类型主要有指数分布、威布尔分布、正态分布、伽马分布以及对数正态分布等。在以下研究中以指数分布为例进行论述。

假定某组件由n个相同的单元并联组成，其年平均工作时间为T1小时，列装年限为Y1年。单元的价格为c0，单元的寿命服从指数分布，其平均无故障间隔时间MTBF为t0。单元在时间t内的可靠度r计算方法见式（1）：

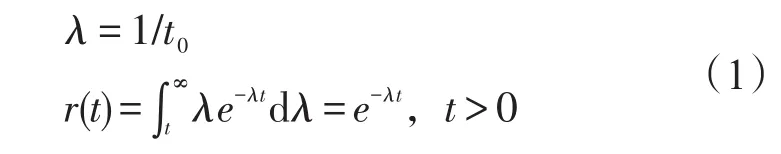
在寿命期间（装备列装期间）内该组件出现不大于k次故障的概率α计算方法见式（2）。概率α同时也是保障工作中所指的备件满足率。

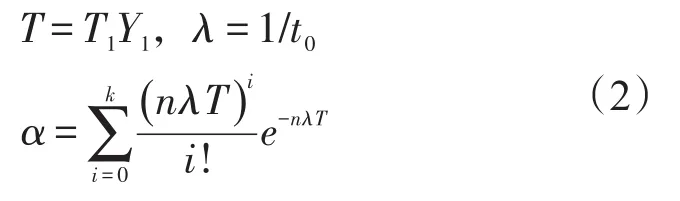
当备件满足率已知时，可根据式（2）计算故障次数k，则寿命期间的备件费用cb计算见式（3）：

本文参照中国人民解放军军用标准GJB 4355―2002《备件供应规划要求》，以单项法来计算系统的备件数量，即：平等看待所有单元、以同一个备件满足率标准逐一计算所有单元的备件数量。

2.2可靠性-价格函数

在文献[8～10]中，分别介绍了多种可靠性-费用函数。这些函数描述了可靠性与费用之间的关系，它包含了提高单元可靠性所花费的各种人力、物力和财力的总和。文献[8～10]中的费用在本质上是指系统的研制成本，或者说是系统的采购价格。为避免与本文中有关概念相混淆，在本文中称之为可靠性-价格函数。这些价格函数虽然形式不同，但具有一些相同的特点[10]：a.成本是关于可靠度的非线性增长函数；b.函数中都考虑到了单元i的可行度fi、最大可达可靠度ri,max、原有可靠度ri,min对单元i成本的影响。 fi是提高单元可靠性的可行度，取值范围在0到1之间，取值越大，说明提高该单元的可行性越大；c.要求的可靠度越高，成本增长越大。文献[9]中的价格函数形式见式（4）：

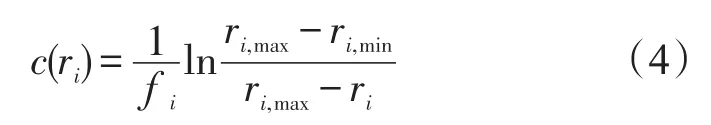
2.3串并联系统

本文研究的系统采用并联冗余技术中的串并联结构。设系统由m个独立组件串联而成，组件由若干数量的单元并联组成，系统组成见图1。

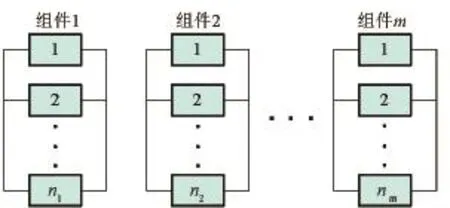
图1　串并联冗余系统框图Fig.1　Series-parallel system framework

通过可靠性优化，选择合适的单元可靠度ri和并联单元数目ni，在达到系统可靠度Rs满足设计指标R0要求：Rs≥R0的约束下，使系统的费用Cs最小。系统的可靠度Rs和组件的可靠度Ri计算方法见式（5）。

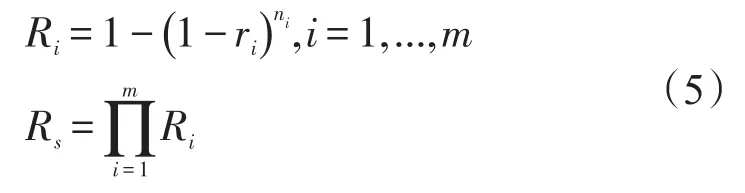
系统的价格Cp、备件费用Cb和总费用Cs计算方法见式（6）。

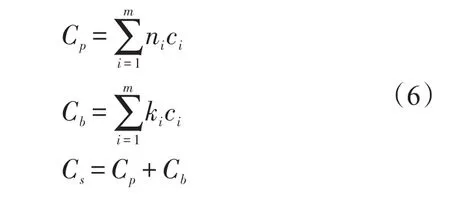
系统中第i个组件由ni个相同的单元并联而成，单元的可靠度、价格、备件数量为ri、ci、ki。

3　计算结果及分析

假定单元之间、组件之间相互独立。单元、组件和系统仅有两种状态——失效和正常工作。系统的价格是所有单元的价格之和。系统的总费用是系统价格与备件费用之和。

笔者针对文献[9，10]提出的两种不同类型的可靠度-价格函数，采用文献中提供的算例进行对比研究。文献[9，10]都只给出了不使用并联冗余技术（每个组件仅包含1个单元）、以系统可靠度满足要求为约束条件、以系统价格最低为目标的优化结果，该结果列在表1～表6的方案1列中。

表1　情形1的结果（算例一）Table 1　Result of case No.1（example 1）

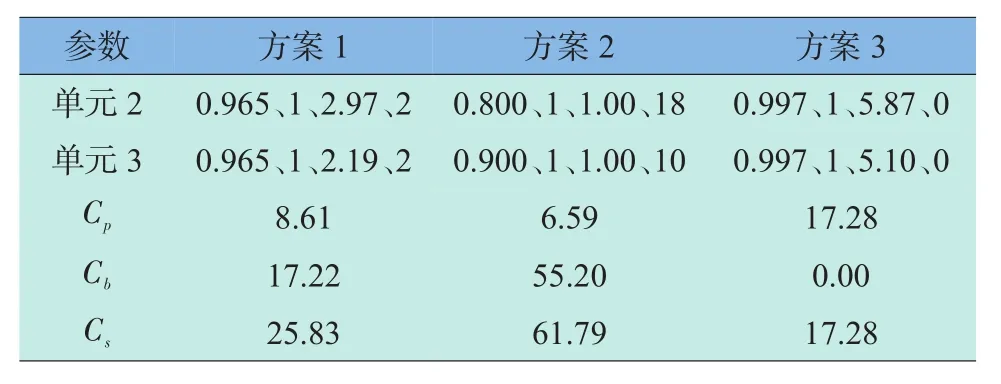
参数单元2单元3 Cp Cb Cs方案1 0.965、1、2.97、2 0.965、1、2.19、2 8.61 17.22 25.83方案2 0.800、1、1.00、18 0.900、1、1.00、10 6.59 55.20 61.79方案3 0.997、1、5.87、0 0.997、1、5.10、0 17.28 0.00 17.28

为便于对比分析，分别进行了下面两种类型的可靠性优化计算。

1）允许使用并联冗余技术（每个组件可并联使用多个同一类型的单元）、以系统可靠度满足要求为约束条件、以系统价格最低为目标的优化计算，该结果列于表1～表6的方案2列中。

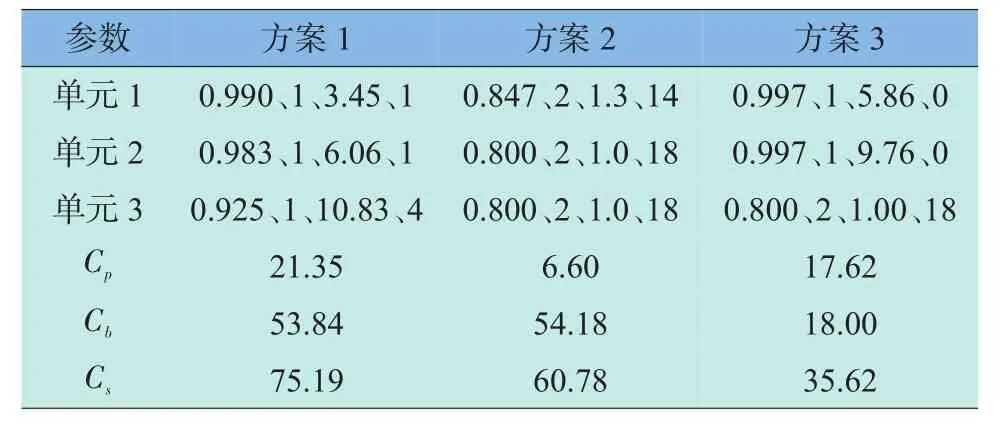
表2　情形2的结果（算例一）Table 2　Result of case No.2（example 1）

2）允许使用并联冗余技术、以系统可靠度满足要求为约束条件、以系统总费用最低为目标的优化计算，该结果列于表1～表6的方案3列中。

表3　情形3的结果（算例一）Table 3　Result of case No.3（example 1）

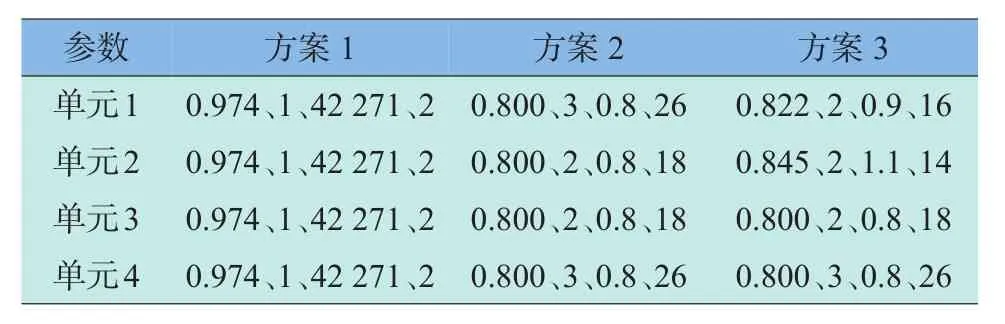
表4　情形1的结果（算例二）Table 4　Result of case No.1（example 2）

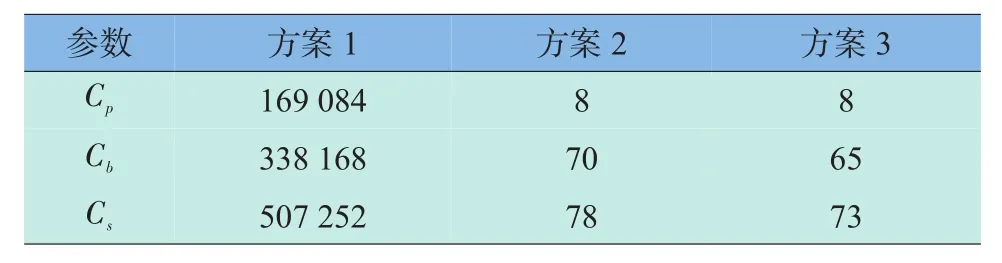
参数Cp Cb Cs方案1 169 084 338 168 507 252方案2 8 70 78方案3 8 65 73

表5　情形2的结果（算例二）Table 5　Result of case No.2（example 2）

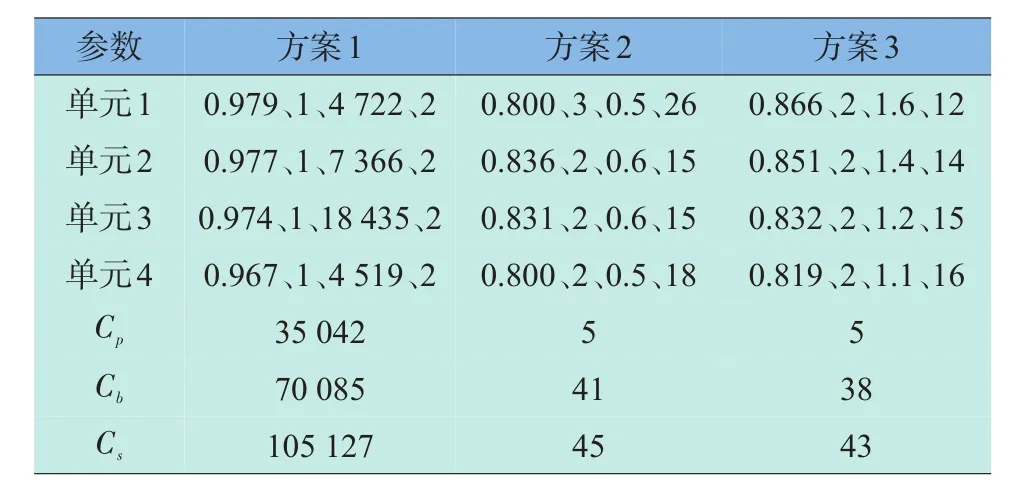
表6　情形3的结果（算例二）Table 6　Result of case No.3（example 2）

本文使用MATLAB 7.1 SP3版提供的遗传算法工具箱进行可靠性优化计算，遗传个体由各组件中的单元可靠度ri和单元数量ni组成，采用实数编码，每代个体数量为5 000，遗传进化10 000代，其他参数采用缺省设置。

4　算例一及分析

本算例采用文献[9]中的算例，其装备价格与可靠性的函数关系为对数关系。由于当单元i的可靠度ri分配为ri,min时，单元价格ci如由式（4）计算则等于0，这是不合理的。为此，每个单元增加一个基准价格将式（4）修正为式（7）。在后面的计算中，取

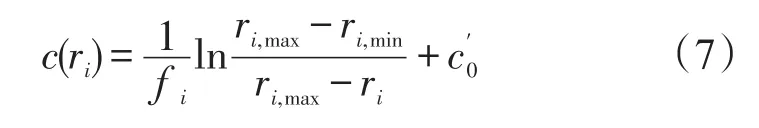
文献[9]的计算参数如下。

某系统由三个单元串联组成，可靠性指标为0.90，试将该指标分配给各单元。

情形1：单元1的原有可靠度r1,min为0.7；单元2的原有可靠度r2,min为0.87；单元3的原有可靠度r3,min为0.9。三个单元的可行度均为0.9，最大可达可靠度均为0.999。

情形2：单元1的可行度 f1为0.9；单元2的可行度 f2为0.5；单元3的可行度 f3为0.1。三个单元的原有可靠度均为0.8，最大可达可靠度均为0.999。

情形3：单元1的最大可达可靠度r1,max为0.999；单元2的最大可达可靠度r2,max为0.98；单元3的最大可达可靠度r3,max为0.95。三个单元的可行度均为0.9，原有可靠度均为0.8。

当笔者提到系统的可靠度指标时，一般都有一个与之相对应的时间值。由于文献[9，10]都没有提及该值，因此在本文中笔者假定该时间值为500 h，系统的年平均工作时间为1 500 h，系统的列装时间为10 a。

对上述3种情形的优化方案，计算其系统价格、备件费用和总费用，结果见表1～表3。表中第2行～第4行中以数组形式列出了分配给该单元的可靠度ri，构成该组件的单元数量ni，单元的价格ci和寿命期间该单元的备件数量ki。

表1表明：如果优化计算时仅仅考虑系统的价格，方案2由于采用并联冗余技术，能显著降低单元的可靠度要求，从而明显减少单元和系统的价格，方案2“优于”方案1。但在系统使用期间，单元的可靠度过低会导致其故障次数显著增大，进而带来较高的备件费用，出现常见的“便宜无好货”的现象。方案3的结果表明：尽量提高单元的可靠度是情形1实现总费用最低的系统研制技术途径。

表2表明：情形2时方案2表明采用并联冗余技术后，不但系统的价格明显下降，总费用也略少于方案1。而方案3则“融合”了方案1和方案2的“优点”，通过有选择性地提高单元1和单元2的可靠度、单元3采用并联冗余技术，进一步对方案2实现了优化，显著降低了总费用。

表3表明：考虑到寿命期间备件需求估计结果必然存在误差，对于情形3，方案1和方案3在总费用上并无显著的区别。方案3实际上给出了一种混合并联冗余技术和提高单元可靠度的技术方案。方案2与方案1相比则是价格优势明显、长期费用高昂的方案，它很好地说明了在可靠性优化中仅考虑系统价格时存在“越优化、越倒霉”的风险。

5　算例二及分析

算例二采用文献[10]中的算例。文献[10]中的可靠度-成本函数为指数函数，见式（8）：

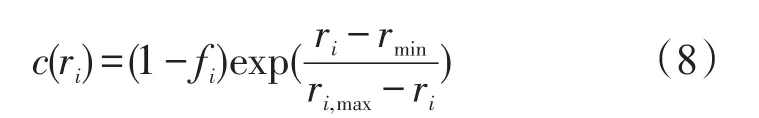
文献[10]的计算参数如下：

系统由4个单元串联而成，所有单元最初可靠度均为0.8，要求系统可靠度达到0.90。

情形1：所有单元的最大可靠度均为0.99、可行度均为0.2时的分配值。

情形2：所有单元的最大可靠度均为0.99，单元1的可行度 f1取0.1，单元2的可行度 f2取0.4，单元3的可行度 f3取0.6，单元4的可行度 f4取0.9时的分配值。

情形3：所有单元的可行度均取0.5，单元1的最大可靠度r1,max取0.999，单元2的最大可靠度r2,max取0.995，单元3的最大可靠度r3,max取0.99，单元4的最大可靠度r4,max取0.985时的分配值。

对上述3种情形的优化方案，计算其系统价格、寿命期间的备件数量和备件费用，结果见表4～表6。

与算例一不同，在算例二中：与方案1相比，表4～表6中方案2和方案3呈现一边倒的绝对性优势。如果暂不质疑式（7）可能存在合理性问题的话，造成上述结果的根本原因在于其非线性费用函数是指数增长速度，单元最大可靠度与最小可靠度之间的价格比例高达104以上，足以抵消较低可靠度带来的负面效果——其备件数量是单元取最大可靠度时的10倍左右。该结果表明：在可靠性-价格函数中，常见的对数、线性、指数函数形式下，其最重要的含义是随着可靠度提高价格的增长速度。对于类似算例二（随着可靠度的提高而价格急速增长的情况），在进行可靠度分配优化时，可以不考虑寿命费用的影响，“给各单元分配较低的可靠度+并联冗余技术”是一个绝对不能忽视的系统研制方向。

在大量计算和分析比较研究后，笔者等认为：至少在系统的设计初期，由于在费用方面存在较多的不确定情况，在可靠性优化中不必过于纠结是否得到最优解，工程上更应该关注优化方法是否简便易行、影响因素是否考虑齐全、优化方案对应的技术实现方向等方面。这是因为一方面，对于像遗传算法、粒子群算法、蚁群算法等启发式搜索算法而言，其本质上都是随机搜索，只不过能以更大的概率找到最优解的邻域解而已。另一方面，优化中使用的无论是可靠性-价格函数还是备件费用估计，都是一种对现实或未来情况的拟合与预期，与实际情况必然存在差距。在工程研制中可靠度和成本费用绝不可能如上述函数表达的那样“连续”——各个单元不可能出现价格始终“跟随”可靠度连续变化、精确对应的情况，研究人员更应该关注这些函数所表达的成本增长速度。对寿命期间备件需求估计而言，这种长期的估计结果只能是粗略的、不精确的，误差即便高达20%～50%都是可能的。因此，工程研制人员更应该关注其优化方案后面代表的系统技术实现方向。

6　结语

研究结果表明：该方法简便易行，从全寿命周期经济效益的角度，根据不同可靠性-价格函数所代表的价格随可靠性提高而提高的增长速度，得到更为经济合理的优化方案，能在系统设计初期阶段辅助确定系统实现技术方向：

1）对可靠性-价格函数类似对数形式的、具有价格随可靠性增长速度较低的系统，能更合理地使用提高单元可靠性和并联冗余技术两种方法，避免单纯追求系统价格最低而带来的系统后期使用费用高昂的过度优化问题；

2）对可靠性-价格函数类似指数形式的、具有价格随可靠性快速增长的系统，可优先考虑以并联冗余技术进行系统可靠性分配和系统实现方向。

[1]陈雅菊.基于多目标遗传算法的复杂系统可靠性冗余优化[J].舰船科学技术，2010，32（9）：101-103.

[2]马成业，黎锁平，杨胜良.模糊多目标可靠性优化设计的遗传算法[J].兰州理工大学学报，2009，35（1）：156-158.

[3]姜封国，安伟光.基于混合遗传算法的随机结构可靠性优化设计[J].华南理工大学学报（自然科学），2008，36（1）：152-156.

[4]张铁柱，滕春贤，韩志刚.遗传算法在系统可靠性优化中的应用[J].控制与决策，2002，17（3）：378-381.

[5]阮旻智，李庆民，王红军，等.人工免疫粒子群算法在系统可靠性优化中的应用[J].控制理论与应用，2010，27（9）：1253-1255.

[6]于繁华，杨威，张利彪.基于模糊的多目标粒子群优化算法及应用[J].计算机仿真，2007，24（2）：153-156.

[7]程世娟，卢伟，何平.复杂系统可靠性冗余的蚁群优化算法[J].机械强度，2010，32（1）：64-67.

[8]和麟，黄潇瑶，马存宝.基于费用函数的航电系统可靠性优化分配方法[J].计算机与现代化，2012（10）：1-4.

[9]刘飞，张为华.基于费用函数的系统可靠性优化分配方法[J].机械设计与制造，2005（11）：11-12.

[10]鹿祥宾，李晓钢，林峰.复杂系统的可靠性分配和优化[J].北京航空航天大学学报，2004，30（6）：565-568.

[11]黎放，费奇，王威.武器装备可靠性费用研究[J].系统工程与电子技术，2005，27（7）：1253-1255.

[12]杜凤娥，刘立伟.关于工程系统全局全寿命优化模型的讨论[J].系统工程与电子技术，2005，27（2）：267-269.

[13]王建成.基于遗传算法的系统可靠性优化[J].装备指挥技术学院学报，2005，16（4）：112-115.

[14]Authur J Alexandar.The cost and benefits of reliability in military equipment[R].AD-A207344，1989.

[15]段平，胡捷.基于MATLAB的串联系统可靠性整数优化[J].信息与电子工程，2009，7（5）：476-478.

[16]赵剡，白雪峰.惯性导航系统冗余设计与可靠性分析[J].航空兵器，2006（1）：15-17.

[17]张家海，孙枫，徐耀群，等.系统可靠性最优化部件的可靠度和冗余数确定[J].哈尔滨理工大学学报，2001，6（1）：69-72.

[18]张志华.可靠性理论及工程应用[M].北京：科学出版社，2012.

[19]Cox D R．Renewal Theory[M].New York：Methuen&Co Ltd/John Wiley&Sons Inc，1962．

Design on system reliability optimization based on the spare parts’cost of life cycle

Shao Songshi1，Li Qingmin1，Li Hua2
（1.Department of Researching，Naval University of Engineering，Wuhan 430033，China；2.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

There are problems in the previous system reliability optimization study because of system cost only including system price and without considering the system operation cost during the life cycles.We employ a simple calculation method of the spare parts’cost based on the estimation for spare parts demand during the whole life cycle，in the condition of two kinds of nonlinear reliability-price function，system composition units being not repaired and units’life time obeying exponential distribution，research system reliability allocation optimization as the goal of minimizing the sum of system price and spare parts cost.The simulation results show that the method is simple，convenient and feasible，and can effectively avoid over optimization when only pursuing the lowest system price at the expense of the whole life cycle cost. The system reliability optimization scheme，which based on the spare parts’cost of life cycle，can efficaciously reduce system operation cost during the life cycles.

life cycle；the cost of spare parts；reliability optimization；series-parallel system；genetic algorithm

V215.7

A

1009-1742（2015）05-0025-06

2015-03-09

邵松世，1979年出生，男，山东青岛市人，工程师，主要研究方向为装备维修保障资源规划；E-mail：369698199@qq.com