基于单轴气浮台的载荷运动特性测试的设计实现与分析

2015-12-01彭瑞谢任远

中国科技纵横 2015年9期

关键词：转动惯量傅里叶单轴

彭瑞谢任远

(上海航天控制技术研究所,上海 201109)

基于单轴气浮台的载荷运动特性测试的设计实现与分析

彭瑞谢任远

(上海航天控制技术研究所,上海 201109)

为验证某卫星转动载荷的大角动量补偿功能是否满足实际使用需求,设计出基于单轴气浮转台,利用单轴气浮台测角装置和陀螺组合,对转动载荷在不同质量(转动惯量相同)、不同转动角速度的情况下的运动特性进行测量的地面试验系统,并以某一工况为例,得出载荷转动的时域与频域特性。试验结果为大角动量补偿功能的设计完善提供了依据,对卫星后续研制意义重大。

单轴气浮台频谱分析运动特性地面试验系统

1　引言

随着卫星载荷的不断发展和卫星平台技术的日渐成熟，载荷对卫星平台的要求越来越高，两者的关系逐渐从载荷适用平台发展为载荷决定平台，由此给卫星平台的研制工作提出了更高的要求。为了降低研制风险，需要通过各种类型的大量地面仿真试验对系统方案进行验证[1]。

某卫星载荷在卫星入轨后一直处于匀速转动状态，其转动产生的角动量由卫星姿轨控分系统进行长期补偿，因此探测头部旋转角速度的特性，直接影响卫星姿态稳定度指标。

本文根据某卫星载荷的运动特性，构建了一个基于单轴气浮台的对载荷在不同质量(转动惯量相同)、不同转动角速度的情况下的运动特性进行测量的地面试验系统，同时对测试出的转速进行频谱分析，得到载荷转动的时域与频域特性，为优化角动量补偿控制设计提供了依据。

2　频谱分析理论及在Matlab中的应用

控制系统的设计应该从分析性能要求开始，而频谱分析是性能分析的基础。另外，频谱分析也是设计和分析中常用到的一种数据处理手段。因此，设计者不仅应该知道频谱的概念，还应该掌握频谱的分析方法[2]。

2.1傅里叶级数

对于周期为T的周期函数f(t):

如果f(t)满足狄里赫利条件:在区间T上有界，且仅有有限个极大值和极小值，则f(t)可用收敛的傅立叶级数来表示。

三角函数形式的傅里叶级数为

上式的系数为

控制系统中使用复数形式的傅里叶级数

其中的系数kc为

c为复数，一般可表示为如下形式

从(5)式可知kc和-kc为共轭复数，对于其中的每一组可以写成

式(7)表明，当用复数形式表示是，复系数kc的幅值ka表示了第k次谐波的幅值(幅值为2ka)，而kc的相角kβ则为该次谐波的相移。这种用复数形式来表示的谐波常称为复数正弦。

用傅里叶级数来表示函数f(t)，无论是实数形式还是复数形式，都是将f(t)看成是由各次谐波所组成。傅里叶级数的系数表示了各次谐波的幅值和相位，这些系数的集合称为频谱。

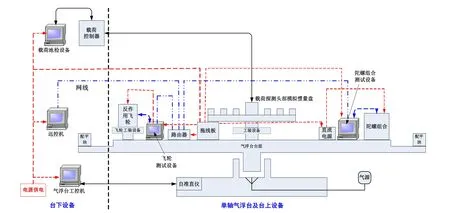
图1　试验系统组成

2.2傅里叶积分和傅里叶变换

控制系统分析中，经常遇到非周期函数，这时傅里叶级数就不能应用了，但可以用傅里叶积分来处理[2]。

式(8)称为傅里叶积分，式(9)中的F(j)ω称为函数f(t)的傅里叶变换。

设将f/2ωπ=作为频率的横坐标，这时式(8)改写为:

对于(8)式，按照积分的概念可得:

或者可以写为:

图2　转速波动量测试结果对比图

图3　转速频域分析结果对比

傅里叶积分将一个非周期函数f(t)分解为各次谐波，每一个谐波的幅值由(8)式可知为:

这幅值为无穷小，所以一般用相对幅值F(j)ω来表示其频谱。这就是说，傅立叶变换F(j)ω表示的是该非周期信号谐波的分布特性，故F(j)ω称为信号的频谱特性，简称为频谱。

傅里叶变换使得我们可以从频谱的角度来分析信号。

2.3频谱分析在MATLAB中的应用

离散傅里叶变换是进行频谱分析的基本工具，在实际中得到广泛应用的是快速傅里叶变换(F F T算法)。现在F F T已可以用MATLAB软件中的fft函数来进行计算，这个函数做的是下面的变换

式(14)中W=e-j2π/N，N是x的点数(即数据长度)。

实际使用中需要注意FFT算法与其它函数一起运用。本文中频谱分析的函数算法如下:

3　试验系统设计

气浮台依靠气源提供的压缩空气在气浮轴承与轴承座之间形成气膜，从而使气浮台的转台浮起，实现近似无摩擦的相对运动条件，以模拟卫星载荷在外层空间所受干扰力矩很小的力学环境[2]。某卫星载荷在卫星入轨后一直处于匀速转动状态，为测试其运动特性，设计的试验系统组成如图1所示。本试验中气浮台为单轴精密气浮台;反作用飞轮用于标定图1所示的气浮台总的转动惯量;陀螺组合用于测量载荷转动时气浮台的相对转动角速度;载荷探测头部模拟惯量盘用于模拟载荷探测头部的转动(质量可调、转动惯量相同)，由载荷伺服控制器控制其转动角速度。

图1中，载荷探测头部模拟惯量盘、动量轮通过工装设备固连于单轴气浮台上，陀螺组合、反作用飞轮地面试验设备、陀螺组合地面试验设备直接放置在气浮台上;载荷伺服控制器、载荷地检设备放置于台下。载荷伺服控制器通过载荷地检设备进行供电、控制与相关通讯;反作用飞轮、陀螺组合分别通过专用测试设备进行供电、控制与相关通讯;单轴气浮台通过配平块进行配平，通过自准直仪进行测角与测角速度;远控机通过网络控制飞轮和陀螺的地面软件，用以发送指令和存储数据。载荷的台上台下连接电缆加工材料采用柔性较好软线或散线，通过吊装设备从气浮台中心上方垂下，以减小电缆产生的扭矩对试验的影响。

4　试验数据分析和处理方法

4.1气浮台整体转动惯量JO的计算

已知反作用飞轮的转动惯量是J1=0.0465kgm2，转速为ω1为飞轮转速;台体转动惯量设为J0，转速ω0为气浮台自准仪的测量值;根据动量守恒公式J0*ω0=J1*ω1，可计算出气浮台体的转动惯量J0= (J1*ω1)/ω0。

试验中共进行了4组测试，分别根据反作用飞轮0rpm-＞1000rpm、1000rpm-＞0rpm、0rpm-＞-1000rpm和-1000rpm-＞0rpm四种工况下的气浮台转速数据(△ω01、△ω02，△ω03，△ω 04)，算出台体的转动惯量(J01、J02，J03，J04)，取平均值作为气浮台体的转动惯量。

4.2载荷转速波动量的计算

载荷探测头部转动惯量J2取理论值19 kgm2，转速设为ω2;台体转动惯量为J0(4.1中计算值)，转速ω0为气浮台自准仪测量值;根据动量守恒公式J0*ω0=J2*ω2，可计算出ω2=(J0*ω0)/J2。

试验中分别在模拟惯量盘质量60kg和90kg条件下，进行了转动角速度108°/s、120°/s、150°/s共六种工况的测试;根据气浮台转速数据(陀螺数据和自准仪数据)，计算并画出每一种工况下三个转动角速度波动量(载荷自身采集，陀螺数据换算和自准仪数据换算)的数值对比曲线，得出每种工况下的载荷探测头部转动角速度波动量范围。

为更好的反映运动特性，分别对不同工况下的陀螺转速、载荷转速、气浮台转速利用FFT进行频谱分析，从频率角度进一步分析其运动特性。