船舶搁浅模糊故障树的灰色模糊关联分析

陈婷婷， 施朝健， 雷 琴(上海海事大学 商船学院，上海 201306)

船舶搁浅模糊故障树的灰色模糊关联分析

陈婷婷， 施朝健， 雷 琴
(上海海事大学 商船学院，上海 201306)

为解决应用传统故障树方法分析船舶搁浅事故时带有不可避免的灰色性和模糊性的问题，在分析船舶操纵性搁浅故障树的基础上，对底事件发生概率进行模糊化，建立船舶搁浅模糊故障树。引入灰色模糊关联分析方法，对模糊故障树进行定性和定量分析，根据故障树的最小割集、底事件的结构概率重要度和模糊重要度，计算各故障模式与顶事件的关联度，关联度越大，说明其对顶事件发生的影响越大。最后，综合考虑各底事件在关联度较大的最小割集中的分布情况及其模糊重要度情况，找出对顶事件发生的影响较大的底事件和故障模式，为降低顶事件发生概率制定相关风险控制措施提供参考依据。

水路运输；灰色模糊关联；模糊故障树；正态模糊数；模糊重要度；结构概率重要度；船舶搁浅

船舶搁浅事故一旦发生，造成的危害通常较为严重，导致船舶沉没全损的可能性非常大。据统计，2012年我国发生的水上交通事故中，涉及搁浅触礁事故的船舶达到46艘，占事故涉及船舶总数的7.87%(见表1)。[1]因此，需要对船舶搁浅事故进行分析，研究船舶搁浅的故障模式，找出最容易导致船舶搁浅事故发生的原因和故障发生模式，为制定船舶搁浅风险预控措施提供参考，进而降低船舶搁浅事故发生的概率。

目前，故障树分析(Fault Tree Analysis，FTA)和事件树分析(Event Tree Analysis，ETA)已被应用到船舶搁浅事故的分析中，并取得了一定的研究成果[2-3]，但在应用FTA和ETA进行分析时，因缺乏相关数据库和精确的数据描述，涉及的各个底事件的发生概率难以通过确定的值表示，而主要采用相关领域的统计数据和近似数据或借助专家的判断，从而导致这些概率值带有一定的不确定性，包括模糊性和灰色性。因此，简单基于这种概率得到的顶事件发生概率不具有实际利用价值，应充分考虑系统的模糊性和灰色性。

表1 2012年我国水上交通事故涉及船舶艘数统计表

对此，在建立船舶操纵性搁浅故障树的基础上，对故障树进行正态模糊化定性和定量分析，以底事件的模糊重要度为参考序列，以最小割集组成的特征矩阵为比较序列，以底事件的结构概率重要度为权重序列，根据灰色模糊关联模型计算出各个最小割集所代表的故障模式与顶事件发生的关联度；同时，综合分析出模糊重要度较大且在与顶事件关联度较大的最小割集中出现的频率也较大的底事件，从而为制定船舶操纵性搁浅事故预防措施提供更为全面、直观的参考。

1 基于灰色模糊关联的模糊故障树分析方法

基于灰色模糊关联的模糊故障树分析方法流程见图1：首先确定顶事件(T)；然后逐层分析，直至找出事故的基本原因，即故障树的底事件(X)；最后确定底事件的模糊概率，并对故障树进行定性和定量分析。

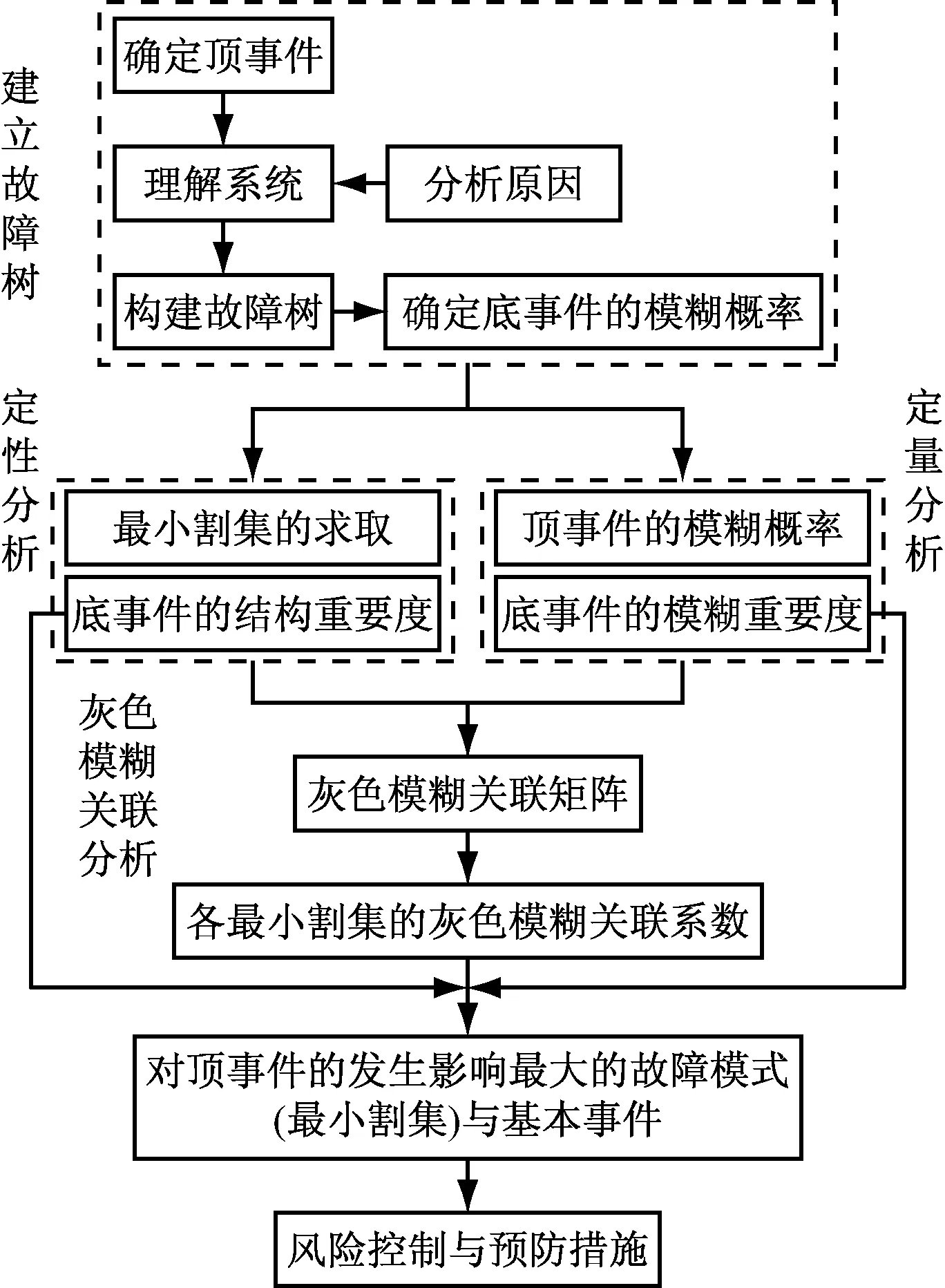
图1 模糊故障树分析方法流程

1.1底事件模糊概率的确定

由于确定底事件概率的过程中带有一定的不确定性，因此采用定义在概率空间中的模糊数来表示底事件的发生概率。[4]这里采用正态模糊数是因为正态分布是一种较为常见、应用较广的隶属度函数形式，且正态隶属度函数曲线是连续、非线性的，曲线两端延伸至无穷远，更有利于处理模糊性问题。由正态模糊隶属度函数的曲线可知：与其他隶属度函数相比，在确定某参量的模糊区间后，当取较高的隶属度时，采用正态分布能收集更多隶属度高的信息；而当取较低的隶属度时，采用正态分布能屏蔽更多隶属度低的信息。此外，其参数简单，仅由均值μ和方差δ来决定。设在论域R上的一个模糊数的隶属函数为

(1)

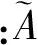
1.2模糊故障树的定性与定量分析

1.2.1求取故障树的最小割集

具有n个底事件的故障树的结构函数可表示为Φ(X1,X2,…,Xn)，为各底事件的逻辑运算形式。对结构函数进行简化运算，求出故障树的最小割集记为(T1,T2,…,Tm)。

1.2.2计算顶事件的模糊概率

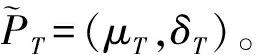
1.2.3计算底事件的结构概率重要度

底事件在最小割集中的贡献形式可分为2类。

(1) 虽然底事件构成的故障模式较少，但发生概率较高，属于主导型事件；

(2) 虽然底事件发生概率较小，但是很容易与其他事件结合起来诱发多种故障模式，属于触发型事件。

因此，以底事件的结构概率重要度系数ek(k=1,2,…,n)来阐述其在整个系统中的重要性；同时，考虑该事件对顶事件发生概率的影响及其在所有割集结构中的贡献。

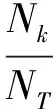
(2)

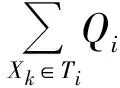
随后对ek序列进行归一化处理，作为各底事件在系统中的权重序列。

(3)

1.2.4计算底事件的模糊重要度

(4)

1.3灰色模糊关联模型与关联度计算

1.3.1确定比较序列和参考序列

用特征向量代表故障树中的m个最小割集，从而构建一个故障树的故障模式特征矩阵T，包含了m个比较序列。

(5)

式(5)中：当底事件Xk出现在最小割集Ti中时，xi(k)取值为1，否则为0。

参考序列的选取应与比较序列对应，应能体现底事件在系统中的重要度，因此用各底事件的模糊重要度代替。把式(4)计算出的各底事件的模糊重要度均值化处理后作为参考系列X0(k)。

(6)

(7)

1.3.2计算灰色关联系数

比较序列中的元素xi(k)与参考序列中的元素x0(k)之间的灰色关联系数为

式(8)中：ρ∈[0,1]为分辨系数，作为Δmax的系数或权重，其取值大小在主观上反映了研究者对Δmax的重视程度，在客观上体现了系统的各个因子对关联度的间接影响程度。因此，ρ的取值应充分体现关联度的整体性，且具有抗干扰作用。文献[7]提出了ρ的取值规则，记Δv为所有差值绝对值的均值。

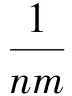
(11)

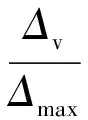
1.3.3计算灰色关联度

(1) 加权得到最小割集Ti(i=1,2,…,m)的灰色关联度为

(12)

灰色关联度越大的最小割集所代表的故障模式对顶事件发生的可能性影响越大；

(2) 观察灰色关联度较大的最小割集中所包含的底事件情况，结合各底事件的模糊重要度排序情况，综合得出模糊重要度较大且在灰色关联度较大的最小割集中出现频率也较高的底事件，该类底事件对顶事件的发生影响较大；

(3) 综合对顶事件影响较大的故障模式及底事件，制定相应的风险预防管控措施。

2 船舶操纵性搁浅模糊故障树的灰色模糊关联分析

挪威船级社(Det Norske Veritas, DNV)大致将船舶搁浅事故分为操纵性搁浅(Powered Grounding)和漂移式搁浅(Drift Grounding)两类[2,8-9]，其中操纵性搁浅占主导地位，且涉及诸多人为因素，可在一定程度上对其进行预控。因此，主要分析操纵性搁浅事故。

操纵性搁浅可描述为以下两种情况。

1) 理想的航道不安全造成的操纵性搁浅，主要由航道计划过程中的失误引起。

2) 船舶偏离理想的航道造成的操纵性搁浅，主要由航行过程中的失误引起。

结合事故统计资料[1]和船舶搁浅触礁事故原因的相关研究[10-13]得出：导致船舶搁浅事故的因素涉及自然条件、交通条件、航路条件、本船状况、航海图书资料条件、船员素质及人员管理情况等多个方面，主要的失误体现在航线、船位、资料信息、操作及管理等方面。对此，借鉴文献[8]和文献[9]中建立的船舶操纵性搁浅事故树进行相关分析，并对其进行扩展和完善。例如，对故障树中“船舶偏离了理想的航道”进行分析，造成该失误的原因包括没有检测到船位失误、检测到船位失误但没能及时修正过来。对于船位的检测与估计，主要依靠有效的信息、完善的设备手段和合理的操作管理。因此，对中间事件“错误没有测量出来”进行分析时，考虑的因素包括“没有合理有效的信息”和“设备故障或没有合理使用”。由于该层事件主要分析的是船位的检测与估计是否发生失误，因此所谓的设备指的是船舶位置方面的，设备的失误包括“船舶定位错误”“位置传感器错误”和“位置估计错误”。而“检测到船位失误但没能及时修正过来”的主要原因则在管理与操作方面。

综上分析，建立图2所示的船舶操纵性搁浅故障树。并利用前文研究的模型对其进行分析。

2.1建立船舶操纵性搁浅故障树

图2中，故障树的顶上事件T为船舶操纵性搁浅事故，经过逐层分析，得出故障树的18个底事件X1～X18。

图2 船舶操纵性搁浅故障树

2.2求故障树的最小割集

由图2得出该故障树的结构函数为

Φ(X1,…，X18)=(X1X2+X3+X4)X5+X6(X7+X8+X9+X10)+[X11(X12+X13+X14)+X15](X16+X17+X18)

求得其最小割集共19个，分别为：

T1={X1,X2,X5}，T2={X3,X5}，T3={X4,X5}，T4={X6,X7}，T5={X6,X8}，T6={X6,X9}，T7={X6,X10}，T8={X11,X12,X16}，T9={X11,X12,X17}，T10={X11,X12,X18}，T11={X11,X13,X16}，T12={X11,X13,X17}，T13={X11,X13,X18}，T14={X11,X14,X16}，T15={X11,X14,X17}，T16={X11,X14,X18}，T17={X15,X16}，T18={X15,X17}，T19={X15,X18}。

2.3确定底事件和顶上事件的模糊概率

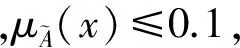
(13)

得出δ=0.329 5μ，则可计算出底事件的模糊概率(见表2)。

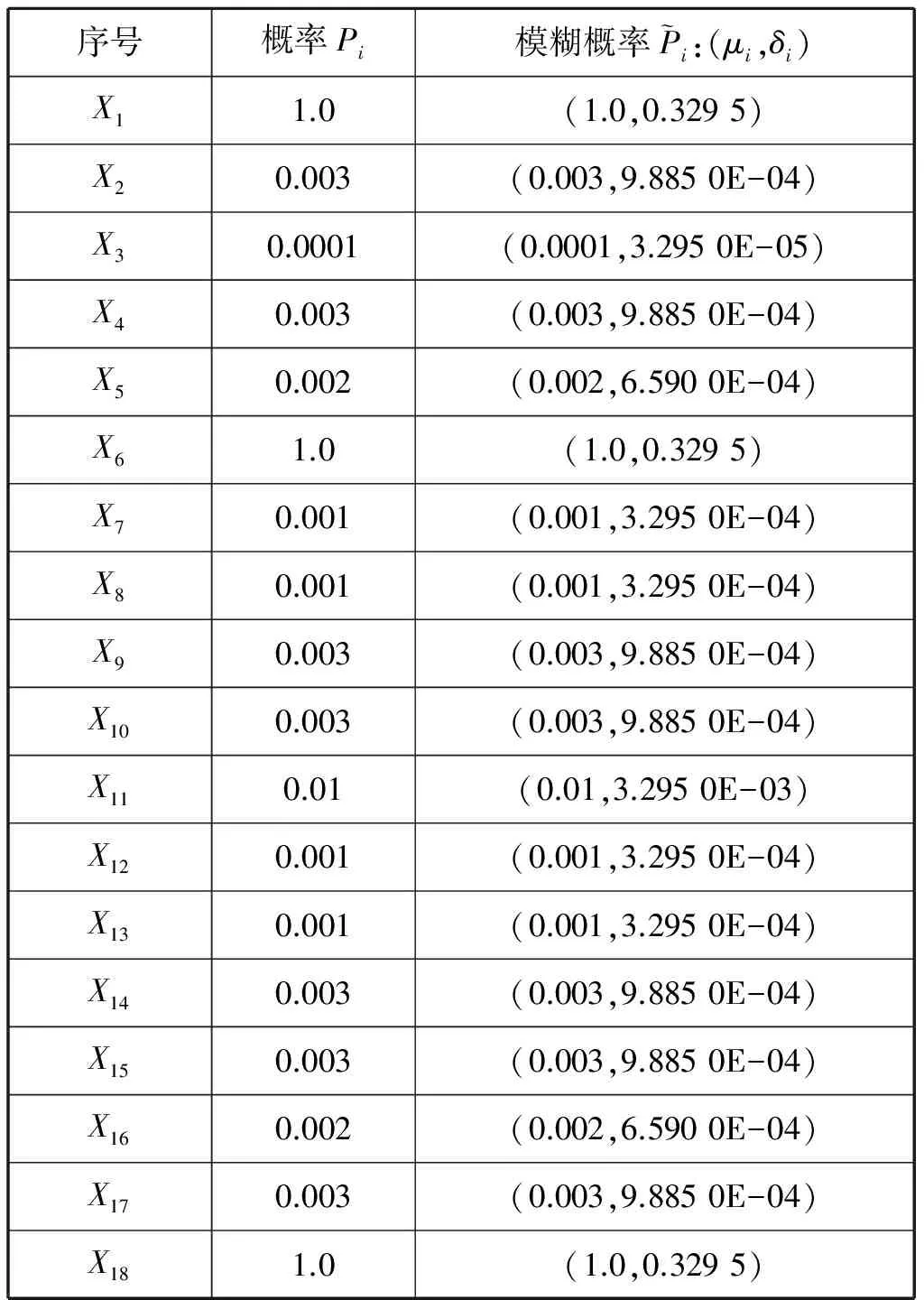
表2 底事件概率

然后，计算出顶事件的模糊概率为

2.4计算底事件结构概率重要度和模糊重要度

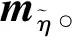
e={4.844 26×10-6，3.229 51×10-6，6.459 02×

10-6，9.688 53×10-5，0.000 21，0.516 72，

0.016 15，0.016 15，0.048 44，0.048 44，

0.007 30，0.000 49，0.000 49，0.001 46，

0.146 06，0.000 39，0.000 59，0.197}

0.001 10，0.722 19，0.090 27，0.090 27，

0.270 82，0.270 82，0.004 54，0.000 91，

0.000 91，0.002 72，0.272 18，0.000 56，

0.000 83，0.275 33}

X0={0.004 86，0.004 86，0.000 16，0.004 86，

0.009 89，6.483 23，0.810 40，0.810 40,

2.431 21，2.431 21，0.040 72，0.008 15，

0.008 15,0.024 43，2.443 37，0.004 94，

0.007 41，2.471 73}

2.5确定参考序列和比较序列

2.6计算灰色模糊关联度系数和关联度

根据式(9)计算比较序列与参考序列的绝对差值Δik(篇幅有限，不具体列出)，并由式(10)和式(11)分别得出：Δmin=0.000 162；Δmax=6.483 230；Δv=1.051 442；θv=0.162 179。由此可知Δmax>3Δv，θv≤ρ≤1.5θΔ，即0.162 179≤ρ≤0.243 268，则ρ取0.2。

将上述各值代入式(8)计算各比较序列的灰色关联系数rik，并结合各底事件的权重序列e，根据式(12)加权计算出各个最小割集的灰色关联度为：r={0.268 37，0.268 37，0.268 79，0.285 79，0.285 79，0.287 81，0.287 81，0.265 67，0.265 59，0.290 33，0.265 670，0.265 59，0.290 33，0.265 28，0.265 19，0.289 94，0.287 24，0.287 16，0.311 90}

2.7结论分析

与参考序列关联度较大的几个最小割集的关联度排序情况为：T19>T10=T13>T16=T17>T7=T6>T17=T18>T4=T5。该排序表明这些最小割集所代表的故障模式对船舶操纵性搁浅事故发生的影响较大，在系统分析和风险管理中应特别注意，也可据此制定相应的风险控制措施，以提高事故预防的效果。以最小割集T19为例：T19={X15，X18}表示由于“没有合理利用有效的信息”和“检测环境较差”而造成驾驶员没能检测出船舶航行中的错误和误差，从而使船舶偏离了安全的航道，导致船舶操纵性搁浅。该故障模式对最终船舶搁浅事故的发生影响较大。

此外，从这些对顶事件发生影响较大的几个最小割集的组成情况来看，出现频率较大的底事件为X18，X6，X11，X15和X9。而模糊重要度值较大的几个底事件的重要度排序情况为：X6>X18>X15>X9=X10>X7=X8。综合起来看，X6，X18，X15和X9的模糊重要度较大且在与顶事件关联度较大的最小割集中出现的频率也较高，对顶事件发生的影响较大。此外，X11的模糊重要度值虽然不高，但是容易与其他底事件结合而形成对顶事件影响较大的故障模式(T10，T13，T16)，因此其对顶事件的影响也较大，且反映了船长在整个安全航行中的重要职责与关键作用，应予以着重考虑。

综上，通过对船舶操纵性搁浅模糊故障树的灰色模糊关联进行分析可知，为降低船舶搁浅事故发生的概率，可着重控制T19，T10和T13等与船舶搁浅事故关联较大的故障模式及X6，X18，X11，X15和X9等事件的发生。例如：合理利用有效的信息提高检测水平，降低环境因素对检测结果准确度的干扰，保证船舶驾驶员能及时发现航行误差;船长充分发挥其在安全航行保障工作中的重要作用，认真履行职责，对驾驶员的操作予以及时的监督和确认，保证船舶安全航行。

3 结束语

将灰色模糊关联方法应用于船舶搁浅模糊故障树的分析中，能在基本事件失效概率具有不确定性的情况下对故障树进行定性和定量分析，同样能找出对顶事件发生影响较大的底事件和故障模式，且思路清晰、便于操作，可为降低船舶操纵性搁浅事故概率发生提供理论参考依据。

[1] 中华人民共和国海事局. 2012水上交通事故年报[R]. 2012.

[2] 陈刚，张圣坤. 船舶搁浅概率的模糊事件树分析[J]. 上海交通大学学报, 2002,36(1):112-116.

[3] 李典庆，唐文勇，张圣坤. 船舶驾驶失效搁浅概率的混合事件树分析[J]. 上海交通大学学报，2003,37(8):1146-1150.

[4] 赵艳萍，贡文伟. 模糊故障树分析及其应用研究[J]. 中国安全科学学报，2001,11(6)：31-35.

[5] 华小洋，胡宗武，范祖尧. 模糊故障树分析方法[J]. 机械强度，1998,20(1)：35-40.

[6] 周真，马德仲，于晓洋，等. 模糊灰关联分析方法在故障树分析中的应用[J]. 电机与控制学报，2012,16(3)：60-64.

[7] 吕锋. 灰色系统关联度之分辨系数的研究[J]. 系统工程理论与实践，1997(6):49-54.

[8] AMROZOWICZ M, BROWN A J, GOLAY M. A Probabilistic Analysis of Tanker Groundings[C]. 7th International Offshore and Polar Engineering Conference, Honolulu, Hawaii, 1997.

[9] AMROZOWICZ M D. The Quantitative Risk of Oil Tanker Groundings[D]. Massachusetts: Department of Ocean Engineering, Massachusetts Institute of Technology, 1996.

[10] 张则谅. 船舶搁浅触礁事故原因的分析[J]. 上海海运学院学报，1982,3(2)：1-12.

[11] 张则谅. 船舶搁浅触礁事故的分析及其预防途径[J]. 中国航海，1982(2)：49-62.

[12] 李东宁，朱怀伟，郑中义. 船舶搁浅致因分析研究[J]. 交通世界:建养·机械，2009(6)：276-279.

[13] 陈伟炯. 船舶搁浅、触礁事故的原因及预防[J]. 天津航海，1998(2)：1-2.

[14] SWAIN A D, GUTTMANN H E. Handbook of Human Probability Analysis with Emphasis on Nuclear Power Plant Applications-Final Report [R]. Washington D C: U.S. Nuclear Regulatory Commission, 1983.

GreyFuzzyRelationalAnalysisforFuzzyFaultTreeofShipGrounding

CHENTingting,SHIChaojian,LEIQin
(Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)

The fuzzy fault tree of ship powered grounding is established by introducing normal fuzzy numbers to represent the probabilities of each basic event and the top event. The grey fuzzy relational method is introduced to analyze the fault tree both qualitatively and quantitatively. The structure function and the minimal cut sets of the tree are obtained. And the structure-probability importance degree and the fuzzy significance of each basic event are also calculated. The fuzzy significance set of the basic event is taken as a reference sequence, while the structure-probability importance degree is considered as the weight set in the grey relational model. Then, the relational degrees between each fault mode and the top event are obtained. The higher relational degree, the stronger influence to the top event happening. Finally, the basic event which may greatly influence the top event happening is identified based on comprehensive analysis. The results can provide some references and basis for reducing the probability of ship powered grounding.

waterway transportation; grey fuzzy relational; fuzzy fault tree; normal fuzzy number; fuzzy significance; structure-probability importance degree; ship grounding

2015-05-12

陈婷婷(1987—)，女，安徽淮北人，博士生，主要研究方向为智能航海理论与船舶交通安全等。E-mail：luckytting@163.com

1000-4653(2015)03-0083-06

U698.6

A