输电线路碳纤维复合材料芯加速蠕变试验研究*

兰逢涛，陈 新，杨 青，杨长龙

(1 国网智能电网研究院，北京100192;2 辽宁省电力有限公司沈阳供电公司，辽宁沈阳100300)

碳纤维复合芯导线是由高导电软铝线绞制在碳纤维复合芯上制成，该新型导线具有高强、轻质和低垂度等显著特点，是一种节能、环保型导线，在高压架空导线上有广泛应用前景［1－3］。其中，碳纤维复合芯是该导线的关键承载部件，其由单向增强碳纤维/玻璃纤维和粘性环氧树脂基体经拉挤工艺制成，复合芯的综合性能决定了导线安全使用性［4］。

碳纤维复合材料具有高比强度、高比刚度以及耐疲劳、耐腐蚀等特性［5－7］，正是由于这些优异的性能使得碳纤维复合材料服役时间长，碳纤维复合材料在长期载荷作用下的蠕变行为将是影响其使用寿命及结构安全性的决定性因素。由于输电线用碳纤维复合材料强度高、服役时间长，而自然环境试验周期长、费用高，所以有必要通过短期加速试验预测长期老化性能，并建立相关预测模型评估其服役寿命。

国内外学者对纤维复合材料蠕变行为开展了大量工作，主要集中在蠕变的关键影响因素及蠕变与材料性能之间关系两个方面。向小运等［8］开展了复合材料蠕变本构关系研究并通过实验测定了相关参数和碳纤维树脂基复合材料蠕变的温湿等效模型。Gupta 等［9］研究了树脂基织物复合材料在轴向和偏轴载荷作用下的蠕变行为。Nedjar［10］模拟了单向纤维复合材料在长期蠕变载荷作用下的开裂行为。

碳纤维复合材料的蠕变行为受到了国内外学者的广泛关注，然而对于输电线用碳纤维复合材料芯蠕变行为研究的报道较少。本文以输电线用碳纤维芯棒为研究对象，分析了温度和应力加速对碳纤维复合材料蠕变行为的影响，试验研究了不同温度和应力下碳纤维复合材料芯棒的蠕变应变演化，研究结果将为碳纤维复合材料在输电线领域的应用提供试验方法及实践经验。

1 试验概况

碳纤维复合芯杆试件由国网智能电网研究院提供。如图1，杆件直径8.65mm，其内层为碳纤维复合材料，外层为玻璃纤维复合材料。

图1 试件Fig.1 Test specimen

如图2 所示，蠕变试验在Instron 疲劳试验机上进行。蠕变试验温度为160℃、140℃和125℃，由于碳纤维复合芯强度为2000MPa，蠕变应力水平分别取强度值的90%、50% 和使用应力，即应力取1800MPa、1000MPa 和500MPa。

图2 蠕变试验装置Fig.2 The apparatus of the creep test

2 试验结果及分析

2.1 以时间－温度移位因子构建蠕变主曲线

图3 为500MPa、1000MPa 和1800MPa 下不同温度和应力对应的蠕变应变曲线。对比图中同温度下不同应力的蠕变曲线可以看出，三种应力水平下对应的蠕变曲线不重合。因此碳纤维复合芯的蠕变行为是非线性的。同时，蠕变速率随温度和应力水平增加而增大。

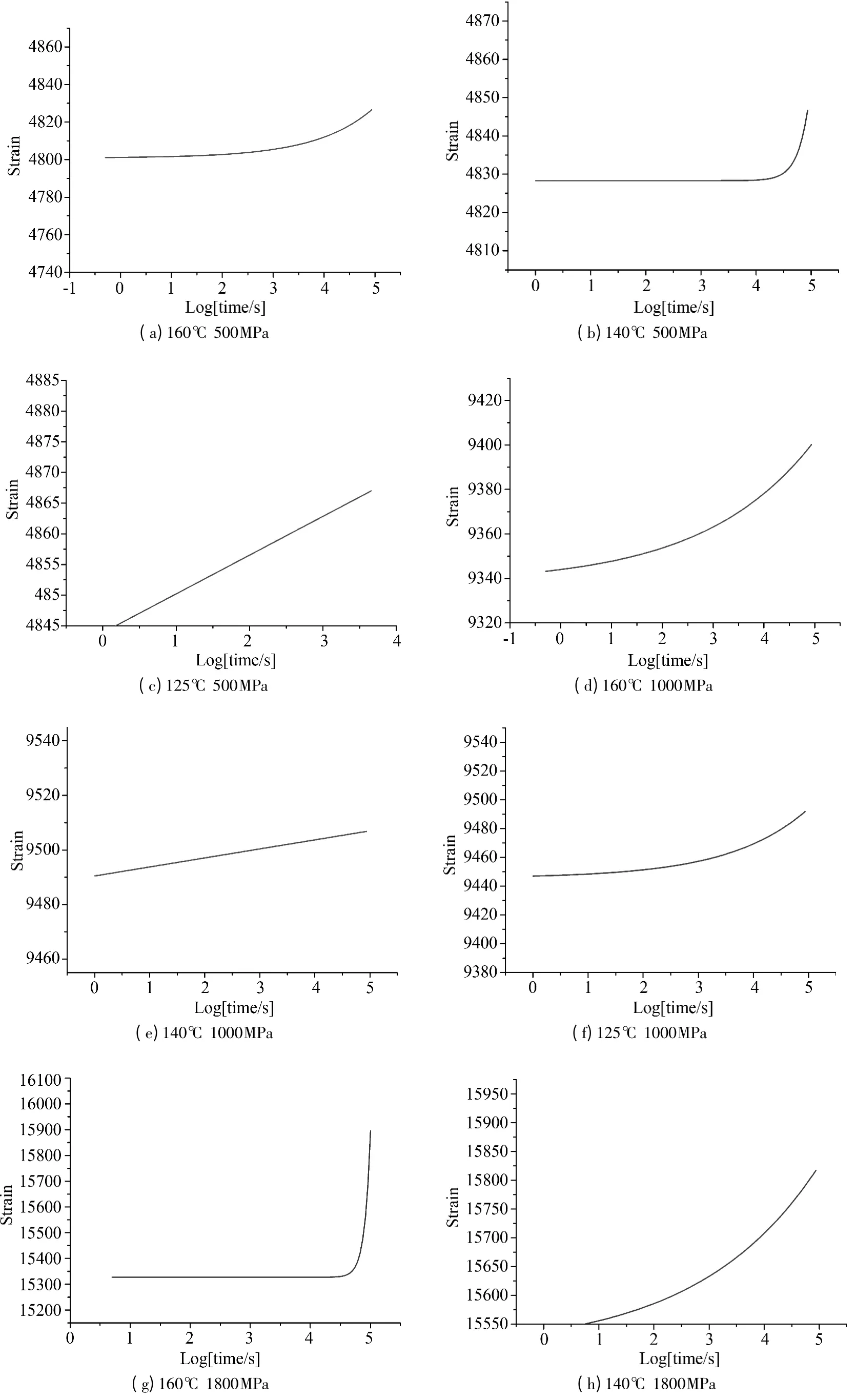
图3 蠕变应变曲线Fig.3 The curve of creep-strain

根据时间－温度等效原理，黏弹性材料高温下短时间的力学性能与低温下长时间的力学性能相当，即温度的升高相当于时间标尺的缩短。这种等效性可以通过对数坐标轴的平移来实现。蠕变柔量函数可表示为:

取T=125℃为参考温度，将图3 中其它温度下的蠕变应变－对数时间曲线向参考曲线作水平移位，移位的距离就是相应的温度移位因子。利用MathCAD 程序计算移位曲线与参考曲线之间的最佳移位距离，计算结果为移位因子，所得蠕变应变主曲线如图4 所示，移位因子见表1。

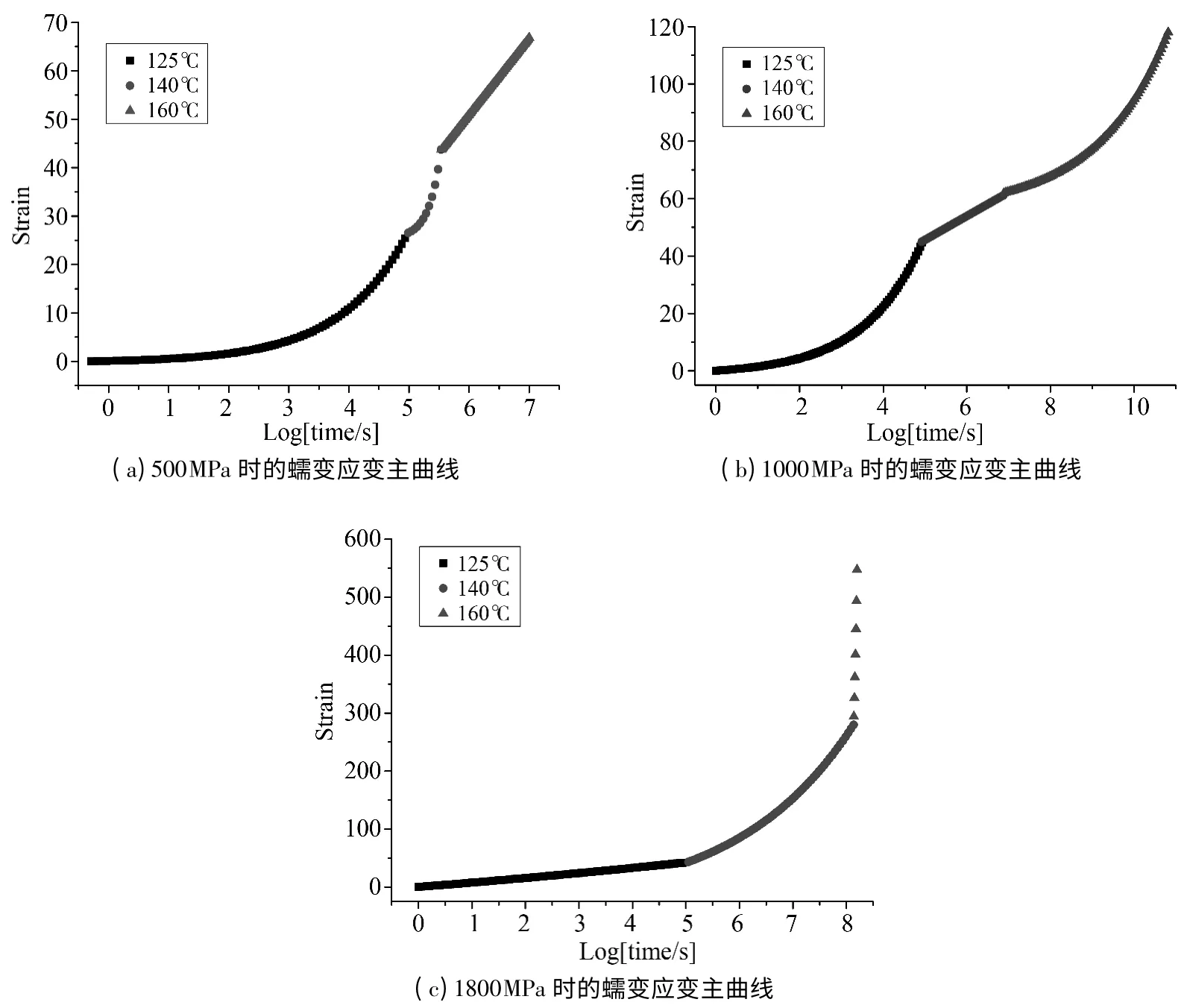
图4 不同应力蠕变应变主曲线Fig.4 The curve of creep-strain under different stress conditions

表1 不同应力下的时间-温度移位因子logTable 1 The shifted divisor，log，of time-temperature under different stress conditions

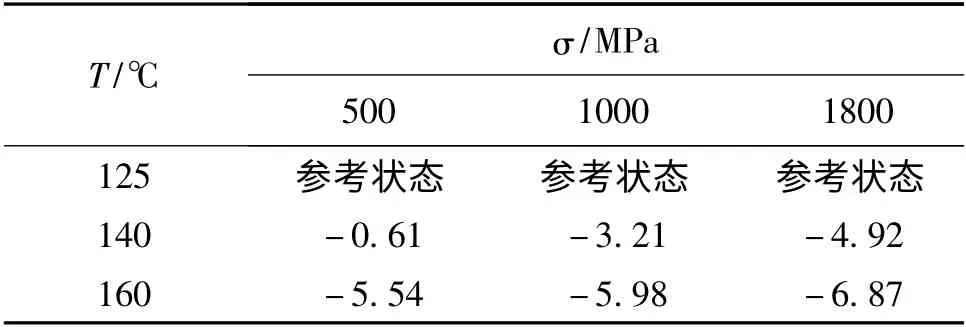
表1 不同应力下的时间-温度移位因子logTable 1 The shifted divisor，log，of time-temperature under different stress conditions

T/℃ σ/MPa 500 1000 1800 125参考状态 参考状态 参考状态140 －0.61 －3.21 －4.92 160 －5.54 －5.98 －6.87

此外，从表1 可知，以125℃为参考温度，500MPa、1000MPa 和1800MPa 下160℃对应的温度移位因子分别为－5.98 和= －6.87，可见不同应力下的温度移位因子是不同的，这与时间－温度－应力等效原理的结果一致。同时，主曲线的时间跨度比试验所经历的时间(108s)显著增大，例如，1800MPa 下的蠕变柔量主曲线的时间跨度达到5.14年(1.62 × 108s)。也就是说，依据时间－温度等效原理，1800MPa 的应力作用下，对应于160℃的短期(86400s)蠕变应变和蠕变柔量测试数据，可以用来预估125℃时长达5.14年的蠕变性能。因此，时间－温度等效原理提供了一种材料长期力学性能的加速表征方法。

2.2 以时间－应力移位因子构建蠕变主曲线

根据时间－应力等效原理，黏弹性材料高应力下短时间的力学性能与低应力下长时间的力学性能相当，即应力的增加相当于时间标尺的缩短。这种等效性可以通过对数坐标轴的平移来实现。蠕变柔量函数可表示为:

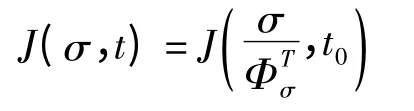
取σ =500MPa 为参考应力，将图3 中其它应力下的蠕变应变－ 对数时间曲线向参考曲线作垂直移位，移位的距离就是相应的应力移位因子。利用MathCAD 程序计算移位曲线与参考曲线之间的最佳移位距离，计算结果为移位因子，所得蠕变应变主曲线如图5 所示，移位因子见表2。

图5 不同温度蠕变应变主曲线Fig.5 The curve of creep-strain under different temperature conditions

表2 不同温度下的时间-应力移位因子Table 2 The shifted divisor，of timestress under different temperature conditions

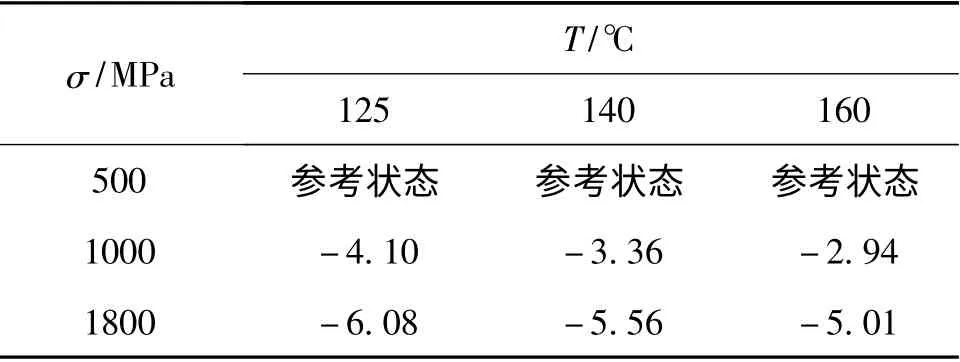
表2 不同温度下的时间-应力移位因子Table 2 The shifted divisor，of timestress under different temperature conditions

σ/MPa T/℃125 140 160 500参考状态 参考状态 参考状态1000 －4.10 －3.36 －2.94 1800 －6.08 －5.56 －5.01

此外，从表2 可知，以500MPa 为参考应力，125℃、140℃和160℃下1800MPa 对应的应力移位因子分别为= －5.56和= －5.01，可见不同温度下的应力移位因子是不同的，这与时间－温度－应力等效原理的结果一致。同时，主曲线的时间跨度比试验所经历的时间(8.13 ×106s)显著增大，例如，160℃下的蠕变柔量主曲线的时间跨度达到94 天(8.13 ×106s)。也就是说，依据时间－ 应力等效原理，160℃的温度作用下，对应于1800MPa 的短期(86400s)蠕变应变和蠕变柔量测试数据，可以用来预估500MPa 时长达94 天的蠕变性能。因此，时间－应力等效原理提供了一种材料长期力学性能的加速表征方法。

2.3 碳纤维复合芯棒长期蠕变性能预测

图6 为通过125℃、140℃和160℃预测所得50℃时的蠕变应变曲线，由图可见，三种温度下的平移后曲线前期较为吻合，而后期140℃和160℃平移后所得50℃时的蠕变应变曲线较为吻合，而125℃平移所得差异较大，这主要是由于125℃时500MPa下的蠕变应变较小，其主曲线未能反应出蠕变实际过程，而仅仅是线性段，因此在后期非线性段产生较大误差。

由图6 中50℃时500MPa 下的应变主曲线可以预测1年(约107.5s)的蠕变应变量分别约为30.7με(由125℃预测)、20.3με(由140℃预测)和10.2με(由160℃预测)，即1km 长碳纤维复合芯导线1年由于蠕变伸长量为30.7mm、20.3mm 和10.2mm;而20年(约108.8s)的蠕变应变量约50.8με、50.1με和36.6με，即1km 长碳纤维复合芯导线20年由于蠕变伸长量为50.8mm、50.1mm 和36.6mm;30年(约109s)的蠕变应变量约56.4με、59.7με 和54.3με，即1km 长碳纤维复合芯导线30年由于蠕变伸长量为56.4mm、59.7mm 和54.3mm。

图6 50℃时500MPa 蠕变性能预测Fig.6 The creep behavior of the ACCC conductor at 50℃and 500MPa

3 结论

在不同温度和应力水平下对碳纤维复合芯进行了短期蠕变测试，分析了应力对碳纤维复合芯蠕变行为时间－温度等效性的影响。在不同温度和应力水平下对碳纤维复合芯进行了短期蠕变测试，基于时间－温度－应力等效原理，采用两种不同顺序的分步移位方案对碳纤维复合芯的长期蠕变性能进行加速表征。并给出相应的移位因子和加速表征所能预测的时间尺度。研究结果验证了时间－温度－应力等效原理关于分步移位表述的可行性。与时间－温度等效原理和时间－ 应力等效原理相比，时间－温度－应力等效原理更有优势作为碳纤维复合芯长期黏弹性能的加速表征方法。

［1］张国光. 碳纤维复合芯导线在电力传输线路上的应用［J］. 山西电力，2008(02):45 －46.

［2］何州文，陈新，王秋玲，等. 国内碳纤维复合芯导线的研究和应用综述［J］. 电力建设，2010(04):95 －98.

［3］刘辉，陈新，王英男. 耐高温碳纤维复合芯基体树脂研究［J］. 玻璃钢/复合材料，2013(03):23 －26.

［4］A Alawar，J Bosze，R Nutt. A composite core conductor for low sag at high temperatures［J］. IEEE Transaction of Power Delivery，2005，20:2193 －2199.

［5］W Hao，X Yao，Y Ma，et al. Experimental study on interaction between matrix crack and fiber bundles using optical caustic method. Eng Fract Mech. 134 (2015)，354 －367.

［6］W Hao，Y Yuan，X Yao，et al. Computational analysis of fatigue behavior of 3D 4-directional braided composites based on unit cell approach［J］. Adv Eng Softw，2015，82:38 －52.

［7］W Hao，C Tang，Y Yuan，et al. Experimental study on the fiber pull-out of composites using digital gradient sensing technique［J］. Polym Test，2015，41:239 －244.

［8］向小运，张双寅. 复合材料蠕变本构关系及实验测定Ⅰ. 本构关系［J］. 复合材料学报，1992(02):31 －37.

［9］A Gupta，J Raghavan. Creep of plain weave polymer matrix composites under on-axis and off-axis loading［J］. Composites Part A:Applied Science and Manufacturing，2010，41(9):1289 －1300.

［10］B Nedjar. Modeling long-term creep rupture by debonding in unidirectional fibre-reinforced composites［J］. Int J Solids Struct，2014，51(10):1962 －1969.