基于贝叶斯网络的列车运行图稳定性评价

王金霞，孟学雷，刘 健

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

1 概述

在铁路运输组织领域，对列车运行图稳定性的评价是一个相对较新的研究课题，国内外学者的研究主要集中在列车运行图的可靠性、鲁棒性、均衡性、可调整弹性和动态性能指标等方面。不同研究者对于列车运行图稳定性的影响因素研究侧重点各不相同，但关于稳定性尚没有统一的定量描述。杨肇夏等[1]对列车运行图动态性能指标进行研究；彭其渊等[2]对“均衡性”和“可调整弹性”的研究，为日后列车运行图稳定性分析和优化思想的形成奠定基础；De Kort A F 等[3]将列车运行图的稳定性作为列车运行图能力的一部分，提出运行图运输能力的评价模型方法；王京广[4]针对货物列车的不均衡性到发时刻进行统计；Goverde R M P[5]运用极大加代数方法描述周期运行图，提出其稳定性的评价方法；李成兵等[6]研究列车运行图的均衡性，提出高质量的运行图编制技术；陈军华等[7]将列车运行图的抗干扰能力、可调整性、自我恢复能力纳入稳定性的范畴，并且将列车运行图稳定性概括为可靠性、鲁棒性、稳定性 3个方面；Meng Xuelei 等[8]从铁路路网角度研究列车运行图的稳定性，构建双层优化模型，对路网上列车运行图稳定性做出新的定义，随后又提出使用信息熵理论评估列车运行图稳定性。这些文献对列车运行图稳定性的评价研究具有重要的借鉴意义。

列车运行图稳定与否，直接影响铁路运输效率和旅客运输服务质量，而且天气、调度人员指挥、突发事件等影响因素之间关系具有不确定性。近年来，随着科技进步发展起来的贝叶斯网络能够较好地弥补传统方法对稳定性评判的不足，贝叶斯网络是以概率论为基础知识的图模型，使用概率表示不确定性。贝叶斯网络现已广泛应用至高层建筑火灾后果预测、列控系统安全风险评估、铁路危险货物运输安全评估[9]、旅客列车晚点等领域，表明其在工程计算领域具有广泛的适应性。因此，将贝叶斯网络的理论方法应用于列车运行图稳定性研究。

2 列车运行图稳定性影响因素分析

评价铁路在遇到突发事件时的列车运行图稳定性，首先应分析运行过程中可能影响列车运行图稳定性的因素。通常情况下，铁路行车按照图定时刻表运行，图定时刻表的质量决定铁路服务质量，它确定铁路线路、站场、机车车辆等设备的运用，通过列车运行图将整个铁路网的运输生产活动联系为一个整体，是铁路运输生产计划的综合体现。

2.1 影响列车运行图稳定性的内部因素

通过分析，将影响列车运行图稳定性的内部因素整理为以下 9个方面。

（1）铁路线路级别。等级越高、运输能力越大，列车运行图的稳定性越高。

（2）闭塞系统类型。目前主要有半自动闭塞、自动闭塞和移动闭塞 3种系统。不同闭塞系统所允许的最小追踪间隔时间不同，移动闭塞系统具有最大的运输能力，有利于路网运行图长远的稳定性。

（3）车站联锁类型。目前电气联锁和计算机联锁系统均在我国铁路使用。联锁系统的响应速度是影响车站接发列车能力的关键因素，更深层次的因素还包括通信能力、计算能力、可靠性和容错能力。

（4）机车牵引性能。在一定程度上机车牵引能力决定列车速度，进而影响列车在区段内的运行时间。因此，机车牵引性能也是影响区间能力的因素。

（5）区间里程。区间里程数大小影响列车的运行时间，从而影响列车运行图的稳定性。

（6）区段容量负荷。每个区段的容量负荷是1d内图定通过的列车数量与区间通过能力的比值。如果负荷过重，则当列车运行受到干扰时很难重新调度安排，列车恢复按图行车的希望渺茫。

（7）车站容量负荷。车站容量负荷是1d 中图定列车到达和离开车站的数量与车站接发列车能力的比值。车站容量负荷越大，列车运行图稳定性越小。

（8）总附加时分。总附加时分是每一列车在每个区段运行缓冲时间的总和。在列车受到干扰时，缓冲时间能抵消一些轻微的列车晚点，从而应对列车运行过程中的扰动。总附加时分越长，列车运行图稳定性越强。

（9）总停站缓冲时分。停站缓冲时分越多，列车运行图越稳定。列车实际运行中，很难完全按照图定的列车时刻到达、出发或通过车站，而是以规定的时刻为基点，在一定范围内波动，列车晚点也时有发生。

2.2 影响列车运行图稳定性的外部因素

列车运行图稳定性的外部影响因素从3个方面进行分析。

（1）人员操作导致的时间偏差。在影响列车调度的运输组织人员操作中，主要包括列车调度员、助理调度员、车站值班员和车站调度员的作业。

（2）设备故障率。移动设备和固定设备发生故障的概率会影响列车运行图的稳定性。

（3）环境。环境主要包括事故灾难(交通事故、火灾爆炸、列车脱轨等)、气候(如冰雨暴雪、温度变化等) 和自然灾害(如冰雨暴雪、地震、滑坡、泥石流、风灾等)。

3 基于贝叶斯网络理论的列车运行图稳定性评价

采用贝叶斯网络分析列车运行图稳定性时，根据各因素之间相互影响的关系，建立事件树模型，在树形图中，将稳定性作为顶事件，其他能够直接或间接影响稳定性的因素作为事件树的基本事件，部分因素作为中间事件，运用逻辑门符号描述系统中各事件之间的因果关系。在事件树模型构建基础上，通过基本事件、逻辑门与节点间的映射关系得到贝叶斯网络，根据逻辑门与条件概率的对应关系标定概率。

3.1 贝叶斯网络基础理论

贝叶斯网络是基于概率推理的有向无环图( Directed Acyclic Graph，DAG)，由代表变量的节点和连接这些节点的有向边组成。每一个节点均标注定量的概率信息，有向边代表变量之间的因果关系，用 J = { G，V，E，P } 表示，其中 V 为有限个变量集合，G 为变量域的 DAG，E 为有向边集合，P 为条件概率的分布集合。构建贝叶斯网络主要分 2个步骤进行：定性描述(变量的定义) 和定量描述(即贝叶斯网络结构和参数)。贝叶斯网络参数是反映变量之间关联性的局部概率分布集(参数)，称为条件概率表。概率值表示子节点与其父节点之间的关联强度。

（1）先验概率。设 X1，X2，…，Xn为样本空间 S 中的事件，P(Xi) 可以根据以前的数据分析得到，则称为先验概率。先验概率是根据历史资料或主观判断所确定的各事件发生的概率。

（2）后验概率。设 X1，X2，…，Xn为样本空间 S 中的事件，则在事件 Xi发生情况下，Xj发生的概率 P(Xj| Xi) 称为后验概率。将 X1作为根节点，赋予先验概率 P(X1)。若 X1与 X2有关，从X1到 X2建立一个联结，用 P(X2| X1) 表示联结度；若 X1与 X2无关，则赋予先验概率 P(X2)。

在第 i 级，假设 Xi节点的父节点集合为其中Xi与 { X1，…，Xi，…，Xn} 中的其他变量独立，即

当∏(Xi)=Φ时，P(Xi|∏(Xi)) = P(Xi)。

3.2 列车运行图稳定性的事件树模型

根据前文对影响因素的分析，确定构建事件树的基本元素，列车运行图稳定性除了考虑内部影响因素之外，还要考虑人员、设备和环境等外部影响因素。例如：以 3种闭塞系统类型和稳定性作为基本事件，因子及逻辑关系如图1 所示。

图1 因子及逻辑关系

因此，可以依次得到其他基本因素各自对应的事件树。基于铁路运输组织领域有关专家的分析研究，文中事件树模型的影响因子由 21个基本事件、7个中间事件和 1个顶事件组成。各事件的编号和名称如表1 所示。列车运行图稳定性评估事件树模型如图2 所示。

3.3 事件树的贝叶斯网络映射

根据贝叶斯网络的描述，事件树模型向贝叶斯网络映射时，贝叶斯网络的节点与事件、逻辑门与连接强度对应。贝叶斯网络的连接强度根据逻辑关系可以列出其条件概率表，并且将其转换成数学表达式用于后续的概率分布计算。与门映射如图3 所示，或门映射如图4 所示。

令 Xi= 1 时表示列车运行图的稳定性受到影响，令 Xi= 0 时表示列车运行图的稳定性没有受到影响，则与门逻辑的条件概率分布公式为

或门逻辑的条件概率分布公式为

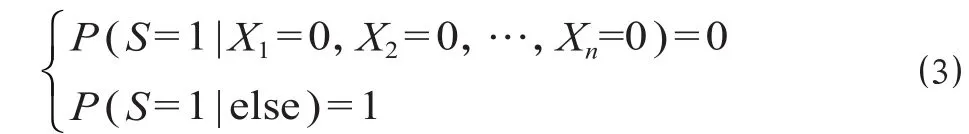
根据上述映射方法，将图2 的事件树映射为对应的贝叶斯网络，如图5 所示。

表1 各事件的编号和名称

图2 列车运行图稳定性评估事件树模型

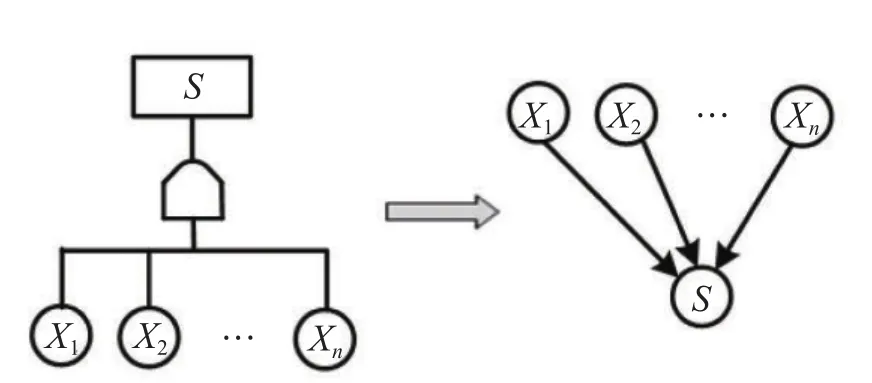
图3 与门映射

图4 或门映射

3.4 基本事件概率的标定方法

确定影响因素后，定量分析列车运行图稳定性时，首先需要确定基本事件的先验概率。由于列车运行中突发情况等不确定性因素，造成基本事件在遇到突发情况前后在不同状态存在不稳定性，标定概率时需要考虑这种模糊性，以确保先验概率尽可能准确，运用德尔菲法改进标定基本事件的先验概率。

采用改进后的德尔菲法标定事件基本概率时，运用梯形模糊数代替评价的尺度，计算结果较为严谨，克服指定概率不精确的问题。在确定不同影响因素的重要程度时，从1—9 共 9个数字中选择评价尺度。

（1）单个因素先验概率标定。首先获取专家评分向量 A =(a1，a2，…，an)，其中 n 为参与评分的专家数，然后计算得到先验概率值为

（2）多个因素先验概率标定。如果因素 Xi比 Xj发生的概率更大时，则专家评分取值相比较高，从而得到评分矩阵为

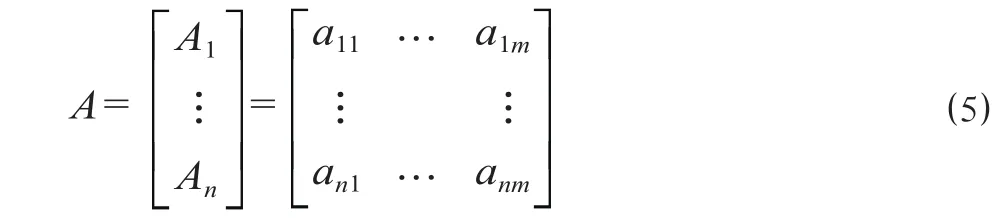
以 aij表示矩阵 A 中第 i个元素相对于第j个元素的影响力，令

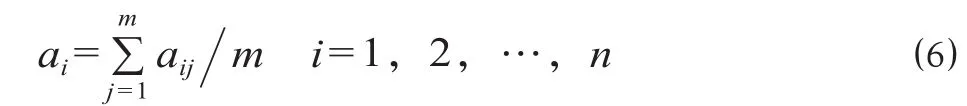
得到先验概率向量为

通过公式⑺得到权值 Wi，将该值作为基本事件Ai的先验概率值，再利用公式⑵( 如果是或门逻辑则根据公式⑶) 运用逐层递增的方法依次计算其父节点的概率分布。直至得到顶事件的概率分布，获得后验概率值。

3.5 基于贝叶斯网络的概率计算

用分层递进的方法，从基本事件节点开始逐级向上，计算得到顶事件的概率值，然后依据此概率值，判定列车运行图的稳定性等级。具体而言，分 2种情况。

（1）与门结构的概率计算。如图3 所示，在已知基本事件 X1，X2，…，Xn概率的条件下，根据公式⑵可以得到事件 S 的条件概率计算公式为

（2）或门结构的概率计算。如图4 所示，在已知基本事件 X1，X2，…，Xn概率的条件下，根据公式⑶可以得到事件 S 的条件概率计算公式为

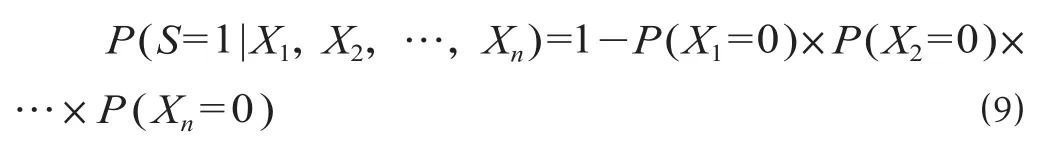
令集合 V 为稳定性的评语级，V ={ V1，V2，V3} = { 很稳定，较稳定，不稳定 }，其中 [ 0.90，1 ]为很稳定，[ 0.80，0.90) 为较稳定，[ 0，0.80) 为不稳定。至此，可以根据已经得到的概率值评判该列车运行图稳定性级别，因突发事件导致列车运行图稳定性改变时，及时找出关键影响因素，确定可行的运行调整措施，为运输组织决策提供参考，根据实时情况调整列车运行图，确保列车良好的运行秩序。

图5 列车运行图稳定性贝叶斯网络

4 算例分析

以沪宁城际高速铁路(上海虹桥—南京) 为例，区段采用移动闭塞设备，计算机联锁系统，运营里程 301km，实际运行速度最高 300km/h，机车采用动力分布式电力动车组 CRH3 型。按照列车开行方案，上海与南京之间每天计划安排高速列车120 对，其中时速 300～350km本线高速列车开行 98 对/d，占 81.67%，时速 200～250km跨线列车 22 对/d，占 18.33%，高峰时段最小发车间隔5min。全线共设 21个站，平均 15km即有 1个站，最小行车间隔时间 3min。假设遇到雨雪天气，需要降速行驶，则列车运行图稳定性概率值会出现新的变化。

4.1 初始列车运行图稳定性概率值

依据图5，按照前述方法确定基本事件的先验概率值。以闭塞类型因素为例确定各个闭塞概率取值为节点的先验概率，首先得到专家评分矩阵。

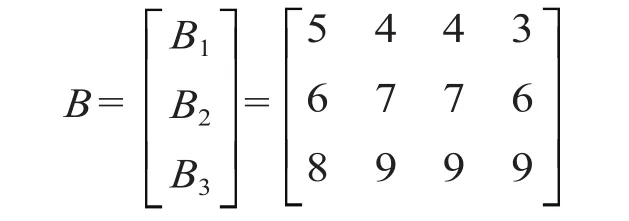
再根据公式⑷至公式⑸得到

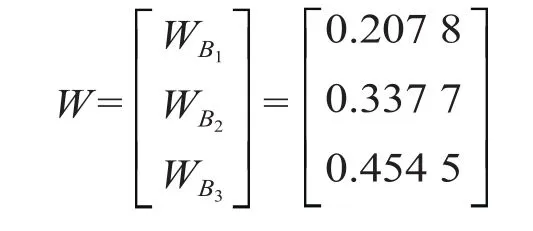
因此，各个闭塞类型的先验概率为 P(B1=1) =0.2078，P(B2=1) = 0.3377，P(B3=1)=0.4545。同理可求出其他各基本事件的先验概率，计算结果如表2 所示。

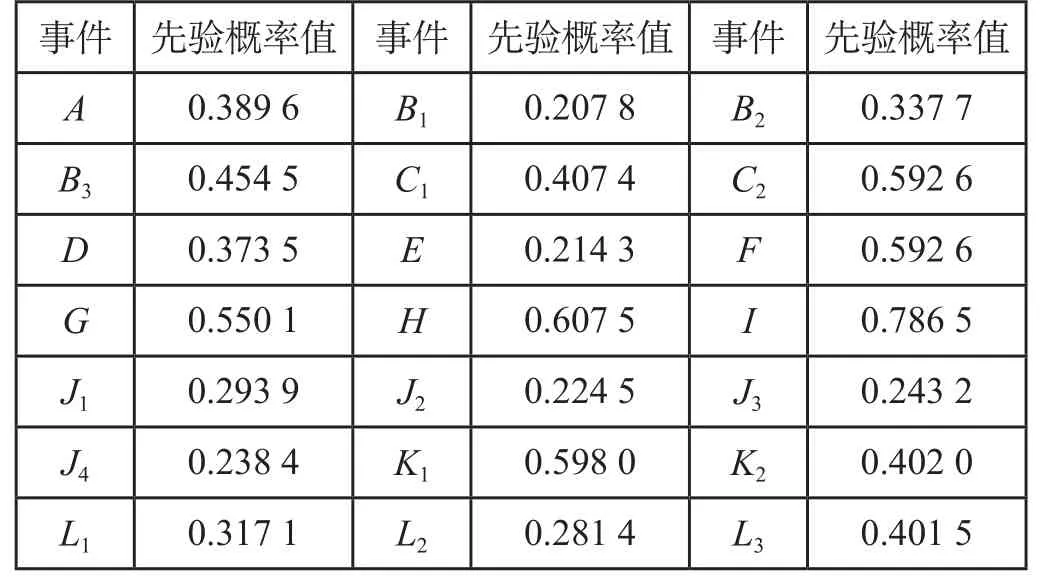
表2 先验概率表

标定基本事件的先验概率后，按照公式⑶，可以得到 B 的条件概率分布为

按照公式⑼可以计算出中间事件概率为

同样可得

依照稳定性评语级可以判定列车运行图很稳定。

4.2 变化后的列车运行图稳定性概率值

假设在受到雨雪天气影响之后，列车的运行速度减缓，随着时间的推移，在车站的列车数量因无法正常运行出现滞留，总停站缓冲时分和区间运行时分等因素随之受到影响。假设变化后的先验概率表如表3 所示。

表3 变化后的先验概率表

重复前面的计算过程，得到 P(T = 1 | M1，M2) =0.956 1，稳定性概率值减少，表明列车运行图稳定性发生改变。

显然，由于天气的影响，机车的性能发挥受到限制，运行速度降低，总附加时分、总停站缓冲时分等时间增加，从而导致在车站和区间的列车数量增多，容易发生列车晚点，并且引发晚点传播的现象，如果车站的接发列车能力和区间通过能力较低，则列车运行图的稳定性较差，恢复列车按图运行的波动时间会需要更久。列车运行组织是一个非常复杂的系统，各影响因素之间并不是相互独立的。因此，一个因素的变化会引起其他诸多因素对整个系统的影响，其概率值根据影响程度将得到更新，再利用贝叶斯理论可以得到最终稳定性概率值，从而衡量影响后的稳定性。

5 结论

（1）列车运行图是铁路组织列车运行的基础，它规定各次列车占用区间的程序、区间运行时分，在车站到发和通过的时刻，当列车受到随机事件干扰时，将会发生偏离列车运行图运行的情况，高质量的列车运行图能够提供列车恢复按图运行的可能性，使列车运行图的抗干扰能力增强，而列车运行图的稳定性正是衡量这一可能性的指标。

（2）以实现列车尽量按图运行为目标，分析影响列车运行图稳定性诸多要素，用事件树模型结合与、或逻辑关系阐述各因素间相互影响的程度。

（3）基于梯形模糊数法标定基本事件先验概率值，再利用贝叶斯网络计算概率，综合考虑影响稳定性的各方面可能因素。这种定量分析稳定性的方法，在确定先验概率值后，采用条件概率公式得到顶事件后验概率值，作为稳定性评估依据。

（4）将贝叶斯网络、事件树模型应用于列车运行图稳定性评估的创新，为有效评价列车运行图稳定性提供新的思路。

[1]杨肇夏，胡安洲，李 菊，等. 列车运行图动态性能及其指标体系的研究[J]. 铁道学报，1993，15(4)：46-56.

[2]彭其渊，朱松年，阎海峰. 列车运行图可调整度评价系统研究[J]. 西南交通大学学报，1998，33(4)：367-371.

[3]De Kort A F，Heidergott B，Ayhan H. Aprobabilistic (max，+) Approach for Determining Railway Infrastructure Capacity[J]. European Journal of Operational Research，2003，148(3)：644-641.

[4]王京广. 不均衡运输对机车运用的影响及采取的措施[J]. 铁道货运，2006(10)：33-35.

[5]Goverde R M P. Railway Timetable Stability Analysis Using Max-plus System Theory[J]. Transportation Research：Part B ：Methodological，2007，41(2)：179-201.

[6]李成兵，郭倩倩，鲁工圆，等. 列车运行图的均衡性研究[J]. 铁道运输与经济，2009，31(6)：87-88，91.

[7]陈军华，张星臣，徐 彬，等. 高速铁路列车运行图稳定性及其影响因素分析[J]. 物流技术，2011，30(8)：81-84.

[8]Meng Xuelei，Jia Limin. Train Timetable Stability Evaluation based on Analysis of Interior and Exterior Factors Information Entropy[J]. Applied Mathematics & Information Sciences，2014，8(3)：1319-1325.

[9]杨能普，杨月芳，冯 伟. 基于模糊贝叶斯网络的铁路危险货物运输过程风险评估[J]. 铁道学报，2014， 36(7)：8-15.