运动学典型例题赏析
2015-11-26徐锡扬
徐锡扬

例1 下列各种情况,可以把研究对象看作质点的是
()
A.研究翻倒过程的小木块
B.讨论公转的地球
C.解释布朗运动的微粒
D.计算通过某一路标时间的列车
错解一:小木块体积小,远看可视为一点;作布朗运动的微粒体积极小,当然是质点,故选A、C.
错解二:列车做平动,车上各点运动规律相同,可视为质点,故选(D).
错因分析与解题指导:物理研究中常建立起一些理想化的模型,它是对实际问题的简化,也叫科学抽象.它撇开与当前观察无关的因素和对当前考察影响很小的次要因素,抓住与考察有关的主要因素进行研究、分析、解决问题,质点就是一个理想化的模型.错解一以为质点是指一个很小的点.但在小木块的翻倒过程中,木块各点绕一固定点转动,各点运动情况不同,不可看作质点.至于做布朗运动的微粒,尽管体积极小,仍受到来自各个方向上的液体分子(具有更小体积)的撞击,正是这种撞击作用的不平衡性使之做无规则运动,也不可把布朗运动粒子视为质点.错解二以为火车在铁道上的运动为平动,可视为质点,而本题实际考察的是经过某路标的时间,就不能不考虑它的长度,在这情况中不能视其为质点,
正解:讨论地球的公转时,地球的直径(约1.3×l04km和公转的轨道半径(约1.5×lO8km)相比要小得多,因而地球上各点相对于太阳的运动差别极小,即地球的大小和形状可以忽略不计,可把地球视为质点,故选B.
例2 关于质点的位移和路程的下列说法中正确的是
()
A.位移是矢量,位移的方向即质点运动的方向
B.路程是标量,即位移的大小
C.质点沿直线向某一方向运动,通过的路程等于位移的大小
D.物体通过的路程不等,位移可能相同
错解:A、B
正解:C、D
错因分析与解题指导:位移是表示物体位置变化的物理量,它是矢量,其方向由质点初位置指向末位置,其大小是连接质点始、末位置线段的长度.路程是指质点所通过的实际轨迹的长度,它只有大小,没有方向,是标量.
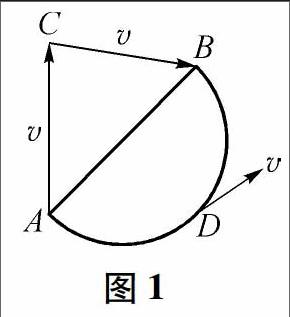
例如,如图1,质点原来在A点,经过一段时间沿轨迹ADB运动到B点,有向线段AB表示其位移,而曲线ADB的长度是路程.
不仅在曲线运动中,位移大小不等于路程,即使在直线运动中,位移的大小也不一定等于路程.如图1,物体从初位置A经过C运动到B,质点的位移是有向线段AB,而路程是AC+ CB.
事实上,只有做直线运动的质点始终向着同一个方向运动时,位移的大小才等于路程,位移的方向是由质点的始位置指向末位置的特定方向,通常它不是质点的运动方向.图中质点由始位置4分别沿折线ACB和曲线ADB运动到B点,其位移均为有向线段AB,它同质点沿路径AB的位移是相同的.而质点位于曲线上位置D时的运动方向,以及作折线运动时的运动方向均如图中v所示,其方向与位移均不相同.
例3 一个质点做初速度为零的匀加速运动,试求它在1s、2s、3s、…内的位移s1、s2、s3、…之比和在第1s、第2s、第3s、…内的位移sI、sⅡ、sⅢ、…之比.
常规解法:由初速度为零的匀加速运动的位移公式得:
解法二:利用速度图线很容易找出例题中的位移之比.如图3所示,从t=0开始,在t轴上取相等的时间间隔,并从等分点作平行于速度图线的斜线,把图线下方的面积分成许多相同的小三角形.于是,立即可得:
从t=0起,在t、2t、3t、…内位移之比为
s1:s2:s3…=1:4:9…
在第1个t、第2个t、第3个t、…内位移之比为
sI:sⅡ:sⅢ…=1:3:5:…
例4 A、B两车在一条水平直线上同向匀速行驶,B车在前,车速v2=10m/s;A车在后,车速72km/h,当A和B相距100 m时,A车用恒定的加速度a减速,求加速度a为多大时A车与B车相遇时不相撞.
分析:A车追上B车,相遇而不相撞的条件是A、B两车速度相等,从这个条件出发,作物理图景表述运动过程.
方法一:应用运动学公式求解
方法二:利用平均速度公式
方法三:利用图象求解
作v-t图象,图中画阴影线的面积值表示A车车速由20降到10m/s时,A比B多走的位移,即s1-s2=100m
方法四:选B车为参照物,用相对运动方法解,A相对于B的车速为10 m/s,A以a减速,行驶100m“停下”跟B相遇而不相撞.
方法五:用相对运动和v-t图象综合求解,即只需研究图中画阴影的三角形,三角形的竖直边为相对速度10m/s,由图可看出endprint
