基于密度划分的离群点检测算法

魏 龙，王 勇

(1.西北工业大学计算机学院，陕西 西安 710129;2.西北工业大学理学院，陕西 西安 710129)

0 引言

离群点挖掘(Outliers Mining)是数据挖掘领域中的一项重要技术，其目标是发现数据集中不同于大部分的少量数据对象，这些数据对象也被称为异常点(Abnormal Points)或孤立点(Isolated Points)。Hawkins 最早给出离群点的本质性定义:离群点是数据集中与众不同的数据，使人怀疑这些数据并非偏差，而是产生于完全不同的机制［1］。

离群点通常在数据预处理过程中被认为是噪声或异常值而清理，许多挖掘算法和任务也都试图降低离群点的影响，甚至完全排除它们。然而，由于离群点既有可能是噪声信息也有可能是有用信息［2］，随意删除孤立数据可能导致有用信息的丢失，不关注孤立数据的产生原因可能产生更多的异常情况。在诸多领域中，人们更关注与大多数据不同的特殊数据，试图挖掘隐含其中的知识和信息。例如飞机性能统计数据中的一个离群点可能意味着飞机发动机的一个设计缺陷;地理图像上的一个离群点可能标志着一个危险对象(如埋藏生化武器);网络系统中的一个离群点还可能是对某个恶意入侵的精确定位。随着研究进一步深入，离群点挖掘还可应用于信用卡欺诈、金融审计、网络监控、电子商务、故障检测、恶劣天气预报、医药研究、客户异常行为检测和职业运动员成绩分析等［3］。所以，通过离群点检测发现和利用其中有价值的信息，具有非常重要的意义。2D 密度不均匀数据点分布示意图如图1 所示。

图1 2D 密度不均匀数据点分布示意图(横坐标为二维数据X 维的值，纵坐标为Y 维的值)

迄今为止，离群点挖掘算法的研究已经取得了广泛的成果，而在基于聚类的离群点挖掘算法中，DBSCAN 算法［4］因可以聚类任意形状的簇而被广泛研究应用，现已基于这一算法的基本思路而提出了许多改进算法。第一类改进算法主要是提高算法效率:基于密度的聚类算法(CUCD)［5］，能根据数据分布计算出来虚拟的点作为核心对象，能够较好地代表数据空间，最后通过合并邻近核心对象产生聚类，但该算法对局部离群点不够敏感。张卫旭等人根据数据核心距离(使数据成为核心点的最小距离)进行排序，之后对这些数据簇类进行扫描，再按照LOF 算法判断是否为离群点［6］，该算法减少了查询的复杂度。Dongmei Ren 等人提出的算法RDF［7］，根据相对密度系数先剪枝，再进行孤立点检测，提高了效率，但准确性降低。第二类改进算法主要是优化聚类过程中的簇中心点选择:基于密度算法优化初始聚类的改进K-means 算法［8］，选择相互距离最远的K 个处于高密度区域的点作为初始聚类中心，减少了因初始聚类中心的不同而造成的误差，使得聚类更加精准;汪中等人在密度敏感的相似度量基础上设计出一种新的基于密度的初始化方法，并根据评价函数自动生成最优聚类数目［9］。第三类改进算法主要是优化混合属性对象间的相似度量:基于密度的局部离群点检测算法DLOF［10］，该方法通过引入信息熵用于确定各对象的离群属性，在计算各对象之间的距离时采用加权距离，并给离群属性较大的权重，从而提高离群点的检测的准确度。包小兵等人提出了一种基于密度的局部离群点检测算法ESLOM［11］，引入信息熵确定数据对象的离群属性，并对对象距离采用加权距离，以降低属性差异带来的误差。Breuning M M 用局部孤立系数LOF(数据点邻域的平均可达密度和数据点自身的可达密度之比)表示点的孤立程度［12］，但参数不容易确定。以上几类改进方法仍然对密度分布不均匀数据挖掘效果不理想，并且需要反复实验来选择合适的初始参数，算法均有一定的局限性和改进空间。

基于上述的考虑，本文提出基于密度划分的离群点检测算法DD-DBSCAN。

1 DD-DBSCAN 算法

1.1 离群点定义

离群点挖掘可以被形式化地描述:给出n 个数据点或对象的集合，及预期的离群点数目k，发现与剩余的数据相比差异是显著的、异常的或不一致的前k个对象［13］。在DD-DBSCAN 算法中，有2 类数据是离群点:第一类是全局离群点，即点最小距离(如1.2节定义7 所示)最大的前N 个点为离群点;第二类是局部离群点，即在其所在簇中Eps 邻域内，点的个数小于MinPts 这个阈值或者Eps 邻域内没有核心点的点为离群点。

1.2 相关概念

本节对本文所提算法用到的概念进行描述。假设P、Q 为m 维空间的任意2 个对象，有:

那么，P、Q 之间的欧几里德距离(以下简称距离)表示为:

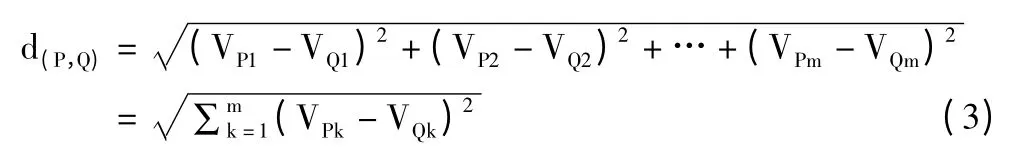
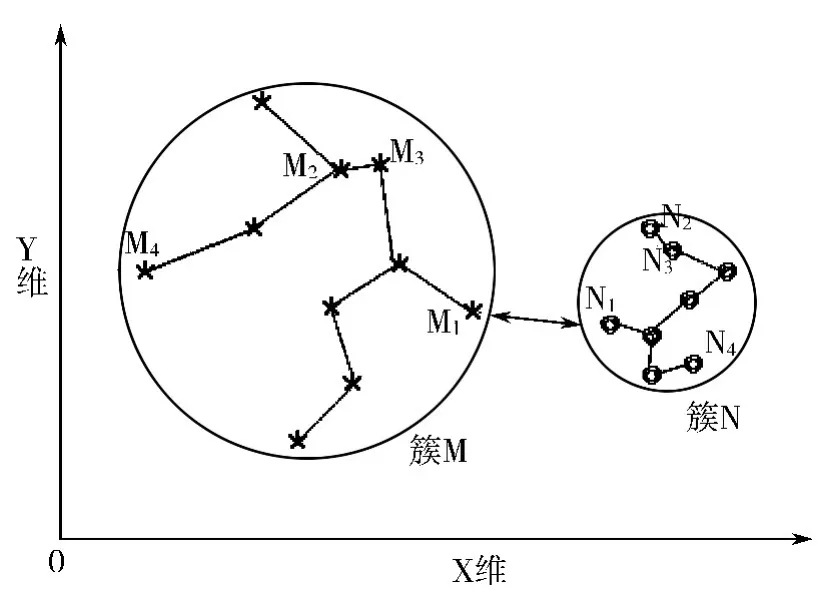
图2 DD-DBSCAN 算法相关概念示意图

以二维数据为例说明相关定义，如图2 所示。其中M、N 表示整个数据集中2 个不同的簇，其中分别包含m、n 个点。则:

任意一点Mi 表示为:

图2 中任意2 点Mi、Mj 间的距离为:

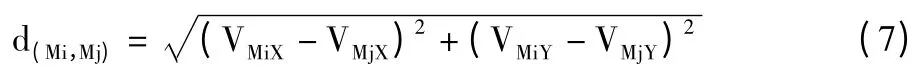
定义1 核心对象。点的Eps 邻域内的点的个数大于等于MinPts 这个阈值。

定义2 边界对象。点本身不是核心对象，但其Eps 邻域内包含至少一个核心对象。

定义3 直接密度可达。P 是核心点，Q 在P 的Eps 邻域内，那么Q 由点P 直接密度可达。

定义4 密度可达。在给定数据集中存在一个对象链P(1)、P(2)、...、P(n)，P(1)=Q，P(n)=P，如果P(i +1)由P(i)直接密度可达，则称P 从Q 密度可达，密度可达是非对称的。

定义5 簇。由任意一个核心点对象开始，从该对象密度可达的所有对象构成一个簇。

定义6 离群点。不能被划分到任意一个簇中的点(不是核心对象，也不由任一点直接密度可达的对象)。

定义7 点最小距离。点P 距离其在同一个集合中的各个点间距离的最小值，记为MinDp。

在图2 中，点M2 在簇M 中的最小距离为:

定义8 簇间距离。2 个簇S、T 中距离最近的点之间的距离，记为ClusterD(S，T)。

在图2 中，簇M 和N 的簇间距离为:

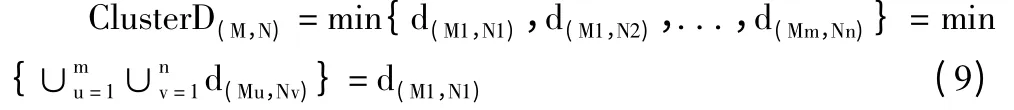
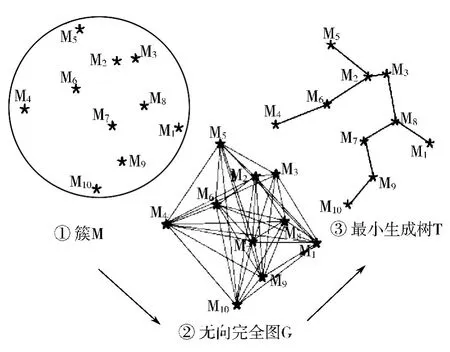
图3 DD-DBSCAN 算法中“定义9-簇密度”概念示意图

定义9 簇密度。簇S 中各个点MinD 的平均值，记为ClusterDensity(S)(如图3 所示，图中簇M 的簇密度即为以该簇各对象Mi 为顶点，以各对象之间的距离为边组成无向完全图G，然后以该图生成最小生成树T 的各边加权平均值)。

在图3 中，簇M 的簇密度为:

定义10 簇内最大(最小)距离。簇S 内各个点MinD 的最大值(最小值)，记为MaxDCS(MinDCS)。

在图3 中，簇M 内最大、最小距离分别为:

1.3 算法思路

如图4 所示，就像地图上的等高线一样，等高线之间距离大小即不同的疏密程度代表了地形地貌的陡缓程度。一般情况下，离群点就是指“远离”大部分数据的点，换句话就是指“邻居”数量较少的点，图4 中点a 至e 相对于簇X、Y、Z 内的点来说就是离群点。一个数据集经过聚类挖掘后，簇核心点(即核心对象)的邻域必然是数据分布相对密集的区域，而边界点(即边界对象)所在区域数据分布相对稀疏;在数据稠密的簇内，数据点距离其最近点的距离(即点MinD 值)的平均值(即簇ClusterDensity 值)较小，反之较大。由此易知，在图4 中，Y 区域所构成的簇与Z 区域所构成的簇相比，其ClusterDensity 值明显较大。

图4 DD-DBSCAN 算法思路示意图

在一个数据集中如果有N 个全局离群点，那么这些数据必然也是其MinD 值最大的点。图4 中，与点a 至e 最近点的距离明显要大于其它的点。在去除了全局离群点的一组数据中，如果在各个簇内，一个点在各个点平均最小距离和的μ 倍邻域内，点的个数达不到MinPts 这个阈值，那么这个点为离群点，这部分点主要集中在簇的边缘区域。

基于密度划分的离群点检测算法DD-DBSCAN就是根据以上思路设计，其实现步骤为:1)计算各个点之间的距离(如式(3)所示采用欧氏距离)，并且按照从小到大的顺序排列，然后依这个顺序将数据点分别合并到一个个簇中，直到剩余N 个未划分数据为止，并且把这些未划分的数据记为离群点;2)对第一步处理后簇密度和簇距离达到合并条件的簇进行合并，合并之后分别在各个簇中运用基于密度的聚类算法DBSCAN，分别检测出局部离群点。

以二维数据为例，核心对象和簇的数据结构设计如表1 所示。

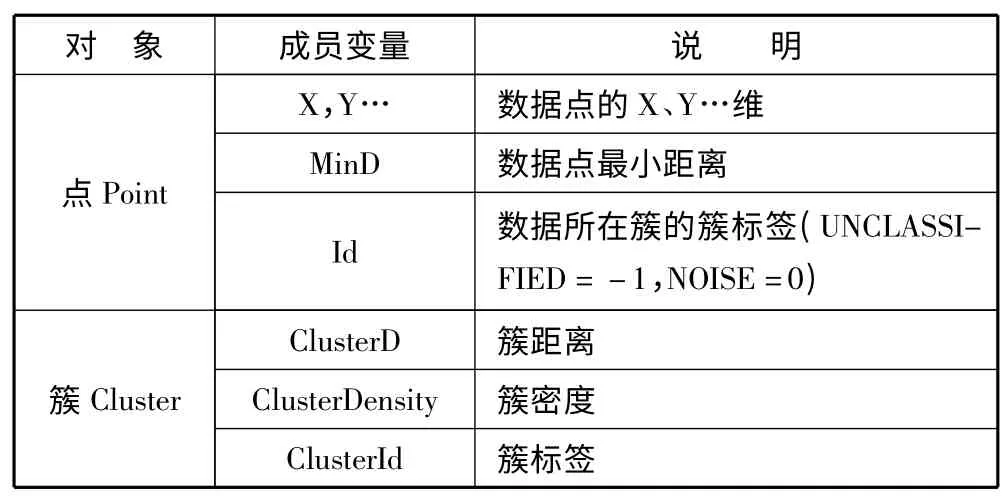
表1 核心对象和簇的数据结构

DD-DBSCAN 算法过程如下所示。

DD-DBSCAN 算法中基于密度聚类的离群点挖掘函数DBSCAN 运算过程，如下所示。

1.4 算法说明

1)数据次序对检测结果的影响:本文算法在数据读入后，首先要将数据按照点的MinD 值大小进行一次排序，在此基础上进行下一步实验。因此，检测结果不受数据读入次序影响，使得算法适应性增强。

2)全局离群点的检测:如1.3 节所述，全局离群点是其MinD 值相对比较大的点。因此，在第一步进行合并的时候，按照已经排好的次序，将没有被合并到任何一个簇的最后N 个点划为离群点，这几个离群点就是全局离群点。

3)初始簇合并的条件:经过第一步，数据集分离了全局离群点，并且将其余MinD 值大小相近的点分别连接成了一个个簇，这些簇需要进一步合并。合并的原则是，2 个簇的ClusterD 值小于2 个簇MaxDC 值中较小的一个，并且2 个簇的ClusterDensity 相比不超过2 倍。通过这一步将数据按照密度不同，划分成了若干个簇，使得DD-DBSCAN 算法能处理密度分布不均匀的数据。

4)参数Eps 的选择问题:本文算法的核心是基于密度聚类的检测算法，在第二步要分别对各个簇进行基于密度聚类算法的挖掘，需要输入参数Eps。由于在经过合并簇的步骤后，整个数据集已经按照密度不同而被划分成不同的簇，可分别求得各个簇的簇密度ClusterDensity，Eps 的值便以各个簇的ClusterDensity值为基数自适应设定。实验证明，当Eps 取值为μ倍的簇ClusterDensity 取值时，实验结果较为理想，(在本文第2 节实验中调整系数μ=1.25)。由于DD-DBSCAN 算法根据各个簇的簇密度，适时调整了密度聚类过程所需参数大小，无需反复输入任何参数试验，不需要先验知识做支撑，提高了算法的检测效率。

2 实验结果与分析

为验证本文算法的有效性，将通过实验来比较DD-DBSCAN 算法、DBSCAN 算法各自的覆盖率和准确率。实验的硬件环境是:CPU Inter Core Duo 1.66 GHz，主存2 G，微软Windows XP 操作系统，算法使用Java 语言编程实现。实验采用了一个2D 模拟数据集和一个真实数据集Iris Plants Database［14］。

2.1 数据准备

2.1.1 2D 模拟数据集

用一组二维数据模拟密度分布不均匀的数据集，共有80 条(通过人工控制分布区域和数量，以Java编程语言产生随机数的函数实现)，其中加入了20 条记录作为离群记录。数据基本分布情况如图5 所示。

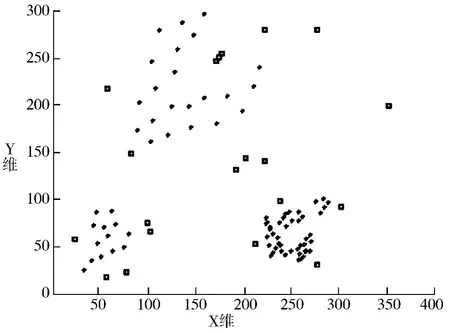
图5 2D Simulated Database 分布示意图(图中“□”标识的为离群点，“* ”为其余点)

2.1.2 Iris Plants Database

Iris Plants Database 来自UCI 网站，是美国加州大学信息与计算机科学系的Iris 数据集，夏鲁宁等人也用此数据做对比实验来验证聚类算法的效率［15］。它以鸢尾花的特征作为数据来源，来自美国UCI 标准数据集，该数据被广泛应用于聚类分析和分类分析实验中。数据集包含150 条记录，分为setosa、versicolor、virginica 3 个类，每类50 个数据，每个数据包含4 个独立的属性，它们分别是花萼和花瓣的长度和宽度，这些属性变量测量植物的花朵，比如萼片和花瓣的长度等。本实验在原始数据集的基础上，随机删除其中70 条，再加入20 条记录作为离群点，使得数据总计为100 条记录。

2.2 性能指标

根据给定数据集和实验结果，计算由此方法所挖掘出的离群点个数占数据集中离群点数的比例，比例越接近1，则表明此算法精度越高，性能越好;计算算法检测出的真正的离群点个数占所检测出的全部离群点数的比例，比例越高，则表明算法准确度越高，性能越好。2 个指标同时偏高的算法，为性能较好的算法。本实验采用以下2 个指标对算法进行评价，具体算法如下。其中，OA是算法检测到的离群点集合，OB是数据集中所有真实离群点数目的集合［16］。

2.2.1 覆盖率(Coverage)

覆盖率C 是指检测到真实离群点的数目与所有真实离群点数目的比值。

2.2.2 准确率(Precision)

准确率P 是指检测到真实离群点的数目与检测到的离群点数据数目的比值。

2.3 性能分析

文献［4］DBSCAN 算法描述中给出的参数选择方法是设定minPts=4，通过观察法来判断Eps。本节对于DD-DBSCAN 算法和DBSCAN 算法的对比实验中，对于基于密度聚类的部分，均设定minPts=4，分别通过自适应变化和人工变更参数Eps 来验证2个算法的差别。

2.3.1 2D 模拟数据上的实验结果

因为二维模拟数据集方便在图上显示，分别运用2 种算法挖掘后，其结果显示如图6～图10 所示，结果的具体数据如表2 所示。其中，图6～图9 所示的为运用DBSCAN 算法挖掘结果示意图，图10 为运用DD-DBSCAN 算法挖掘结果示意图，图中符号“□”表示检测出的离群点，其余符号“* ”为非离群点。

图6 在2D 模拟数据集上实验1(MinPts=4，Eps=10，离群点数=55)

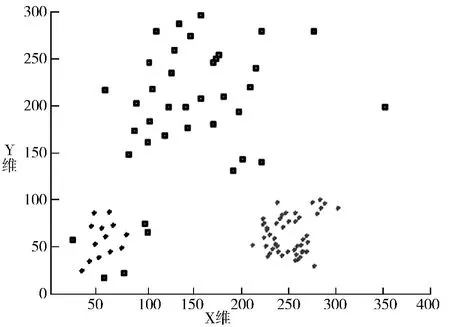
图7 在2D 模拟数据集上实验2(MinPts=4，Eps=20，离群点数=38)

图8 在2D 模拟数据集上实验3(MinPts=4，Eps=25，离群点数=20)

通过图6～图10 可以看到，运用DBSCAN 算法对数据进行挖掘时，在参数MinPts 固定的情况下，当Eps 取值越小时:由于能够符合核心点和与核心点密

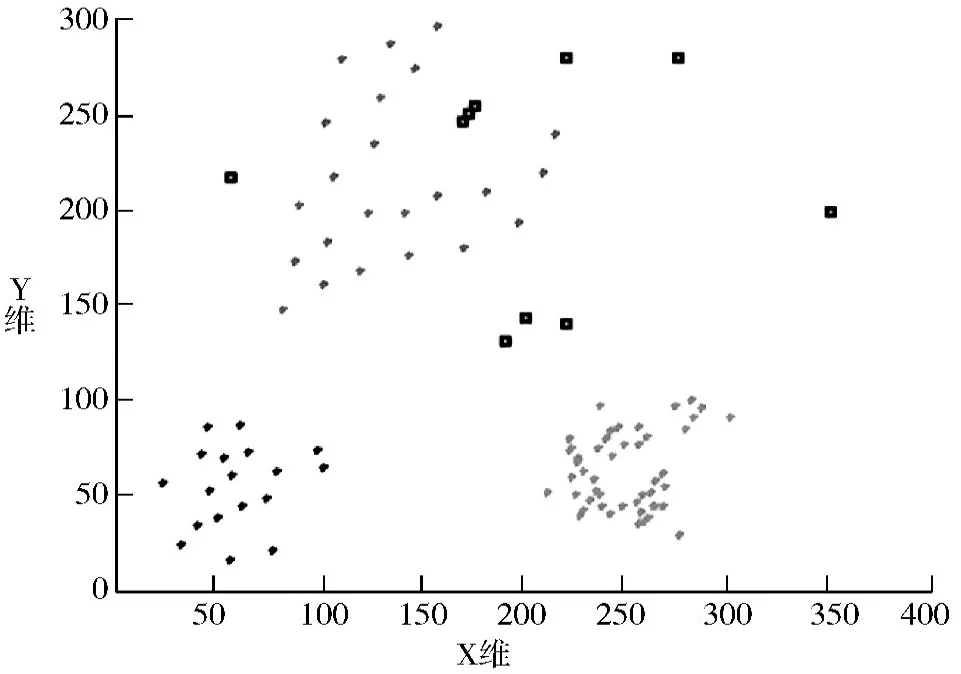
图9 在2D 模拟数据集上实验4(MinPts=4，Eps=30，离群点数=10)

图10 DD-DBSCAN 算法挖掘结果示意

度相连的点越来越少，使得检测出的离群点越来越多，如图6 所示，这些离群点中包括数据集中实际存在的全局离群点、一些远离簇核心点的局部离群点以及数据密度较稀疏的区域，也就是说该算法能够检测出离群点，但却存在过多的误判，即把本不是离群点的稀疏区域也判定为离群点。因此，根据第2.2 节定义，覆盖率C 较高，但是准确率P 较低。当Eps 取值越大时，DBSCAN 算法检测到的离群点越来越少，如图9 所示，此时只能检测到部分全局离群点，而无法准确检测到局部离群点，因此，覆盖率C 下降，而准确率P 上升。从实验看出，无论2 个参数怎么调节，DBSCAN 算法始终无法有效处理数据密度差异较大的数据。而如图10 所示，由于DD-DBSCAN 算法通过密度稀疏将数据集“分而治之”，能够在各个簇中分别自适应地调整参数，使得算法的检测结果较为理想，能够有效检测出局部和全局离群点。

2.3.2 Iris 数据集上的实验结果

在超过二维的数据集Iris 上的实验结果，如表2所示。

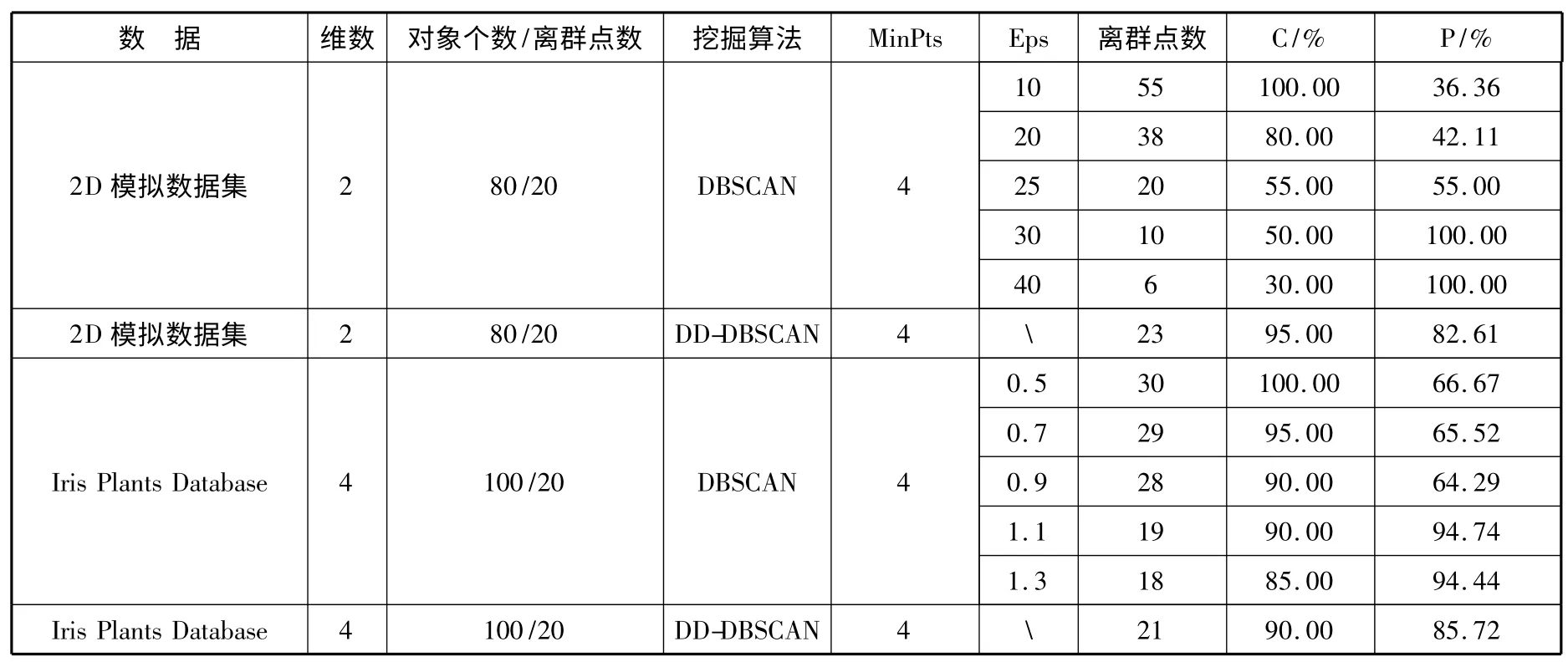
表2 DD-DBSCAN 算法与DBSCAN 算法在2 种数据上的挖掘结果对比

通过表2 可以看到，运用DBSCAN 算法进行检测时，当聚类半径Eps 值逐渐增大时，检测出的离群点数不断减少，算法不能有效地检测出所有的离群点，覆盖率C 呈下降趋势;当聚类半径Eps 值逐渐减小时，检测出的离群点数量不断增多，算法误判的数量也不断增多，导致准确率P 呈下降趋势。因此，DBSCAN 需要多次输入参数才能得到一个较为理想的结果，而且参数依赖人工输入，无法自动适应数据变化，使得算法的效率比较低，局限性较大。而本文提出的DD-DBSCAN 算法优点明显，能够在一次输入数据和参数后，得到理想的检测结果，无需反复输入参数进行试验，算法能够有效处理密度不均匀的数据集。在超过二维的数据上的实验结果表明，DD-DBSCAN 能够获得较高的覆盖率和准确率，具有较好的鲁棒性。

3 结束语

本文提出了一种基于密度划分的离群点检测算法DD-DBSCAN，并在2D 模拟数据集和Iris Plants 数据集上进行了检验。实验结果表明，本文算法相比DBSCAN 算法能够有效处理密度不均匀的数据，不需要用户设置参数MinPts 和Eps，通过自适应的方法自动确定参数，算法的精确度和正确率都比较高。下一步的研究方向为:基于DD-DBSCAN 算法，进行不确定数据流上的离群点检测算法研究，并且改进对象之间的相似性度量方法以适应高维混合属性数据特征，使得算法能够处理动态变化的大规模数据集。

［1］Hawkins D.Identification of Outliers［M］.London:Chapman and Hall，1980.

［2］Knorr M E，Ng R T，Tucakov V.Distance-based outliers:Algorithms and applications［J］.The VLDB Journal，2000，8(3-4):237-253.

［3］范洁.数据挖掘中孤立点检测算法的研究［D］.长沙:中南大学，2009.

［4］Ester M，Kriegel H，Sander J，et al.A density-based algorithm for discovering clusters in large spatial databases with noise［C］// Proceeding of the 2nd Internatioanal Conference on Knowledge Discovery and Data Mining.1996:226-231.

［5］王桂红.基于密度的聚类算法研究［J］.泉州师范学院学报(自然科学版)，2009，27(2):44-49.

［6］张卫旭，尉宇.基于密度的局部离群点检测算法［J］.计算机数字工程，2010，38(10):11-14.

［7］Ren Dongmei，Wang Baoying，Pcrrizo W.RDF:A density-based outlier detection method using vertical data representation［C］// Proceedings of the 4th IEEE International Conference on Data Mining.2004:503-506.

［8］傅德胜，周辰.基于密度的改进K 均值算法及实现［J］.计算机应用，2011，31(2):432-434.

［9］汪中，刘贵全，陈恩红.一种优化初始中心点的K-means算法［J］.模式识别与人工智能，2009，22(2):299-304.

［10］胡彩平，秦小麟.一种基于密度的局部离群点检测算法DLOF［J］.计算机研究与发展，2010，47(12):2110-2116.

［11］包小兵，翟素兰，程兰兰.基于信息熵加权的局部离群点检测算法［J］.计算机技术与发展，2012，22(9):59-65.

［12］Breuning M M，Kriegel H P，Ng R T，et al.LOF:Identifying sensity-based local outliers［C］// Proceedings of ACMSIGMOD International Conference on Management of Data，2000.2000:93-104.

［13］王晶，夏鲁宁，荆继武.一种基于密度最大值的聚类算法［J］.中国科学院研究生院学报，2009，26(4):539-548.

［14］MacQueen J B.Some methods for classification and analysis of multivariate observations［C］// Proceedings of the 5th Berkeley Symposium on Mathematics，Statistics and Probabilty.1967:281-297.

［15］夏鲁宁，荆继武.SA-DBSCAN:一种自适应基于密度聚类算法［J］.中国科学院研究生院学报，2009，26(4):530-538.

［16］唐向红，李国徽，杨观赐.快速挖掘数据流中离群点［J］.小型微型计算机系统，2011，32(1):9-16.