基于改进粒子群优化算法的无线传感器网络定位

2015-11-26李巧君

计算机与现代化 2015年7期

裴祥，李巧君

(河南工业职业技术学院计算机工程系，河南南阳 473000)

0 引言

无线传感器网络(Wireless Sensor Network，WSN)在实际应用中，只有确定节点的确切位置，才具有应用价值，因此提高传感器节点的定位精度具有重要的意义［1-2］。

当前定位方法分为距离和非测距的定位方法，基于距离的定位算法首先通过测量相邻节点间的距离来测量节点间距离或方位，然后采用最大似然估计法计算未知节点位置［2-3］。非测距的定位方法通过节点的连通信息获得未知节点的估计位置，如质心算法、APIT 算法、MDS-MAP 算法、DV-Hop 算法等［4-7］。DVHop 算法因为其成本低，易于实现，受到学者的广泛青睐［4-7］。依据DV-Hop 算法，研究者们已经进行了很多改进，如:利用平均跳数和平均误差来减小最终的定位误差，减小未知节点平均跳距的累积误差［8-11］，但是这些方法仍然有一些不足，如何设计更优的方法还是当前有待进一步研究的问题。

为了提高无线传感器节点的定位精度，针对DVHop 算法存在的问题，本文提出一种改进粒子群优化算法的节点定位算法(MPSO-DVHop)，并采用仿真实验对算法性能进行分析。

1 DV-Hop 算法及存在的问题

1.1 DV-Hop 算法

1)计算节点之间的最小跳数。锚节点向邻居节点广播信息数据包，包括它的位置坐标和跳数，如(xi，yi，hj)，(xi，yi)是锚节点i 的坐标，hj是锚节点距离其他节点的跳数，初始化为0。每个节点只接收来自其他锚节点的最小跳数。

2)计算锚节点的平均跳距。每个锚节点计算自己的平均跳距，计算方法如公式(1)所示。未知节点只接收距离它最近的锚节点的平均跳距。

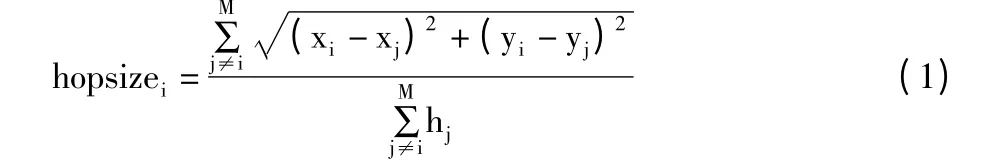
其中，hopsizei代表锚节点i 的平均跳距，M 代表锚节点数。(xi，yi)和(xj，yj)分别代表锚节点i 和j 的坐标。hj代表锚节点i 和j 之间的跳数。

3)利用极大似然估计法计算未知节点的位置信息，计算方法如式(2):

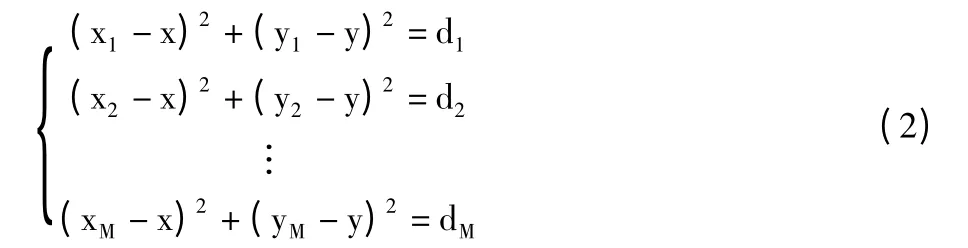
其中，(x，y)是未知节点的坐标，di是相应的锚节点i与未知节点之间的距离。

未知节点的坐标可以通过公式(3)得到:

其中:

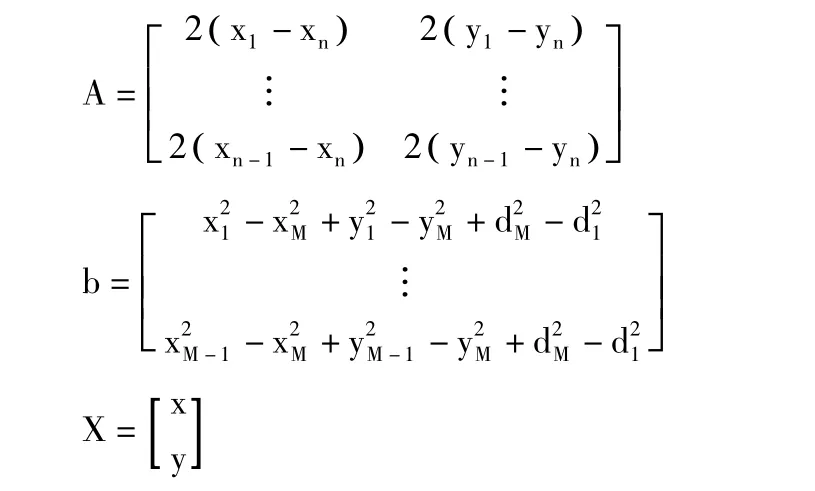
1.2 存在的问题

设锚节点(xi，yi)，i=1，2，…，n，与未知节点(x，y)的实际距离为ri，i=1，2，…，n，测距误差为εi，那么|ri-di| ＜εi，i=1，2，…，n。根据式(2)可知，(x，y)应该满足如下约束条件［15］:

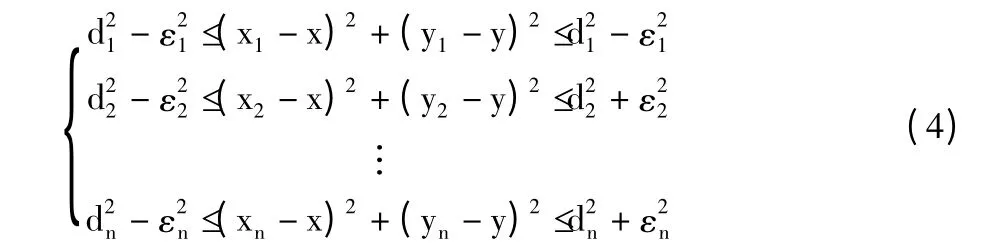
求解(x，y)，使得:

2 改进粒子群优化算法的无线传感器定位

2.1 改进的粒子群算法

PSO 算法通过以下2 个数学公式不断地更新训练集中粒子速度以及位置的取值:

其中，Vid和xid是第i 个粒子的速度及位置;Pid和Pgd是粒子i 及种群的历史最优位置;ω 是惯性权重;c1和c2是加速度学习因子。

在PSO 算法中粒子是通过Pid和Pgd进化的，在算法后期为了避免粒子陷入局部最优，并提高其他粒子在新区域搜索的能力，本算法在式(6)中增加一个高斯(0，1)分布的随机变量ε，在算法后期重新计算参数Pgd:

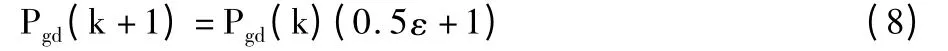
在式(8)中添加二次随机搜索因子η，即若粒子寻优到新位置不如当前位置，将在原位置开始下一次寻优，否则新位置是下一次寻优的起始位置［17］，具体如下:

其中，η=Rnd(0，1)+0.5。

2.2 MPSO-DVHop 算法步骤

图1 MPSO-DVHop 的节点定位流程

1)采用DV-Hop 算法的第一、二阶段定位技术，得到每个未知节点与各锚节点的跳数hi和网络跳距di。

2)初始化粒子群，粒子位置向量代表未知节点位置的一个可行解。

3)计算粒子适应度值，找到并记录Pid，Pgd。

4)更新粒子位置和速度。

5)与Pid和Pgd比较，更新个体最优值和全局最优值。

6)如果当前迭代次数小于最大迭代次数，则执行步骤5)。

7)全局最优粒子个体为未知节点的位置估计坐标。

基于MPSO-DVHop 的传感器节点定位流程图如图1 所示。

3 仿真实验

3.1 仿真参数

在Matlab 2012 仿真工具箱对MPSO-DVHop 算法的性能进行测试，选择与DV-Hop 算法、文献［17］改进DV-Hop 算法(MDV-Hop)进行对比仿真实验，仿真参数如表1 所示，为保证仿真结果的公平性，在每种测试条件下，对所有定位算法均进行10 次测试，取平均值作为最终结果，性能评价标准为归一化定位误差(error)，其计算公式为:

其中，(xi，yi)和)分别表示第i 个未知节点的实际坐标和估计坐标，R 为网络通信半径，N 为未知节点总数。

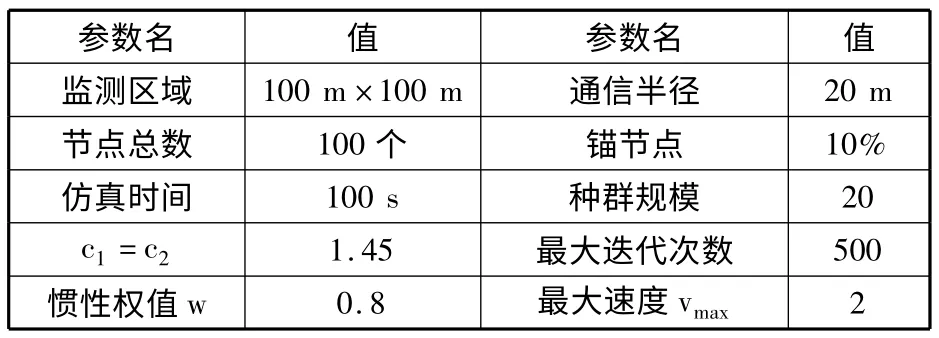
表1 仿真实验参数

3.2 结果与分析

3.2.1 定位误差比较

3 种算法的未知节点定位误差如图2 所示。从图2 可以看出，相对于DV-Hop、MDV-Hop 算法，MPSO-DVHop 算法的定位误差最小，MDV-Hop 算法次之，DV-Hop 算法的误差最大，而且MPSO-DVHop 算法的定位误差变化相当平稳，变化幅度相当小，实验结果表明，MPSO-DVHop 算法提高了传感器节点的定位精度，获得了更优的定位结果。

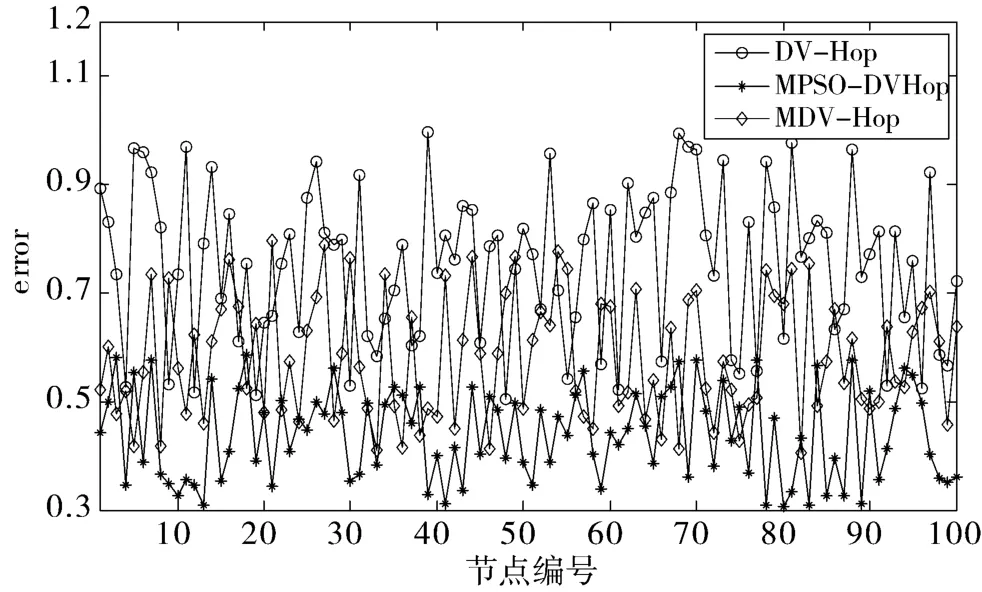
图2 不同算法的定位误差对比

3.2.2 不同锚节点数对定位性能的影响

由图3 可知，3 种算法定位误差与锚节点比例整体上成反比。在锚节点比例为5%～15%时，定位误差受锚节点比例影响较大;当锚节点比例超过15 后，3 种算法定位误差变化均趋于稳定。这是由于节点总数与通信半径一定时，锚节点越多，网络中可用来定位的节点信息越丰富，未知节点平均跳距信息越准确。MPSO-DVHop 定位误差在锚节点各种比例下均小于其它2 种算法，比DV-Hop 算法的平均定位误差减少了约20%，比MDV-Hop 算法平均减少了约10%。

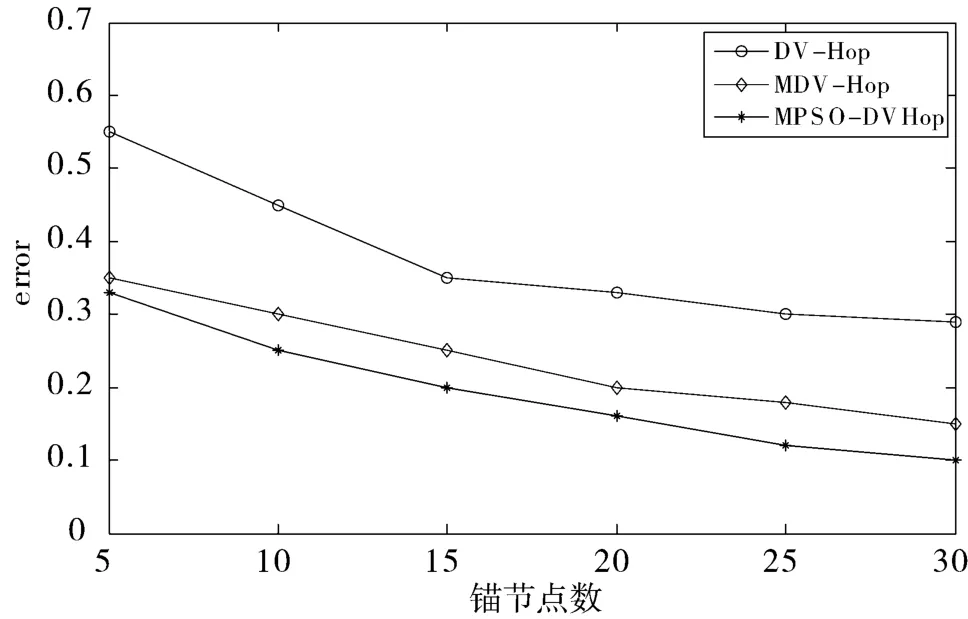
图3 锚节点比例对定位精度影响

3.2.3 通信半径的定位结果分析

由图4 可知，在节点总数及锚节点数一定的条件下，3 种算法定位误差与通信半径整体上成反比。这是由于通信半径越大，每个节点可通信的邻居节点越多，网络连通度越高，节点的平均跳距和跳数信息越准确。MPSO-DVHop 定位误差在各通信半径下均小于其它2 种算法，其平均误差相较于DV-Hop 算法、MDV-Hop 算法分别减少了约17%和8%。

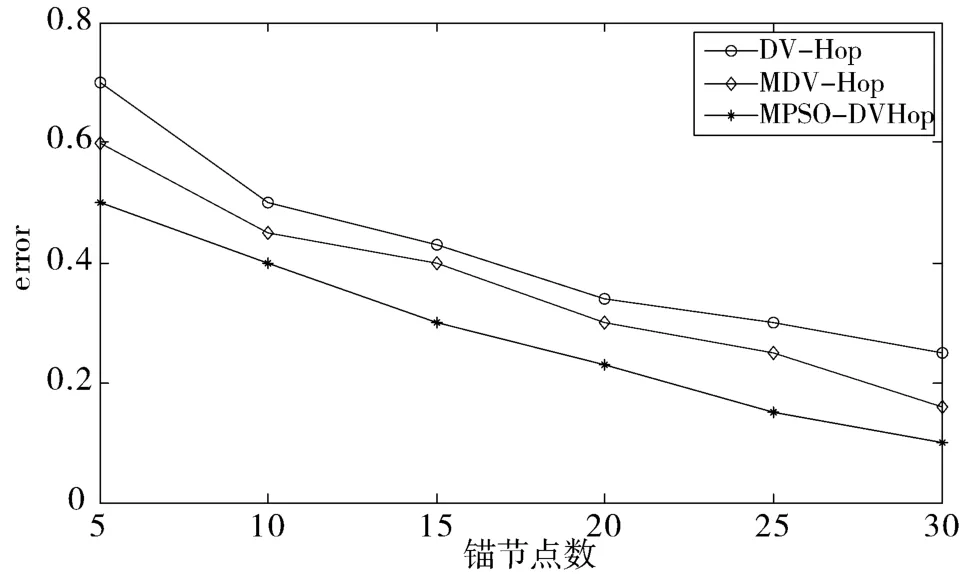
图4 通信半径对定位精度的影响

3.2.4 定位结果对比

3 种算法的节点定位结果如图5 所示。显然，MPSO-DVHop 算法的定位结果最优，误差最小，具有比较明显的优势。

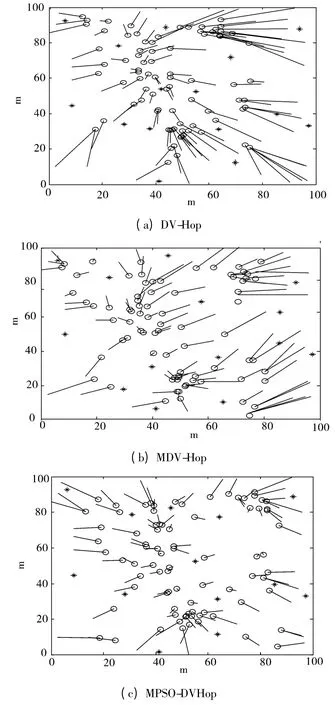
图5 3 种算法的定位结果对比

4 结束语

针对DV-Hop 算法存在的不足，采用改进粒子群优化算法对DV-Hop 算法未知节点位置进行优化，结果表明，本MPSO-DVHop 算法可以修正未知节点的估计坐标，具有较好的实际应用价值。

［1］Garg V，Jhamb M.A review of wireless sensor network on localization techniques［J］.International Journal of Engineering Trends and Technology，2013，4(4):1049-1053.

［2］刘瑾.基于测距的无线传感器网络的定位算法的研究［J］.航空计算技术，2009，39(6):124-126.

［3］鲍可进，王伟.一种单移动锚节点的无线传感器网络定位算法［J］.计算机应用研究，2010，27(4):1452-1454.

［4］毛永毅，李明远，张宝军.一种NLOS 环境下的TOA/AOA 定位算法［J］.电子与信息学报，2009，31(1):37-41.

［5］李兆斌，魏占祯，徐凤麟.无线传感器网络增强的质心定位算法及性能分析［J］.传感技术学报，2009，22(4):563-567.

［6］许屏，刘彬.撒布型无线传感器网络节点定位算法［J］.计算机工程与应用，2009，45(8):113-117.

［7］赵昭，陈小惠.无线传感器网络中基于RSSI 的改进定位算法［J］.传感技术学报，2009，22(3):391-395.

［8］周彦，文宝，李建勋.无线传感器网络节点近点加权质心定位方法［J］.计算机工程与应用，2012，48(1):87-89.

［9］张保峰，刘同佩，韩燕，等.基于TOA 的三维空间定位算法研究［J］.计算机工程与设计，2007，28(14):3364-3367.

［10］张佳，罗军勇，王艳，等.改进的无线传感器网络定位算法［J］.计算机工程，2009，35(6):133-136.

［11］张清国，黄竞伟，王敬华，等.一个新的无线传感器网络节点定位算法［J］.小型微型计算机系统，2009，30(3):460-464.

［12］邱岩，赵冲冲，戴桂兰，等.无线传感器网络节点定位技术研究［J］.计算机科学，2008，35(5):47-50.

［13］李辉，熊盛武，刘毅，等.无线传感器网络DV-Hop 定位算法的改进［J］.传感技术学报，2011，24(12):1782-1786.