信号控制下的动态路段行程时间模型

温凯歌

(长安大学电子与控制工程学院，陕西 西安 710064)

0 引言

在现代智慧交通中，动态交通分配(DTA，Dynamic Traffic Assignment)和动态路径诱导系统(DRGS，Dynamic Route Guidance System)是其中重要的组成部分，出行者在出行前和出行中都需要得到准确而快速的出行路线信息，因此，需要估计路网中各路段的行程时间。另外，交通管理者在进行路网运行管理时，也需要对路段行程时间进行实时动态预测。因此，准确的路段行程时间模型是智能交通系统研究和开发的一个重要方面。

传统的道路行程时间模型是美国的BPR(Bureau of Public Road)路阻函数，将路段的行程时间表示为路段交通流量的增量函数。然而，动态的行程时间才是最为迫切需求的，因此经典的BPR 模型在动态情况下不适用。国内方面，根据国内的机非混合的实际情况，对混合交通条件下的行程时间模型［1］也作了相应的研究。出行者对交通信息的实时性有较强的要求，因此动态条件下的行程时间的预测［2］和估计［3］以及行程时间的可靠性［4］成为研究的热点。

从交通管理者的角度来讲，如何均衡地利用道路网是需要重点关注的，因此在动态交通分配中，Daganzo［5］和Malachy［6］等人研究了行程时间函数在动态交通分配中的特性。在城市交通网中，路段的行程时间可以划分为车辆自由流运行时间和在交叉口信号灯处的排队延误时间。在这些研究中，车辆延误的计算是利用控制理论的模型，但是交通流作为一个整体而言，在交通控制中的延误考虑的并非单一辆车的实际延误，而是一个周期内路段车辆的平均延误，因此该方法具有较强的统计学意义，作为车辆延误的数学模型精度难以保证［7］。利用智能的方法来获取车辆延误也是一条途径，但是人工智能方法需要数据具有很高的实时性［8］，另外数据采集的精确性也会严重影响模型的精度。

本文通过对停车线前车辆排队的分析，划分了交通流在信号交叉口前的排队-消散模式，针对稳定的模式对车辆的行驶轨迹进行分类，并研究了其动态行程时间。

1 路段行程时间的划分

在有信号灯控制的城市交通网中，所谓路段均指含有一个相邻的下游交叉口的路段。当出行车辆进入特定路段后，在该条路段上的行程时间是受到当前交通流的影响。随交通流量的变化而行程时间也会发生变化，特别是车流量达到饱和及过饱和时，车辆间的影响明显，车速呈下降趋势。由于在下游交叉口信号灯的控制作用，有可能会产生停车等待，从而发生额外延误。因此在路段上的延误应包含行驶中和停车等待2 个部分，但是相对于等待，行驶中的延误几乎可以忽略不计［9-10］。因此，为了简化模型的建立，所以只考虑交通流量及红绿灯控制对车辆的影响。

根据车辆在拥挤路段行驶过程中所出现完全不同的行驶状态，可以将路段行程时间划分为3 个部分，即:车辆在路段上的自由行驶部分、在下游交叉口处的排队且走走停停的延误部分和通过交叉口所花费的时间。在t 时间段内路段上总的行程时间是3部分之和:

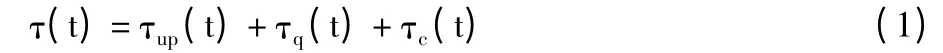
其中，τ(t)、τup(t)、τq(t)和τc(t)分别表示t 时刻车辆在路段上总的行驶时间、路段上游的自由行驶时间、下游交叉口处的排队等待时间以及通过下游交叉口的时间。

路段的总长度可划分成2 个部分:

为了建立模型，首先做出如下假设:

1)拥挤路段上的车辆排队长度不会超过路段总长度，也就是排队车辆不会到达上游交叉口;

2)在路段中行驶的车辆都遵守交通规则约束，即车辆在排队中行驶时不会发生超车现象，先进入队列的车辆先离开;

3)路段在t 时间段的路段驶入流率不会超过路段的通行能力，即u(t)≤Q;

4)在路段的上游自由行驶部分中，车辆处于自由行驶状态，与其他车辆的互相影响可忽略不计。

2 排队车辆数的计算

交叉口停车线前排队车辆数是模型的一个基本因素，在下面的大部分计算中都要用到它，所以在这里先给出排队车辆数的计算方法。

首先，计算出上游交通流密度，根据Greenshields的线性车速-密度关系，以及交通流基本关系有:

其中，u(t)是指在时间段t 内，路段上的动态驶入流率;Vup(t)为车辆在路段上游自由行使区的平均行驶速度;kup(t)为车辆在路段上游自由行使区的车流密度。则有:

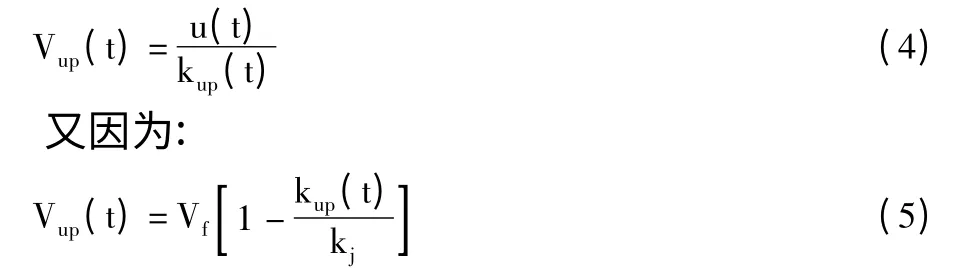
其中，Vf是指路段上的自由流行驶速度;kj为路段交通阻塞密度。

将式(5)代入式(4)可得:

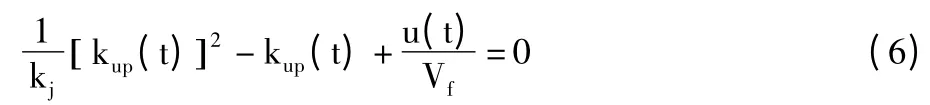
由于u(t)为路段的驶入流率，其它都是已知的量，因此式(6)是关于kup(t)的一元二次方程，该方程的解为:

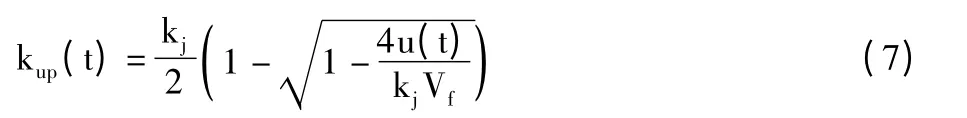
最后可以用式(8)计算出排队的车辆数:

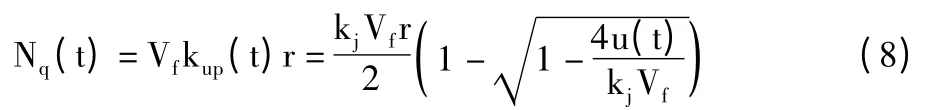
其中，r 是指交叉口红灯信号时间长度。

3 各部分行程时间计算

车辆在路段上总的行程时间等于各部分行程时间之和，各部分行程时间分别进行预测计算。

3.1 车辆在路段上的自由行驶部分

计算交叉口停车线前排队的长度，假设排队车辆的平均长度为S，通常取S=6 m，可以得到排队长度:

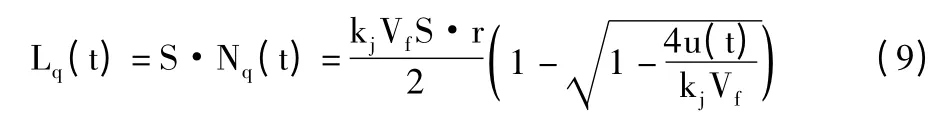
则车辆进入排队之前，在上游的行驶时间为:

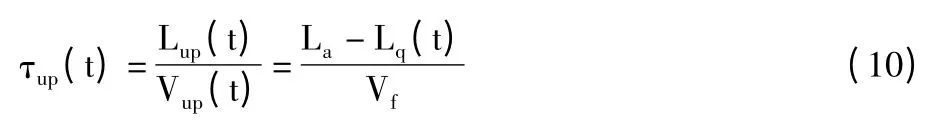
因为车辆在上游处于自由行驶状态，因此平均车速等于自由流行驶速度。

3.2 车辆在路段下游交叉口停车线前的排队延误行驶部分

车辆在信号交叉口的排队处于2 种状态之下，一种是等待状态(红灯)，另一种是通行状态(绿灯)。要描绘出每一辆车在交叉口处于何种状态将非常复杂，计算量非常巨大，而且在宏观的动态交通分配中也没有这个必要，因此，本文提出使用车辆在信号交叉口的平均排队延迟时间来计算总的路段行程时间。

在每一个红灯期开始时，排队开始形成，而在红灯结束绿灯期开始时，排队开始消散。所以车辆在交叉口的排队延误可以简化为红灯等待时间和绿灯消散时间。在一个红灯期内车辆在交叉口的排队数为Nq(t)，绿灯开放以后车辆假设以饱和流率qs驶出交叉口，直到排队消散为止。而排队消散所需要的时间是排在队列末尾的车辆的延误时间，可以由式(11)计算出来。

车辆在信号交叉口的延迟时间包括红灯等待时间和驶离时间(排队消散时间)。所以每一辆车的平均排队延误时间，也要分成2 个部分进行计算。

1)假设排队最末尾的一辆车进入队列时，红灯结束，绿灯开始，则该车辆需要等待红灯的时间为0，排队中第1 辆车的红灯等待时间为r。因此，将等待时间从0 到r 用排队车辆数进行等分。末尾第1 辆车的红灯等待时间为0，倒数第2 辆车为，倒数第3 辆为，以此类推，倒数第i 辆为，队列第1 辆车为=r。然后对所有车辆的等待时间求和，再除以排队车辆数，最后得到每一个车辆的平均红灯等待时间τwr(t):

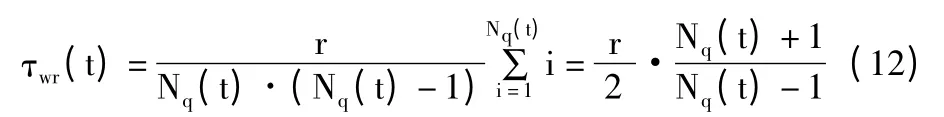
2)计算车辆队列消散时平均每一辆车所用时间。

假设排在第一位的车辆所用时间为0，排在末尾车辆所用时间为τd(t)。具体算法与上面相同，可得每一辆车的平均消散时间τwd(t):

最后，每一辆车总的平均排队延迟时间等于平均红灯等待时间和平均排队消散时间之和:

将式(11)、式(12)、式(14)代入(15)式整理得:

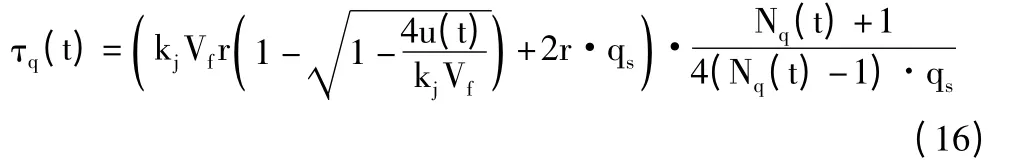
3.3 车辆通过下游交叉口所用的时间

路段通行能力和绿信比相乘，然后求其倒数便得到单个车辆通过交叉口所需的时间。

其中，Q 表示路段的通行能力;C 和g 分别为交叉口信号周期和绿灯信号时间长度。

3.4 总的路段行程时间

在时间段t 内通过路段的总行程时间等于以上3部分之和:

4 仿真算例

为了验证实验结果，采用Matlab 设计整个仿真过程。选用长度为400 m 的路段作为仿真对象，其包含一个下游信号交叉口。其它交通流参数设置为:路段交通阻塞密度kj=180 veh/km/Lane，车辆自由流速度Vf=60 km/h，路段最大通行能力设置为1800 veh/h。

为了验证不同的情况下模型的适应度，对于交叉口的信号灯设置参数，令信号控制周期长度为80 s和120 s，信号绿信比为0.4，路段入口流量分别为u=500 veh/h 和u=900 veh/h，因此可以分4 种组合来计算车辆行程时间，仿真结果如图1 所示。仿真时间从一个绿灯结束而红灯信号开始时进行，所有排队的车辆都可以在一个灯时通过交叉口。

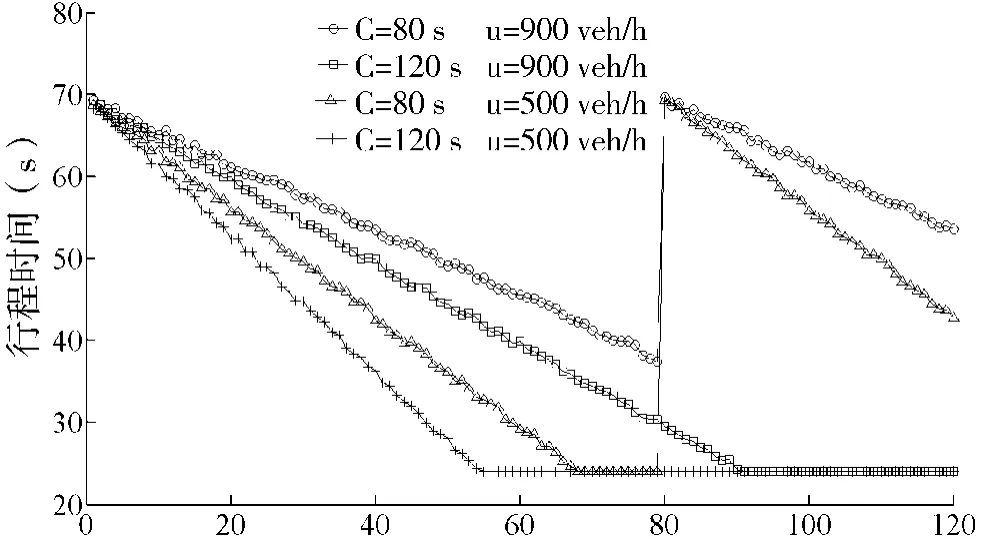
图1 进入路段时间(s)

由图1 中可以看出，由于信号灯的控制作用，动态行程时间表现出的是一个间断函数。该函数除了与路段的交通流量有很强的相关性之外，还与车辆进入路段的时刻也有较强的相关性。因此，在信号灯的控制作用下，车辆的动态行程时间不能表达成简单的流量递增函数，而是由交通流量、控制参数以及道路特征等因素共同决定的。

5 结束语

本文提出了一种新的动态路段行程时间模型，该模型是实际情况的一种近似表达，计算简单，有利于在动态交通分配中进行实际应用。该模型只需要采集路段入口处的驶入流率以及路段的交通阻塞密度，而其它的数据如:红灯时间、路段通行能力等都是常量很容易获得。所以该模型实现起来非常简单，比较适合于大型交通网络实时动态交通分配和动态路径诱导。相比于以往的模型，本文提出的行程时间模型有如下优点:

1)运算量小，运算速度快，可以同时处理大型路网的许多信息;

2)所需的信息易于采集;

3)兼容性较强，可以依据实时交通信息进行行程时间预测。

但是由于该模型求出的是平均行程时间，所以不利于微观网络上单个车辆的实时交通信息预测，只适合于宏观网络。

［1］四兵锋，钟鸣，高自友.城市混合交通条件下路段阻抗函数的研究［J］.交通运输系统工程与信息技术，2008，8(1):68-73.

［2］李进燕，朱征宇，刘琳.基于简化路网模型的卡尔曼滤波多步行程时间预测方法［J］.系统工程理论与实践，2013，3(5):1289-1297.

［3］于德新，高学英，杨兆升.基于GPS 数据及车辆运行特性分析的单车路段行程时间估计［J］.吉林大学学报(工学版)，2010，40(4):965-970.

［4］Arezoumandi Mahdi.Estimation of travel time reliability for freeways using mean and standard deviation of travel time［J］.J.Transpn.Sys.Eng ＆ IT，2011，11(6):74-84.

［5］Daganzo C F.Properties of link travel time functions under dynamic loads［J］.Transportation Research Part B:Methodological，1995，29(2):95-98.

［6］Malachy Carey，McCartney M.Behavior of a whole link travel time model used in dynamic traffic assignment［J］.Transportation Research Part B:Methodological，2002，36(1):83-95.

［7］王殿海，祁宏生，李志慧.信号控制下的路段行程时间［J］.吉林大学学报(工学版)，2010，5，40(3):654-660.

［8］Jan Fabian Ehmke，Stephan Meisel，Dirk Christian Mattfeld.Floating car based travel times for city logistics［J］.Transportation Research Part C:Emerging Technologies，2012，21(1):338-352.

［9］杨兆升.智能运输系统概论［M］.北京:人民交通出版社，2003.

［10］史忠科，曲仕茹.交通控制系统导论［M］.北京:科学出版社，2003.