基于小波变换的含噪图像边缘检测算法

郝红转，张维强

(深圳大学数学与计算科学学院，广东 深圳 518060)

0 引言

图像边缘是图像最基本的特征，包含着有价值的目标边界信息，是图像的像素值发生突变的地方，边缘检测对图像识别、特征提取、图像分割和图像增强等有着重要的意义。在工程应用中，对目标特征提取和特征分析要求既能对目标精确定位又能够很好地抗噪，因此很多研究者热衷于对边缘检测算法的研究，以此来满足工程中的需求［1］。

文献［2］中详细介绍了传统的边缘检测算子有:Roberts 算子、Sobel 算子、Prewitt 算子、Laplace 算子和Canny 算子等，但传统的边缘检测算子对图像边缘的检测效果并不理想，处理图像时一般采用的步骤是平滑去噪和边缘检测，在平滑去噪时增加了边缘定位的不确定性，在边缘检测时又因提高了检测算子对边缘的敏感性，其抗噪性减弱，因此传统的边缘检测算子对抑制噪声和边缘的精确定位无法同时满足。

小波变换［3-5］具有多尺度分析的特点，通过选取合适的滤波器，能够减小或去除所提取的不同特征之间的相关性，从而有效地从图像中提取目标信息，可以较好地抑制噪声，但是在抑制噪声的同时也丢失了部分的细节信息，使边缘出现不连续的现象。因此本文采用小波变换提取图像边缘Edge，然后对得到的边缘图像作双阈值处理，其中文献［6-8］等对双阈值中高阈值的选取一般都只是采用人为设定的方法，而本文根据图像大小和像素点像素给出具体公式来确定高阈值，从而阈值处理得到2 个图像G1 和G2，再在G1 的基础上，以G2 作为补充图像来连接图像的边缘，进而得到滤除噪声后又能精确定位的边缘图像。

1 改进的小波变换梯度算法

小波变换的多尺度特性使得图像的边缘信息在每个尺度中都存在，尺度越低，边缘信息越多，但对噪声越敏感;尺度越大，边缘信息越稳定，抗噪性越好，但定位精确度不高。为保证阈值处理前的边缘图像含有较多的边缘信息，只对原始图像进行一次二维小波变换。

二维平滑函数θ(x，y)，令:

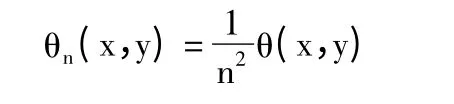
二维信号f(x，y)的平滑是通过在不同尺度n 上与θn(x，y)作卷积来实现［9-12］，表示为:

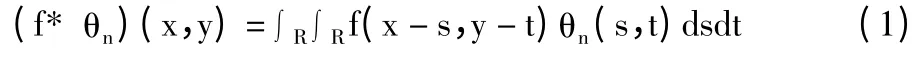
定义二维小波函数ψ1(x，y)和ψ2(x，y):

设f(x，y)∈L2(R2)，则一次二维小波变换包含2个方向的分量:

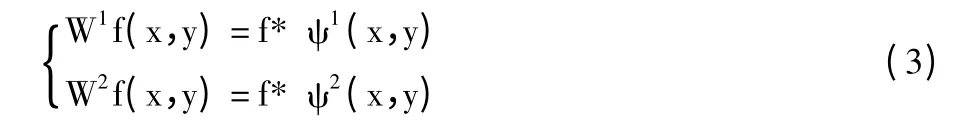
容易证得:

二维信号f(x，y)经过一次二维小波变换的梯度模值为Mf(x，y):

本文定义:

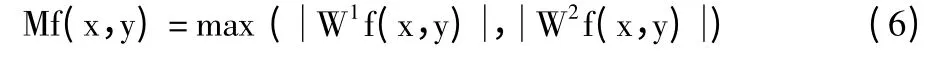
在工程应用中，为了快速简单计算，可取同位置梯度分量的最大值作为该点的模值即上式(6)，因为本文所采用局部模极大值边缘检测和阈值结合算法属于双层去噪和去伪，为防止过多的细节信息丢失，可适当地选取较小的模值，又根据向量的2-范数大于等于∞-范数的性质，此处用∞-范数代替2-范数。

记小波变换相角为Af(x，y):

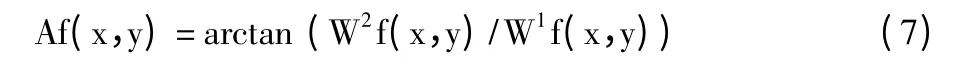
若像素点(x，y)的模值Mf(x，y)大于等于沿梯度方向Af(x，y)两个相邻像素点的模值，则判定该点为可能的边缘点。此时梯度方向可取8 个方向［13］，实际计算中可用4 个方向:0°(180°)方向、90°(270°)方向、45°(225°)方向、135°(315°)方向。

2 改进的阈值方法检测和连接边缘

本文采用的阈值方法是首先对小波变换得到的模局部极大值边缘图像Edge 进行阈值T 处理得到图像G1，其中Edge 经过归一化，Edge 中像素点值属于［0，1］。

令:

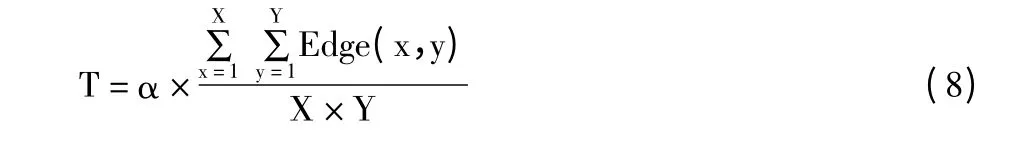
其中，α 选取0.0001 ±β(0 ≤β ＜0.00005)，使得T∈(0，1)，X×Y 表示图像的大小。

对于α 的取值，以分别添加椒盐噪声和高斯白噪声的Rice 图像为例，比较本文算法中α 取0.000 2、0.000 15、0.000 1、0.000 05 时的图像效果，实验图如图1 和图2 所示。

图1 加椒盐噪声时，α 不同取值对结果的影响

图2 加高斯白噪声时，α 不同取值对结果的影响

根据图1 和图2 可见，α 取大于0.000 1 的0.000 2和0.000 15 时，高阈值取值过大，噪声虽完全去除，但同时保留的图像边缘信息不完整，提取出的图像边缘不连续;α 取小于0.000 1 的0.000 05 时，高阈值过小，使得噪声不能完全去除而产生部分伪边缘;至于α 取小于0.000 05 时，噪声影响更大，此处不予说明。综上，无论是添加椒盐噪声还是添加高斯白噪声，本算法α 取0.000 1 ±β 时效果最优，其中β∈［0，0.000 5)。

取:

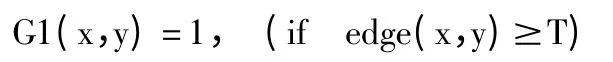
同时对边缘图像Edge 取阈值T'，其中T' ＜T，根据反复实验，取时效果较好，取:

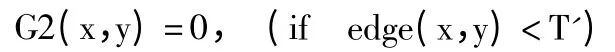
一般来说，图像Edge 中如果像素点(x，y)的灰度值Edge(x，y)∈［0，1］，因为阈值T'较低，所以保留较多细节信息，但是噪声也较多;因为阈值T 较高，所以噪声较少，但也损失了部分边缘信息;如果像素点的梯度值T'≤Edge ≤T，则此像素点可记为准像素点，因此以G1 为基础，以G2 为补充，来连接图像的边缘。

连接边缘图像［14］时，先扫描G1，假定灰度像素点E 为一个非零值，则跟踪以点E 为开始点的轮廓线直到该轮廓线的终点F，在G2 中，考察与G1 中E点位置对应的点E'的24 个邻域，如果在点E'的24个邻域中有非零像素F'存在，则将其包括到G1 中，作为点H，从H 开始继续寻找G2 中相对位置邻域的非零像素点，由此下去直到无法继续为止。当包含点E 的轮廓线的连接结束时，将其标记，回到开始，寻找下一条轮廓线，重复进行直到G1 中再也找不到新的轮廓线为止。

3 算法步骤

通过以上的分析，给出结合小波变换和阈值方法的具体步骤:

1)添加椒盐噪声(也可以添加其它类型噪声)到原始图像，得到加噪图像f(x，y);

2)对加噪图像f(x，y)进行一次二维小波变换，根据式(6)和式(7)生成Mf(x，y)和Af(x，y);

3)通过检测沿相角4 个方向的小波变换模的局部极大值点得到可能的边缘图像Edge;

4)对边缘图像Edge 取阈值T 和T'，得到2 个边缘图像G1(T)和G2(T');

5)以G1 为基础，以G2 为补充来连接图像边缘。

算法流程见图3。

图3 算法流程图

4 实验结果及分析

分别以256 ×256 的Rice、Cameraman 图像添加方差为0.05 的椒盐噪声和方差为0.2 的高斯白噪声为例进行实验，对本文所提出的算法进行验证，取α=0.0001，，其他传统算法都是先均值滤波预处理，之后利用算子处理得到的图像边缘，这里选取3 ×3 和4 ×4 的窗口模板，以便比较。边缘检测结果如图4～图7 所示。

4.1 对原图像加方差为0.05 的椒盐噪声

图4 Rice 图像(加0.05 椒盐噪声)

图5 4 ×4 均值滤波的Rice 图像

图6 Cameraman 图像(加0.05 椒盐噪声)

图7 4 ×4 均值滤波的Cameraman 图像

图4～图7 都是对Rice、Cameraman 原图像加方差为0.05 的椒盐噪声，根据图4 和图6 可知，对于Rice 图像来说，传统算法中首先利用3 ×3 窗口均值滤波处理的Canny 算法较好，但Canny 算法处理Cameraman 含噪图像时效果却较差，见表2。文献［14］算法结果线条较粗，不能清晰地提取出图像边缘，表1 及表2 中亦显示其MSE 较大，PSNR 较小。

均值滤波器是对椒盐噪声处理效果比较突出的一种常见滤波方法，因此，此处另选择4 ×4 窗口滤波以作比较，根据图5 和图7 可知，滤波窗口越大，信息越少，边缘连续性越弱，另5 ×5 窗口滤波效果更不如4 ×4 窗口滤波，不再作图说明。

表1 和表2 分别是对加椒盐噪声的Rice 图像和Cameraman 图像定量分析去噪效果，以传统Canny 算子提取原图像边缘为标准。

表1 加椒盐噪声的Rice 图像去噪效果比较

表2 加椒盐噪声的Cameraman 图像去噪效果比较

4.2 对原图像加方差为0.2 的高斯白噪声

图8 Rice 图像(加0.2 高斯白噪声)

表3 加高斯白噪声的Rice 图像去噪效果比较

表4 加高斯白噪声的Cameraman 图像去噪效果比较

图9 Cameraman 图像(加0.2 高斯白噪声)

图8 和图9 是分别对Rice 图像和Cameraman 图像添加方差为0.2 的高斯白噪声，传统算法中依然是先利用3 ×3 窗口均值滤波去噪再处理图像，根据图像可知，对于含高斯白噪声的图像，传统算法的去噪效果不稳定，如图8(g)3 ×3 窗口均值滤波后利用Canny 算子处理效果良好，得到的图像边缘亦为单像素宽，表3 中亦显示MSE 较小，PSNR 较大。但图9(g)中对于Cameraman 图像，去噪效果较弱，图9(e)算法对于去除高斯白噪声效果良好，图像边缘较连续，但对于同样算法的图8(e)，提取的边缘信息却较少，使得图像边缘不连续，因此传统算法的通用性一般。文献［14］中结合Canny 算子和形态学提出的算法能够很好地去除噪声的影响，边缘较连续，但因为双阈值的人为设定导致边缘信息不足，不能得到完整的边缘图像。本文算法去噪效果良好，边缘定位亦为单像素宽，能够较好地提取出图像边缘信息，优于传统的检测算法。

5 结束语

本文针对含噪图像边缘检测中噪声去除和边缘细节保留的问题，提出了一种基于小波变换的含噪图像边缘检测算法，采用小波变换能够分离连续的边缘信息和不连续的噪声信息的性质，对图像进行小波变换，从而求出图像边缘，然后利用新的阈值方法对边缘图像作用，最后连接图像。实验结果表明本算法能很好地抑制噪声，而且较好地保留了边缘细节，去除了伪边缘，检测效果良好。

［1］Canny J.A computational approach to edge detection［J］.IEEE Trans.Pattern and Machine Intelligence，1986，8(6):679-698.

［2］伍尤富.图像处理中边缘检测研究方法［J］.舰船电子工程，2006，26(4):35-38.

［3］章国宝，叶桦，陈维南.基于正交小波变换的多尺度边缘提取［J］.中国图形图象学报，1998，3(8):651-654.

［4］权建峰，李艳，郭东敏，等.小波变换模极大值方法对信号的奇异性检测［J］.探测与控制学报，2009，31(2):46-49.

［5］解梅，马争，顾德仁.一种改进的基于小波变换图像边缘检测算法［J］.系统工程与电子技术，1998，20(10):67-70.

［6］黄剑玲，郑雪梅.一种改进的基于Canny 算子的图像边缘提取算法［J］.计算机工程与应用，2008，44(25):170-172.

［7］李安安，何坤，詹晓倩，等.多尺度下的噪声图像边缘检测［J］.计算机工程与设计，2011，32(1):228-231.

［8］徐亮，吴海涛，孔银昌.自适应阈值Canny 边缘检测算法研究［J］.软件导刊，2013，12(8):62-64.

［9］阿卜杜如苏力·奥斯曼，吐尔洪江·阿布都克力木，马丽亚木·阿布来孜.综合颜色特征与形状特征的图像检索算法［J］.计算机工程与应用，2014，50(2):183-188.

［10］连静，王珂.样条小波自适应阈值多尺度边缘检测算法研究［J］.系统仿真学报，2006，8(6):1473-1482.

［11］王培珍，孟祥昊，张克，等.板材图像边缘检测算法研究［C］// The 25th CCDC.2013:5123-5127.

［12］Jiang Lixia，Zhou Wenjun，Wang Yu.Study on improved algorithm for image edge detection［C］// IEEE the 2nd International Conference on Computer and Automation Engineering (ICCAE).2010，4:476-479.

［13］王恩国，高印寒，苏成志.梯度方向图像分解的直线边缘提取算法［J］.红外与激光工程，2012，41(12):3423-3428.

［14］鲁金云，潘海鹏，夏永明.结合CANNY 算子和数学形态学的焊缝图像边缘检测算法［C］// Proceedings of the 32nd Chinese Control Conference.2013:4467-4470.