极限与极端思维在高中物理中的应用

梅鑫华

摘 要：不少物理教师将极限与极端混为一谈。本文试图对此做出区分，并探寻高中物理教材中的极端与极限思维，举例说明两种思维在解题中的应用。

关键词：极限思维；极端思维；物理应用

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）10-0049-3

人教版物理必修1在引出瞬时速度概念的过程中，采用了极限的思维。若把这种思维称作极端思维，显然有失偏颇。而在高中物理教学中，不少教师将极端与极限思维混为一谈，甚至有些文献也认为“极端思维又叫做极限思维”[1]。严格说来，极限与极端是两种有区别的思维方法。若教学中将两者混淆，必然不利于学生形成正确的极限概念。笔者认为有必要对此做一区分，便于学生理解与掌握两种思维的精髓。

1 极限思维与极端思维的区别

在数学中，如果某个变化的量无限地逼近于一个确定的数值，那么该定值就叫作变化的量的极限。这里隐含了极限思维的内涵：无限趋近或逼近。例如，函数y=，其中x≥1。利用极限思维，使x无限趋近+∞，可得y无限逼近0，所以0是函数y在x→∞时的极限值。而极端思维类似于数学中的特殊值法，是一种“极端”的特殊。例如，上述函数在取x=1这种“极端”特殊情况下，y的值将变为1。

中学阶段的极限与极端思维用数学语言可归纳如下：极限思维是指“使自变量趋近某一值，研究因变量无限逼近的极限值”；极端思维是指“取自变量为某些极端值，研究因变量的数值”。由于有些自变量无法直接取为极端值，如上述函数x不能直接取为0，所以需要极限思维，使x无限趋近于0，来研究因变量y的极限值。

对中学物理而言，两种思维的区别：极端思维是将所研究的问题直接推到极端状态下进行分析、讨论；而极限思维则是将所研究的问题无限趋近于极端状态来进行分析、讨论。

2 极限思维在高中物理中的体现

2.1 引出瞬时物理量的概念、方向

极限思维引出瞬时物理量的概念、方向在高中物理中有很多例子，如瞬时速度、曲线运动速度方向、向心加速度方向，这里不再过多描述。

2.2 推导物理公式、规律

由于极限思维是微积分的基础。高中物理教材在利用微积分思想推导公式、规律时，也渗透了极限的思维。

例如，匀变速直线运动位移公式的推导。首先利用微积分思想，将物体的运动分成几个小段，各小段的位移在v-t图像上近似表示为矩形面积。将这些矩形面积累加求和，即为全过程的位移。利用极限思维，使全过程无限分割，即相邻时间间隔趋近于零，此时累加求和的值将无限逼近图像上梯形的面积，由此得到匀变速直线运动的位移公式。此外，弹簧弹性势能公式、重力做功、静电力做功的推导与之类似。

3 极端思维在高中物理中的体现

极端思维类似于特殊值法，其主要用于解决物理问题，而在推导物理公式与规律中应用较少。因此，高中物理教材中极端思维的应用并不多，如表1。

4 极限思维与极端思维在物理解题中的应用

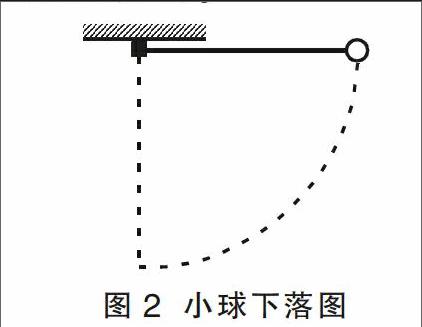
例1 （极限思维应用）空间某一静电场的电势φ在x轴上分布如图1所示，x轴上两点B、C的电场强度在x方向上的分量分别是EBx、Ecx，下列说法中正确的有（ ）

A.B、C两点的电场强度大小EBx

B.EBx的方向沿x轴正方向

C.电荷在O点受到的电场力在x方向上的分量最大

D.负电荷沿x轴从B移到C的过程中，电场力先做正功，后做负功

分析 由于B点斜率绝对值大于C点，所以EBx大于Ecx，即A选项错。沿电场线方向，电势降低，所以B选项错。O点处的斜率为零，所以电场强度为零，电场力最小，即C选项错。根据W=Uq，可知D选项正确。

点评 此题φ-x图像的斜率表示电场强度，这里隐含了极限的思维。以B点为例，在距B点右侧（或左侧）附近Δx处取A点，则A、B两点的电势差Δφ与Δx的比值可近似表示B处电场强度。使A点无限趋近于B点，即Δx趋向于零，此时E=将无限逼近该处切线斜率的大小，该斜率即为B处电场强度大小。

例2 （极端思维应用）如图2，一根不可伸长的轻绳系一个小球，将小球拉至水平位置后由静止释放，则小球在摆动到最低点的过程中，重力对小球做功的瞬时功率（ ）

A.始终不变

B.始终增大

C.先减小后增大

D.先增大后减小

分析 在小球下落过程中，由于速度沿重力方向的分量逐渐减小，而速度逐渐增大，导致难以判断下落过程中重力瞬时功率的大小变化。对此，我们进行定量分析。

设小球下落至某一点处，此时绳与水平方向的夹角为θ，设绳长度为R，那么该处小球重力的瞬时功率为：

P=mgvcosθ。

根据动能定律mgRsinθ=mv2，

联立两式得：

P=mgcosθ=mg。

由数学计算可知，从最高点到最低点，重力瞬时功率P先增大后减小，且sinθ=时，功率P达到最大值，答案选D选项。此题不妨应用极端思维，考虑到最高点及最低点时的功率都为零，而中间过程功率不为零，由此推出功率必然先增大后减小。

点评 极端思维用于判断物理量的变化情况时，可以帮助我们快速解决问题，节省做题时间，应用较为广泛。但对于何处达到最大或最小、具体数值为多大等问题，还需进行严密的物理分析与数学计算。

5 小 结

应用极限思维，可以引出一些瞬时物理量的概念，如瞬时速度、瞬时功率等；可以得到瞬时矢量的方向，如曲线运动速度方向沿切线方向、向心加速度方向；还可得到物理量在某处的大小，如电场强度大小。此外，极限思维配合微积分思想，能求解一些变力做功等问题。

应用极端思维，可以使我们快速、巧妙地解决物理问题，检验解题结果的正确性，对某些选择题尤为适用。这种思维具有跳跃性、灵活性等特点。

参考文献：

[1]方小宁.重视极端思维在物理中的应用[J].物理教学探讨，2004，22（8）：23—25.

（栏目编辑 陈 洁）