例谈高中物理竞赛中Maclaurin公式的一阶和二阶近似

张启迪

摘 要：Maclaurin公式是Taylor公式的特殊形式，在中学物理竞赛和自主招生的解题中有着重要的应用。然而，Maclaurin公式在进行近似计算时，有时取一阶近似，有时取二阶近似。本文以两道竞赛题为例，浅谈在应用该公式时，如何对阶数进行取舍。

关键词：Maclaurin公式；一阶近似；二阶近似；物理情景；物理意义

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）10-0028-2

1 引 言

Taylor公式和Maclaurin公式是大学物理学习过程中非常常用的两个公式，而Maclaurin公式是泰勒公式的特殊情况，即在满足Taylor定理的前提下，当泰勒公式中x0=0时，公式成为f（x）=

f（0）+f'（0）x+x2+…+xn+xn+1，（0<θ<1）。

在一定条件下，所有的函数都可以用Maclaurin公式展开，由公式可以看出，展开后分别为x的一次方到n+1次方。在物理学中，很多时候需要近似计算，当x→0时，我们可以略去高阶无穷小量，从而使函数关系变得简单，易于找到其中的物理规律。下面我们通过两道竞赛题来看看如何对阶数进行取舍。

2 Maclaurin公式一阶近似举例

例1 新发现一行星，其星球半径为6400 km，且由通常的水形成的海洋覆盖着它的所有表面，海洋的深度为10 Km。学者们对该行星进行探查时发现，当把试验用的样品进入行星海洋的不同深度时，各处的自由落体加速度以相当高的精确度保持不变。试求此行星表面处的自由落体加速度。已知万有引力常数G=6.67×10-11 N·m2/kg2。

我们知道，质量均匀分布的球壳对中间任意一点的万有引力合力为零，对样品真正有引力作用的应当是内部水球壳和星球。随着样品在水中不断下降，内部水球壳的质量显然在减小，那么样品受到的万有引力一定在减弱，严格来说，样品是不可能以恒定的加速度下落的。题目中也着重强调，“各处的自由落体加速度以相当高的精确度保持不变”，对此的理解应当是自由落体加速度肯定是变化的，但是精度要求不高的时候，近似保持不变。继续翻译成数学语言，重力加速度g应当是关于样品距球体深度的函数，当要求精度不高的时候，应当略去x的高阶小量，而保留x的一阶量，又不随x发生变化，则x前的系数应当为0。

首先，我们将g表示成关于深度x的函数，即

g（x）=（其中M为球体质量，R为6400 km，ρ为水的密度），对上式化简，并略去x的二阶和三阶项得：

g（x）=，又根据二项式定理（1+α）n≈1+nx（其中0<α<<1），得：

g（x）=（1+）（1-）=

1+（-）x（其中，=<<1，且已略去x的二阶项）。

要求在相当精确度下，自由落体加速度不随x变化，则x前的系数必为0。即

-=0，化简可得g≈=2πGρR。

依照题意，在相当高的精度下，我们并不关心g（x）函数的整体面貌，而仅仅关心x∈（0，10） km这样一个小范围内g（x）函数的形态。所以，我们应当舍去高阶小量，仅保留一次项。本题中应当注意题目中创设的情景，针对所要研究的问题，进行相关近似。那么，在研究物理问题，需要用Maclaurin公式做近似的时候，是不是一般都进行一阶近似呢？我们继续看下一个例题。

3 Maclaurin公式的二阶近似举例

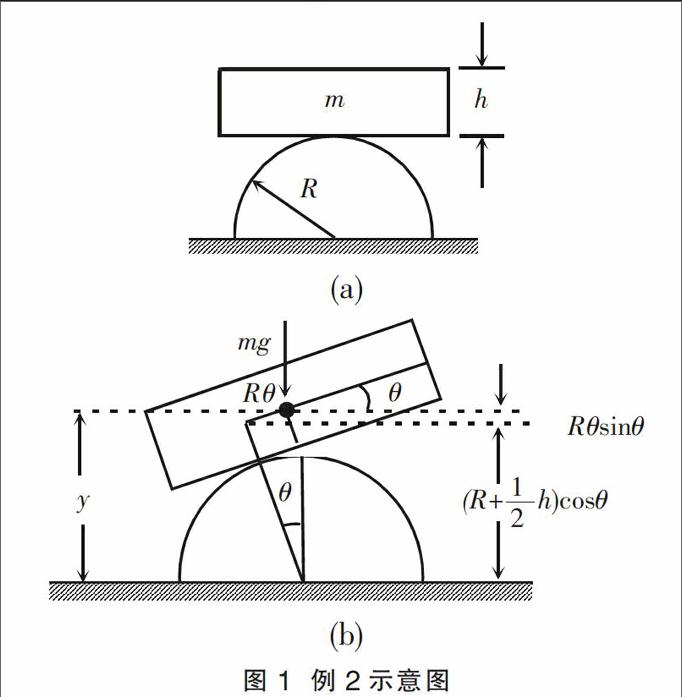
例2 一块厚度为h的匀质长方形物块，静止地放在半径为R的半圆柱顶面上，如图1所示。设摩擦系数足够大，长方形物块与柱面不发生滑动。求此静止位置为稳定平衡的条件。当θ很小时，有关系：cosθ≈1-，sinθ≈θ。

（a）

（b）

图1 例2示意图

物体平衡位置为稳定平衡位置的条件是：当此物体稍微偏离平衡位置时，将受到指向平衡位置的合力作用（平衡力），使物体回到平衡位置。换句话说，如果物体向两侧移动一个微小的距离，物体的重心提高了，即重力势能增加了，则物体将在重力的作用下回复到平衡位置，为稳定平衡，若重力势能减小则不是稳定平衡。以此为以下计算的依据可得：

设长方形物体稍微离开平衡位置，如图1（b），当θ很小，重心位置（离地面）R+，

y=（R+）cosθ+Rθsinθ≈（R+）（1-）+Rθ2=

（R+）-（R+）+Rθ2=（R+）+（R-），稳定平衡的条件为y-（R+）>0，即（R-）>0，解得稳定平衡条件为R>。

从上边的解题过程中，我们可以看出，在做小角度近似时，将cosθ≈1-，sinθ≈θ，题目中给出了这个条件，但是为什么cosθ中含有小角度的二阶项，而sinθ中仅有小角度的一阶项呢？

我们先用Maclaurin公式对正弦函数和余弦函数展开，若用能量观点去解决稳定平衡问题，重力势能必须表达成关于θ2的函数，这是为什么呢？我们先来看下，在此情境中，重力势能和回复力之间的关系。因为ΔEP=-FΔx，则F=-，即回复力应当是势能相对于其自变量的梯度。我们知道，物体若为稳定平衡，则必定受到一个回复力，即势能的表达式对自变量的梯度，必须正比于自变量。在此题中，重心的纵坐标正比于ΔEP，而当θ很小的时候，ΔEP的自变量就是θ。根据以上分析可得，∝θ才能满足回复力的关系。观察表达式y=（R+）cosθ+Rθsinθ，只有对cosθ展开时保留二阶项，对sinθ展开时保留一阶项（sinθ前方有θ一阶存在），才能保证∝θ，这样能量的表达式才能满足其对自变量的梯度为正比于力这样的物理意义，形成稳定平衡的体系。本题也可以通过力矩的观点来研究，此时利用Maclaurin公式展开，需要利用sinθ≈θ，cosθ=1的近似，这里不再赘述，请参阅参考文献。

4 结 语

本文通过两个例子，浅谈了利用Maclaurin公式进行数值近似时，要根据题目中特定的物理情景，考虑到实际的物理意义，恰当地选择一阶或者二阶近似。我们在日常教学中应当广泛关注数学与物理结合的问题，这样才能帮助学生们在早期养成良好的数理素养。

参考文献：

[1]程稼夫.中学奥林匹克竞赛物理教程·力学篇[M].合肥：中国科学技术大学出版社，2012.

（栏目编辑 李富强）