不平顺谱对列车轨道系统动力性能影响的对比分析

张重王(越南)，刘学毅，苏成光，赵 林

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

不平顺谱对列车轨道系统动力性能影响的对比分析

张重王(越南)，刘学毅，苏成光，赵 林

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

轨道不平顺是影响高速列车-轨道系统动力响应的主要因素之一，为了对比分析不平顺谱对列车轨道系统的影响，运用轮轨系统动力学的基本原理，建立列车-无砟轨道-路基系统垂向耦合动力模型，计算分析3种不平顺谱下车辆和轨道系统的动力响应。结果表明：不同轨道谱作用下车辆与轨道系统动力响应具有较大的差异，美国轨道谱的影响最大；武广客运专线轨道谱的影响最小，但对轨道系统的影响与德国谱相近。建议对于具体实际问题，应选用合理轨道谱：既有的武广客运专线不平顺谱是在运营初期测得，适用于开通初期的高速铁路线路，对于已经运营数年的武广客运专线，应进行不平顺谱的复测，才能准确反映实际情况。

轨道不平顺；动力响应；轨道系统；高速列车；

高速铁路无砟轨道必须要保持高平顺性，否则会影响高速行车的安全性和舒适性。轨道结构的几何状态受钢轨伤损、轨枕间距、轨道板钢筋级配、扣件间距与刚度(或阻尼)、路基下沉等众多因素的影响[1]，会造成轨道不平顺的随机特征。轨道不平顺是列车-轨道系统的动力响应的主要影响因素，轨道受随机不平顺激扰时，车辆与轨道耦合系统会产生随机振动，影响到车辆与轨道系统的受力和变形。

目前，世界上有多个国家都对轨道不平顺进行了研究，并建立了相应的密度函数。其中，中国、德国和美国等对轨道谱经过多年研究，理论和实验都较为成熟。研究表明，在进行动态分析时，采用不同的轨道不平顺谱时，车辆、轮轨与轨道结构系统动力的响应都具有较大的差异。在计算模型中，主要对比分析美国、德国、武广客运专线不平顺谱对车辆及轨道系统的动力影响。因车辆与轨道是一个相互作用、相互影响的耦合动力系统[2-4，9]，对列车在不同轨道谱条件下的动力特性进行研究，应将列车与轨道考虑为一个耦合系统。

以CRTSⅠ型板式无砟轨道为例，将路基上单元板式无砟轨道与列车作为研究对象[5]，利用轮轨系统耦合动力学理论及有限元方法，建立列车-轨道系统垂向耦合空间模型，并借助有限元软件ANSYS/LS-DYNA[6-7]，分析不同的轨道谱对高速列车的振动特性、轮轨相互作用及轨道动力的影响，同时对不平顺谱给出了合理的评价。

1 列车-无砟轨道-路基耦合振动模型与求解方法

由于本文只考虑不同高低不平顺谱对列车与结构系统动力的响应，因此，对车辆-无砟轨道做相应的简化，只考虑车辆、轨道和路基的垂向振动。通过ANSYS/LS-DYNA软件进行模型求解[6-7]，针对CRTSⅠ型板式轨道，建立了如图1所示的车辆-无砟轨道系统垂向耦合动力模型[8-9]。车辆采用CRH2动车，视为多刚体系统，车体和构架考虑浮沉、侧滚和点头3个自由度，轮对考虑浮沉和侧滚两个自由度，因此整个车辆模型中共有17个自由度；一系、二系悬挂简化为弹簧阻尼元件，其参数取值参照文献[8]。轮轨接触按照赫兹接触理论计算并简化为线性弹簧，刚度取1 490 MN/m。模型总长度为100 m，钢轨采用CHN60钢轨，视为间断点支承梁；扣件为WJ-7扣件，简化为弹簧阻尼元件，扣件刚度和阻尼分别取50 kN/mm和75 kN·s/m；轨道板尺寸为4.95 m×2.4 m×0.19 m、底座板尺寸为3.2 m×0.3 m(分段连续)均简化为弹性薄板；砂浆层与路基层均简化为均布弹簧，其弹簧刚度按砂浆弹性模量300 MPa，路基刚度按支承面刚度120 MPa/m计算得到。

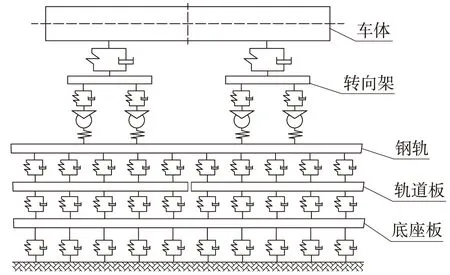
图1 列车-轨道-路基垂向耦合振动模型

采用有限元方法按每个扣件间距划分单元对轨道板和底座板进行离散，得到轨道结构系统在t时刻的动力响应方程为

(1)

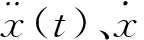
模型中，通过LS-DYNA[4，5]的显示动力分析程序，采用中心差分法。计算结构系统在第n个时间步结束时刻tn的加速度向量通过公式(2)进行计算，即

(2)

式中，F(tn)为第n个时间步结束tn时刻施加的节点外力向量；Fint(tn)为第n个时间步结束tn时刻的内力向量，包含当前tn时刻单元应力场等效节点力、沙漏阻力以及接触向量[4-5]。

按中心差分法的基本思路，其节点的速度向量v与位移向量u通过公式(3)和(4)进行计算

(3)

(4)

式(3)和式(4)中，时间步与时间步开始的定义，即

(5)

(6)

新的结构变形由初始结构变形x0加上位移增量u得到，即

(7)

2 轨道谱的选取及模型验证

为了对比不同的轨道谱对车辆与轨道系统的动力影响。在计算中，本文选取美国、德国、武广客运专线不平顺来进行对比分析。德国高低不平顺谱采用低干扰谱，美国高低不平顺谱采用六级轨道谱，德国与美国不平顺谱如图2、图3所示，为根据文献[10]中方法得到的时域随机不平顺样本。

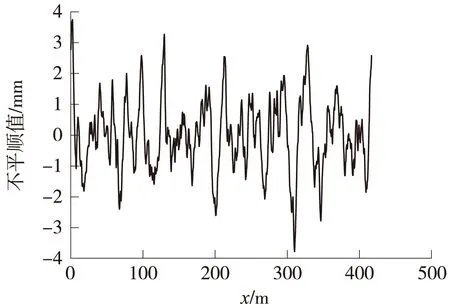
图2 德国随机不平顺谱的样本

图3 美国随机不平顺谱的样本

2009年，中国铁道科学研究院提出利用轨道不平顺中位数谱表示轨道不平顺谱的方法，其提出的客运专线轨道不平顺谱及公式为

(8)

式中，A为轨道不平顺粗糙度常数；f为不平顺空间频率；f0，f1分别为轨道不平顺侧、断面频率，单位为m-1；k1、k2、k2为待定系数，其按武广客运专线轨道不平顺谱参数来取值。此外，本文根据功率谱求出频谱的幅值与随机相位，然后通过傅立叶逆变换(IFFT)转换得到的随机不平顺数据见图4。

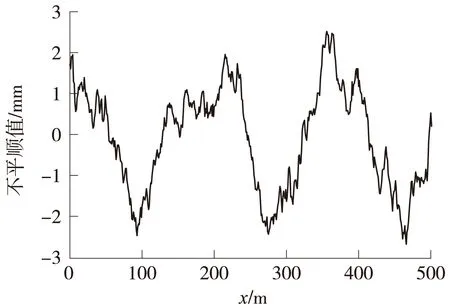
图4 武广客运专线随机不平顺谱的样本

为验证所建立的列车-轨道-路基垂向耦合动力模型的正确性与可靠性，将模型仿真计算结果与实测值[11-12]进行对比。按行车速度为300 km/h，采用德国轨道谱时，进行动力响应分析计算，仿真计算与实测的结果如表1所示。可以看出，由于实测现场条件和仿真模型环境不尽相同，所以实测和仿真结果存在一定差异，但从总体来看，计算结果与测试值基本一致，表明所建立的动力学模型较可靠。

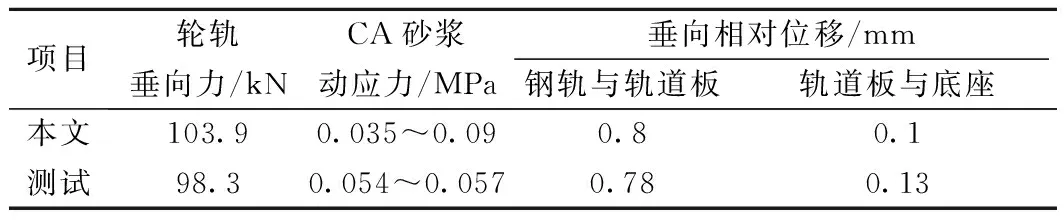
表1 仿真结果与动力实测值对比

3 计算结果及对比分析

为计算分析车辆与轨道系统动力特性，对比分析行车速度为300 km/h在不同轨道不平顺谱的条件下轮轨系统各部件的加速度、垂向力、位移等动力特性。

3.1 车辆动力特性及轮轨力

图5～图8分别为不同轨道谱条件下，轮轨垂向力和车体、转向架、车轮垂向加速度响应变化的曲线。车辆系统各部件动力响应最大值如表2所列。

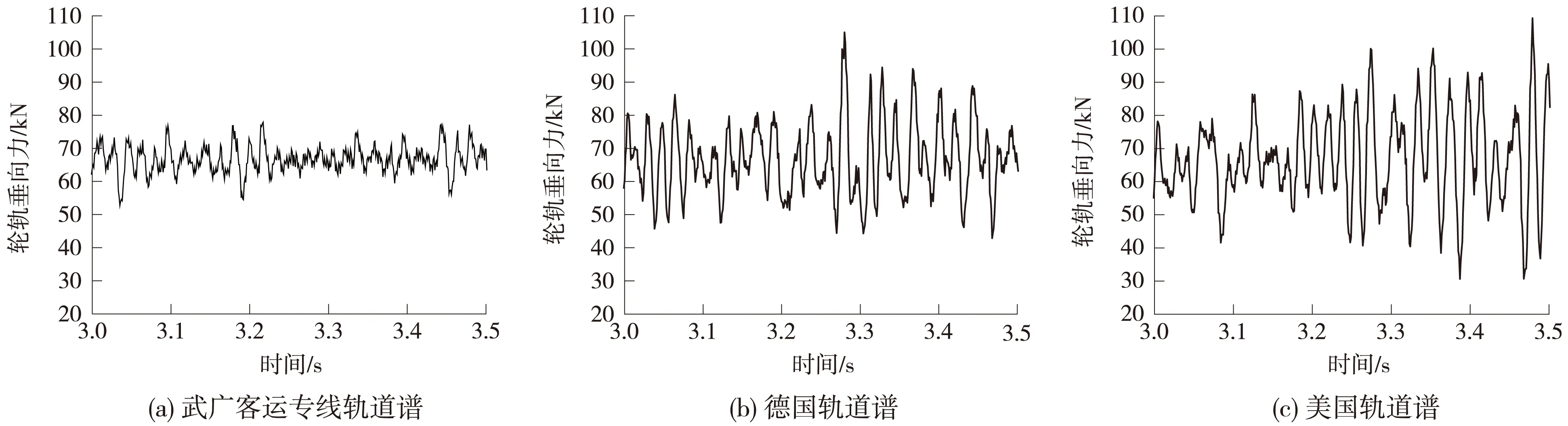
图5 轮轨垂向力的时程对比

图6 车体垂向加速度时程对比

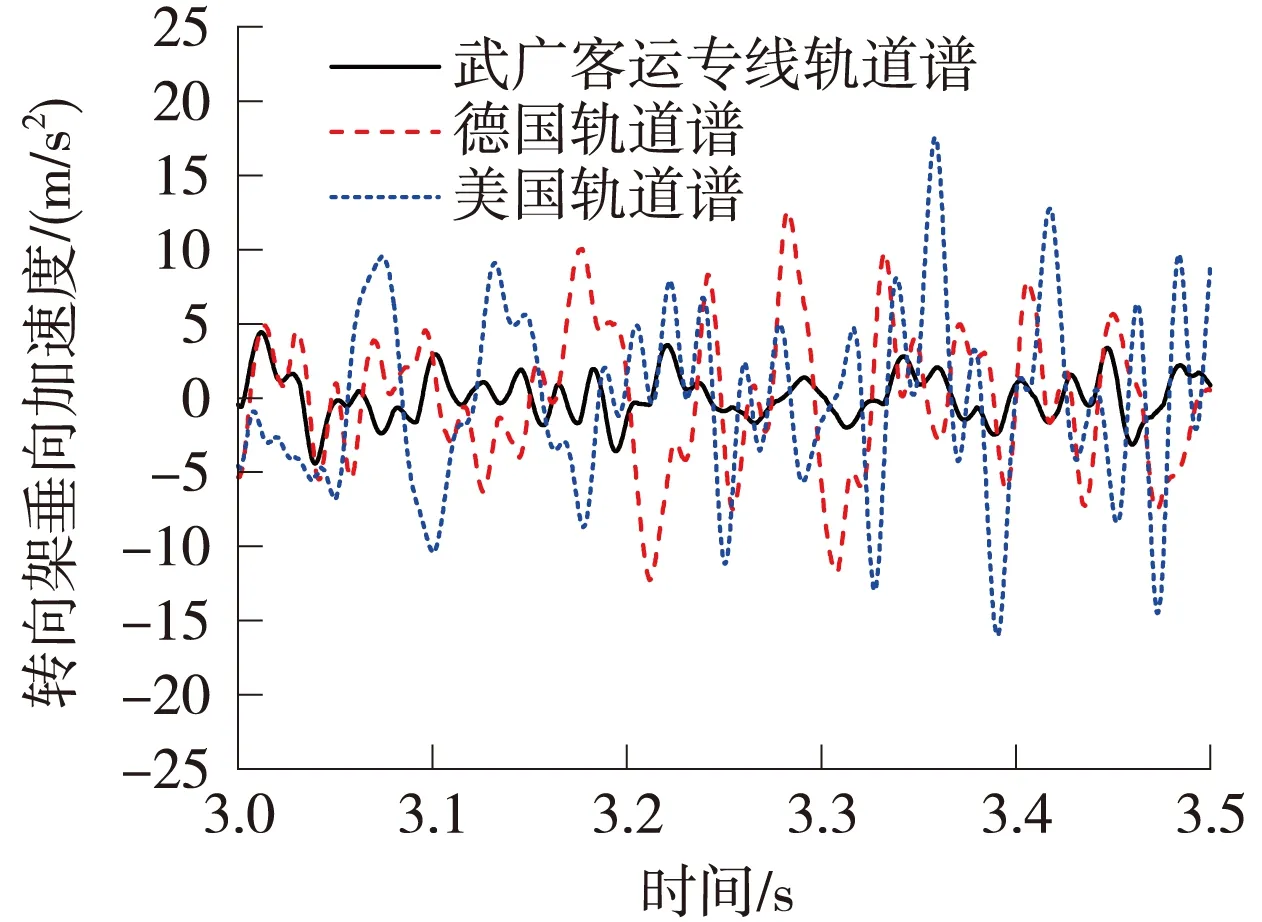
图7 转向架垂向加速度时程对比

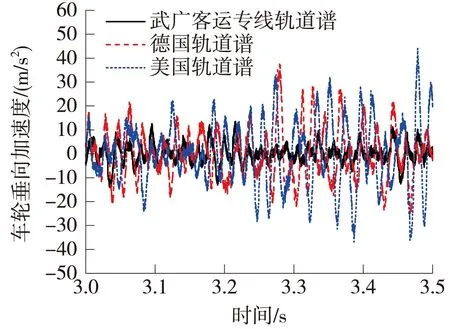
图8 车轮垂向加速度时程对比

由图5可知，在轨道所受不同随机不平顺激扰时，轮轨垂向动力的响应具有较大的差异。美国轨道谱对轮轨垂向力影响最大，最大值为109.3 kN，小于允许限值170 kN，分别比德国、武广客运专线轨道谱大5.4、31.42 kN；美国、德国与武广客运专线轮轨垂向力最小值分别为30.66、40.92、52.78 kN；减载率分别为0.55、0.4、0.23。

由图6可知，在不同轨道谱条件下，车体垂向加速度变化较大。美国轨道谱对车体垂向加速度影响最大，最大值为0.92；较德国、武广客运专线轨道谱分别增大33%和268%。

由图7和图8可知，在不同轨道谱条件下，转向架与车轮垂向加速度动力的响应存在较大的差异。其中，武广客运专线不平顺谱对转向架与车轮垂向加速度影响最小，美国不平顺谱对转向架与车轮垂向加速度影响最大；美国不平顺谱、德国不平顺谱与武广客运专线不平顺谱的转向架和车轮垂向加速度分别为17.55、12.63、4.43 m/s2和44.11、37.55、14.06 m/s2。

从表2可以看出，武广客运专线不平顺谱对车辆动力响应影响最小，美国不平顺谱对车辆动力响应影响最大；总体来看，武广客运专线不平顺谱对车辆动力响应影响远小于德国与美国不平顺谱。

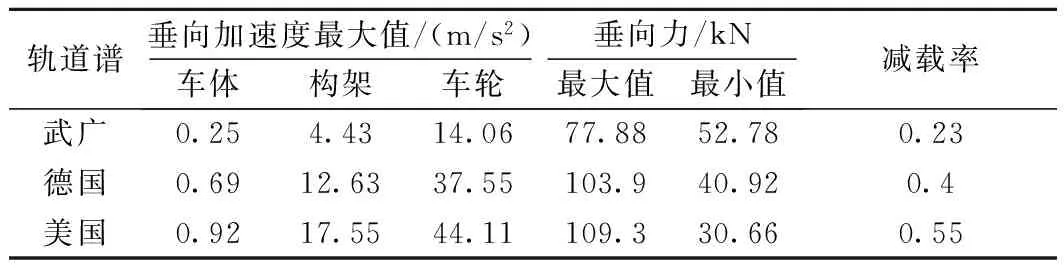
表2 不同轨道谱时系统各部件动力响应对比

3.2 轨道动力特性

在不同不平顺谱条件下，行车速度为300 km/h时，计算得出如图9～图13及表3所示的结果。由图9可知，武广客运专线和德国不平顺谱下轨道板垂向加速度动力响应相近，最大值分别为27、26.3 m/s2；美国不平顺谱下轨道板垂向加速度动力响应较武广客运专线和德国谱略大，最大值为34.95 m/s2，较武广客运专线、德国谱分别增大29.44%、32.89%。

图9 轨道板垂向加速度的时程对比

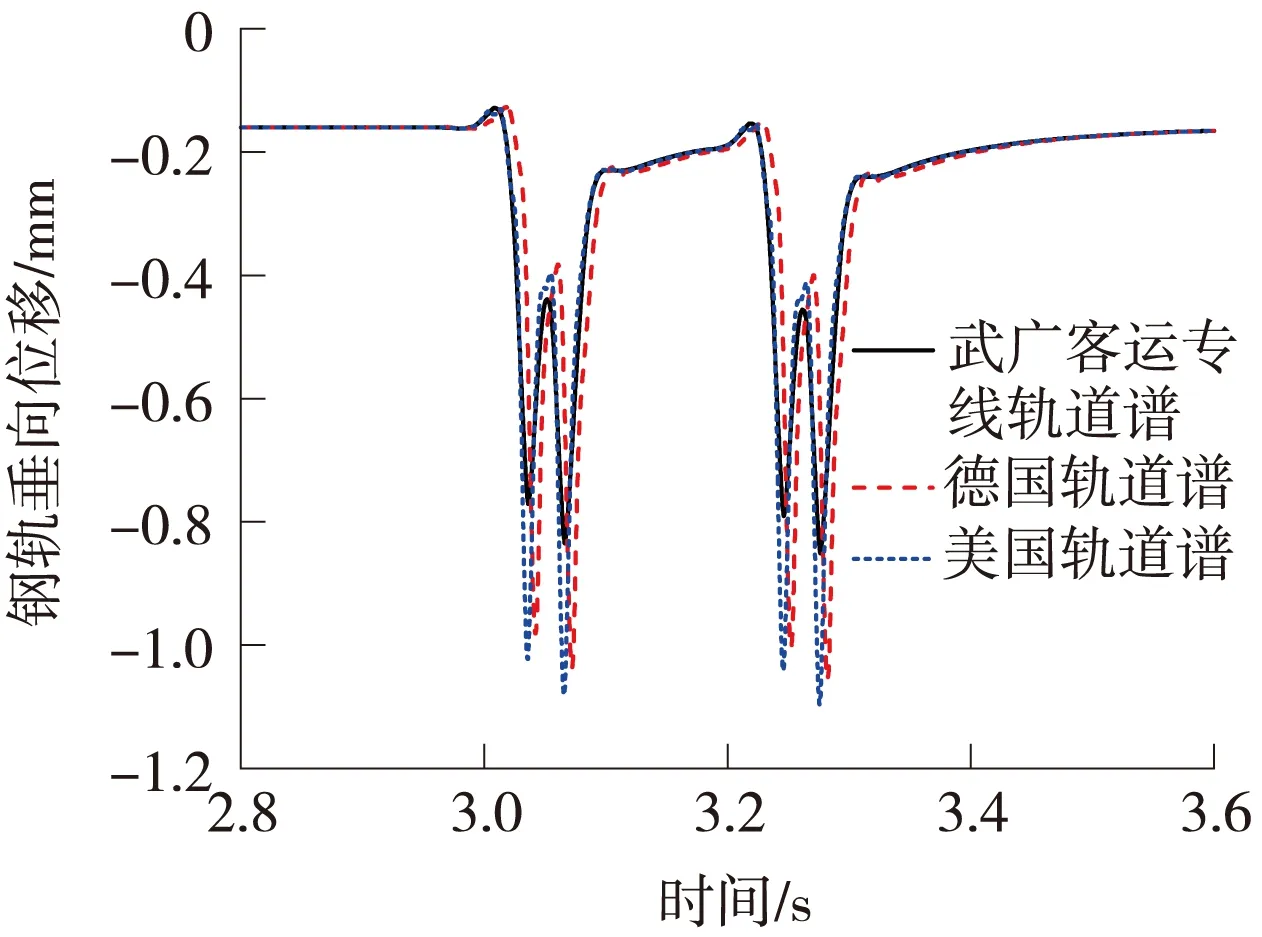
图10 钢轨垂向位移时程对比

图11 轨道板垂向位移时程对比

图12 钢轨支点压力时程对比

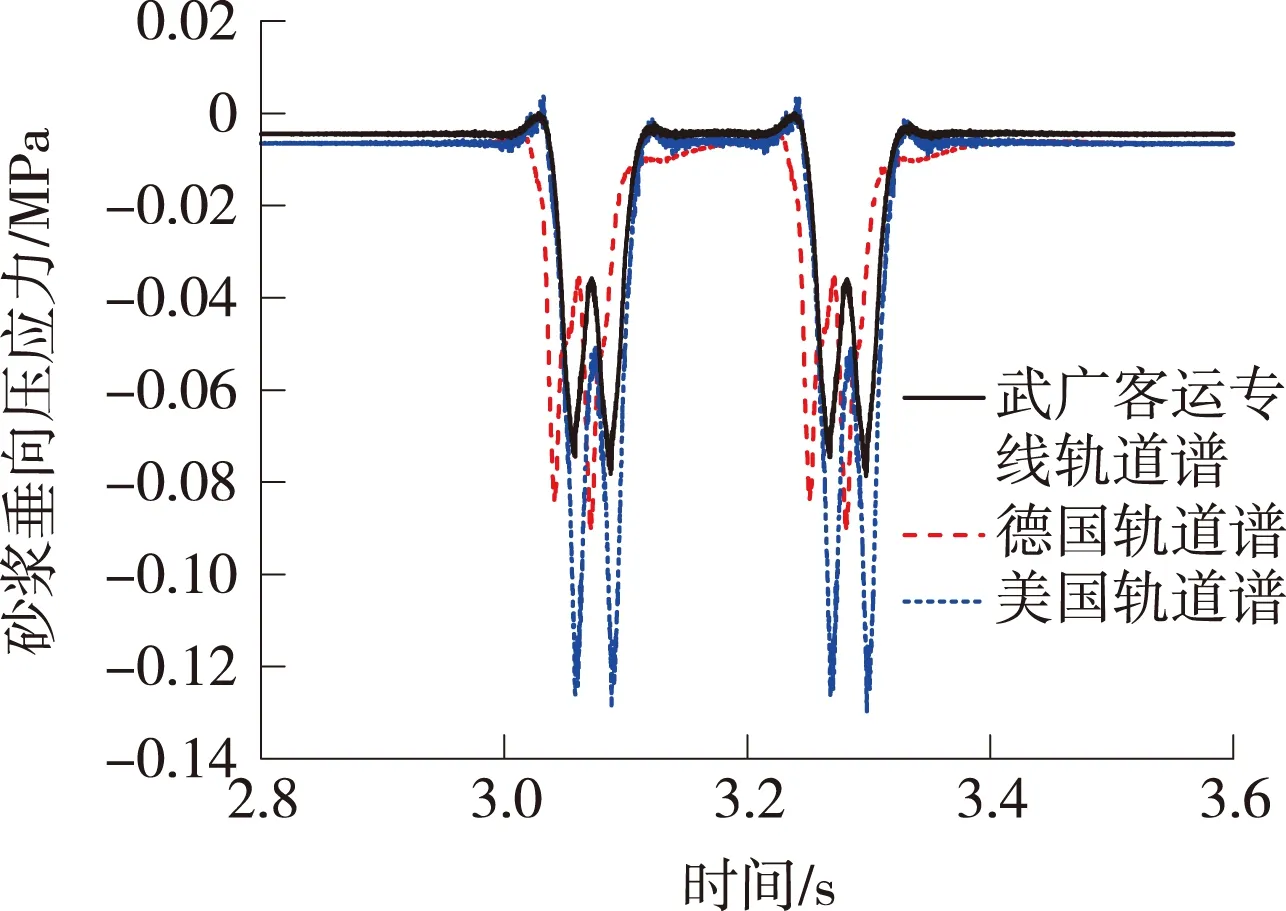
图13 砂浆垂向压应力时程对比

由图10可知，在不同轨道谱条件下，钢轨垂向位移动力的响应具有较明显的差异。美国、德国和武广客运专线不平顺谱下的钢轨垂向位移最大值分别为1.09、1.06、0.85 mm。由图11可知，在不同轨道谱条件下，轨道板垂向位移动力的响应基本一致，最大值都为0.26 mm。

由图12和图13可知，美国轨道谱对钢轨支点压力和砂浆垂向压应力影响最大，分别为32.37 kN和0.13 MPa，较德国和武广客运专线分别增大33.15%、45.15%和44.44%、56.62%。德国和武广客运专线轨道谱对钢轨支点压力和砂浆垂向压应力动力的响应较接近，最大值分别为24.31、22.3 kN和0.09、0.083 MPa。

从表3可以看出，美国轨道谱对轨道系统动力影响较德国和武广客运专线大。武广客运专线与德国不平顺谱对轨道系统各部件动力的响应比较相近。

通过上述分析可知，不同轨道谱对车辆与轨道系统动力的影响具有较明显的差异。武广客运专线不平顺谱对车辆系统动力响应的影响远小于美国和德国谱，但对轨道系统动力响应的影响与德国谱较相近。此外，既有的武广客运专线不平顺谱是在运营初期测得，适用于开通初期的高铁线路，对于已经运营数年的武广客运专线线路，应进行不平顺谱的复测。

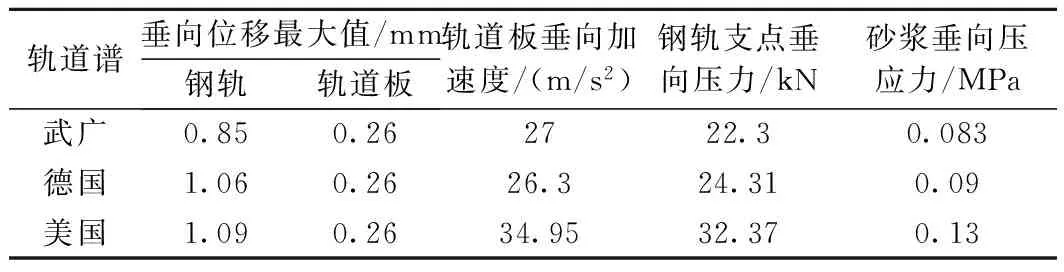
表3 不同轨道谱时轨道系统各部件动力响应对比

4 结论

本文通过研究不平顺谱对列车-轨道系统动力特性的影响，得出了如下结论：

(1)不同轨道谱对车辆与轨道系统动力响应的影响具有显著的差异，美国轨道谱的影响最大；武广客运专线轨道谱的影响最小，但对轨道系统的影响与德国谱相近；

(2)既有的武广客运专线不平顺谱是在运营初期测得，适用于开通初期的高铁线路，对于已经运营数年的武广客运专线线路，应进行不平顺谱的复测，才能反映实际情况。

[1] 刘克飞.框架型板式轨道水泥乳化沥青砂浆伤损及维修标准研究[D].成都：西南交通大学，2013．

[2] 蔡成标.高速铁路列车-线路-桥梁耦合振动理论及应用研究[D].成都：西南交通大学，2004．

[3] 翟婉明，夏禾，等.列车-轨道-桥梁动力相互作用理论与工程应用[M].北京:科学出版社，2011．

[4] 蔡成标，翟婉明，王开云.高速列车与桥上板式轨道动力学仿真分析[J].中国铁道科学，2004，25(5):57-60．

[5] 徐庆元，范浩，李斌.无砟轨道温度梯度荷载对列车-路基上板式无砟轨道系统动力特性的影响[J].铁道科学与工程学报，2013，10(3):1-6.

[6] JOHN O. Hallquist. LS-DANA®theory manual. USA: Livermore Software Technology Livermore，2006．

[7] 李裕春，时党勇，赵远. ANSYS 11.0/LS-DYNA基础理论与工程实践[M]. 北京：中国水利水电出版社，2008:19-80．

[8] 翟婉明.车辆-轨道耦合动力学[M].3版.北京:科学出版社，2007.

[9] 刘学毅，王平.车辆-轨道-路基系统动力学[M].成都:西南交通大学出版社，2010．

[10]张立伟，冯军和.轨道不平顺随机过程的数值模拟[J].世界地震工程，2008，24(1):103-109.

[11]中国铁道科学研究院.武广客运专线武汉综合试验段综合试验研究总报告[R].北京:中国铁道科学研究院，2009．

[12]相颖慧，罗强，魏永幸.遂渝铁路无砟轨道涵洞附近CA砂浆层动应力测试分析[J].铁道工程学报，2008(6):43-47.

Contrastive Analysis of the Influence of Irregularity Spectrum on Train-track System Dynamics Characteristics

TRUONG Trong-vuong， LIU Xue-yi， SU Cheng-guang， ZHAO Lin

(MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China)

Track irregularity is one of the main factors affecting train-track system dynamics response. In order to analyze contrastively the influence of irregularity spectrum on train-track system， train-ballastless track-roadbed system vertical coupling dynamics model is established based on fundamentals of wheel-rail system dynamics， and the influence of irregularity spectrum of different tracks on train-track system dynamics response is analyzed. The results show that train-track system dynamics responses are different remarkably under different track spectrums. American track spectrum has the most impact on train and track system dynamics response， while Wuhan-Guangzhou track spectrum has minimal impact， but its track system dynamics response is similar to that of Germany spectrum. Reasonable track spectrum shall be selected accordingly. The existing Wuhan-Guangzhou irregularity spectrum was tested at the early age of operation and its irregularity spectrum applies only to the initial operation stage of high-speed lines. In view of Wuhan-Guangzhou high-speed rail which has been in service for several years， irregularity spectrum should be retested to reflect accurately actual situations.

Track irregularity; Dynamics response; Track system; High-speed train

2014-10-08；

2014-10-31

国家重点基础研究发展计划(973计划)课题(2013CB036202)

张重王(1977—)，男，越南河内大学讲师，博士研究生，

E-mail:1732697327@qq.com。

1004-2954(2015)07-0015-05

U213.2

A

10.13238/j.issn.1004-2954.2015.07.004